需求不确定下低碳多式联运路径鲁棒优化

邓明君，代玉珍，李响

(华东交通大学 交通运输工程学院，江西 南昌 330013)

根据世界能源统计(BP)数据显示，2021年我国碳排放总额高达119亿t，其中交通运输行业碳排放量约占10.4%。随着“双碳”目标的提出，具有降本增效和节能减排优势的多式联运成为建设新时代绿色低碳交通运输体系重要组成部分，基于此，开展多式联运路径优化研究具有实际指导意义。

综合分析多式联运研究现状可知，已有研究方向主要集中在低碳和不确定。从低碳角度来看，学者们大都采取将碳排放量当成约束条件或将其转化为成本融入目标函数去检验多式联运在低碳环保方面的优势。Lam等[1]在碳排放量约束下构建成本最小化模型。刘学之等[2]、陈维亚等[3]和Laurent等[4]通过将碳排放量转化为碳成本，构建以总成本最小为目标的低碳多式联运路径优化模型，验证多式联运在低碳环保方面的优越性。不确定研究主要表现在对象和处理方法上。陈汨梨等[5]采用随机规划理论估计并验证了不确定的转运时间对路径方案选择的影响程度。Liu等[6]、程兴群等[7]利用区间数来刻画多式联运网络的不确定时间。Ghavami[8]运用模糊理论处理不确定时间。Ávila-Torre等[9]运用模糊规划理论处理不确定的需求。万杰等[10]证实针对不同需求的商品运输，多式联运具有良好的适应性。张旭等[11]提出需求与碳交易价格双重不确定的多式联运路径优化模型。此外，还有学者[12-13]从时间窗和班期角度研究各自对运输决策的作用效果。

根据上述研究现状不难发现，低碳运输是保证多式联运长远发展的必然趋势，而不确定性已成为多式联运路径优化研究的热点与难点。对多式联运不确定性的研究主要侧重在需求量上，对多式联运时效性的研究主要侧重在收货时间窗上，货运需求量的波动会导致运输成本和时间消耗产生连锁效应，进而影响运输方案的选取。结合多式联运实际运输现状，在中转节点考量铁路、水路的班期问题对多式联运的时效性检验必不可少，然而在需求不确定下综合考虑班期和收货时间窗的研究较少，并且现有研究成果在处理不确定性问题大都采用随机理论、模糊理论或区间数。当考虑班期后，采用上述方法处理不确定参数非常困难[14]，而鲁棒优化方法[15]不仅可以在参数波动情况下给出可行性和目标水平相对较好的鲁棒运输方案，还会保证系统的稳定性。

因此本文以多式联运经营人为研究视角，在碳交易政策和需求不确定情景下，考虑班期和收货时间窗对经济成本和运营时间的影响，创建需求不确定下多式联运路径鲁棒优化模型，使用遗传算法来检验优化模型的可行性，使多式联运经营人在面对动态化市场时能高效整合各承运人的运输资源，且兼顾自身的经济效益和环保义务，为客户提供最佳的运输服务，最终实现多式联运服务网络各参与方的共赢。

1 模型创建

1.1 问题阐述

在包含公路、铁路、水路3种运输方式的多式联运运输网络里，某经营多式联运服务的货运代理企业需在客户规定的收货时间内将货物从起点运送至终点。考虑铁路局和港口的实际作业情况，铁路、水路运输有固定的发车班期，而公路运输则无班期约束，固定班期对运营时间的影响如图1所示。考虑到多式联运运输方案制定的超前性以及客户货运量需求的个性化，企业需要在需求不确定的情况下提前拟定出货物运输方案。本文旨在碳交易市场作用下综合评估需求不确定对经济成本和碳排放量造成的影响，建立多式联运鲁棒优化模型，为企业如何制定出价廉高效、低碳环保、稳定可靠的运输方案提供理论方案参考。

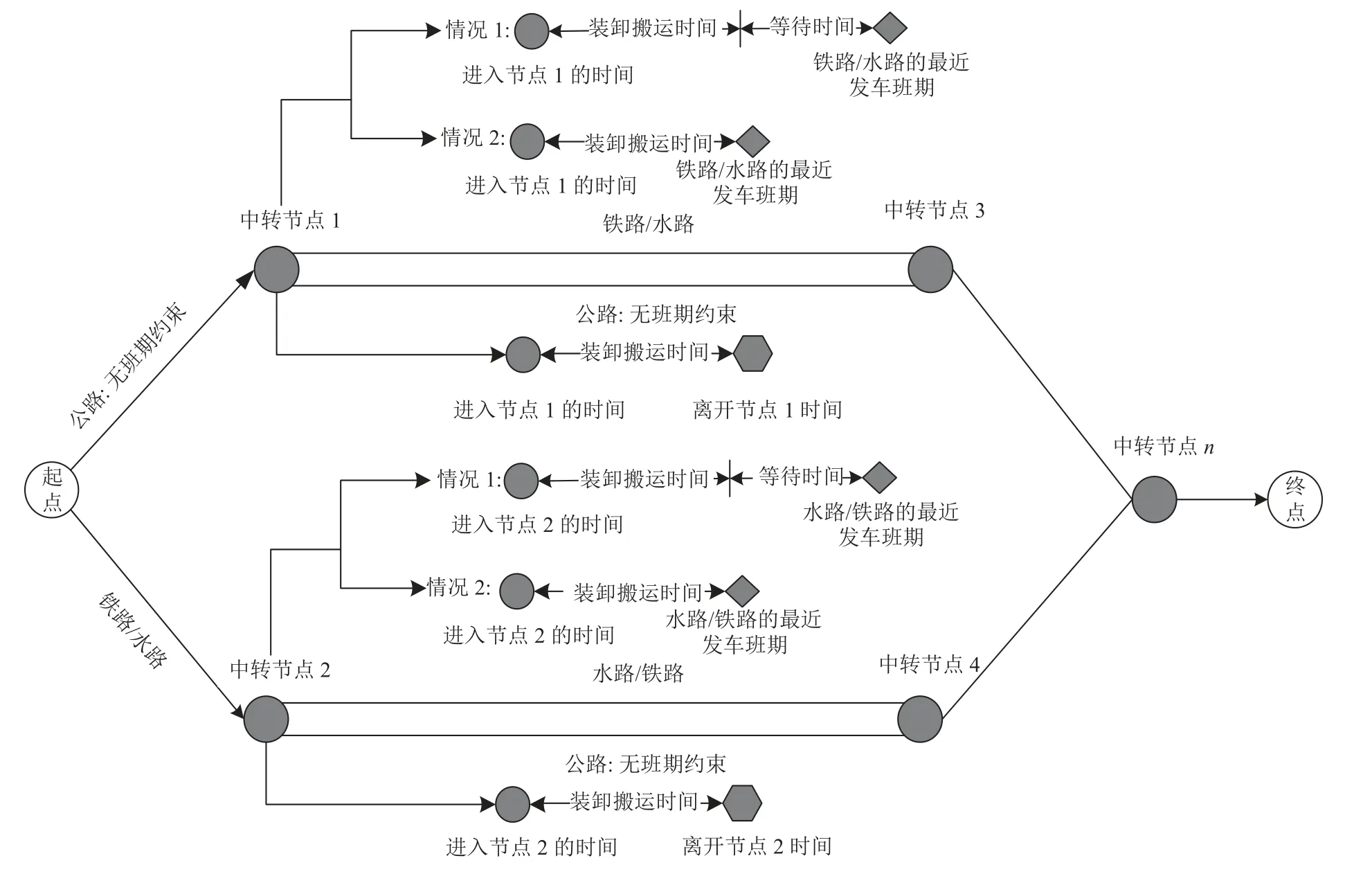
图1 货物在中转节点的时间示意图Figure 1 Time diagram of goods at transit nodes

由图1可知，货物从起点出发到达中转节点，若发生运输方式转换则会产生装卸搬运时间。若以公路运输离开中转节点，则在完成装卸搬运后则可以立即出发前往下一中转节点；若以铁路或者水路运输离开中转节点，则在完成装卸搬运后需等待铁路或者水路运输最近的班期发班时刻来临后才可以出发前往下一中转节点。等待时间即为铁路、水路最近的班期发班时刻与货物完成装卸搬运后时刻的差值。

研究假设如下。

1) 中转只发生在中转节点，且中转最多发生一次；

2) 同一批货物运输过程中不分割；

3) 各运输路径的货运量均小于等于该路径的承载能力；

4) 班期只作用于中转节点；

5) 不考虑货损货差、恶劣天气、设备障碍等原因对运输状况的影响。

1.2 模型建立

1.2.1 参数说明

1) 集合及常量。

N：节点城市集合；

A：运输路径集合；

M：运输方式集合；

h,i,j：运输节点，h,i,j∈N；

(h,i)：运输路径，(h,i)∈A；

k,l,m：分别代表公路、铁路、水路3种货物运输方式，k,l,m ∈M；

C、T、q、Eactual、Eallow：经济成本、运营时间、货物运输总量、碳排放总量、碳排放配额；

C1、C2、C3、C4、C5：在途运输成本、中 转成本、等待成本、仓储/等待成本、碳交易成本；

[TB,TF]：多式联运的收货时间窗；

cb/ (元 ·h-1·t-1) ：在TB前到达终点的单位仓储成本；

cf/ (元 ·h-1·t-1) ：在TF后到达终点的单位惩罚成本；

cg/ (元 ·h-1·t-1) ：在中转节点运输方式转换为l或m时，等待发车的单位等待成本，

ej：单位碳排放配额交易价格，取10元/ kg；

Z：货物的不同需求量情景集合，s∈Z；

qs：情景s下不确定需求量；

ps：情景s发生的概率；

Cs(x)：情景s目标函数的可行解；

Cs∗：情景s下确定性问题目标函数的最优解，设Cs∗＞0恒成立；

β ：情景s下允许的最大遗憾值。当 β=0时，需求是确定的。

2) 决策变量。

1.2.2 需求确定下多式联运路径优化模型

鲁棒优化在求解参数不确定问题时具有较强的抗干扰能力，可保持系统的稳定性，故本文采用鲁棒优化处理引入班期后的需求不确定下多式联运路径优化问题。需基于碳交易政策作用机理，企业拥有一定量的排放额度，完成某减排项目后可根据自己的实际排放量在碳交易市场购买或者出售排放额度，将碳交易成本或收益归入企业的运营成本，建立需求确定下多式联运路径优化模型。故目标函数如式 (1)～ (9) 所示。

其中，式(1) 为在途运输成本；式 (2) 为中转成本；式 (3) 为在中转节点运输方式发生改变产生的等待成本；式 (4) 为过早/过迟交付货物产生的仓储成本/惩罚成本；式 (5) 为在碳交易政策下实际碳排放量小于碳排放配额的碳交易收益或实际碳排放量大于碳排放配额的碳交易成本；式 (6) 为等待时间，分为两种情况：1) 等待时间为0即货物到达i后，完成运输方式由k转换成l的装卸搬运等中转作业后的时间刚好等于发车时刻；2) 等待时间不为0即货物到达i后，完成运输方式由k转换成l的装卸搬运等中转作业后的时间小于最近的发车时刻；式(7) 为在途时间；式 (8) 为运营时间，由在途时间、中转时间、中转节点等待时间3个部分组成；式 (9)为目标函数即经济成本，由在途运输成本、中转成本、在中转节点运输方式发生改变产生的等待成本、过早/过迟交付货物产生的仓储成本/惩罚成本和碳交易成本/收益5个部分组成。

约束条件为

其中，约束 (10) 表示节点的货物流量守恒；约束 (11) 表示货物运输在一条运输路径上只能采用1种运输方式；约束 (12) 表示在一个节点上进行货物中转至多发生1次；约束 (13) 保证各节点前后运输路段的运输方式信息与节点转换信息具有一致性。

1.2.3 需求不确定下多式联运路径鲁棒优化模型

使用鲁棒优化中情景集来表征货物需求量的波动，不用依据主观经验来描述货物需求量分布的数值特征。采用离散或连续情景集合来描述货物需求量的各种情景，构造不确定的需求量，并具有任一情景下的目标函数值与相应的最优目标函数值之间应满足最大遗憾值的鲁棒约束。这使得模型在求解时具有良好的优化效果，增加系统的稳定性。在此基础上，假设货物需求情景集合为Z，每个情景s下不确定需求量为qs，情景s发生的概率ps，将含有变量的原路径优化模型中目标函数转换成鲁棒对等式，创建需求不确定下多式联运路径鲁棒优化模型。目标函数为

约束条件为

式(10)～ (13) 同时成立。

其中，式(14) 为基于不确定需求情景的多式联运路径鲁棒优化的目标函数；式 (15) 为关于目标函数解的鲁棒约束，表示任一情景下可行解的目标函数与最优目标函数的相对遗憾值要小于 β；式 (16)表示所有情景发生的概率之和为1。

2 求解算法

在碳交易政策下，考虑班期和收货时间窗的双重约束，研究需求不确定的多式联运路径鲁棒优化问题，通过模拟推演多式联运运输全过程，构建需求不确定下多式联运路径鲁棒优化的模型中涉及众多的中间变量，结构复杂。但遗传算法[16]是一种有效的解决最优化问题的方法，它吸收了自然生物系统“适者生存”的进化原理，使得它能提供在复杂空间中进行鲁棒搜索的方法，与研究问题自身特点相契合，故采用遗传算法对模型进行求解。算法流程图如图2所示，算法主要包括以下6个步骤。

图2 遗传算法流程图Figure 2 Flowchart of genetic algorithm

步骤1染色体编码。

由于多式联运运输方案的选择包括运输节点和运输方式，并且起讫点之间运输方案是随机生成，故采用可变长的运输方案编码方式，随机生成一条运输方案如图3所示。

图3 编码示意图Figure 3 Schematic diagram of encoding

步骤2生成初始种群。

由于研究多式联运运输网络图是单OD，即从起点出发，随机选择运输方式，根据不同的运输方式的稀疏矩阵，寻找下一个中转节点，循环下去直至到达终点，则得到一条初始染色体；若染色体数量达到种群规模，则终止。

步骤3选择。

遗传选择采用轮盘赌选择。因本文中以经济成本最小为目标，遗传算法的适应度值越大越好，故适应值函数为目标函数的倒数，即f=1/C。

步骤4交叉。

采用单点交叉，即交叉选取在OD之间的中转节点上，且仅当配对的两个父代染色体存在相同的中转节点时，才进行交叉，如不存在相同的中转节点就不进行交叉。交叉发生的情况如图4所示。

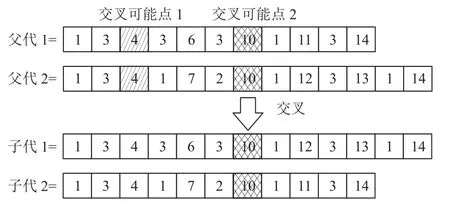
图4 交叉过程图Figure 4 Diagram of a cross process

步骤5变异。

在交叉后产生的新染色体上随机选择除OD外的基因进行变异操作。若变异发生在偶数基因上，则进行运输方式的变异，若发生在奇数基因上，则进行中转节点的变异。变异位的可能情况如图5所示。

图5 染色体变异示意图Figure 5 Diagram of chromosome mutatim

步骤6移民算子。

引入移民算子旨在避免求解时陷入过早收敛和搜索迟缓，故在按适应度排序后以16%的淘汰率滤除低劣个体，用适应度排名前16%的父代个体进行若干次交叉、变异产生新的个体去替代被滤除的低劣个体。这样既保留了父代的优秀基因，又增加了基因的多样性，动态解决了过早收敛与搜索迟缓的问题。

3 算例验证

3.1 参数设置

某经营多式联运服务的货运代理企业现需将一批需求不确定的货物从起点“1”运送到终点“14”，且货物需要在收货时间窗[50,60] h内到达终点，但若提前到达终点则会产生8元/(h·t)的单位仓储费用，若延迟到达则会产生20元/(h ·t)的单位惩罚成本。铁、水路班期产生的单位等待成本为8元/(h·t)，多式联运运输网络图如图6所示。

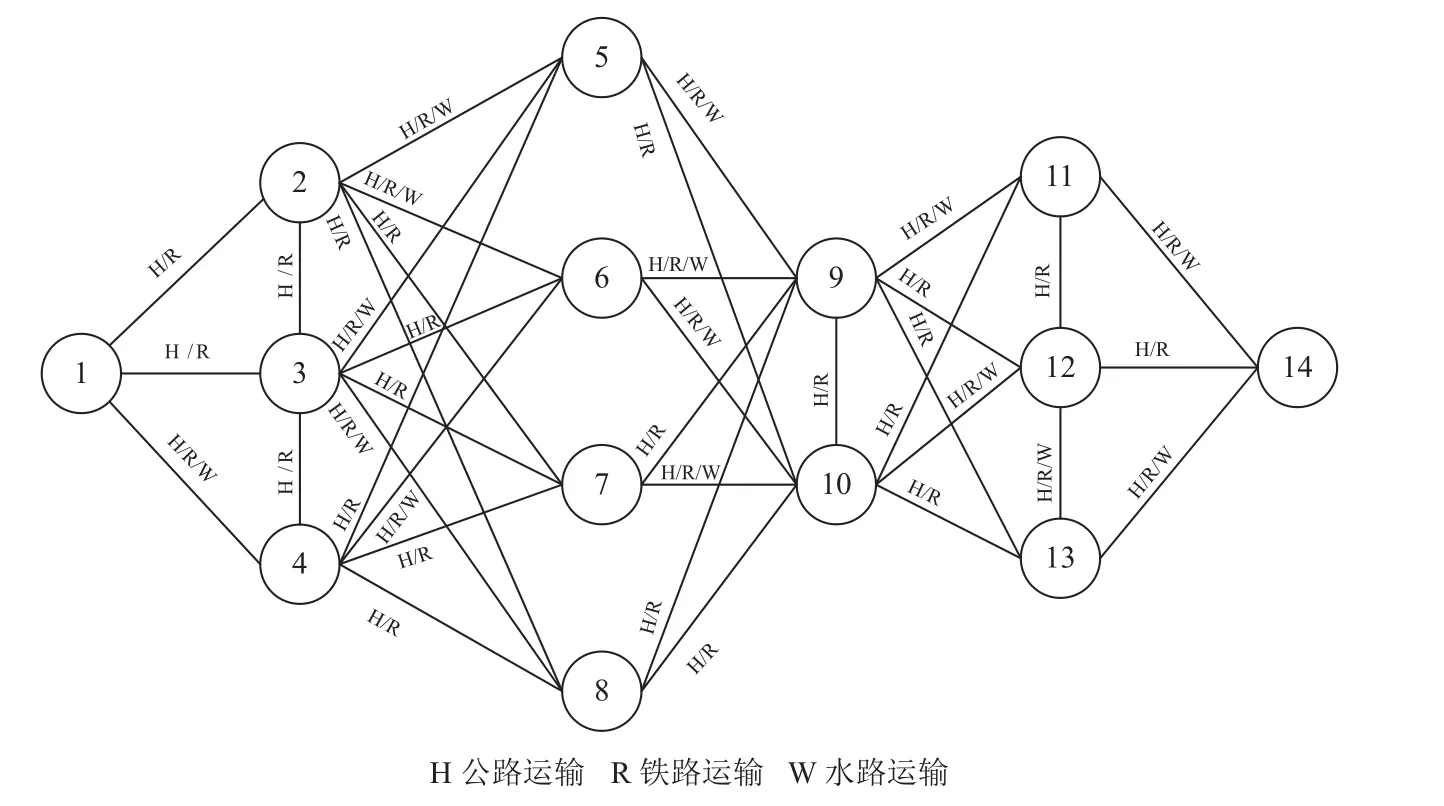
图6 多式联运运输网络图Figure 6 A multi-modal transportation network

图6中各运输路径的不同运输方式对应的运输距离见表1所示，其中“—”表示两节点间的运输路径不存在某种运输方式。

表1 各节点间不同运输方式的运输距离Table 1 Distance of different transportation modes between each two nodes

根据相关的文献资料[11]，并参照各运输企业的实际情况，得到各运输方式的运输参数，见表2。其中，各运输方式的单位碳排放量采用《2006年IPCC指南》中提供的碳排放因子法由对应能源的消耗量及能源的CO2排放系数估算所得，单位运价中(a,b,c) 分别表示各运输路径间运输距离在[0,500]、(500,1 000]、(1 000,+∞) 3个区间范围里的单位货物运输成本。

表2 3种运输方式的运输参数Table 2 Parameters of three transportation modes

通过查询相关文献资料[6]与各货运中转站的具体情况，得到各运输方式的中转参数，见表3。

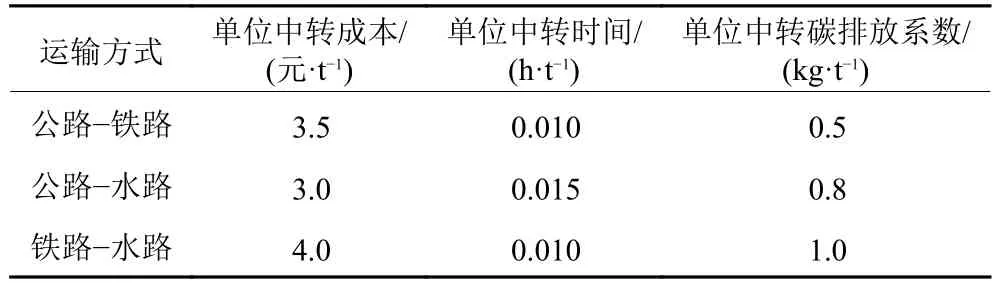
表3 各运输方式的中转参数Table 3 Transferring parameters of each transportation mode

考虑到铁路、水路在实际运输过程中均存在班期限制，参考相关文献资料[13]，得到各运输方式的发车时刻表，见表4。

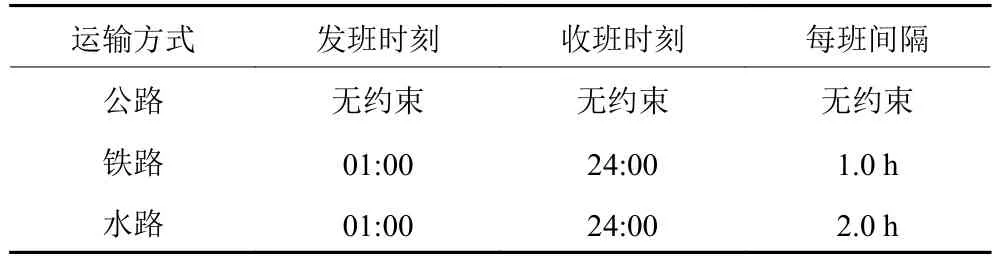
表4 各运输方式的发车时刻表Table 4 Departure time of each transportation mode

由于运输计划具有超前性，客户的需求量无法确定。根据现实中货运量的分布特征以及相关文献中的设计[17]，假设低货运量、中货运量、高货运量情景下的货运量均服从正态分布，均值与方差分别为q～N(125,69.4)、(175,69.4)、(225,69.4)，低货运量、中货运量、高货运量情景的概率ps分别为0.36、0.5、0.14。此外，不同情景下的碳排放配额分别为3 000 kg、4 000 kg、5 000 kg。

3.2 算例分析

根据所建立模型，最大遗憾值β=0.2，采用遗传算法，利用Matlab R2019a程序编程，将算法的参数设置为种群规模为100，迭代次数为200，初始交叉概率为0.8，初始变异概率为0.2。

3.2.1 结果分析

运用遗传算法分别对需求确定 (即为3种情景的均值) 考虑班期 (模式A)、需求确定 (即为3种情景的均值) 不考虑班期 (模式B)、需求不确定考虑班期 (模式C)、需求不确定不考虑班期 (模式D) 分别进行路径优化测试。模式A与模式C的运行效果图分别如图7、图8所示。将模式A与模式C的最优运输方案分别代入模式B和模式D，各模式的具体情况如表5所示。

表5 需求确定与需求不确定运输情况一览表Table 5 List of transportation situation under demand determination and demand uncertainty

图7 模式A运行效果图Figure 7 Performance of mode A

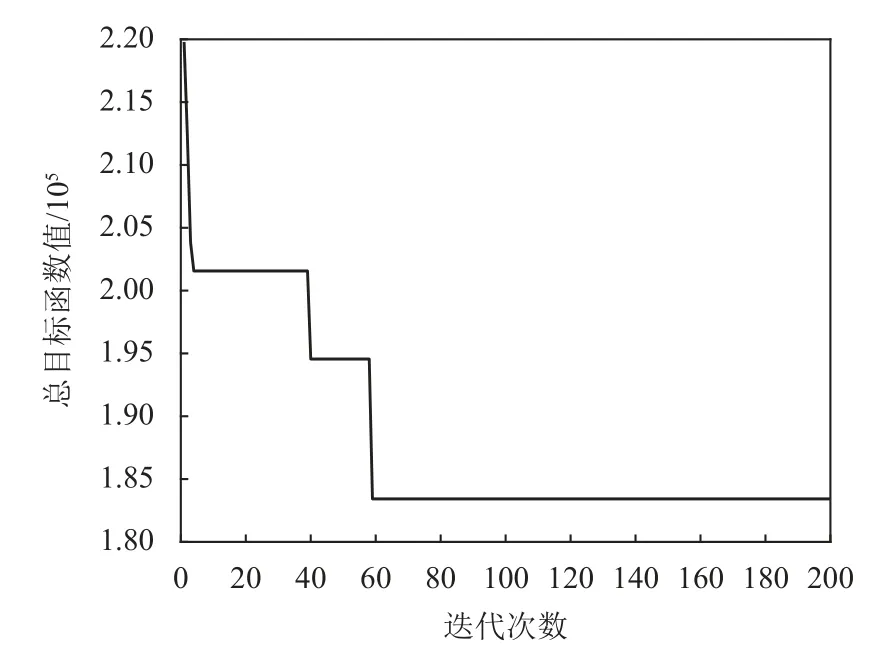
图8 模式C运行效果图Figure 8 Performance of mode C

由图7、图8和表5可知：

1) 模式A的运输路线为“1-2-6-9-13-14”，运输方式为“公-水-水-铁-公”，经济成本为15.40万元，模式C的运输路线为1-4-7-9-11-14，运输方式为公-铁-铁-水-铁，经济成本为18.34万元。对比模式A，模式C的经济成本增加19%，这表明需求不确定会导致经济成本的增加，进而影响运输方案的制定。

2) 相较模式A，模式C的碳排放量降低32%，再结合运输方式的单位碳排量：公路＞水路＞铁路运输，充分说明运用鲁棒优化处理需求不确定问题会对运输全程的碳排放起到遏制作用。

3) 对比模式A与模式B、模式C和模式D的等待时间和等待成本，可知班期存在会产生等待时间，但在收货时间窗约束下，班期对运营时间和经济成本的影响较小。

3.2.2 鲁棒性分析

将模式C的运输方案分别带入低、中、高货运量需求的情景中，得到3种情景下对应的经济成本、碳交易成本和碳排放量，并将其与模式A低、中、高货运量需求最优解的经济成本、碳交易成本和碳排放量进行对比，结果如表6所示。

表6 各情景总成本情况一览表Table 6 List of total costs in each scenario

由表6可知，模式C中对应的低、中、高货运量需求的经济成本均大于模式A中对应情景最优解的经济成本。这证实鲁棒优化在需求波动时，仍能保证运输方案是可行的，它是一种意在保持系统稳定性的求解方式，可使得模型具备鲁棒性及求解结果具备保守性，进而导致经济成本的增加。然而，模式C中对应的低、中、高货运量需求的碳排放量均小于模式A中对应情景最优解的碳排放量，再次验证鲁棒优化在求解此类问题保证了低碳运输。

为更深入研究鲁棒优化在求解路径优化问题的稳定性，对最大遗憾值β进行灵敏度分析，得到其经济成本随最大遗憾值β变化情况如图9所示。

图9 模式C的经济成本随最大遗憾值的变化图Figure 9 The economic cost of mode C as a function of the maximum regret value

由图9可知，经济成本随最大遗憾值的增加而减小，当β∈[0.0,0.3]时，经济成本的降低速度缓慢；当β∈[0.3,0.4]时，经济成本降低速度加快；当β∈[0.4,0.5]时，经济成本基本保持稳定；显然经济成本不一定会随着多式联运系统的鲁棒性增强而显著增大，所以鲁棒性和经济成本之间的关系是值得反复斟酌调控的。因此，企业需要结合自身实际需求来衡量最大遗憾值和经济成本之间的关系，去追求经济成本和系统稳定性之间最佳性价比，进而实现多式联运各参与方的共赢。

基于此，针对组成总经济成本的低、中、高需求情景的成本来深入剖析，得到最大遗憾值对不同情景经济成本的作用效果，如图10所示。

图10 最大遗憾值对各情景经济成本的影响Figure 10 The influence of the maximum regret value on the economic cost of each scenario

由图10可知，当β∈[0.0,0.3]时，低、中、高需求情景下的经济成本的变化幅度较小；当β∈[0.3,0.4]时，低、中需求情景下的经济成本降低，高需求情景下的经济成本增加；当β∈[0.4,0.5]时，低、中、高需求情景下的经济成本基本保持稳定。由此看来，最大遗憾值与经济成本之间是有详细的影响路径，它是通过作用于系统中各需求情景下经济成本的波动水平，从而影响系统的总经济成本。多式联运经营人可以参考自身运营的实际情况去选择适宜的最大遗憾值，使得其在面对波动的需求市场时，仍然可以保持系统的稳定性、实现低碳环保和效益最大化。

4 结论

在碳交易政策下，综合考虑铁、水路班期与收货时间窗，研究需求不确定下多式联运路径优化的问题，建立以经济成本最小为优化目标的需求不确定下多式联运鲁棒优化模型，采用遗传算法进行算例分析。研究结果表明，当需求不确定时，虽会导致经济成本增加，但采用鲁棒优化处理需求波动会有效控制碳排放，使得运输方案选择更侧重于低碳运输；在收货时间窗前提下，班期对经济成本和运营时间的影响甚微；面对动态化的需求市场，多式联运经营人可通过衡量最大遗憾值和经济成本之间的关系，去调配各承运人的运输资源，规划最佳的运输方案，进而达到提升运输效率及实现交通运输的节能减排目的。