Impact of distance between two hubs on the network coherence of tree networks∗

Daquan LI,Weigang SUN,Hongxiang HU

School of Sciences, Hangzhou Dianzi University, Hangzhou 310018, China

Abstract: We study the impact of the distance between two hubs on network coherence defined by Laplacian eigenvalues.Network coherence is a measure of the extent of consensus in a linear system with additive noise.To obtain an exact determination of coherence based on the distance,we choose a family of tree networks with two hubs controlled by two parameters.Using the tree’s regular structure,we obtain analytical expressions of the coherences with regard to network parameters and the network size.We then demonstrate that a shorter distance and a larger difference in the degrees of the two hubs lead to a higher coherence.With the same network size and distance,the best coherence occurs in the tree with the largest difference in the hub’s degrees.Finally,we establish a correlation between network coherence and average path length and find that they behave linearly.

Key words: Consensus;Coherence;Distance;Average path length

1 Introduction

Complex networks are currently attracting an enormous amount of attention in the scientific community and have proved to be a powerful tool for characterizing complex systems (Newman,2003;Gao W et al.,2022a,2022b).Among the network models,deterministic networks (Comellas et al.,2000;Barabási et al.,2001;Comellas and Sampels,2002) are based on recursive techniques and can provide exact results for the studied network metrics,e.g.,degree distribution (Liu et al.,2022),random walks (Gao L et al.,2021;Zaman,2022;Yu XD et al.,2023;Zaman and Ullah,2023),spanning trees (Li et al.,2020;Zaman et al.,2022),and synchronizability (Zhu et al.,2021).In the studies of deterministic network models,fractal networks have been widely studied,such as Apollonian networks (Andrade et al.,2005),Koch networks (Zhang ZZ et al.,2009),Sierpiński networks (Imran et al.,2017),and recursive trees (Peng et al.,2014).

As a typical collective behavior in multi-agent systems,consensus problems have gained increasing interest because of wide applications in diverse fields (Olfati-Saber and Murray,2004;Ren et al.,2007;Yu WW et al.,2010;Lu and Liu,2019;Hu X et al.,2021;Zhang LZ et al.,2022).Consensus describes the process by which groups of agents reach agreement on a common value or state.For example,the directions of a group of unmanned aerial vehicles (Rao and Ghose,2014) are consistent in a formation problem.During the consensus of multi-agent systems,they may be subject to external disturbances (Wang and Liu,2009).In this setting,the agents could not reach consensus.To characterize the system resistance to the disturbances,Patterson and Bamieh (2014) introduced the concept of network coherence.It was proved that coherence is wholly determined by the Laplacian spectrum of the underlying network.Therefore,network coherence allows investigation of the interplay between network structures and the consensus resistance to the noise (Liu et al.,2021).For example,the fractal dimension of Vicsek fractals is related to the scaling of network coherence,but this result does not hold for a family of recursive trees (Sun et al.,2014).

Because the eigenvalues of the Laplacian matrix are often dominated by the network topology (Grone et al.,1990),it is difficult to obtain exact network coherence results quantified by the sum of the reciprocals of all nonzero Laplacian eigenvalues.For some deterministic networks (e.g.,symmetric star topology networks (Gao HP et al.,2022)),great effort has been made to obtain analytical solutions of the network coherence.Hong et al.(2020) studied the relationship between coherence and the number of initial nodes and showed that a smaller number of initial nodes leads to better coherence.Dai et al.(2017) studied the first-order network coherence of weighted Cayley networks by the mean first-passage time and showed that the scalings of coherence regarding the network size obey four types of laws based on the weight factor.Later,Jing et al.(2021) chose a family of ring-trees networks and obtained analytical network coherence solutions using the recursive relations of the Laplacian eigenvalues.Yi et al.(2022) showed that the second-order consensus dynamics with random additive disturbances are related to the concept of biharmonic distance.

It is known that the hub nodes play an important role in dynamic behavior.For example,the hub nodes inhibit the outbreak of epidemics on scale-free networks (Zhang HF et al.,2010).Hu TC et al.(2022) investigated the noise consensus dynamics in a family of tree networks with two hubs and found that a larger difference in the degrees of the hub nodes leads to better coherence.In addition,Chen et al.(2023) showed that the network with one hub displays better leader-follower coherence than networks with two hubs.To our knowledge,few results involve the impact of the distance between two hubs on the studied coherence.Inspired by the above discussions,we choose a family of tree networks with two hubs as our model and investigate the impact of distance on coherence.The aim of the present work is to obtain exact solutions of the coherence regarding the distance and to further study the relationship between coherence and average path length in an analytical form.

2 Preliminaries

2.1 Network models

To study the effect of the distance between two hubs on coherence,we introduce a parameterdmeasuring the distance between two hubs.The asymmetry of the trees is changed by the hub’s degrees.In the following,we propose a family of tree networks with two hubs where the distance between the two hubs remains unchanged by adjusting the degrees of the two hubs.The detailed operation of this tree network model is summarized in Fig.1.

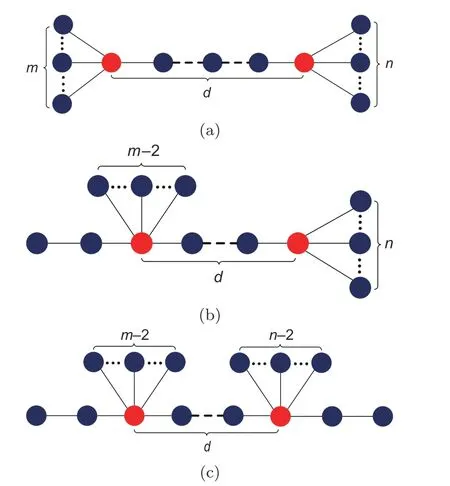
Fig.1 A family of tree networks with the same distance d between two hubs: (a) T1;(b) T2;(c) T3.The parameters m and n control the tree’s asymmetry,and the network size is N=m+n+d+1

2.2 Network coherence

Patterson and Bamieh (2014) proposed the concept of network coherence,which characterizes the extent of consensus resistance to external noise.The governing equation of a consensus system with additive noise is given by

wherex(t)=(x1(t),x2(t),...,xN(t))Tis the system’s state,Nis a positive integer denoting the network size,andL=(Lij)N×Nis the Laplacian matrix where the elements are defined as follows:off-diagonal elementsLij= -1 if nodeiis adjacent to nodejand 0 otherwise,and the diagonal elementsLiiare the nodes’degrees.η(t) is a zero-mean,unitvariance white noise process.

When there is no noise in system (1),the system will asymptotically converge to consensus.Conversely,system (1) does not reach consensus due to the existence of noise terms.To measure the extent of consensus around the average of current node states,Patterson and Bamieh (2014) introduced the concept of network coherence,which is defined by the mean steady-state variance of the deviation from the average of all node states,that is,

It has been shown that the coherenceHis completely determined by the Laplacian eigenvalues (Xiao et al.,2007;Bamieh et al.,2012),i.e.,

whereλi(i=1,2,...,N) are the Laplacian eigenvalues,and 0=λ1<λ2≤λ3≤...≤λN.

Lemma 1Letp(x)=αnxn+...+α1x+α0be a real polynomial of degreen ≥2 withα0/=0.We have

whereρk(k=1,2,...,n) are the roots ofp(x)(Karayannakis and Aivalis,2018).

3 Exact calculations of network coherence

In this section,we present a method for obtaining the analytical expressions of network coherence defined in Eq.(2) of treesT1,T2,andT3in Fig.1.Hi(i=1,2,3) represents the coherence of treeTi.According to the structure ofT1,its Laplacian matrixL1reads as

whereIis an identity matrix of orderm+nand

To obtain the solution to Eq.(2),we need to calculate the characteristic polynomialP1(λ) forL1.Using the elementary row operations on this determinant,we transformP1(λ) into a tridiagonal determinant and further expandP1(λ) by row expansion of this determinant.The detailed operations are as follows:

The tridiagonal determinantUk(λ) of orderkreads as

According to Eq.(3),we obtain a recursive relation in the form below:

whereUk(0),Uk(1),andUk(2) are the coefficients of the constant,first-order,and second-order terms ofλ,respectively.

Because there is a zero eigenvalue of the Laplacian matrixL1,we need to introduce a new polynomialto obtain all the nonzero eigenvalues.Based on Lemma 1,we determine the coefficients to obtain an exact solution of network coherence.The coefficients are

For treeT2,we reduce the degree of the leftmost hub to prevent the distance from changing.In the same way,we obtain coherenceH2in the following form:

Further,we reduce the degrees of both hubs to form treeT3.Its Laplacian matrix is

The corresponding characteristic polynomialP3(λ) for matrixL3becomes

Finally,we obtain a solution of coherenceH3as follows:

4 Robustness of network coherence

This section presents our study of the robustness of coherencesH1,H2,andH3regarding distancedand network parametersmandn.First,we plot the distributions of coherencesH1,H2,andH3against distancedbetween two hubs in Fig.2,which shows that the network coherence is better with a smaller distance.According to Eqs.(5)-(7),we further obtain

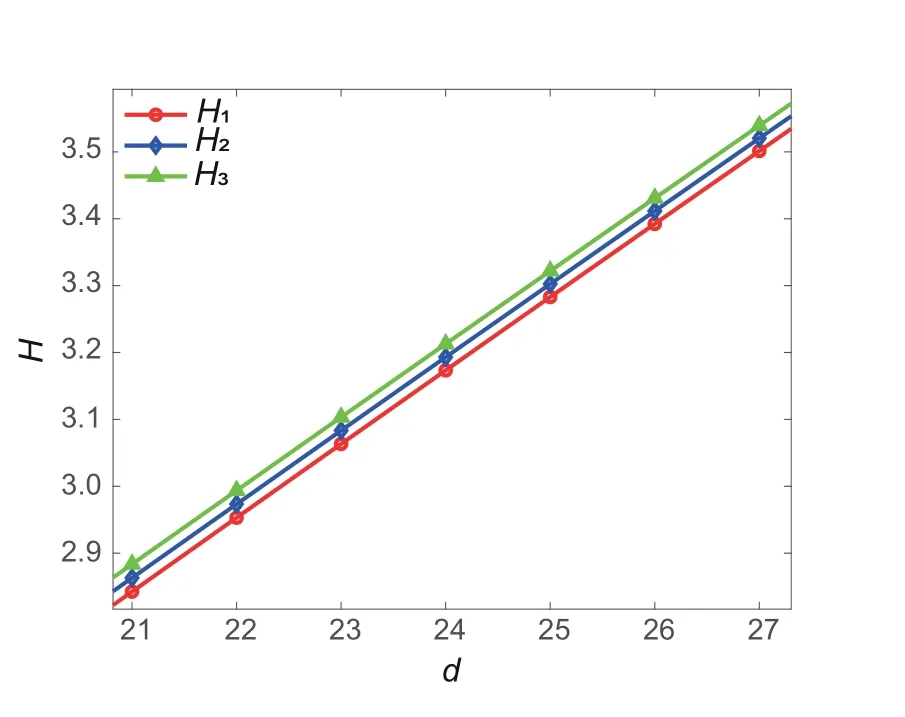
Fig.2 Distributions of coherences H1,H2,and H3 against distance d with m=30 and n=20

It then follows thatH3>H2>H1,becacuseN=m+n+d+1>3,meaning that the coherence of treeT1is the best.

Second,we investigate the effect of parametersmandnon the coherence with a fixed network sizeNand distanced.Expression (5) gives

Becauseφ1>0,coherenceH1achieves the maximum valuewhenm=n.On the other hand,H1reaches the minimum when |m-n|is the maximum.It then shows that the larger the difference between the degrees of the two hubs,the higher the coherence.In Fig.3,we plot the coherence change regarding parameterm,verifying the effectiveness of the above analysis.

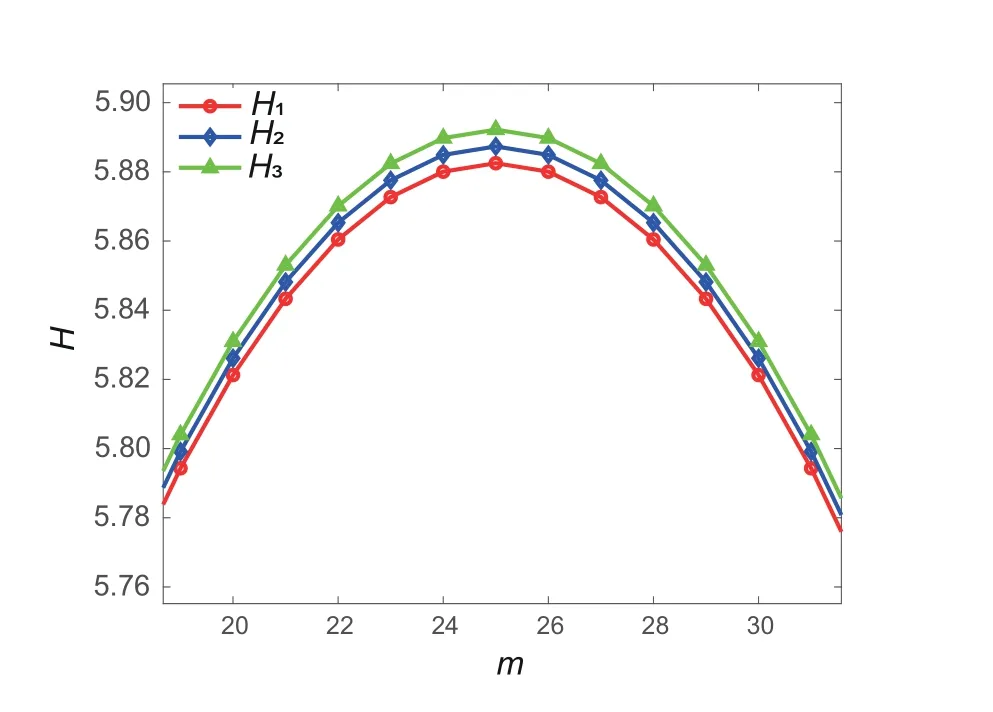
Fig.3 Distributions of coherences H1,H2,and H3 against parameter m with N=100, d=49,and n=50-m

Finally,we show the phase diagrams of coherencesH1,H2,andH3in a two-dimensional space (m,n) in Fig.4.In summary,a larger difference of parametersmandnleads to a better coherence.

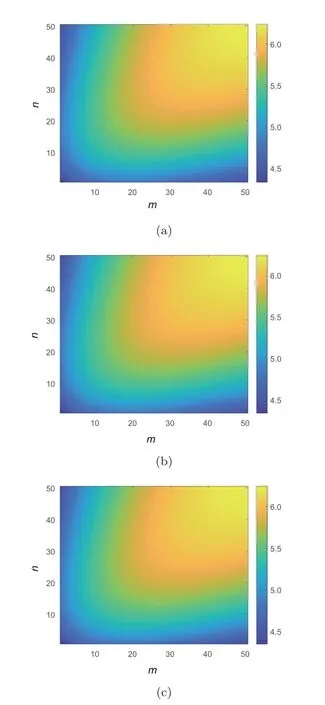
Fig.4 Phase diagrams for coherences H1 (a), H2 (b),and H3 (c) in a two-dimensional space (m, n) with d=49

5 Relationship between coherence and average path length

We identify a relationship between the coherence and average path length.In network science,the average path length (APL) is defined as the average distance between any two nodes,which is a measure of the efficiency of information transfer on a network.It is defined as

wheredijis the shortest distance between two nodes.Using the tree’s regular structure,the exact expressions of APL are given by

From the expressions of the coherences (Eqs.(5)-(7)) and the average path lengths (Eqs.(8)-(10)),we find that the coherence value increases with the increase of the average path length at a linear rate.When the parameters are the same (m=n),the average path length is the largest,which means that the coherence is the worst.Conversely,when there is a larger difference in the hub’s degrees (i.e.,|m-n|),the average path lengths become smaller,showing that the trees display better coherence.In Fig.5,we plot the linear relationship between coherenceH1and average path length APL1.Similar results hold for treesT2andT3.

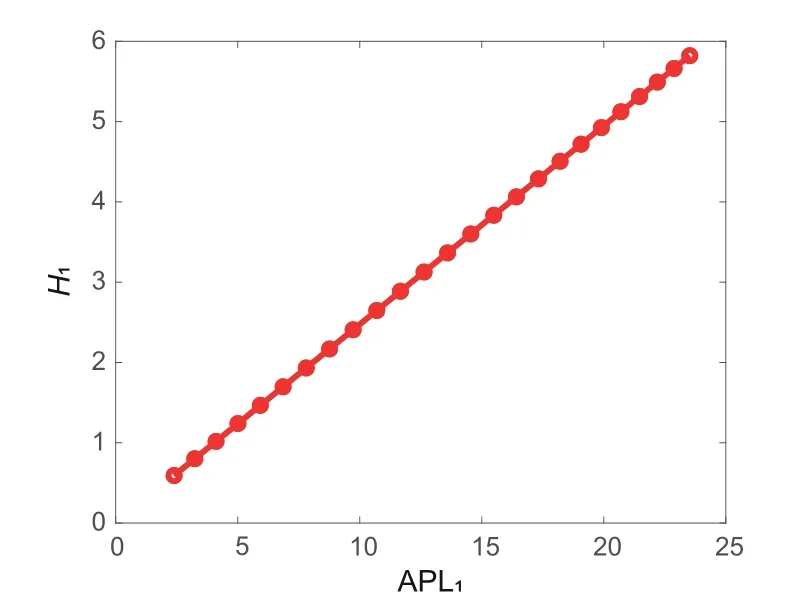
Fig.5 Relationship between coherence H1 and average path length APL1 with N=100,m=30,and n=69-d

6 Conclusions

In this study,we investigated the impact of the distance between two hubs on network coherence and chose a family of tree networks as an example.The main feature of this kind of tree is that the degrees of two hubs are adjusted using two parameters to maintain the same distance between the hubs.We then obtained the analytical solutions of the coherence based on the tree’s structure and found that the coherence robustness is significantly affected by the distance and the degrees of the hubs.A smaller distance between two hubs and a larger difference between the degrees will result in a higher coherence.We also studied the relationship between the coherence and average path length and showed that the tree displays higher coherence when the average distance is smaller.Because the Laplacian eigenvalues are related to the network topology,how to obtain generalization results for real-world networks is an interesting problem with technical challenges,leaving some related work to be carried out in the future.

Contributors

Weigang SUN guided the research.Daquan LI,Weigang SUN,and Hongxiang HU contributed to the conceptualization and methodology of the study.Daquan LI and Weigang SUN performed the formal analysis and drafted the paper.Weigang SUN and Hongxiang HU revised and finalized the paper.

Compliance with ethics guidelines

Daquan LI,Weigang SUN,and Hongxiang HU declare that they have no conflict of interest.

Data availability

The data that support the findings of this study are available from the corresponding author upon reasonable request.