A home energy management approach using decoupling value and policy in reinforcement learning∗

Luolin XIONG ,Yang TANG ,Chensheng LIU ,Shuai MAO ,Ke MENG ,Zhaoyang DONG,Feng QIAN

1Key Laboratory of Smart Manufacturing in Energy Chemical Process, Ministry of Education,East China University of Science and Technology, Shanghai 200237, China

2Department of Electrical Engineering, Nantong University, Nantong 226019, China

3School of Electrical Engineering and Telecommunications,University of New South Wales, Sydney NSW 2052, Australia

4School of Electrical and Electronics Engineering, Nanyang Technological University, Singapore 639798, Singapore

Abstract: Considering the popularity of electric vehicles and the flexibility of household appliances,it is feasible to dispatch energy in home energy systems under dynamic electricity prices to optimize electricity cost and comfort residents.In this paper,a novel home energy management (HEM) approach is proposed based on a data-driven deep reinforcement learning method.First,to reveal the multiple uncertain factors affecting the charging behavior of electric vehicles (EVs),an improved mathematical model integrating driver’s experience,unexpected events,and traffic conditions is introduced to describe the dynamic energy demand of EVs in home energy systems.Second,a decoupled advantage actor-critic (DA2C) algorithm is presented to enhance the energy optimization performance by alleviating the overfitting problem caused by the shared policy and value networks.Furthermore,separate networks for the policy and value functions ensure the generalization of the proposed method in unseen scenarios.Finally,comprehensive experiments are carried out to compare the proposed approach with existing methods,and the results show that the proposed method can optimize electricity cost and consider the residential comfort level in different scenarios.

Key words: Home energy system;Electric vehicle;Reinforcement learning;Generalization

1 Introduction

With recent advances in the field of electric vehicles (EVs) and intelligent household appliances,flexibility on the demand side is increasing (Parag and Sovacool,2016;Wen et al.,2021).Meanwhile,fluctuating renewable energy resources bring uncertainties to the energy-supply side (Agnew and Dargusch,2015;Luo et al.,2020),which have greatly driven the rapid growth of home energy management (HEM) techniques to adjust energy consumption according to real-time electricity prices and flexible renewable energy generation.Efficient HEM techniques are promising in optimizing electricity cost,comforting residents,and reducing carbon emissions,which are achieved by intelligently scheduling and controlling EVs and household appliances (Liu YB et al.,2016;Xia et al.,2016;Hu et al.,2018;Mao et al.,2019).

Numerous investigations have been carried out into feasible strategies of HEM from the demandside perspective (Li HP et al.,2020b;Luo et al.,2020;Kong et al.,2021).In the literature,HEM approaches are divided mainly into two categories: model-driven approaches and data-driven approaches (Xu et al.,2020;Xiong et al.,2022).Modeldriven methods are superior in terms of reducing the computational burden and alleviating data dependence.For instance,a multi-objective mixed-integer nonlinear programming model has been developed to optimize energy use in a smart home (Anvari-Moghaddam et al.,2015).In this work,a tradeoffbetween energy saving and a high comfort level was considered,and the running of the proposed model-driven algorithms can be finished within several seconds.A probabilistic optimization problem has been designed for HEM in a renewable-energybased residential energy hub,where the two-point estimation method has been developed to model the uncertainty in the output power of solar panels,and less than 1 min was required for running the proposed HEM program (Rastegar et al.,2017).A new framework has been proposed with related analysis models to determine optimal demand response strategies,where resident occupancy behavior and forecasted renewable energy generation have been estimated (Baek et al.,2021).However,the scalability of these model-driven approaches in different scenarios is poor,and re-established models are a prerequisite for excellent performance in new scenarios.Moreover,the performance of these modeldriven methods is dependent heavily on complex system models,the accuracy of which is hard to be guaranteed with multiple uncertainties (Shi et al.,2023).

To tackle these challenges encountered by model-driven approaches,data-driven approaches have gained particular research attention in HEM (Shirsat and Tang,2021;Huang et al.,2022;Liu SG et al.,2022).A data-driven distributional optimization method has been proposed to guarantee robustness against the worst probability distribution of multiple uncertainties (Saberi et al.,2021).In this study,the authors have pointed out that probability distributions always have errors,even under the assumption that the accurate probability distributions of uncertainties are known.Furthermore,with the rapid development of artificial intelligence technology,the optimization problems of complex largescale energy systems have been solved by intelligent dynamics optimization methods (Qian,2019,2021;Gao et al.,2022).As an emerging phenomenon of artificial intelligence techniques,reinforcement learning (RL) has attracted considerable attention due to its data-driven outstanding decision-making capability and superhuman performance in a number of challenging tasks (Wang HN et al.,2020;Wang YP et al.,2021;Tang et al.,2022;Wang JR et al.,2022).RL techniques are typically used in HEM,and there exist two kinds of approaches: value-based RL and policy-based RL (Xiong et al.,2021).Valuebased RL algorithms estimate an action-value table or function and choose the action with the maximum value according to the table or function.Therefore,value-based algorithms can be used only for tasks with discrete actions.For example,to propose a secure demand response management scheme for HEM,Q-learning has been adopted to make optimal price decisions using Markov decision process (MDP) with the objective of reducing energy consumption,which has benefited both consumers and utility providers (Kumari and Tanwar,2022).

For tasks with high-dimensional action space (such as control of mass appliances) or continuous action space (such as charging control of EVs),it is challenging for value-based algorithms to achieve excellent performance (Qin et al.,2021).Consequently,methods combining value-and policy-based algorithms,such as deep deterministic policy gradient (DDPG) (Zenginis et al.,2022) and advantage actor-critic (A2C) (Shuvo and Yilmaz,2022),have been used more extensively in HEM.For instance,a novel privacy-preserving load control scheme based on the vectorized A2C algorithm has been developed to tackle high-dimensional action space and the partial observability of state for the residential microgrid,in which the microgrid operator manages a multitude of home appliances,including EVs and air conditioners (Qin et al.,2021).Due to the random nature of electricity prices,appliance demand,and user behavior,a novel reward shaping based actorcritic deep RL (DRL) algorithm has been presented to manage the residential energy consumption profile with limited information about the uncertain factors (Lu et al.,2023).In these methods,accurate estimation of the value function can instruct the HEM agent to learn the most valuable policies and contribute to remarkable performance.

However,these standard DRL algorithms usually use shared networks for the policy and value functions,which therefore limits the estimation accuracy of the value function (Raileanu and Fergus,2021).Since the value function estimation requires more information than the policy function estimation,shared networks for the policy and value functions can easily lead to overfitting.

Motivated by the aforementioned phenomenon,in this work,we introduce a decoupled A2C (DA2C) algorithm with separate networks for the policy and value functions to mitigate the overfitting problem in HEM.Different from existing RL algorithms with shared networks for the value and policy functions,which suffer from poor generalization (Li HP et al.,2020a),the DA2C algorithm proposed in Raileanu and Fergus (2021) can not only achieve outstanding performance in reducing the electricity cost and comforting the residents but also show good generalization to new scenarios with different residents and different seasons.The main contributions of this paper are summarized as follows:

1.Multiple uncertainties affecting the dynamic charging behavior of individual EVs,such as driver’s experience,unexpected events,and traffic conditions,are integrated into an improved mathematical model.Compared with the model proposed in Yan et al.(2021),the improved EV-charging model describes the energy demand of EVs more exactly.

2.The DA2C approach with separate networks for the policy and value functions is developed to schedule the charging operation of EVs and the energy consumption of household appliances in smart homes.Compared with existing RL algorithms used in HEM (Li HP et al.,2020a),the DA2C algorithm enhances the generalization by decoupling value and policy to alleviate the overfitting problem.

3.A set of experiments are conducted to verify the performance of the proposed data-driven intelligent optimization method.Compared with existing methods,our proposed method shows competitive performance in optimizing electricity cost and comforting the residents even in different scenarios.

2 Problem formulation

As shown in Fig.1,this work aims at developing a data-driven intelligent optimization method based on RL to achieve optimal energy management of smart home systems,by appropriately scheduling the charging operation of EVs and the energy consumption of household appliances on the demand side.In this section,an improved mathematical model describing the dynamic energy demand of individual EVs,which integrates various uncertain factors,is proposed first.Furthermore,we formulate the HEM problem as an MDP,in which the charging operation of private EVs and the energy consumption of household appliances are regarded as the actions to be optimized.

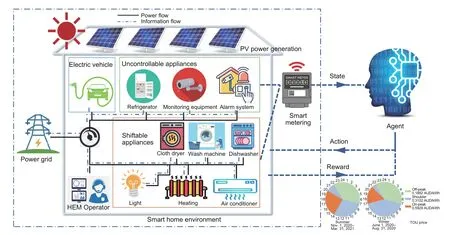
Fig.1 Reinforcement learning based home energy management system (PV: photovoltaic)

2.1 Improved EV-charging model

In the HEM problem,the charging operation of private EVs is worthy of in-depth consideration owing to its complex characteristics compared with other household appliances (Zhang YA et al.,2022;Zhang YI et al.,2022).The charging operation depends directly on the energy demand of EVs’ batteries.Consequently,we present an improved EVcharging model to describe the energy demand of EVs,which is comprehensively affected by a wide variety of uncertain factors,such as driver’s experience,unexpected events,and traffic conditions.

Remark 1Specifically,experienced drivers may not charge frequently,compared to novices,to make sure that the state of charge (SoC) always remains at a high level,and they are more tolerant to the anxiety of power depletion.Unexpected events may prompt the EV to leave before the preset departure time,and sudden termination of charging will lead to a lack of energy for the subsequent trip.Besides,traffic conditions have a significant impact on the charging behavior,even if the drivers are experienced.When encountering congestion,accidents,extreme weather,special events,and other costly delays,driver’s experience often fails,leading to increased anxiety.Consequently,an improved EVcharging model is presented with the aforementioned uncertain factors integrated.

First,as shown in Eq.(1),the dynamics of the EV batteries are modeled with two modes: charging and discharging:

Next,the charging operation of individual EVs is determined by driver’s anxiety about the SoC,which is further affected by multiple uncertainties including driver’s experience,unexpected events,and traffic conditions.It is obvious that conservative drivers with less experience need to ensure a higher SoC level for departure.As the experience increases,drivers can estimate the energy required for the journey more accurately,and the anxiety level will decrease.In addition,it is worth noting that the traffic conditions may affect drivers’ judgment of the energy demand for the journey,even for experienced drivers.For example,when traffic jams occur due to extreme weather or traffic accidents,more energy is needed for the same journey.Similarly,when the temperature is high (in summer) or while encountering cold weather conditions (in winter),the use of air conditioning in the EV will lead to more energy consumption.All of the above may cause inaccurate estimation of energy required,which in turn incurs an escalation of anxiety.Here,we describe driver’s anxiety with the expected SoCZSoC(t) in Eq.(5),which integrates the aforementioned uncertainties comprehensively (Yan et al.,2021):

wheretaandtdrepresent the arrival time and the departure time respectively,andt ∈(ta,td].k1∈[0,1],k2∈(-∞,0)∪(0,+∞),andk3∈[0,1]are the shape parameters changing with driver’s experience,unexpected events,and traffic conditions,respectively.

Whent=td,ZSoC(t)=k1k3shows that the expected SoC is determined by parametersk1andk3.In other words,the value ofk1k3reflects the anxiety level of the driver at departure timetd,which is related to driver’s experience and traffic conditions.Hence,driver’s experience and traffic conditions can be characterized by parametersk1andk3,respectively.Whenk1k3=1,the expected SoCZSoC(t) is determined byk2,and these three kinds of uncertainties can be described by the combination ofk1,k2,andk3.A higher SoC during the charging duration corresponds to largerk1,k2,andk3values.Hence,drivers can set the values ofk1,k2,andk3according to their actual situation.

2.2 MDP formulation

With the improved EV-charging model,the scheduling problem of home energy is then formulated as an MDP containing four elements,whereS,A,R,andPrepresent the state set,action set,reward function,and state transition probability,respectively.Detailed definitions for these four elements in HEM are presented as follows:

1.State: The statestcontains the energy consumption information of the smart home at time slott:

whereλtis the time-of-use electricity price,andrepresents solar photovoltaic (PV) power generation.Moreover,are the energy consumptions of uncontrollable appliances and shiftable appliances,respectively,at time slott.

2.Action: The actions are defined as follows:

3.Reward: To achieve the objectives of minimizing the electricity cost and comforting the residents,the reward function integrates the electricity cost and the residential discomfort through weighted coefficientsβ1,β2,andβ3.Residents’discomfort is quantified by the dispatching energy consumption of shiftable appliances and the anxiety about the EV’s SoC level.

whereγ ∈[0,1] is the discount factor for future decisions.

4.Transition: The system state transition reveals the change of system statestaccording to actionat.The transition ofcan be depicted by the dynamics of EV batteries shown in Eq.(1).Besides,electricity prices,PV power generation,and power consumption of uncontrolled appliances fluctuate stochastically,which also constitute the transition of the system states.

Remark 2Note that time slottrepresents an interval of half an hour.Within half an hour,the prices,PV power generation,and energy consumption in statestare assumed to be constant.The actions also remain constant in half an hour.

3 Proposed approach

In this section,the detailed DA2C algorithm is presented,in which the value network and the policy network are decoupled to meet differentiated information demand for value function estimation and policy function estimation.

It has been already proved that the accurate estimation of the value function requires more information than learning of the optimal policy (Raileanu and Fergus,2021).The widely used shared networks for the policy and value functions can cause overfitting,which also results in poor generalization performance of RL.However,in the HEM problem,the RL agent encounters various scenarios due to the change in power consumption habits caused by different residents and the change in PV power generation caused by seasonal switching.The generalization performance is critical for the scheduling schemes.An intuitive approach is to provide two completely independent networks,representing the value network and the policy network,as shown in Fig.2.

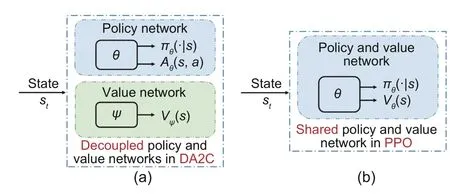
Fig.2 Comparison of decoupled architecture in DA2C (a) and shared architecture in PPO (b) (DA2C: decoupled advantage actor-critic;PPO: proximal policy optimization)

Nevertheless,due to the inaccessibility of the policy network to the gradients from the value function,the agent struggles to learn the optimal policy effectively and suffers from worse training performance compared with approaches using shared network (Cobbe et al.,2021).In fact,the learning process of the policy network rests largely on gradients from the value function for the reason that gradients from the policy function are drastically sparse and show high variance (Raileanu and Fergus,2021).On the contrary,gradients from the value function are denser and less noisy.Accordingly,an auxiliary loss consisting of the advantage is introduced to guide the training of the policy network,which is a relative measure of the action value.Moreover,it is worth emphasizing that networks of the RL agent should be relatively shallow to ensure fast fitting in the HEM problem compared with deeper networks in the field of image processing.Besides,larger networks are not accepted because excessive redundant parameters may aggravate overfitting (Ota et al.,2020).

In detail,we use two separate networks to represent the policy function and the value function,as depicted in Fig.3.The policy network is parameterized withθ,which is trained to learn the optimal scheduling policyπθ(st) and the advantage functionAθ(st,at).The value network is parameterized withψand is adopted to predict the value functionVψ(st).Then,the objective of the policy network and the loss of the value network are depicted as follows:

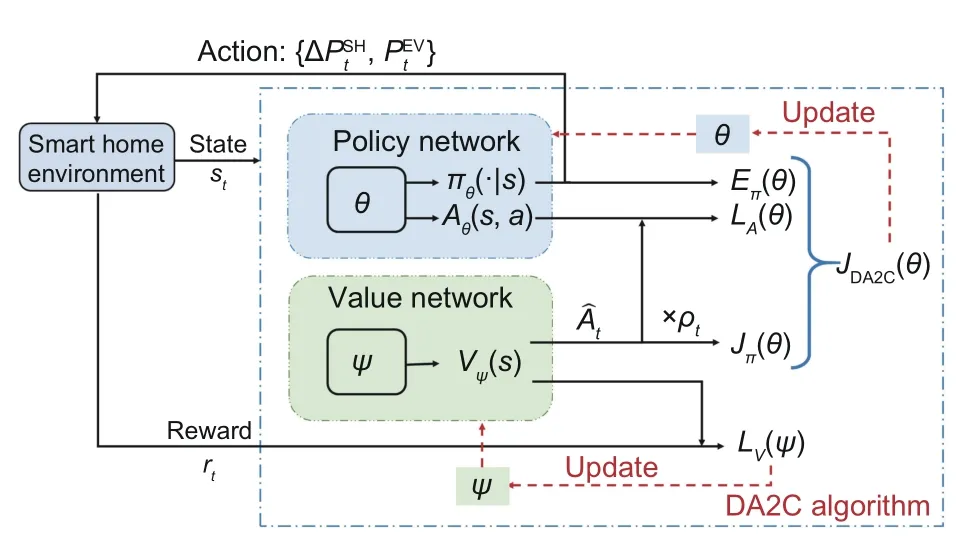
Fig.3 Decoupled advantage actor-critic (DA2C) algorithm

The objective of the policy network is represented by the following expression:

whereJπ(θ) is the policy gradient objective,as shown in Eq.(11).It is the same as the objective in the classic proximal policy optimization (PPO) algorithm (Schulman et al.,2017).Eπ(θ) is the entropy used to encourage exploration,LA(θ) is the auxiliary advantage loss,providing a useful gradient for training the policy network,andρeandρarepresent the weights corresponding to the importance of the entropyEπ(θ) and the lossLA(θ),respectively.

Specifically,the policy gradient objective is defined as follows:

The auxiliary advantage loss is presented as

whereAθ(st,at) is one of the policy network’s outputs.

The loss of the value network is represented by the following expression:

Since two separate networks are used to learn the policy and value functions,the learning process of each network can be decoupled and different updating frequencies are allowed.It has been found that the value network allows for larger amounts of sample reuse than the policy network (Cobbe et al.,2021).Hence,it is worth exploring whether updating the value network for everynupdates of the policy network contributes to better performance and training stability.The pseudo-code of the proposed DA2C is displayed in Algorithm 1.

4 Experiments and results

The effectiveness of the proposed DA2C approach in HEM is verified in scheduling tasks of various residents with different electricity preferences.Moreover,the generalization to unseen scenarios of the learning algorithm is confirmed.In this section,the experimental setup is described first.Then,the optimization results and generalization performance compared with other approaches are verified,and the corresponding discussion is provided.Finally,the analysis of the hyperparameters is shown,including the value ofnand the trade-offbetween electricity cost and residential comfort level.

4.1 Experimental setup

For the evaluation of the proposed HEM scheme,the dataset and the hyperparameters are first presented in this part.We consider the energy scheduling of intelligent appliances and EVs during one day,with 30 min as one time slot,such that the time horizonTis 48.The dataset consists of four randomly selected residents in the Australian grid,who are billed on a domestic tariffand have a gross metered solar system installed from July 1,2010,to June 30,2013(Ausgrid,2014).The real-world power consumption data of household appliances and PV power generation data are also obtained from the above dataset.The time-of-use electricity prices have been obtained from Zhou (2020),which are different in the off-peak,shoulder,and on-peak periods,and the division of time periods is different in summer and winter.Other parameters concerning the RL algorithm are reported in Table 1.Both the policy network and the value network consist of three fully connected layers,each with 100 neurons.It is worth noting that 10 trials are implemented for each of the experiments,and the experiments are implemented on Python 3.6.13 with the machine learning package PyTorch 1.8.1.

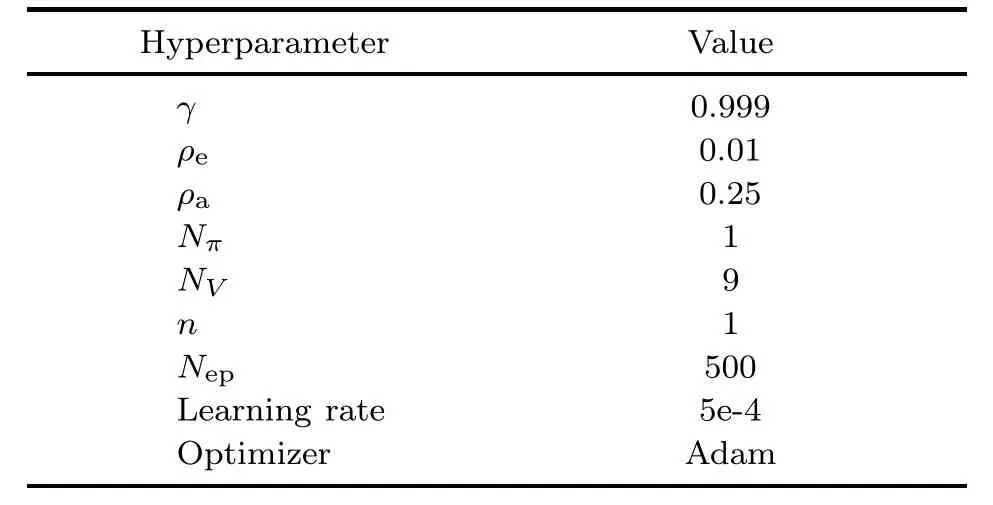
Table 1 List of hyperparameters used in the proposed DA2C approach

4.2 Performance comparison

In this case,an HEM scheme for different residents with different electricity preferences is designed to verify the generalization performance of the proposed approach under dynamic electricity prices in different seasons.We first divide the scheduling tasks of different residents into the training and test tasks.Specifically,the data from residents 1-3 are used for training,while the data from resident 4 are used for test.Besides,the generalization performance is verified with cross-seasonal tasks.The scheduling tasks during spring,summer,and autumn are viewed as training tasks,and scheduling in winter is the test task.The proposed approach is compared with several benchmarks,such as PPO (Li HP et al.,2020a),invariant decoupled advantage actor-critic (IDAAC) (Raileanu and Fergus,2021),and attention-based partially decoupled actor-critic (APDAC) (Nafi et al.,2022).Besides,to verify the efficacy of the state and reward definitions in the proposed MDP,we compare the proposed MDP with different MDP formulations (Xu et al.,2020).

The method is first tested over resident 4 when the agent is trained over residents 1-3.The generalization performance can be verified due to the differences in power consumption mode and time among different residents.Table 2 shows the training and test performances of different approaches.DA2C outperforms all the methods on both training and test tasks.Fig.4 illustrates the training and test performances on tasks from different residents,where the average (dark line) and the standard deviation (shaded area) are shown.We show comparisons between the RL algorithms: PPO,IDAAC,and APDAC.Our approach,namely DA2C,shows superior results on the training level,relative to the other three methods.In addition,DA2C achieves comparable performance on the test level for the scheduling tasks of resident 4,which further illustrates the superiority of the decoupled policy and value networks in enhancing optimization and generalization performances.

Table 2 Comparison of different methods and different Markov decision processes (MDPs) in terms of training and test performances on tasks from different residents

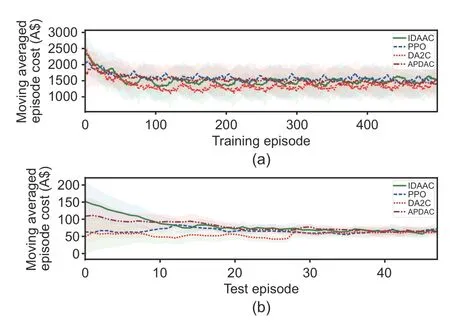
Fig.4 Comparison of different methods in terms of training (a) and test (b) performances on tasks from different residents

Moreover,we define the MDP formulation in Xu et al.(2020) as MDP_1,whose system states,actions,and reward functions are different from those of ours.Obviously,the averaged cost we compared is directly related to the reward function,so we define MDP_2 with the same reward function as our MDP,the same system states and actions as those in Xu et al.(2020).Table 2 demonstrates the efficacy of our MDP.Comparing the results of MDP and MDP_2,it can be found that the system state and action definitions are reasonable and effective since lower cost is achieved with the same algorithm.Results of MDP_1 are better than those of MDP,because the dissatisfaction cost in MDP_1 is related only to the upper bound of energy consumption.In our MDP,the dissatisfaction cost is more comprehensive,integrating uncertainties such as driver’s experience,unexpected events,and traffic conditions,which also leads to higher costs.As shown in Fig.5,our proposed method achieves the best performance in most problems,except for the training process of MDP_1,which also verifies the effectiveness of our method in dealing with generalizable HEM problems.

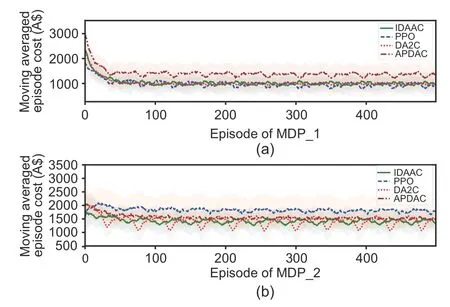
Fig.5 Comparison of different methods with different MDPs in terms of different residents: (a) MDP_1;(b) MDP_2

Besides,we compare the total cost during different seasons,and the agent is tested over winter while being trained over spring,summer,and autumn.The appliances in home energy systems are operated differently in different seasons,such as the heating,ventilation,and air conditioning (HVAC) systems operating in the cooling mode in summer and the heating mode in winter.Table 3 shows the training and test performances of different approaches and reveals that DA2C outperforms the other methods on both training and test tasks.The average (dark line) and standard deviation (shaded area) are depicted in Fig.6 to illustrate the outstanding performance on tasks from different seasons.

Table 3 Comparison of different methods in terms of different seasons

Fig.6 Comparison of different methods in terms of different seasons: (a) training;(b) test

4.3 Analysis of hyperparameters

In this part,we first search for a hyperparameter of the number of value updates,after which we perform a policy updaten ∈{1,8,32}.The results are presented in Fig.7,andn=1 is found to be the best hyperparameter.Therefore,we use this value to obtain the results reported in the paper.

Fig.7 Hyperparameter search n∈{1,8,32}

To further demonstrate the trade-offbetween electricity cost and residential comfort,we change the values ofβ1,β2,andβ3to show the preference of reducing electricity cost and comforting residents.Higherβ2andβ3means that the residents prefer comforting themselves.In contrast,higherβ1reveals higher cost sensitivity and higher tolerance for discomfort.The numerical results obtained from residents with different preferences are shown in Table 4.It is intuitive that residents with higher cost sensitivity have lower total cost and those with higher comfort requirements need to pay more fees.Fig.8 reflects the fact that the cost reduces along with the increase ofβ1.Besides,when the residents prefer comforting themselves,as shown by the blue and red dotted lines in Fig.8,the total cost even increases with the increase of the episodes,which is the cost that must be paid to improve the comfort level.

Table 4 Trade-offbetween electricity cost and residential comfort level

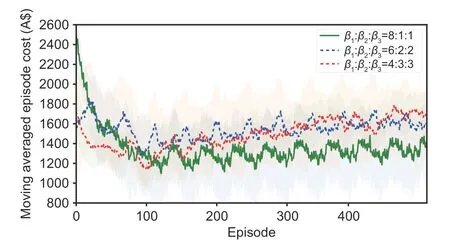
Fig.8 Trade-offbetween electricity cost and residential comfort level (References to color refer to the online version of this figure)

5 Conclusions

In this paper,a data-driven intelligent optimization approach is proposed to achieve optimal energy management of smart home systems,by appropriately scheduling the charging operation of EVs and the energy consumption of household appliances.First,an improved mathematical model is designed to quantify EVs’ energy demand more practically and completely,where driver’s experience,unexpected events,and traffic conditions are integrated.Second,a novel RL-based DA2C approach is developed to alleviate the overfitting problem and enhance generalization performance by decoupling the policy and value networks.Moreover,a set of experiments carried out on practical data from the Australian grid verify the performance and generalization ability of the proposed approach for the HEM problem.In our future work,we plan to extend the approach to more complex large-scale energy systems with multiple uncertainties (Liu ZT et al.,2022,2023;Zhang HF et al.,2022),such as smart home systems with HVAC and combined cooling heating and power systems.Moreover,privacy preservation is an interesting topic in energy systems,which not only guarantees the privacy of residential information but also contributes to cyber-physical security (Li JH,2018;Mao et al.,2021;Wang AJ et al.,2022).

Contributors

Luolin XIONG designed the research.Luolin XIONG,Yang TANG,and Chensheng LIU proposed the methods.Luolin XIONG conducted the experiments.Ke MENG and Zhaoyang DONG processed the data.Luolin XIONG and Yang TANG participated in the visualization.Luolin XIONG drafted the paper.Yang TANG and Shuai MAO helped organize the paper.Yang TANG,Chensheng LIU,Shuai MAO,and Feng QIAN revised and finalized the paper.

Compliance with ethics guidelines

Yang TANG is a guest editor of this special feature,and he was not involved with the peer review process of this manuscript.Luolin XIONG,Yang TANG,Chensheng LIU,Shuai MAO,Ke MENG,Zhaoyang DONG,and Feng QIAN declare that they have no conflict of interest.

Data availability

The authors confirm that the data supporting the findings of this study are available within the article.