Matrix-valued distributed stochastic optimization with constraints∗

Zicong XIA ,Yang LIU ,Wenlian LU ,Weihua GUI

1Key Laboratory of Intelligent Education Technology and Application of Zhejiang Province,Zhejiang Normal University, Jinhua 321004, China

2School of Mathematical Sciences, Zhejiang Normal University, Jinhua 321004, China

3School of Mathematical Sciences, Fudan University, Shanghai 200433, China

4School of Automation, Central South University, Changsha 410083, China

Abstract: In this paper,we address matrix-valued distributed stochastic optimization with inequality and equality constraints,where the objective function is a sum of multiple matrix-valued functions with stochastic variables and the considered problems are solved in a distributed manner.A penalty method is derived to deal with the constraints,and a selection principle is proposed for choosing feasible penalty functions and penalty gains.A distributed optimization algorithm based on the gossip model is developed for solving the stochastic optimization problem,and its convergence to the optimal solution is analyzed rigorously.Two numerical examples are given to demonstrate the viability of the main results.

Key words: Distributed optimization;Matrix-valued optimization;Stochastic optimization;Penalty method;Gossip model

1 Introduction

1.1 Distributed optimization

In recent years,distributed optimization has received great attention thanks to its important role in describing a number of collective assignments.As an effective parallel computing method,distributed optimization can tackle large-scale optimization problems which can be decomposed into several subproblems that can be solved in parallel.Its applications and theoretical significance relate to various fields,including sensor networks (Wan and Lemmon,2009),machine learning (Li H et al.,2020),resource allocation (Deng et al.,2018),and so on (Yang SF et al.,2017;Shi et al.,2019;Yang T et al.,2019;Jiang et al.,2021;Wang D et al.,2021;Wang XY et al.,2021;Yue et al.,2022;Zeng et al.,2022).

Distributed optimization can be regarded as an optimization approach with a multi-agent system.Each agent has its local objective function,and a local decision variable denotes the state of an agent.The objective function of the considered optimization problem is the sum of multiple local objective functions.A distinguishing feature of distributed optimization is that the information exchange among agents is through a network topology graph.In the graph,a node denotes an agent.Each agent knows only its own information (its local objective function and local decision variable).Compared with centralized optimization,distributed optimization has several desirable features as follows: (1) each agent needs to interact with only neighbor agents,so it can save the communication cost;(2) the information related to the optimization problem is distributed and stored in each agent,so it is more private and safer;(3) there is no single point of failure,which greatly improves the fault tolerance of the system;(4) because it is a parallel computing method,the scalability of the optimization algorithm can be enhanced.

A large number of distributed optimization methods have been developed in recent years.For example,distributed subgradient methods for multiagent optimization were developed in Nedic and Ozdaglar (2009).In Liu and Wang (2015),a second-order multi-agent system was proposed for distributed optimization with bound constraints.In Zeng et al.(2017),a distributed continuous-time optimization method was presented via non-smooth analysis.In Liu et al.(2017),a recurrent neural network (RNN) system was developed for distributed optimization.Based on an RNN system,decentralized-partial-consensus constrained optimization was addressed in Xia ZC et al.(2023).In Xia ZC et al.(2021,2022),multi-complex-variable distributed optimization was studied.

Note that the proposed systems in existing works are vector-variable systems.Hence,the computation time relies on the dimension of the state in the optimization problem.However,if the dimension is high,the methods converge slowly.A matrix-valued optimization model can overcome this difficulty in several areas (Bouhamidi and Jbilou,2012;Bin and Xia,2014;Xia YS et al.,2014;Li JF et al.,2016;Huang et al.,2021).However,the results of matrix-valued optimization methods are not systematic enough,although several seminal works have been done (Huang et al.,2021;Xing et al.,2021;Zhu ZH et al.,2021;Zhang et al.,2022).

1.2 Constraints and penalty methods

Various types of constraints are studied in distributed optimization.For the resource allocation problem,the choice of each agent is in a certain range,and no agent shares its private information with others (Zeng et al.,2017).In this case,bound constraints and linear equality constraints are needed.Many engineering tasks have complex constraints due to time limitations and technical restrictions.In addition,the limitations of communication capacities cause constraints in social networks.To this end,the handling of constraints has been investigated in many works,including inequality constraints (Zhu MH and Martínez,2012;Liang et al.,2018a;Li XX et al.,2020),equality constraints (Zhu MH and Martínez,2012;Liu and Wang,2013;Liang et al.,2018b;Lv et al.,2020),bound constraints (Zeng et al.,2017;Zhou et al.,2019),and approximate constraints (Jiang et al.,2021).

The exact penalty method is a valid method for dealing with the constraints of the optimization problem.Its core is to choose feasible penalty functions and penalty gains to transform a constrained optimization problem into an equivalent unconstrained one,in which the penalty gains are not so large in contrast to the ones in the conventional penalty methods.There are several related works about the exact penalty methods for distributed optimization.An adaptive exact penalty method was proposed in Zhou et al.(2019) for distributed optimization.A distributed optimization algorithm was developed in Liang et al.(2018a) using an exact penalty function.However,Zhou et al.(2017,2019) considered the bound constraint and used the distance function as the penalty function.In this paper,we develop an exact penalty method for handling inequality and equality constraints.

1.3 Gossip model

Originating from the social communication network,the gossip model plays an important role in consensus algorithms,and is applied in sensor networks and peer-to-peer networks thanks to its advantages including high fault-tolerance and high scalability (Boyd et al.,2006).In studies of distributed optimization,the gossip model has been applied widely to achieve consensus on the states of agents.In recent years,a large number of works on gossiplike optimization algorithms have been done.For example,a gossip algorithm was designed for the convex consensus optimization in Lu et al.(2011).In Jakovetic et al.(2011),a gossip algorithm was developed to solve cooperative convex optimization in networked systems.In Yuan (2014),a gossip-based gradient-free method was developed,and the gossip model was regarded as a multi-agent system.In Koloskova et al.(2019),a distributed stochastic optimization algorithm was proposed based on a gossip model with compressed communication.

1.4 Goal and contributions

In this paper,we consider a distributed stochastic optimization problem withNagents as follows:

Problem (1) is said to be a matrix-valued distributed stochastic optimization problem.For vector-valued stochastic optimization,several works have been done.The problem of distributed stochastic optimization was addressed by Shamir and Srebro (2014).The strongly convex stochastic optimization problem was studied in Rakhlin et al.(2012).Several gossip algorithms with compressed communication were derived for decentralized stochastic optimization in Koloskova et al.(2019).

In this paper,we address the matrix-valued distributed stochastic optimization with inequality and equality constraints using an algorithm based on a gossip model.Specifically,the contributions are summarized as follows:

1.An auxiliary function is proposed to analyze several properties of the matrix-valued functions.Many common properties for vector-valued optimization methods are proposed in a matrix-valued fashion (see in Definitions 1-5 and Lemma 1).

2.A selection principle of the penalty functions and the penalty gains is derived (see in Selection principle 1).Based on the selection principle,an exact penalty method is proposed for transforming a matrix-valued optimization problem with inequality and equality constraints into a problem without inequality or equality constraints (see in Theorems 1 and 2,and Fig.1).

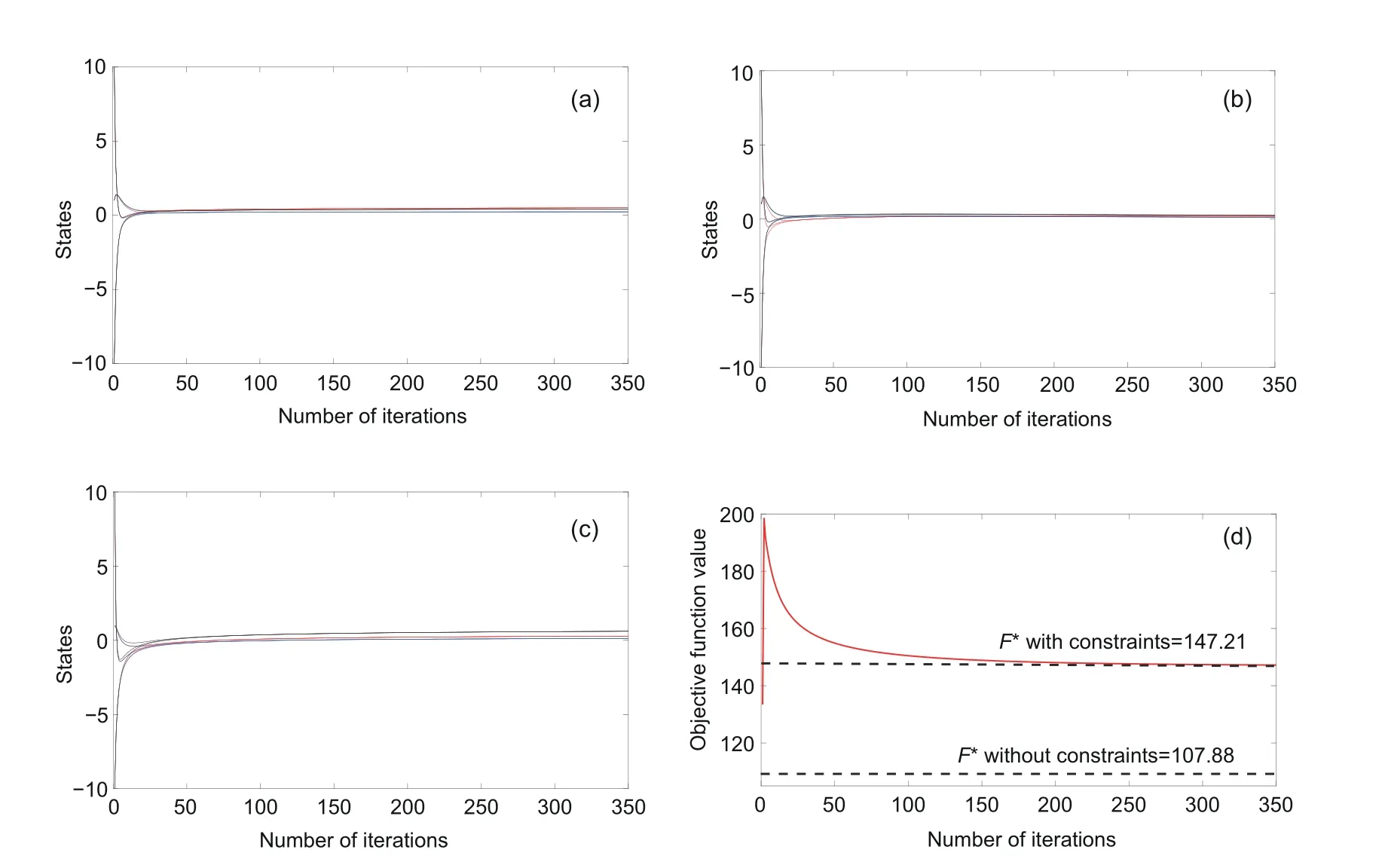
Fig.1 Transient states of Xk(1,i) (a), Xk(2,i) (b), Xk(3,i) (c),and the transient values of the objective function (d) in Example 1 (k, i ∈{1,2,3})

3.A distributed optimization algorithm based on a gossip model is developed for solving the matrixvalued distributed stochastic optimization problem (see in Algorithm 1),and its convergence is analyzed (see in Theorem 3 and Remark 1).Two numerical examples are provided to illustrate the efficiency of Algorithm 1 for solving matrix-valued distributed stochastic optimization problems (see in Figs.2 and 3).

2 Preliminaries

2.1 Notations

Let R,Rn,and Rn×mdenote the set of all real numbers,the set of alln-dimensional real vectors,and the set of all (n×m)-dimensional real matrices,respectively.IN={1,2,...,N}.‖·‖denotes the Euclidean norm,‖·‖Fdenotes the Frobenius norm,and |·|denotes the absolute value.∀X ∈Rn×m,X(i,j) denotes the (i,j)thelement ofX.vec (X)=(X(1,1),X(2,1),...,X(n,1),X(1,2),X(2,2),...,X(n,m))T∈Rnm.For vectorsx1,x2,...,xN,ATdenotes the transpose of matrixA.tr (A) denotes the trace of thenth-order matrixA.δ2(A) denotes the second largest eigenvalue of thenth-order matrixA.Indenotes then-dimensional identity matrix,and 1ndenotes then-dimensional vector with all components being 1.“⊗” denotes the Kronecker product operator.G=(V,E,A) denotes a graph withNnodes,whereV=INis the node set,E ⊂V×Vis the edge set,andA ∈RN×Nis the weighted adjacency matrix.A(i,j) >0 if (i,j)∈E;otherwise,A(i,j)=0.LetNi={j|A(i,j)/=0}be the set of the neighbors of nodei.For a setS ⊂Rn×m,PS(X)=arg minY∈S‖X-Y‖F.

2.2 Matrix-valued function

In problem (1),local objective functionfiis a mapping from Rn×mto R.In addition,the functionsgandhin the constraints are the mappings from Rn×mto R.In this study,we call the functionf: Rn×m →R a matrix-valued function.An optimization problem is said to be a matrix-valued optimization problem if its objective function is a matrix-valued function withn/=1 andm/=1.Different from the normal vector-valued optimization,the decision variable of a matrix-valued optimization problem is a matrix.

To address matrix-valued optimization problem (1),we need to analyze the properties of matrix-valued functionf.Before analyzing the properties off,we define an auxiliary functionα(x)=f(X),wherex=vec (X).α(x) is a useful tool for proving the properties off(X).Now,we propose several definitions and lemmas off(X) usingα(x).

Definition 1(L-Lipschitz continuity)f:Rn×m →R is said to beL-Lipschitz continuous if∀X,Y ∈Rn×m,∃L>0,such that |f(X)-f(Y)|≤L||X-Y‖F,whereLis a Lipschitz constant.

Definition 2(l-smoothness)f:Rn×m →R is said to bel-smooth if∀X,Y ∈Rn×m,∃l>0,such that‖∇f(X)-∇f(Y)‖F≤l||X-Y‖F.

Definition 3(μ-strong convexity)f: Rn×m →R is said to beμ-strongly convex if∀X,Y ∈Rn×m,∃μ>0,such thatf(Y)≥f(X)+tr ((∇f(X))T(YX))+μ‖Y-X/2.

Note that Definition 3 defines the convexity offifμ=0.

Definition 4For any convex functionf:Rn×m →R,the subdifferential offwith respect toXis defined by

In addition,G ∈∂f(X) is called a subgradient offatX.

Furthermore,based on the properties of the Frobenius norm and Definitions 1-3,two lemmas are derived:

Lemma 1Assumef:Rn×m →R andα:Rnm →R with vec (X)=x.∀X,Y ∈Rn×m,we have the following statements:

(4)f(X) isl-Lipschitz continuous if and only ifα(x) isl-Lipschitz continuous;

(5)f(X) isl-smooth if and only ifα(x) islsmooth;

(6)f(X) isμ-strongly convex if and only ifα(x) isμ-strongly convex.

ProofFor statement (1),we can obtain

For statement (3),it is a well-known norm inequality.For statements (4)-(6),they can be easily proved using statements (1) and (2).

Lemma 2Iff(X) isμ-strongly convex and bounded withM′,and∇f(X) is bounded withM′′,thenf(X) is 2M′μ/M′′-Lipschitz continuous.

ProofBased on statement (5) in Lemma 1,α(x) isμ-strongly convex iff(X) isμ-strongly convex.Then,according to Lemma 4.2 in Zhou et al.(2017),we have thatα(x) is 2M′μ/M′′-Lipschitz continuous.Based on statement (3) in Lemma 1,f(X) is 2M′μ/M′′-Lipschitz continuous ifα(x) is 2M′μ/M′′-Lipschitz continuous.

Definitions 1-3 provide several properties of functionf(X) which will be commonly considered in the vector-optimization theory.Thus,in matrixvalued optimization,we generalize them into the matrix-valued domain.Based on Lemma 1 andα(x),many existing results in the vector-valued domain Rnmcan be generalized to the matrix-valued domain Rn×m.For example,Lemma 2 can be proved via statements (4) and (6) in Lemma 1.According to Lemma 2,the strong convexity can lead to Lipschitz continuity under the conditions in Lemma 2.

For a non-smooth function,the subgradient defined in Definition 4 is adopted when the gradient does not exist.In distributed optimization,there are many works about non-smooth analysis with subgradients (Ruszczyński,2006;Zeng et al.,2017).In the optimization problem minif for anyi ∈IN,fi(Xi) satisfies the Lipschitz condition in Definition 1,the sum sign and the subdifferential sign can be exchanged,i.e.,This statement can be proved by changing the matrix problem into a vector problem via functionα(x),and its proof can be obtained from Ruszczyński (2006) by statement (3) in Lemma 1.In addition,for Definitions 2 and 3,if the function is non-smooth,we can substitute its subgradient for its gradient.In these cases,μ-strong convexity is still calledμ-strong convexity,butl-smoothness is now calledl-pseudo smoothness and is defined as follows:

Lemma 3 provides a sufficient condition for judging thel-pseudo smoothness of a non-smooth function.

3 Problem formulation

Consider an optimization problem with inequality and equality constraints as follows:

Problem (2) is a constrained matrix-valued distributed optimization problem,and the handling of its constraints is a difficult point.For handling bound constraints,a penalty method was proposed in Zhou et al.(2019).In Zhou et al.(2019),the selection of penalty gains relied on the Lipschitz constants of the objective functions,and the continuoustime optimization method was also dependent on the penalty gains.Compared with bound constraints,equality and inequality constraints in problem (2) are more complex,and the selection of penalty gains relies on not only the objective functionsfi,but alsogandh,which may be more complex than the optimization in Zhou et al.(2019).Thus,we will develop an exact penalty method for handling the equality and inequality constraints in Section 4.2.The exact penalty method can transform an optimization problem with equality and inequality constraints into an optimization problem without equality or inequality constraints.

Using the penalty method,an optimization problem without inequality constraintg(Xi)≤0 or equality constrainth(Xi)=0 is proposed as follows:

The core of the penalty method is to derive feasible penalty gains and penalty functions for guaranteeing the equivalence between the original constrained problems and unconstrained problems.In this study,AiandBiare penalty functions.PgiandPhi(i=1,2,...,N) are the penalty gains that need to be chosen to guarantee the equivalence between problems (2) and (3).Thus,the penalty gainsPgiandPhiare important for problem transformation,and the selection principle of them is given in Section 4.1.

In addition,we propose a new type of optimization,matrix-valued distributed stochastic optimization,in which stochastic variables are considered into problem (2),and its form is shown as follows:

Note that problems (4) and (1) are identical if we setXi=Xj=X,∀i,j ∈IN.Fi(Xi,ξi) can be regarded as a stochastic function sinceDisatisfies some distribution.We call problem (4) a matrixvalued distributed stochastic optimization with inequality and equality constraints.In this study,we focus on solving problem (4) by developing a distributed optimization algorithm.

4 Main results

In this section,we address the exact penalty method and the development of a distributed optimization algorithm for solving the matrix-valued distributed stochastic optimization problem (4).In Section 4.1,a selection principle of penalty gains and penalty functions is proposed.Then,we analyze how to obtain feasible penalty gains.In Section 4.2,an exact penalty method is proposed to select the penalty gains and handle the inequality and equality constraints.In Section 4.3,an algorithm based on a gossip model for solving problem (4) is developed.

4.1 Selection principle of penalty gains

Beginning with a centralized matrix-valued optimization problem minf(X) s.t.X ∈S ⊂Rn×m(Sdenotes a feasible set),we propose a selection principle for seeking the penalty gains and penalty functions:

Selection principle 1Penalty gainc(c>0) and penalty functionτS(X) : Rn×m →R satisfy the following conditions:

(1)∀X ∈Rn×m,f(X)+cτS(X)≥f(PS(X));

(2)∀X ∈Rn×m,τS(X)≥0;

(3)∀X ∈S,τS(X)=0.

Based on Selection principle 1,the equivalence theorem is derived in the following:

Theorem 1If there existcandτS(X) satisfying Selection principle 1 and the considered problem has at least one solution,then arg minX∈S f(X)=arg minX∈Rn×m(f(X)+cτS(X)).

According to Theorem 1,if the penalty functionτS(X) and the penalty gaincsatisfy Selection principle 1,then the equivalence between the original constrained problem minX∈S f(X) and problem minX∈Rn×m(f(X)+cτS(X)) can be guaranteed.Similarly,we can select the penalty functions and penalty gains by Selection principle 1 to guarantee the equivalence between problems (2) and (3).Actually,when we setS:=Ωgi={Xi|g(Xi)≤0},the function

satisfies conditions (2) and (3) in Selection principle 1.When we setS:=Ωhi={Xi|h(Xi)=0},the function

satisfies conditions (2) and (3) in Selection principle 1.Hence,if the penalty gainsPgiandPhisatisfy condition (1) in Selection principle 1,then problems (2) and (3) are equivalent.Therefore,in the next subsection,we propose an exact penalty method to select feasible penalty gains satisfying condition (1) in Selection principle 1.

4.2 A penalty method

In this subsection,we derive the selection of penalty gains for problem (2).Let

Then,Assumption 1 is provided as follows:

Assumption 1(1)fiis convex andLf-Lipschitz continuous fori ∈IN;(2) Slater’s condition holds.

Next,we give the equivalence theorem between problems (2) and (3) on the basis of penalty gainsPgiandPhisatisfying the conditions withLgi(Xi) andLhi(Xi):

Theorem 2Under Assumption 1,ifLgi(Xi)Pgi+Lhi(Xi)Phi ≥LfforXi/∈Ωgi ∩Ωhi,then problem (2) is equivalent to problem (3).

4.3 Matrix-valued distributed stochastic optimization algorithm based on a gossip model

In this subsection,we develop an algorithm based on a gossip model (its vector-valued form can be found in Xiao and Boyd (2004)).First,we introduce the gossip model as follows:

wherei ∈IN.κ>0 limits the rate of the gossip updating.Each stateXiis ann×mmatrix.Ais the adjacency matrix of graphG=(V,E,A).In gossip updating,each agent shares its own information with its neighbors and updates by local average,which makes all of the agents reach an agreement on a target solution.

Before proceeding,we propose Assumption 2:

Assumption 2(1)fiis bounded withm,μstrongly convex,andl-smooth fori ∈ IN.∇fiis bounded withM.(2)Aiis convex andlg-pseudo smooth;Biis convex andlhpseudo smooth.∂Aiis bounded withMg,and∂Biis bounded withMh.(3) Fori ∈ IN,withσiandEbeing known upper bounds.(4)Ais a symmetric doubly stochastic matrix.(5) Slater’s condition holds.

In Assumption 2,the convexity of the objective functions and constraint functions can lead to a globally optimal solution for optimization problems (Boyd and Vandenberghe,2004) when the optimal solution exists.The strong convexity and thel-smoothness contribute to the proof of the convergence of the proposed algorithm (Rakhlin et al.,2012).According to Lemma 2,item (3) gives the characteristics of random sampling.Item (4) indicates that the graph is connected and weightbalanced,which contributes to the consensus of states.Slater’s condition is a common constraint qualification to guarantee the solvability of an optimization problem (Liu et al.,2017;Xia ZC et al.,2022).

To proceed,based on the gossip model,Algorithm 1 is developed for solving problem (4).

Xiis regarded as the state of theithagent.Eqs.(5) and (6) are regarded as information update processes of theithagent,and they originate from the gossip model.Each agent shares its own information with its neighbors byAand updates by local average,which makes all of the agents reach an agreement on a target solution.Therefore,Eq.(5) with Eq.(6) is a multi-agent system,and Algorithm 1 is a distributed optimization method.

In Algorithm 1,the time-varying stepζ(k) should be chosen to achieve convergence to the optimal value.Thus,we give a convergence theorem to prove the convergence of Algorithm 1,andζ(k) is designed in the theorem.Before proposing the convergence theorem,we introduce four necessary lemmas.

Based on Eq.(8),the proof of Lemma 4 is completed.

According to Lemma 2,we have thatfiis 2mμ/M-Lipschitz continuous.

Lemma 5Assume thatX∗is an optimal solution to problem (4).Under Assumption 2,(k) in Algorithm 1 satisfies

Based on item (4) in Assumption 2,we can derive

Then,according to statement (3) in Lemma 1,and items (1) and (2) in Assumption 2,we have

According to items (1) and (2) in Assumption 2,we can also obtain

Combining with expressions (10)-(12),the proof is completed.

Lemma 6(Koloskova et al.,2019) Under Assumption 2,{X(k)}k≥0in Algorithm 1 withζ(k)=a1/(k+a2),a1>0,anda2≥5/psatisfies

From Theorem 1 in Koloskova et al.(2019),we obtainp=κ(1-δ2(A))(κis from the gossip model).Based on item (4) in Assumption 2,Ais a symmetric doubly stochastic matrix;thus,all its eigenvalues are positive and its largest eigenvalue is 1.

Lemma 7(Koloskova et al.,2019) Let{a(k)}k≥0witha(k)≥0 and{e(k)}k≥0withe(k)≥0 be the sequences satisfying

Summing with Lemmas 4-7,we derive a theorem as follows,which implies that Algorithm 1 can converge to an optimal solution to problem (4) with a properζ(k):

Theorem 3Under Assumption 2,forp>0,Algorithm 1 forζ(k)=4/(χ1(a+k)) witha ≥5/pconverges at the rate

ProofSubstituting inequality (13) into the bound in inequality (9),we can obtain

Theorem 3 provides the proper time-varying stepζ(k) for Algorithm 1.Withζ(k),Algorithm 1 can solve the matrix-valued distributed stochastic optimization problem (4).In the next section,we will provide two examples to show the validity of the proposed penalty method and Algorithm 1.

Remark 1(Convergence rate) The convergence rate of Algorithm 1 is(see in Theorem 3),whereχ1=μandχ2=2M2+4PgMg+4PhMh.The methods developed in Zhou et al.(2019),Huang et al.(2021),Xia ZC et al.(2021),and Zhang et al.(2022) are continuous-time optimization methods;thus,they are conservative.Therefore,their convergence rate is low.The convergence rate of the algorithm in Koloskova et al.(2019) isBecause the problems considered in Koloskova et al.(2019) are not subject to any constraint,T1(K) is larger thanT2(K).The extra part ofT1(K),exceptT2(K),is the handling of constraints;note thatχ2,with respect to constraints mainly,is natural to the balance between unconstrained problems and constrained ones.

Remark 2(Complexity) The numbers of floating points are the same inXand vec (X).Thus,the spatial complexities of a matrix-valued algorithm and a vector-valued algorithm are the same when there are no other constraints.The complexity of Algorithm 1 isO(4KN(nm+1)),while the complexity of the algorithm in Koloskova et al.(2019) isO(3KNnm).The difference is also generated from the handling of constraints naturally.

Compared with conventional distributed optimization methods (see in the references in Section 1.1),we consider matrix-valued optimization and stochastic optimization.In addition,an exact penalty for dealing with (in) equality constraints is employed to distributed optimization.Table 1 presents the comparison results.

Table 1 Comparison of existing works with this study

5 Simulations

In this section,two numerical examples are presented to illustrate the characteristics of the penalty methods and Algorithm 1.The algorithm and the data are implemented and simulated in MATLABⓇR2017b and run on IntelⓇCoreTMi5-8257U CPU@1.40 GHz,Intel Iris Plus Graphics 645 1536 MB,8 GB 2133 MHz LPDDR3,macOS 10.15.7.

Example 1Consider the following matrix-valued distributed optimization problem withN=3:

Note that the objective functions are all convex and-strongly convex.The equality constraint function and inequality constraint function are linear.Thus,the penalty functionsA(X) andB(X) are convex and pseudo smooth.We can obtain the optimal solutionwithout any constraint as follows:

and the optimal value 107.88.Then,we perform Algorithm 1 without random samples where parameters are taken asκ=0.1,Pg=4,Ph=10,

withδ2(A)=0.8212,anda=280 based onp=0.0178.

Based on MATLAB,we run Algorithm 1,and we can obtain Figs.1a-1c depicting the transient states ofXk(i,j),k,i,j ∈{1,2,3},showing that Algorithm 1 is always globally convergent.We can obtain the optimal solution to problem (14):

and the optimal value is 147.21.Fig.1d shows that the objective function value obtained by Algorithm 1 is the same as the optimal solution to problem (14).Therefore,the exact penalty method is valid,and Algorithm 1 can solve problem (14) without random samples.

Then we add random samples to problem (14),and other settings remain the same.We run Algorithm 1 by MATLAB and Fig.2 is obtained.Fig.2 depicts the transient objective function values of problem (14) with or without random samples by running Algorithm 1.Note that two trajectories are roughly the same;thus,Algorithm 1 can also solve problem (14) with random samples,which illustrates that Algorithm 1 can be used to solve matrix-valued distributed stochastic optimization problems.

Fig.2 Transient values of the objective function in Example 1

Example 2Consider a matrix-valued distributed stochastic optimization problem with more agents and higher dimensions (N=10 andX ∈R9×9) as follows:

We run Algorithm 1 to solve problem (15) without or with random samples,and then we obtain Fig.3.Fig.3 shows the errors between the transient values of the objective function obtained by Algorithm 1 and the optimal values of the objective function in Example 2.The error converges to 0,and two trajectories are roughly the same,which illustrates the validity of Algorithm 1.

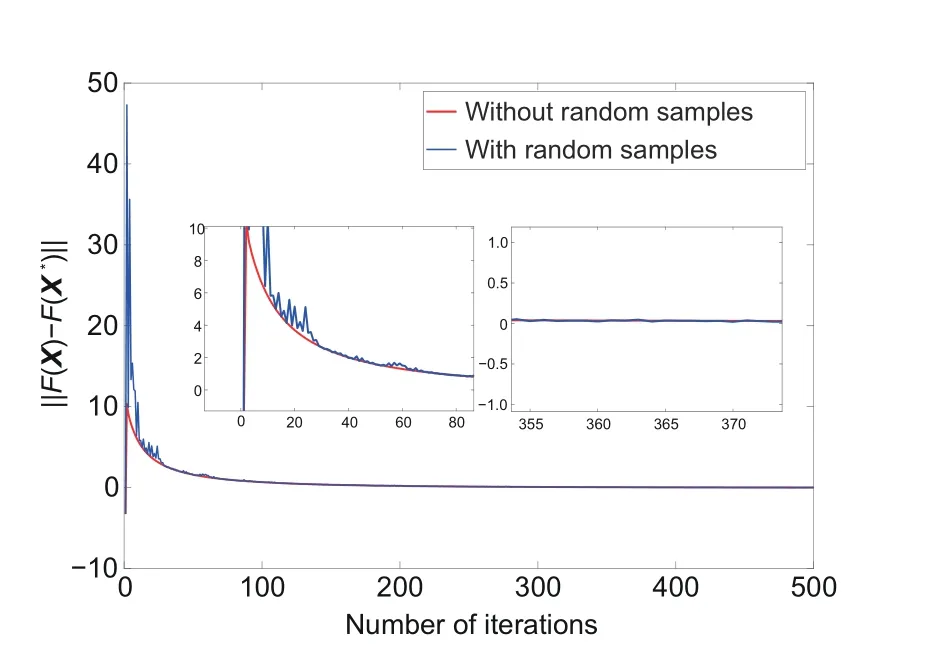
Fig.3 Errors between the transient values of the objective function obtained by Algorithm 1 and the optimal values of the objective function in Example 2

6 Conclusions

In this paper,we have focused on a special constrained optimization called matrix-valued distributed stochastic optimization subject to inequality and equality constraints.We have adopted an exact penalty for the handling of the constraints.Based on a gossip model,we have developed a distributed stochastic gradient descent algorithm and analyzed its stability.Two illustrative examples have been provided to explain the validity of the exact penalty method and the optimization method.

Contributors

Zicong XIA,Yang LIU,and Wenlian LU designed the research.Zicong XIA processed the data.Zicong XIA and Yang LIU drafted the paper.Wenlian LU and Weihua GUI helped organize the paper.Yang LIU and Weihua GUI revised and finalized the paper.

Compliance with ethics guidelines

Yang LIU is a guest editor of this special feature,and he was not involved with the peer review process of this manuscript.Zicong XIA,Yang LIU,Wenlian LU,and Weihua GUI declare that they have no conflict of interest.

Data availability

The data that support the findings of this study are available from the corresponding author upon reasonable request.