数学问题解答

(山东省临清市北门里街颐清园小区19号楼7单元2楼西户 刘继征 252600)

(山东省邹平双语学校 姜坤崇 256200)

(山东省泰安市宁阳县第一中学 刘才华 271400)

(安徽省无为中学 朱小扣 238300)

(北京中学 史嘉 100028)

(陕西省咸阳师范学院教育科学学院 安振平 712000)

(山西省临县一中 李有贵 033200)

(广东省中山纪念中学 邓启龙 528454 )

(江苏省兴化市教师发展中心教研室 张俊 225700)

(天津港职工培训中心 黄兆麟 300456)

2023年6月号问题解答

(解答由问题提供人给出)

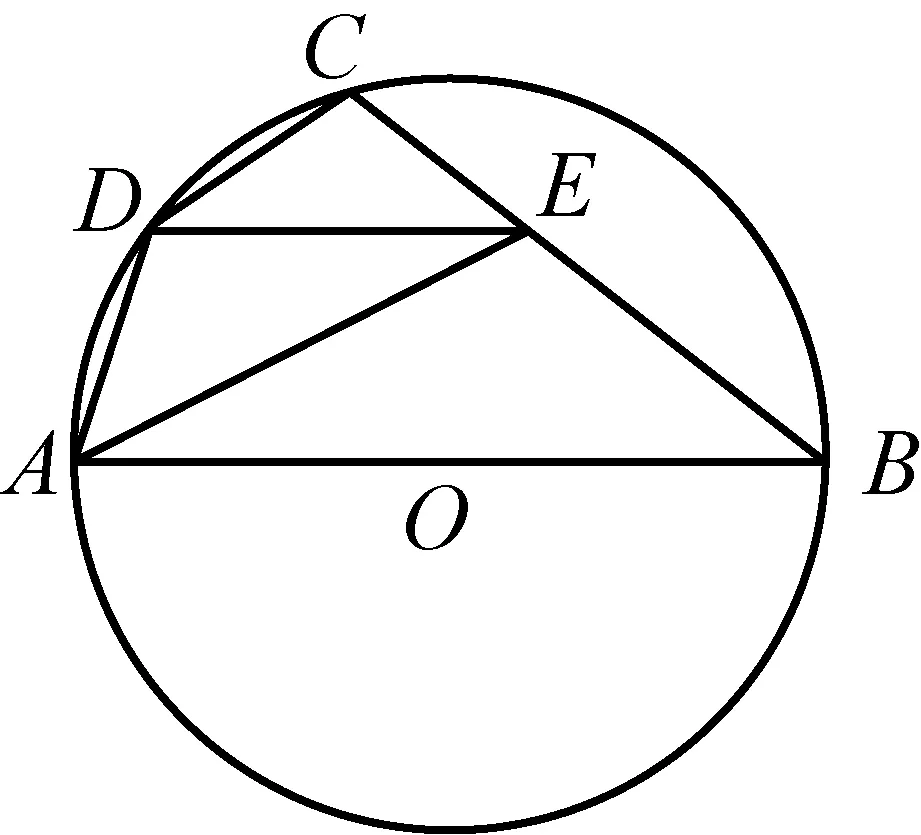
(山东省临清市北门里街颐清园小区19号楼7单元2楼西户 刘继征 252600)

解连接AC、BD、OD,并作EF⊥AB、DG⊥AB,

垂足分别是点F、点G,

因为AB是⊙O的直径,

所以∠ACB=∠ADB=90°,

所以AD=CD=12,OD⊥AC,

所以OD∥BC,又因为DE∥AB,

因此,四边形OBED是平行四边形,

又OB=OD,所以平行四边形OBED是菱形.

由DE∥AB,以及EF⊥AB、DG⊥AB,

可知四边形DEFG为矩形.

在Rt△ABD中,由勾股定理得

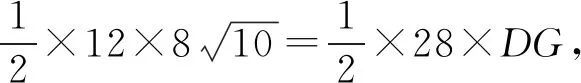
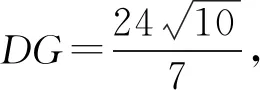
又在Rt△BEF中,由勾股定理得

所以在Rt△AEF中,由勾股定理得

2727设n∈N+且n≥3,k∈N+,求证:

nn+k>(n+k)n.

(山东省邹平双语学校 姜坤崇 256200)

证明对k(k≥1)用数学归纳法.

(1)当k=1时,即证nn+1>(n+1)n.

因为n≥3,所以(n-1)2>2,即n2-2n-1>0,

所以nn+1>(n+1)n.

(2)假设当k=m(m≥1)时所证不等式成立,

即nn+m>(n+m)n,则当k=m+1时,

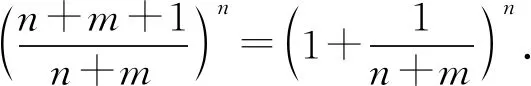
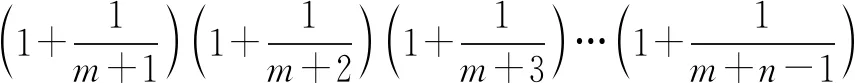
所以由归纳假设及以上不等式得

nn+m+1=nn+m·n>(n+m)n·n>(n+m+1)n,

即nn+m+1>(n+m+1)n,此不等式表明,当k=m+1时所证不等式也成立.

综合(1)、(2)知,所证不等式对一切自然数k(k≥1)都成立.

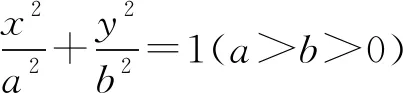
(山东省泰安市宁阳县第一中学 刘才华 271400)

由题意得A(0,b),B(0,-b).直线PA的方程为

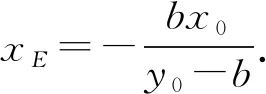
设过P的切线方程为y-y0=k(x-x0),

直线PM的方程为y-y0=k1(x-x0),

直线PN的方程为y-y0=k2(x-x0).

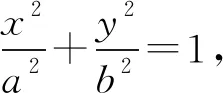
(a2k2+b2)x2+2k(y0-kx0)a2x+a2(y0-kx0)2-a2b2=0.

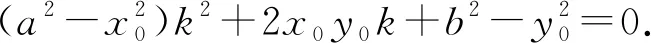
由题意知上述方程是关于k的一元二次方程,

方程有两个不同实根k1,k2,且

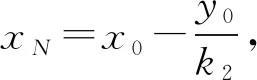
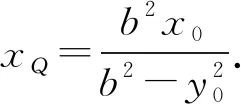
(安徽省无为中学 朱小扣 238300)

解

得(x+y+z)2=t2+36,

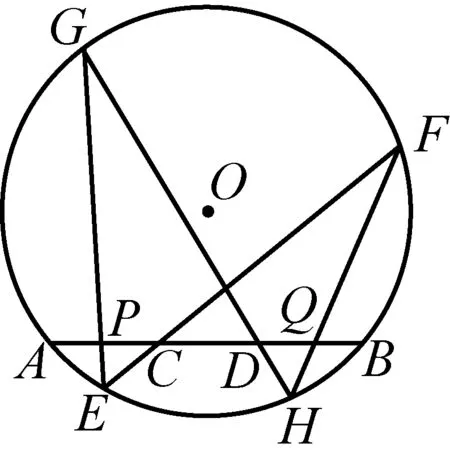
2730如图,已知C,D是⊙O的弦AB上的两点,满足AC=BD.过点C,D分别作⊙O的两条弦EF,GH,连接GE,FH分别交AB于点P,Q.求证:PC=QD.

(北京中学 史嘉 100028)

证明如图,过点G作GG′∥AB交⊙O于点G′,连接CG′,QG′,FG′.

根据GG′∥AB,AC=BD和圆的对称性知

∠GG′C=∠G′CD=∠GDC=∠G′GD,

GD=CG′.

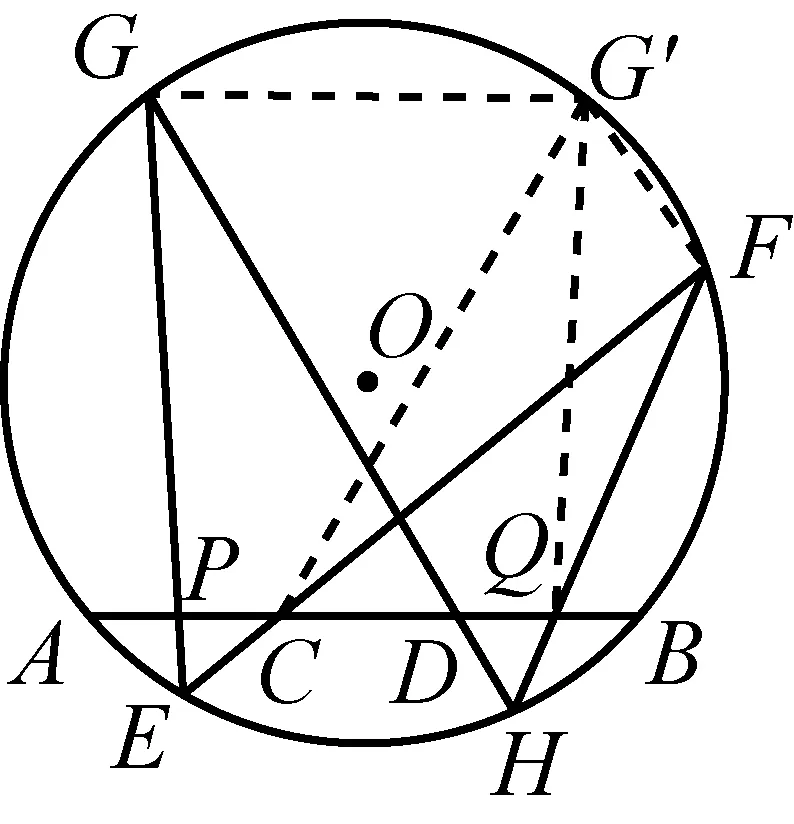
由G,G′,F,H四点共圆知

∠G′GH+∠G′FH=π,

所以∠G′CQ+∠G′FQ

=∠G′CD+∠G′FH=π,

即G′,C,Q,F四点共圆,

所以∠CG′Q=∠CFQ.

由E,G,F,H四点共圆知

∠EGH=∠EFH,

所以∠EGH=∠CG′Q.

综上知△GPD≌△G′QC,则PD=QC,

所以PD-CD=QC-CD,即PC=QD.

2023年7月号问题

(来稿请注明出处——编者)

2731在△ABC中,求证:

(陕西省咸阳师范学院教育科学学院 安振平 712000)

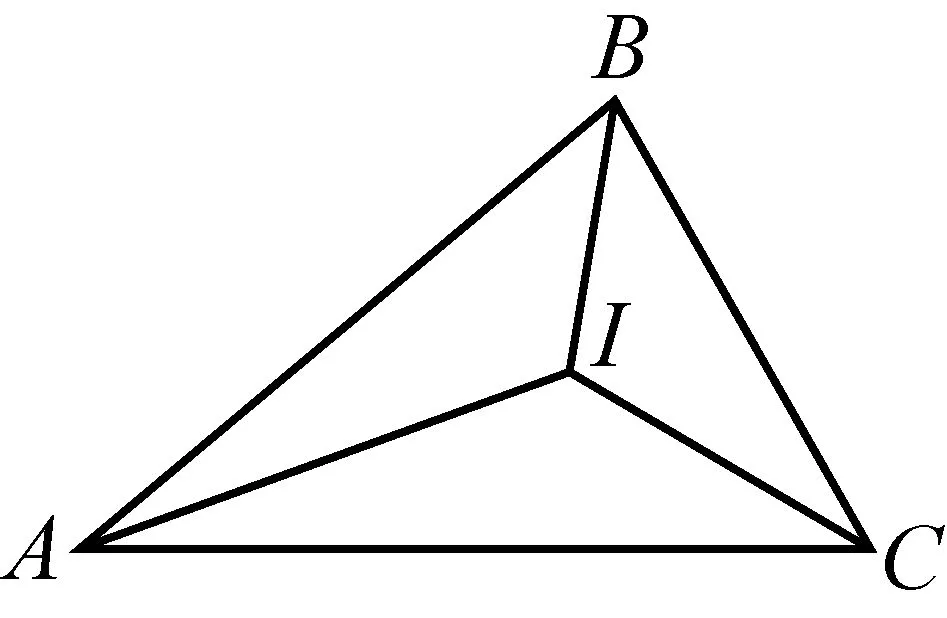
2732在△ABC中,角A,B,C的对边分别为a,b,c,AI,BI分别平分∠BAC,∠ABC,且∠ACB=60°,∠ABC=2∠BAC,求证:CI2=a2+c2-b2.

(山西省临县一中 李有贵 033200)

2733设a,b,c>0,且a+b+c=1,证明:

(1+a)(1+b)(1+c)

(广东省中山纪念中学 邓启龙 528454 )

(江苏省兴化市教师发展中心教研室 张俊 225700)

2735设△ABC的三条边,三个旁切圆半径,三条高线,面积和半周长分别为a,b,c,ra,rb,rc,ha,hb,hc,Δ,p,则

(天津港职工培训中心 黄兆麟 300456)