重载交通作用下桥梁结构承载能力研究

王 超

（广东冠粤路桥有限公司,广东 广州 510000）

0 引言

桥梁结构在承受超极限的车辆荷载作用时，稳定性和耐久性均下降，安全隐患激增。出于安全考虑，该文建立有限元模型，模拟分析桥梁在不同超载货车通行时的受力特性，评估桥梁使用过程中在各工况下的安全状况，掌握桥梁的具体特点，在此基础上针对性地采取桥梁安全防护措施[1]。相比以标准车型、标准荷载为依据的模拟方法，有限元模型建模分析方法获得的结果更加全面与科学，可行性较高，具有探讨的必要。

1 公路桥梁承载能力检测概述

经实物调查、荷载实验、分析计算后，确定桥梁结构的动力特性，综合考虑桥梁在各工况下的实际使用情况，检验桥梁的承载能力，根据检验结果采取加强防护措施，保证城市桥梁的安全使用[2]。城市桥梁承载能力的检测项目包含结构的强度、刚度、结构是否存在裂缝或其他形式的病害、地基和基础等，经过全方位检测后，全面汇总检测结果，对桥梁承载能力做客观的判断[3]。

2 公路桥梁结构承载能力检测的目的

桥梁建设规模持续扩大，一系列新型桥梁应运而生，桥梁总体施工水平有所进步，但桥梁建设较为复杂，存在诸多对工程质量造成影响的因素，可能导致桥梁建成后难以安全使用。同时，社会经济良好发展，道路车流量增加，车辆重载化趋势明显，部分既有桥梁难以承受日益增加的车辆荷载作用[4]。为掌握桥梁的使用效果，需要进行桥梁检测，根据检测结果评价桥梁的质量，其中承载力则属于重要的检测项目。经过桥梁承载力检测后，获得的检测结果可作为竣工验收的依据，同时也能够从中总结技术经验，持续提高桥梁的建设水平。对于正处于使用阶段的桥梁，经过承载力检测后，可评价桥梁的承载能力以及使用状况，确定桥梁结构的安全储备，判断桥梁在不同工况下的具体表现，根据检测结果主动采取防控措施，以免出现严重的质量问题或安全事故。对于有明显损伤的桥梁、存在特种荷载作用的桥梁、需提高结构承载力的桥梁、技术资料缺失的桥梁以及运营条件出现明显变化的桥梁，均可进行承载力检测，产生的检测结果对工程施工活动和管理活动的开展有重要的指导作用[5]。

3 桥梁有限元模型的构建及可行性分析

以漠阳江特大桥为例，进行桥梁有限元模型的建立并对其可行性进行分析。桥梁位于阳江市江城区，为公路Ⅰ-级的箱梁桥，桥址区地势较为平坦，上部采用装配式预应力混凝土小箱梁和预应力混凝土连续箱梁，下部为实体墩和柱式墩。

桥梁有限元模型的建立采用Midas FEANX 软件，主梁单元类型为实体单元。桥梁整体截面高度较小，桥面铺装层对主梁惯性矩产生影响，在建模时要考虑桥面铺装的作用；暂不考虑沥青磨耗层的影响，将桥梁顶板和铺装层视为整体结构进行建模；主梁的翼缘板与箱梁的现浇接缝的连接刚度较大，建模时将两者视为整体。对桥梁实体结构做精细化模拟。在建立实体有限元模型后，用Midas Civil 软件建立梁格模型进行检验，判断其是否具有可行性。

在梁格法模型和实体有限元模型的不同位置施加相同荷载，判断各板（梁）是否存在位移以及存在位移时的具体程度，对比分析后评价两者的相似程度，判断梁格法模型的可行性。

加载工况考虑如下2 种：

工况1：在3#梁跨中施加1 000 kN 的集中力，即中载作用。

工况2：在1#梁跨中施加1 000 kN 的集中力，即偏载作用。

在确定2 种加载工况后，进行建模分析。每片梁在两种模型中的位移对比结果如图1 所示。

图1 两种模型的位移对比图

根据位移曲线可掌握模型的位移变化特点，对比分析发现两者具有较高的一致性，两种工况下的位移误差均不超过5%。由此表明，梁格法模型的可行性较高，可针对此模型做进一步的分析。

4 重载交通作用下的桥梁荷载效应

以桥梁关键截面的内力效应为主要的分析对象，研究不同荷载条件下各梁的内力效应。

每片板（梁）支座处的剪应力效应、跨中的位移效应及正弯矩效应等均采用Matlab 批量化计算的方法，经过计算后，根据计算结果绘制时程曲线图，如图2 所示。板（梁）在重载时的最不利响应则对应的是时程曲线的峰值，因此可根据时程曲线确定板（梁）在重载时的最不利响应。经过对特征响应的分析后，评价重车荷载作用下桥梁结构的空间响应特征。以该工程的标准桥型梁桥为例，其结构响应特征值如图3 所示。分析发现，桥梁结构的空间响应水平随着桥梁跨径的增加而加大，但无论桥梁跨径如何变化，桥梁结构响应特征的变化趋势并不会因此而发生改变。

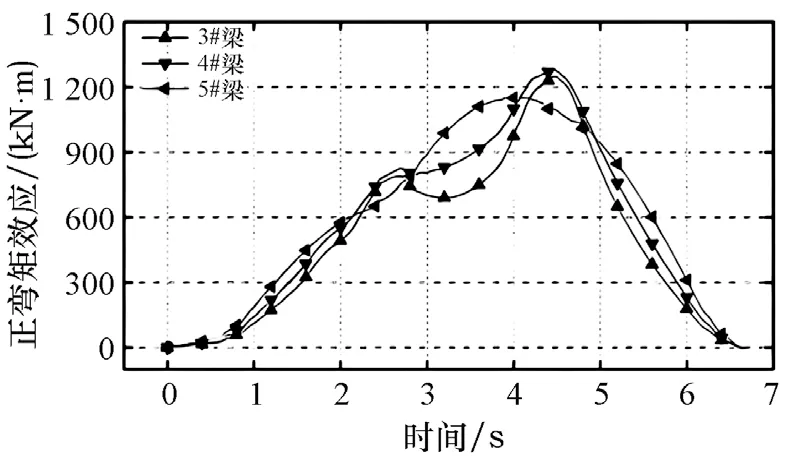
图2 正弯矩响应时程曲线

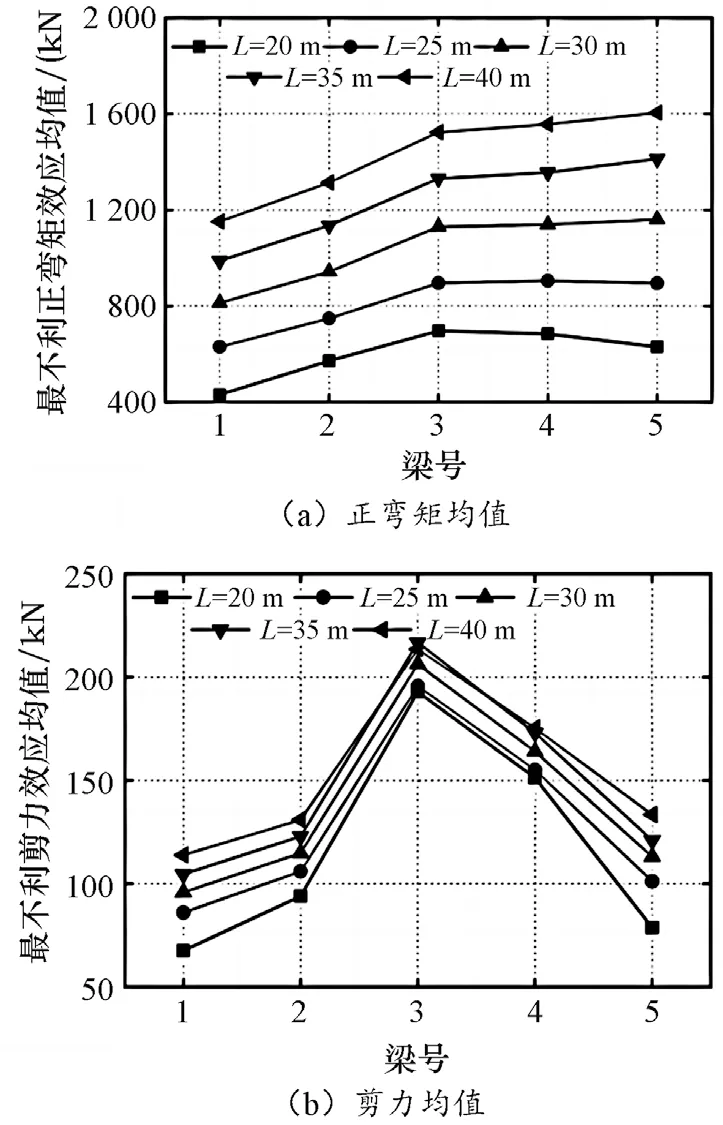
图3 不同跨径下桥梁空间结构响应特征值

5 桥梁结构承载能力响应特征

在分析重车荷载作用下桥梁各片板（梁）的效应特征时，分析对象着重考虑正弯矩效应和剪力效应。标准桥型的各片板（梁）的最不利正弯矩响应和最不利剪应力响应的计算结果，如表1、表2 所示。

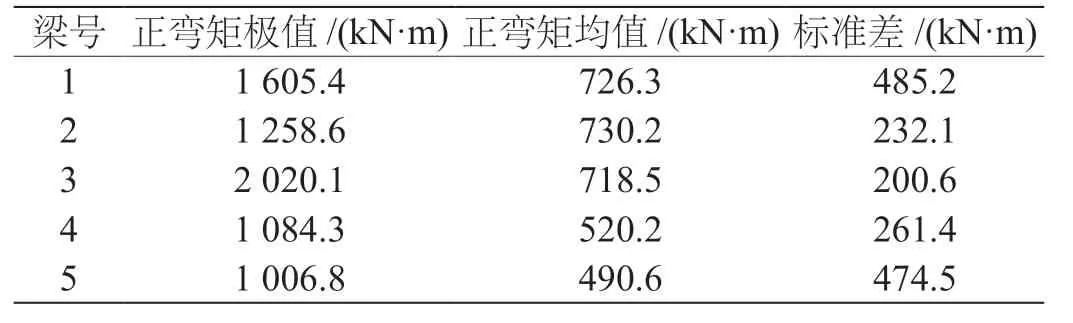
表1 桥梁结构正弯矩效应响应特征分析

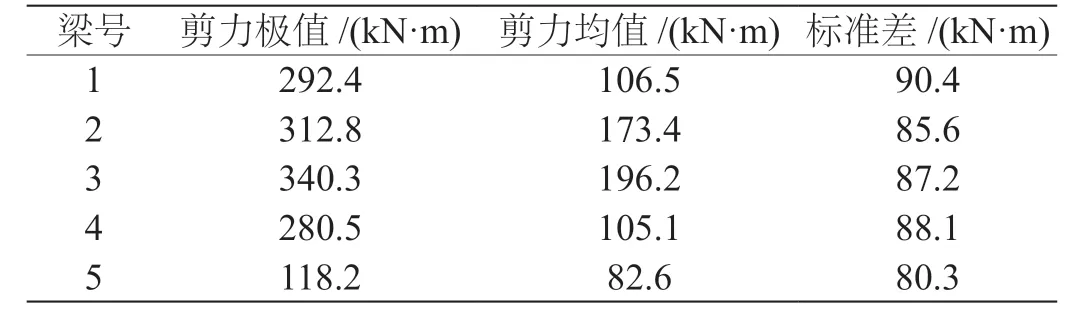
表2 桥梁结构剪力效应响应特征分析

6 重载交通作用下桥梁结构的抗弯承载能力

承载能力分析时考虑的工况是桥梁一般服役状态及重载交通作用，涉及的指标为关键截面的荷载效应组合与正弯矩效应的抗力值，根据两项指标评价桥梁承载能力安全性。桥梁结构在重车通过时的结构安全评价指标，如下：

式中，RGik——恒载效应，λGi=1.2；RQ1k——汽车荷载效应；RQjk（j≥2）——其他可变荷载效应（除汽车荷载效应外），λQj=1.4；根据RQjk（j≥2）的数量予以确定，P——桥梁结构抗力。

在前述提及的公式（1）中，重车通过时桥梁结构的最大弯矩效应属于整个公式中的唯一变量，结构的恒载效应、温差效应等均视为常量处理。对于重车荷载作用下不同跨径桥梁的弯矩承载能力，此指标的极值和均值均呈一定程度的波动，但从影响机制的角度来看，此变化与桥梁跨径无关。以重车荷载作用下的连续箱梁为例，弯矩承载能力的均值约为0.58，极值在1.0 以内，由此可以确定的是桥梁结构的极限承载能力在重车荷载作用之上，即重车荷载的作用在桥梁可承受的范围内。

7 桥梁车辆限载问题的处理

桥梁车辆超限相关问题的分析采用的是可靠度理论，在分析全过程中，建立极限状态方程属于重要内容，其中主要随机变量的分布类型及参数对方程建立状况产生明显的影响，因此合理选择随机变量的分布类型及参数至关重要。此外，还需根据目标可靠指标反推重车荷载分布，再进一步视荷载分布条件确定正弯矩效应的范围。在进行桥梁车辆超限问题的分析时，随机变量主要考虑的是结构自身抗力、荷载作用效应和重车荷载效应。按照前述描述的思路，建立极限状态方程如下：

式中，R——结构抗力；G——恒载效应；Q——重车荷载作用；m——其他荷载效应。

正弯矩效应阈值取正弯矩效应分布的均值，即0.2~0.7，控制变量为变化梯度为0.1 的变异系数。经过计算，确定正弯矩效应阈值，具体如图4 所示。

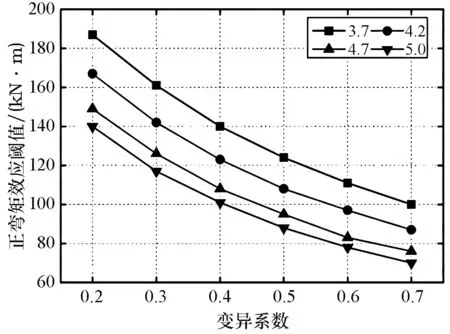
图4 不同变异系数对应的正弯矩效应阈值

根据图4 可知，变异系数的增加将带来正弯矩效应阈值的下降，且呈现出明显降低的变化趋势，可见不同变异系数所带来的计算结果不尽相同，变异系数属于对计算结果造成影响的关键因素，合理选取变异系数至关重要。根据综合性和全面性的要求予以选择，在保证变异系数的合理性后，有助于获得准确可靠的计算结果。

8 结语

综上所述，在该文的研究中，利用空间梁格法建立桥梁结构有限元模型，将其与实体有限元模型加以对比，评价模型的可行性以及该建模方法的适用性。研究过程中，在建立梁格有限元模型后，用Midas 计算桥梁板（梁）的空间响应特征及其他相关参数，进而从桥梁内力、结构承载性能、抗裂性能多个方面对重载交通环境下的桥梁结构特征进行综合性评价。经过研究后得出相关结论，具体作如下总结：

（1）在相同桥型时，桥梁跨径的增加将带来重车荷载响应水平的提高，但无论桥梁跨径如何变化，桥梁响应特征的变化趋势始终未受到其影响。

（2）连续箱梁桥的板（梁）的极值响应呈单峰特性，且通过与剪力极值响应特征的对比分析可知，正弯矩极值响应特征与之存在差别。

（3）车辆行驶规律对桥梁板（梁）的平均响应水平有明显的影响，3 号梁具有平均响应水平最高的特点。

（4）基于梁格法建立的有限元模型在分析重载交通作用下桥梁结构承载能力时具有可行性，在类似的桥梁结构承载性能分析工作中可引入此类方法，予以灵活应用。