高仿真拟人机械手弹性指关节结构设计研究

董艇舰，张 吉，王丹峰，吴孟丽

（中国民航大学航空工程学院，天津 300300）

1 引言

拟人机械手作为拟人机器人重要的组成部件之一，是机器人研究中不可或缺的部分。目前已有的拟人机械手大多通过铰链、连杆和万向节等机械结构刚性连接，虽然这类拟人机械手可以较好地模拟人手的运动，但本质上并没有脱离传统的机械连接，由于其自身结构上与复杂人手结构存在巨大差距，灵活性及运动特性远不及人手。区别于传统的机械手，高仿真拟人机械手从人手解剖学结构深入剖析人手运动的规律，更深入模拟人手关节的结构特征，达到高度仿真人手关节柔顺性和弹性的目的。

世界各国对于拟人机械手的研究从未停止，近年来，许多先进的拟人机械手已经得以开发研制并根据其各自在驱动速度、高自由度（DOF）等方面的独特功能在各个领域得以应用。文献［1］高度拟人化地模拟了人手的五指运动；文献［2］应用了协同运动理念，具有较强环境适应柔性；文献［3］是将生物学特征融合进机械手研究的成功典例。国内对于拟人机械手也日益蓬勃，文献［4］质量轻，具有较强适应性，适用于拟人机器人；文献［5］实现内置驱动使整个机械手微型化，达到了国际领先水平。尽管研究人员已经在控制和传感方面做出了大量努力来减小机械手与人手之间的差距，但从生物力学的角度来看，所做的工作是远远不够的。总结而言，限制拟人机械手发展的有两个关键约束条件，工程上缺乏准确的与人手相关的生物学知识以及传统的机械设计无法复制人手的生物力学特性。

因此，基于对拟人机械手的了解与认识，将人手的生物学特征与拟人机械手的研究相结合，剖析手指关节处的特殊形状及关节连接方式，提出一种高度仿真的同时具有与人手关节相似运动特性的弹性铰链指关节，以替代拟人机械手的刚性铰链关节，实现拟人机械手对人手的高度仿真。高仿真拟人机械手将对人类生活产生许多有利影响，可以更好地服务于诸如太空探索、灾情救援和假肢生产等领域。因此，基于生物解剖学特征开发一种高仿真拟人机械手弹性指关节是很有必要的，对今后拟人机械手的研究具有启示作用。

2 人手解剖学结构分析

人手作为上肢的主要组成部件，以灵活发展为主，人手的高度灵活度不仅依赖于大脑对其的控制，也与人手自身的结构息息相关。虽然人手的灵活度并没有一个准确的定义，但从生物学的角度看，骨骼长度、肌腱分布以及肌肉力量的差异都表明，灵活性是一个高度个人化的属性，其不仅取决于个人的运动控制能力，也与个体的独特生物力学特性息息相关。

就人手而言，手部19块骨骼（不包括8块腕骨）和14个关节的独特排列和活动性为发挥手部极度的功能适应性提供了结构性的基础［6］。从生物学角度分析可知，骨与骨间的关节连接有其独特的优势，而且这些结构凭借着高超的熟练程度相互配合。生物关节对骨骼的连接和灵活性有重要意义，因此对生物关节结构进行阐释。

从医学解剖学角度分析，人手骨关节主要由关节面、关节囊和关节腔构成。关节结构，如图1所示。骨关节中各骨之间的接触面定义为关节面，关节面上由光滑且富有弹性的关节软骨覆盖，使得其承重面大大增加，能够将骨骼承受的作用力均匀的分布在骨关节上。关节软骨同时能够减少骨关节运动过程中的撞击和震动。关节囊分为纤维层和滑膜层，纤维层主要由结缔组织构成。根据不同的骨关节和运动形式，纤维层的厚度也有所不同。厚度较大的纤维层称之为韧带，韧带能够起到连接骨关节和限制骨关节过度活动的作用。而较薄的结缔组织组成滑膜层，在周缘起到连接关节软骨的作用。关节软骨和滑膜层之间存在负压腔隙，其间含有一定的滑液，能够维持骨关节运动的稳定性。

图1 关节基本结构Fig.1 The Basic Structure of the Joint

就单关节结构而言，关节的稳定性需要由三方面维持，首先是关节面的构造形态，实现骨骼的协调和稳定，是关节稳定的基础；其次是两侧的韧带作用，维持了关节的静稳定；最后是肌腱控制，在运动过程中关节周围的肌腱实现了关节的动态稳定。为保证关节的稳定性，在设计关节结构时，应充分考虑这三方面的稳定作用。

显而易见，人手指关节连接与传统意义上刚性铰链的连接是存在差异的。传统上对于机械手的设计，将指关节作为刚性铰链，但事实上与人手自身的关节结构仍存在着差距。关节结构由于其本身的结构特点，使关节运动具有弹性，这是传统的铰链连接无法实现的。随着人们对机械手灵活性与仿真度的要求越来越高，为满足这种高仿真的需求，从人手关节入手，对机械手指关节进行高仿真结构设计。

3 指关节结构设计

如前所述，事实上骨与骨之间相邻关节面并不直接接触，由于韧带的伸缩作用，既保证了关节的运动同时骨与骨间不会脱节，且关节运动具有弹性，又搭配软骨与关节腔提高关节面抗冲击能力，保护关节面在受外力冲击的情况下不至于遭到强烈的破坏。

据此绘制简化的关节物理模型示意图，如图2所示（非结构比例，放大间隙以便观察）。构成关节的骨以线框表示，并突出关节头与关节窝结构，两者之间的软骨、关节囊和韧带结构以弹簧替代。当关节正常运动时，弹簧拉伸或压紧保证运动的可行性；当两侧受拉时，弹簧被拉伸，两侧关节面受到弹簧的拉力，使整个系统保持平衡并且骨与骨之间不会脱节，模拟了关节周围韧带的作用；当两侧受压时，弹簧被压缩，两侧关节面受到弹簧压力，使关节面与关节面之间不至于直接接触，模拟了关节腔的负压作用。故此模型可以模拟指关节处的基本功能结构。

图2 关节物理模型示意图Fig.2 Schematic Diagram of Physical Model of Joint

据上所示，为实现生物关节的弹性功能，从机器人学中获得启示。在机器人结构设计中，通过设计柔顺结构来实现机器人的柔顺性，作自适应调整，实现被动的柔顺［7］。被动式的柔顺控制总的来说是利用机器人内在的柔性实现。减轻两个刚体之间碰撞的一种常用措施就是加入缓冲。当刚体周围有弹性元件连接时，就对外力有了柔顺性。用软性材料制成的机械手在人机交互中具有更好的安全性与真实感。

结合人手生物学结构以及机器人学的相关知识，依据真实人手骨骼的三维扫描数据文件，对不同骨骼特征结构进行分析，设计合理的模型结构，实现弹性铰链关节。

3.1 指间关节

就指间关节的关节面而言，其双髁结构有着独特的优势特点，既防止关节面在运动过程中不必要的左右滑动，也保持了伸屈运动的稳定性。故而，结构化的指间关节保留并强化了这一特点，在关节窝处延伸出连接结构插入关节头的连接结构中。

由于指间关节处关节运动圆心变化较小，对于指间关节处由韧带结构构成的关节弹性，用刚性轴加弹性轴套构成相似的弹性效果，使关节结构较之刚性铰链更加接近人手关节特性。指间关节的三维模型结构，如图3所示。在刚性轴与关节头相连部分安上弹性轴套，实现机器人的柔顺控制。

图3 指间关节三维模型结构Fig.3 3D Model Structure of Interphalangeal Joint

结构设计中考虑真实人手关节的活动范围，控制连接结构可到达的极限位置，结合弹性结构，使其到达极限位置之后仍有一定的弹性位移量，模拟人手的关节弹性结构。对于指间关节所设计的弹性铰链关节，由于其自身结构的特殊性，满足了生物学上人手关节的被动关节活动度，而对于传统铰链来说，只存在主动关节活动度，因此弹性铰链关节可以高仿真人手关节，实现运动关节的运动特性。

3.2 掌指关节

在掌指关节处，由于关节运动圆心随位置变化较大，刚性轴加弹性轴套的结构不适用于此。一般在设计掌指关节时，习惯将掌骨头设计成一个球体，但掌骨头有其自身的特点。掌骨在掌侧与外侧的掌骨头部顶部圆弧是有差异的，并不是一个标准圆球，掌侧的头部弧度相对较大，而外侧的弧度则相对较小，因此也从骨外形上解释了掌指关节处侧摆幅度相对于屈伸运动而言较小。非标准圆球的掌骨头的凸轮形状增加了掌指关节弯曲时侧副韧带近端和远端附着点之间的距离（伸时距离为27mm，90°屈时距离为34mm）［8］。这与指间关节相反，指间关节的侧副韧带的近端与远端附着点的距离在弯曲过程中基本保持稳定。掌指关节处侧副韧带结构除了增加关节稳定性，还可以对掌指关节的活动范围起到一定控制作用。

分析人手解剖学结构，将掌指关节设计为一个椭球结构。掌侧侧摆弧度较小，为大圆弧，外侧屈伸范围较大，为小圆弧。基于侧副韧带的稳定作用，由弹性绳模拟生物韧带结构，依据韧带的基本分布，稳定关节，高度仿真人手关节结构。对于这类关节，韧带连接位置至关重要，分析解剖学结构中关节两侧侧副韧带以及掌板的分布结构，故该处具体模型，如图4所示。

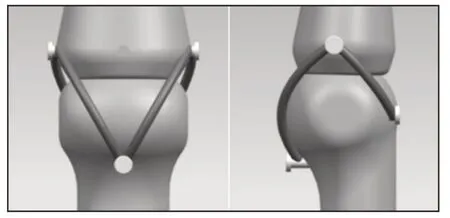
图4 掌指关节三维模型图Fig.4 3D Model Diagram of Metacarpophalangeal Joint

3.3 单指样品模型

对单指进行指节的3D打印以及结构安装，如图5所示。样品模型满足运动需求，且在指关节处具有一定的弹性，高度仿真了人手指关节的弹性运动特征，验证了结构设计的合理性。

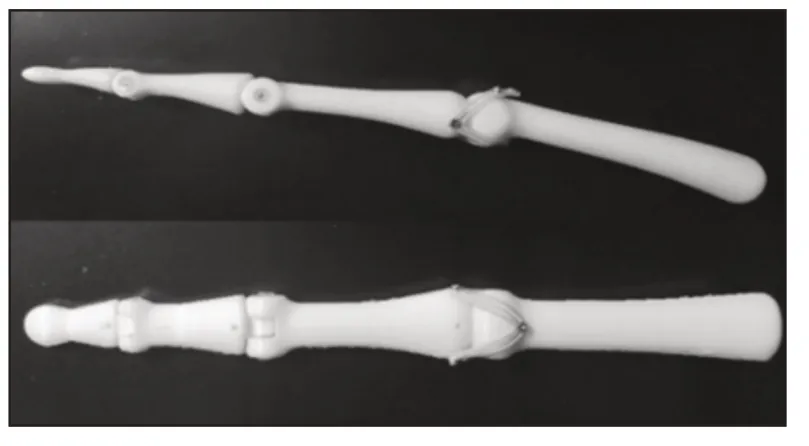
图5 3D打印并安装的单指样品模型Fig.5 3D Printed and Installed Single Finger Sample Model

4 运动学分析

机械手运动学研究的主要内容是手指末端的位姿、速度和加速度与手指各关节的位姿、速度和加速度之间的关系［9］。对手指的正向运动学和逆向运动学分析，求解出手指各关节位姿和指尖在基坐标位姿的关系。人手的五指结构基本相似，分析其一即可。因此这里选择拟人机械手中指进行运动学分析。

4.1 单指坐标系建立

建立单指的坐标系，如图6所示。X0Y0Z0为定参考坐标系，其他为动坐标系。指尖上的点P坐标为（x，y，z），手指各指节的长度分别为a1，a2，a3，a4，各关节转角分别为θ1，θ2，θ3，θ4，各关节扭角分别为α1，α2，α3，α4，各关节之间的距离分别为d1，d2，d3，d4。

图6 手指坐标系Fig.6 Finger Coordinate System

4.2 手指正向运动学分析

以中指为例，手指的运动学模型主要由以下四个参数描述。手指D-H参数表，如表1所示。

表1 中指的D-H连杆参数表Tab.1 The D-H Connecting Rod Parameters of the Middle Finger

相邻指节坐标系转换矩阵为：

将表1 中各参数带入到式（1）可以得到对应的A1、A2、A3、A4变换矩阵。

拟人机械手手指末端上的P点相对于坐标系X0Y0Z0的变换矩阵为：

其中：

由式（2）可得指尖P点位置为：

4.3 手指逆向运动学分析

在已知手指之间在坐标系中的位置和姿态时，即已知指尖P点位置，故可推知：

因远端指骨和中节指骨通过腱绳传动，存在协同运动，协同运动的传动比为K，由此可得：

将式（5）和式（7）的等号两边平方后分别相加，整理得：

求解式（9）可以求得cosθ3，进而求得θ3。由式（5）经三角函数转换得：

令A=a4s34+a3s3，B=a4c34+a3c3+a2，C=z

则式（10）可以写成：Ac2+Bs2=C。

利用三角代换得：

式（6）、式（9）、式（11）是单指的逆运动学方程。如果指尖在基坐标系中的位置（x，y，z）在手指的工作空间内，则可以求出关节角θ1，θ2，θ3，θ4。

4.4 运动学仿真验证及工作空间分析

利用MATLAB中的Robotics Toolboxs工具箱，绘制出中指的连杆坐标系模型，如图7所示。其中各圆柱的中心是连杆坐标系的原点，图7所示的连杆模型与图6中建立的手指坐标系一致，也验证了D-H参数表的正确性。通过调用teach 函数，可以通过控制机械手各关节角度的变化，清晰地观察机械手的不同位置姿态。机械手在到达目标工作位置的过程中，各个关节需同时运动才能到达最终的目标位置。通过模型对其进行模拟，模拟结果位置参数与所求解相同，即计算得到的运动学正解是正确的。

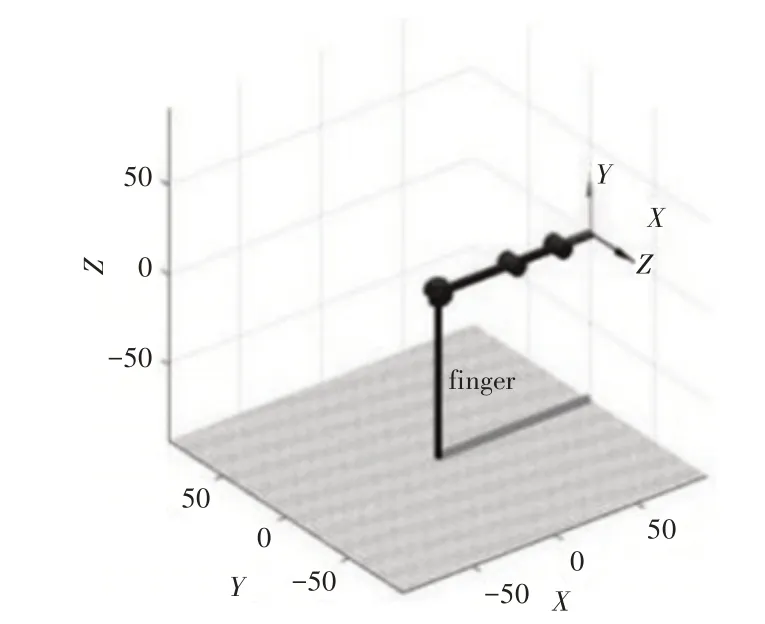
图7 中指MATLAB连杆模型Fig.7 MATLAB Connecting Rod Model of the Middle Finger

对其套用逆解公式求解。将其各个位置参数带入逆运动学方程，可求得其逆解。通过模型对其解进行验证，将各个角度带入，可知其解与机械手位置数据基本吻合，故所求运动学逆解的正确性得以验证。

求取指尖工作空间是测验机械手是否满足手指运动空间需求以及评价其工作性能的重要指标之一。单指工作空间受关节活动范围以及连杆长度影响，由机构中各运动副相互配合后运动副自身所能达到的最大工作范围相互制约形成。这里为求解单指指尖的工作空间，采用数值法中的蒙特卡洛法（Monte Carlo method）。蒙特卡洛法是利用数学中概率的思想以概率统计为理论指导的方法，通过随机采样（或通过模拟随机变量）解决数学问题的数值方法［10］。

这里研究的拟人机械手指各骨节长度依据真人指骨长度确定，其中，远端指骨长为20mm，中节指骨长为28mm，近端指骨长为45mm，各关节活动范围由人手关节活动范围确定，其中，远端指间关节屈伸范围为（-10～70）°，近端指间关节屈伸范围为（0～110）°，掌指关节屈伸范围为（0～90）°，侧摆范围为（-20～20）°。设置10000个原始随机点，在MATLAB中得到机械手指尖工作空间的分布情况，如图8所示。

图8 中指工作空间点云图Fig.8 The Workspace Point Cloud Map of the Middle Finger

如图8（b）所示，x-y平面的工作空间呈现出一个交叉点，考虑生物学上掌指关节运动到极限位置时，两侧侧副韧带处于张紧状态，此时关节不再可以做侧向摆动，符合工作空间点云图情况。如图8（c）所示，在x-z平面上可以更清晰显示各关节极限位置给工作空间带来的影响，就最远端的外弧而言，大致可以分为三个圆弧，首先是第一象限中，以原点为中心，三根连杆为直径的大圆弧，其次是第二三象限中，以掌指关节90°极限值时近端指骨的远端为中心，远端及中节指骨为直径的中圆弧，最后是第三象限中，掌指关节与近端指关节到达极限位置后，远端指骨的轨迹圆弧。如图8（d）所示，可以比较鲜明地看出掌指关节的侧向活动范围对工作空间的影响，其大大增加了指尖的工作空间范围。仿真结果与实际工作空间相吻合。

5 结论

基于人手指关节解剖学结构，建立生物关节物理模型，结合机器人学相关知识，设计了一种具有与人手运动特性相似的弹性铰链关节，在保证灵活运动的基础上，也实现了指关节的弹性特征，满足高仿真的需求。

为实现运动控制，对手指进行正、逆运动学求解，然后在MATLAB中进行运动学仿真验证，并应用蒙特卡洛法进行指尖工作空间求解，得到的工作空间满足手指工作空间需求，符合人手运动规律。

在后续工作中，拟将该指关节结构应用于高仿真拟人机械手，并基于生物学手部肌腱分布规律辅以腱绳控制，实现对高仿真拟人机械手的运动控制。