轴类零件素线直线度误差评定方法的研究

韩宗旺，张 伟，程 祥，郑宏宇

（山东理工大学机械工程学院，山东 淄博 255000）

1 引言

根据国家标准规定，直线度误差定义为被测实际直线相对于理想直线的变动量，并且根据不同的要求，直线度公差带的形状可以分为给定平面内的直线度误差、给定方向上的直线度误差、任意方上的直线度误差［1］。这里所测量的轴线轮廓直线度属于给定平面内的直线度误差。平面内直线度误差评定方法有：最小包容区域法、最小二乘法、两端点连线法等［2］。其中后两种方法得到近似值，最小包容区域法评定精度最高，但《GB/T 11336-2004直线度误差检测》［3］中没有清晰地给出最小包容区域法的实现方法。

基于机器视觉检测零件直线度，多采用最小二乘法与两端点法［4-6］，当零件变形较大时，线性关系降低，两种方法就不适用。为快速、精确的对轴类零件直线度误差进行评定，利用机器视觉检测平台采集了多张轴零件的图片，以提取的轴的素线坐标为依据，分别用两端点法，最小二乘法，以及所提出的约束旋转逼近法、包容线搜索算法和多变异位自适应遗传算法进行直线度评定，比较各评定方法精度和优缺点。为了进一步验证三种方法的准确性，利用该三种方法对其它文献中的数据进行评定，并与文献中的结果进行比较。

2 直线度评定方法

2.1 两端点法

两端点法是将首尾两个端点连接成一条直线，然后此连线作为评定基准直线，找出采样点与直线距离的最大值hmax和最小值hmin，建立直角坐标系xoy，则直线度误差为d1=hmax-hmin，如图1所示。

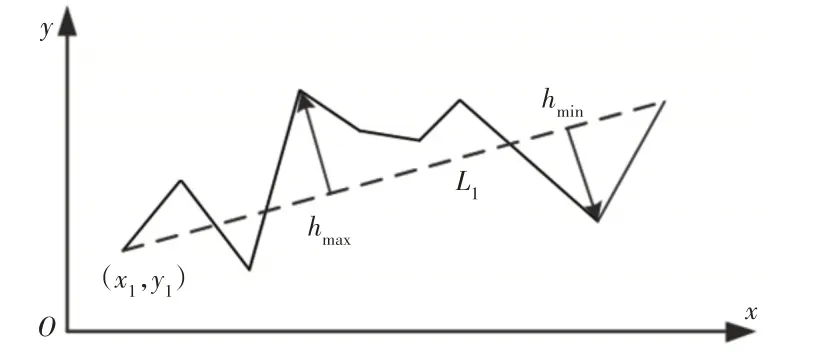
图1 两端点法原理图Fig.1 Schematic Diagram of Two-Point Method

2.2 最小二乘法

最小二乘法［7］是将采样点先进行最小二乘拟合出直线作为评定基准直线，找出采样点与基准直线L2距离的最大值hmax和最小值hmin，则直线度误差为：d2=hmax-hmin。其原理图，如图2所示。

图2 最小二乘法原理图Fig.2 Schematic Diagram of Least Square Method

2.3 约束旋转逼近法

约束旋转逼近法是通过算法对搜索范围进行约束，其原理与实现方法如下：

首先将采样点进行最小二乘拟合，得到基点P，计算全部采样点到最小二乘直线的距离，假设得到最大值点M1与最小值点M2位置，如图3所示。将这两个点分别与P点相连，两直线夹角β即为搜索范围，如式（1）所示。

图3 约束旋转逼近法原理图Fig.3 Schematic Diagram of Constrained Rotation Approximation Method

由搜索次数得到斜率变化量μ，如式（2）所示。

式中：e—搜索次数。进而得到分割基线方程为：

初始最小二乘直线绕P点在搜索范围内逆时针和顺时针分别旋转角度，计算每一条分割直线对应于所设角度的直线度误差值，假设L4位置的时候直线度误差值最小，计算采样点到该直线距离的最大值hmax和最小值hmin，则直线度误差d3=hmax-hmin。

2.4 多变异位自适应遗传算法

最小区域法［8-9］实际上是寻找包容被测轮廓的两平行直线之间距离的最小值。包容被测轮廓的两平行直线存在无数对，但只有一对距离最小。换言之，一对理想包容参考直线其斜率值可以有无数个，但要符合最小条件使两平行包容线之间距离最小，只有一个斜率是最佳的。因此，可以用多变异位自适应遗传算法来解决这个最优化问题［10］。

本方法在最小包容区域法思想上，结合自适应改变交叉概率与变异概率以及多变异位方式的遗传算法的优点，寻找两条最小包容平行直线的最佳斜率k，求斜率为k的包络所有点的两条直线截距，进一步计算出直线度误差，具体过程如下：

（1）根据被测点坐标，用最小二乘法拟合出参考直线，得到直线斜率k。

（2）确定种群规模N、交叉概率Pc1、Pc2，变异概率Pm1、Pm2和最大进化代数M。

（3）编码构成初始种群A0（t）。由于最优解与最小二乘解的斜率偏差很小，所以选择解搜索区间为（k-1～k+1）并对斜率进行二进制编码构成初始种群。

（4）计算个体适应度fi。目标函数为N个个体所对应的直线度误差：

式中：D—直线度误差，即两条最小包容平行直线之间的距离；dmax、dmin—两条最小包容平行直线所对应的截距；k—平行包容直线斜率。

由于目标函数的变化方向和适应度相反，将目标函数取倒数作为适应度函数，其映射关系为：

（5）选择操作，采用轮盘赌选择法，经过选择后得到N个新个体A1（t）。

（6）交叉操作。首先引入交叉概率和变异概率调整函数，使得交叉概率和变异概率随着个体适应度的大小和群体的分布程度自动调整［11］：

式中：fmax、favg—计算群体中最大适应度值和平均适应度值；f'—待交叉的两个体中适应度较大的一个；f—待变异个体的适应度值。

从新个体中以相同概率独立的选择两个个体，产生一个［0，1］的随机数，如果该随机数小于交叉概率，则个体1和个体2进行交叉操作，产生两个新个体；否则保留原个体，不进行交叉操作，重复此过程，直到形成过渡种群A2（t）。其交叉示意图，如图4所示。

图4 二进制编码交叉操作Fig.4 Binary Code Crossover Operation

（7）变异操作。计算种群中适应度的最大值与最小值是否相等，如果相等，根据变异概率，随机产生过渡种群中个体的一个变异位；如果不相等，则计算最大适应度值与个体适应度值之差，最大适应度值与最小适应度值之差，若两者比值大于MM，则随机产生过渡种群中个体的三个变异位，若比值大于1小于MM，则随机产生过渡种群中个体的两个变异位。这样便形成新一代的种群A3（t），然后计算新一代适应度值。

（8）检查进化代数是否达到预设值。

（9）保存适应度最大的个体其所对应的目标函数值即为最终的直线度误差值。

2.5 包容线搜索算法

针对已有符合最小包容区域法定义方法在计算直线度误差迭代速度慢、计算复杂的缺点，提出根据最小包容区域原则的包容线搜索算法来评定直线度误差方法。

首先利用最小二乘法得出拟合基线L3，如图5所示。设其直线方程为：

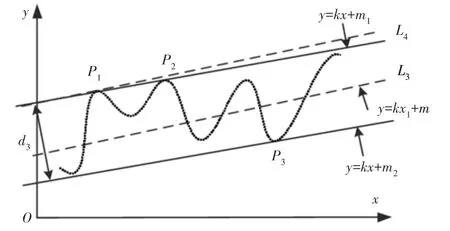
图5 包容线搜索算法原理图Fig.5 Schematic Diagram of Envelope Search Method

以基线为界将采样点分为高点和低点，寻找离拟合线距离最远高点P1，以P1点为基点，以最小二乘拟合直线斜率k1做一条直线L4，通过改变直线L4的斜率使采样点均位于直线下方或直线上，确定临界点P2。

若最小二乘拟合直线斜率大于0，则直线L4应顺时针转动，a取负值；如果斜率小于0，则直线L4应逆时针转动，a取正值，然后根据斜率ki变化计算出相应的截距，其公式为：

将除P1外的其它测点坐标带入式（11）中，ki每变化一次，对采样点进行计算，理论上当W=0时得到临界点P2，但实际上由于步长a大小的设置，会出现临界点P2处于两次扫描直线之间的情况，此时需满足：

根据P1、P2点确定相对应的上包容线y=kx+m1，然后过最远采样点P3作与直线平行的下包容线y=kx+m2，此时P1、P2、P3，三个点满足最小区域的“高低高”准则。计算两包容线之间的距离即为直线度误差。

以同样的方法先找下包容线，寻找满足最小区域的“低高低”准则的三点，然后按上述步骤计算后也会求得一对包容线的距离，将两次计算得到的距离最小值作为所求直线度误差。

3 直线度误差评定实验

3.1 轴的素线直线度检测

为比较各种直线度误差评定算法的精度，利用基于机器视觉的轴类零件直线度误差测量的平台，采用CMOS 相机（型号：MER-2000-19U3C）作为检测相机，测量100×φ20mm 轴的素线直线度误差，采集了若干张轴的图像，如图6所示。经图像滤波、阈值分割、形态学操作等，提取轴的边缘图像，如图7所示。

图6 机器视觉采集被测轴图像Fig.6 Machine Vision Acquisition of the Measured Axis Image

图7 轴的上下边缘检测图Fig.7 Upper and Lower Edge Detection Graph of Shaft

对CMOS相机进行标定，提取图像素线轮廓坐标数据，共有2776个像素数据。为了便于计算和数据显示，将图像坐标原点进行平移，采用两端点评定方法得到的直线度，如图8所示。采用最小二乘法评定方法得到直线度误差，如图9所示。

图8 两端点法直线度评定Fig.8 Straightness Evaluation by Two end Point Method

图9 最小二乘法直线度评定Fig.9 Straightness Evaluation by Least Square Method

采用约束旋转逼近法时，根据搜索区域确定β角度约为1°，顺时针逆时针旋转角度各为0.5°，根据式（1）～式（3），选择搜索次数e=400次，则μ=4.36×10-5。结果，如图10所示。采用包容线搜索算法时，a为一个数值很小的步长，a太小会影响计算速度，太大则会影响计算结果，这里a取值为10-5，结果，如图11所示。

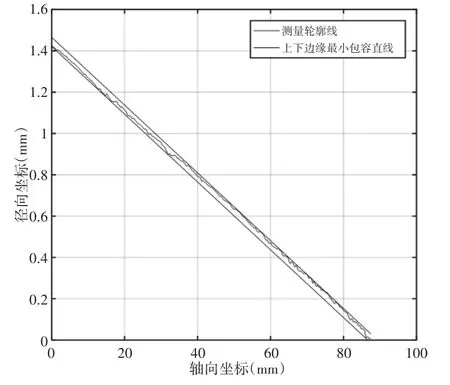
图11 包容线搜索直线度评定Fig.11 Straightness Evaluation of Envelope Search

采用多变异位自适应遗传算法时，选取种群规模为N=300，交叉概率Pc1=0.6、Pc2=0.9，变异概率Pm1=0.01、Pm2=0.04，最大进化代数M=300，结果，如图12所示。

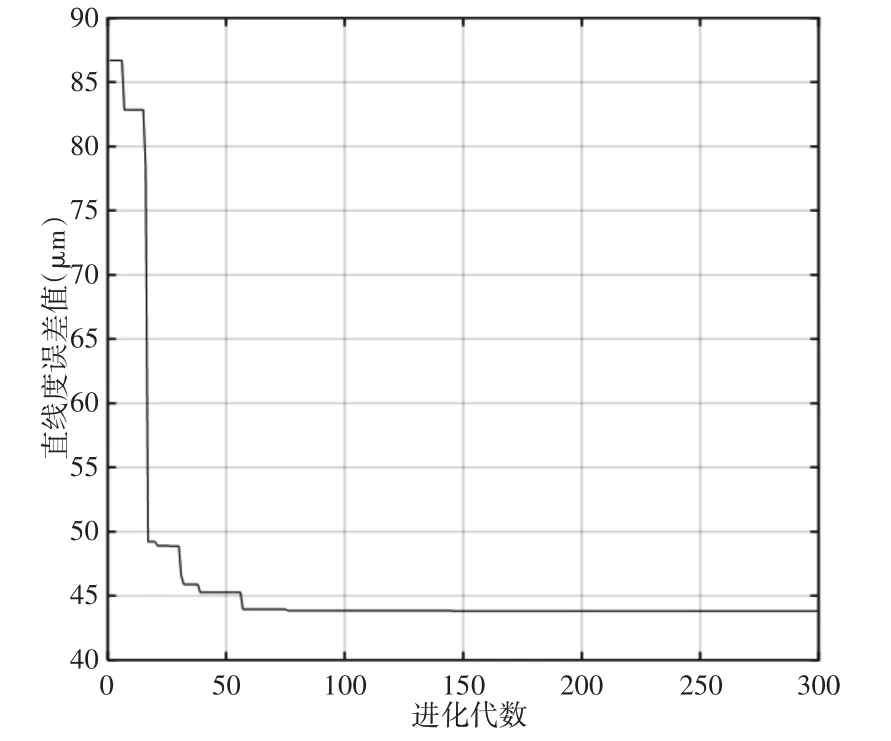
图12 多变异位自适应遗传算法的直线度评定Fig.12 Straightness Svaluation of Multivariate Heterotopic Adaptive Genetic Algorithm

4 结果分析

经过多次重复实验，其运算结果表明，两端点法和最小二乘法评定结果与其它方法评定结果相差较大；采用包容线搜索算法、约束旋转逼近法和多变异位自适应遗传算法评定结果相差较小，较前两种方法精度均有提高，其中多变异位自适应遗传算法的评定精度最高，但运行时间最长，而包容线搜索算法、约束旋转逼近法运行时间比较短。各算法直线度评定结果，如表1所示。

表1 各算法评定结果Tab.1 Calculation Results of Each Algorithm

5 结果比较

文献［12］中分别用传统遗传算法、粒子群算法对16个数据采样点数据进行直线度评定，数据，如表2所示。为验证这里算法的准确性，利用文献数据对这里的三种评定方法进行验证，并绘制出评定数据处理后的曲线图，如图13～图15所示。

表2 文献［12］评定数据Tab.2 Evaluation Data of Literature［12］

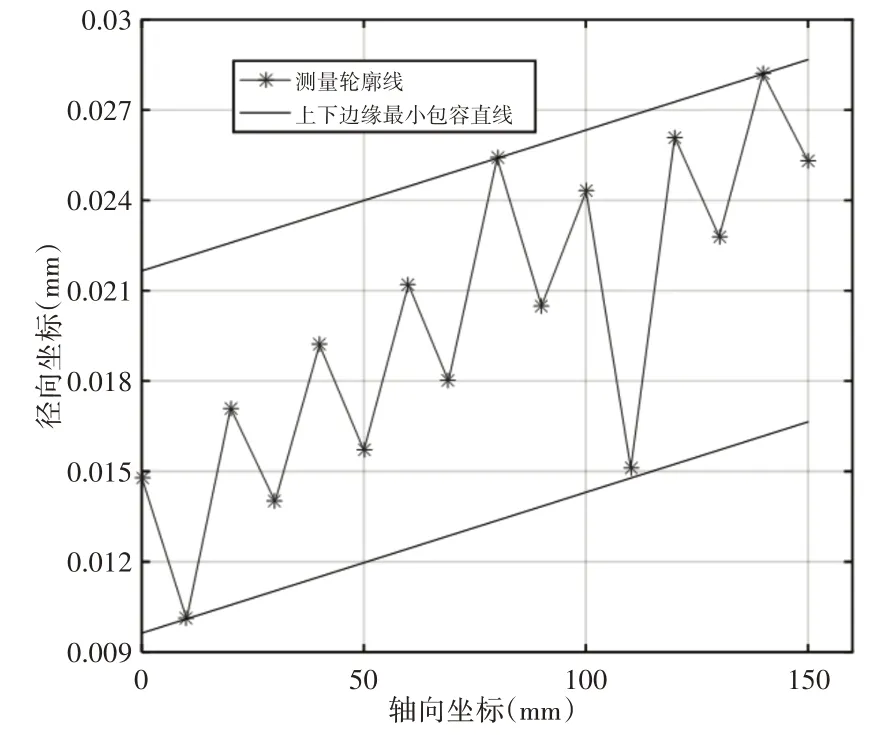
图13 包容线搜索算法评定Fig.13 Evaluation of Envelope Search Algorithm

图14 约束旋转逼近法直线度评定Fig.14 Straightness Evaluation of Constrained Rotation Approximation Method

图15 多变异位自适应遗传算法的直线度评定Fig.15 Straightness Evaluation of Multivariate Heterotopic Adaptive Genetic Algorithm

表2数据采用文献［12］中的评定方法评定结果，如表3所示。采用包容线搜索算法、约束旋转逼近法和多变异位自适应遗传算法评定结果，如表4所示。

表3 文献［12］中的评定结果Tab.3 Evaluation Results in Literature［12］

表4 数据评定结果Tab.4 Data Evaluation Results

通过比较表3、表4的结果得到：利用提出的包容线搜索算法和约束旋转逼近法得到的直线度误差与文献［12］中的传统遗传算法、粒子群法得到的直线度误差基本相同，多变异位自适应遗传算法的检测结果（0.011804）比文献［12］中遗传算法（0.011958）结果误差更小；且与文献［12］中粒子群算法结果基本一致，但这里的方法收敛速度更快。

6 结论

机器视觉检测轴类零件素线直线度常用最小二乘法与两端点法进行评定，为进一步提高检测精度，提出约束旋转逼近法、多变异位自适应遗传算法和包容线搜索算法三种直线度评定方法，对视觉检测所提取的轴素线坐标直线度误差进行了评定。结果表明：约束旋转逼近法、包容线搜索算法和多变异位自适应遗传算法的评定精度高于两端点法和最小二乘法。约束旋转逼近法和包容线搜索算法运行时间基本相同，多变异位自适应遗传算法运行时间最长。最后采用此三种方法对文献数据评定与结果比较，结果表明这三种方法和文献的评定结果基本一致。因此，约束旋转逼近法、多变异位自适应遗传算法以及包容线搜索算法都能够很好满足精确的检测与评定需求，在视觉检测零件直线度中可以根据检测时间和精度进行选择。