基于CKAM-Resnet的滚动轴承故障诊断

周 勃，曾劲松，刘国宁，马光岩

（郑州大学机械与动力工程学院，河南 郑州 450001）

1 引言

滚动轴承是旋转机械中广泛使用的关键零件之一，由于复杂的工作环境和多变的工况极易产生故障，带来严重的安全隐患［1］。根据不完全统计，大约有三分之一的旋转机械故障是由轴承故障引起的，因此对轴承故障信息检测和诊断对保障机械设备正常运行具有重要意义。

常见的轴承故障智能诊断方法常采用人工的选取轴承振动信号特征然后再利用传统机器学习方法对故障类型进行模式识别和分类，但是往往需要对振动信号做复杂的信号处理以获取相对满意的特征，难以达到较好的分类精度。近年来，有诸多学者尝试将深度学习技术引入故障诊断领域。深度学习作为机器学习的重要分支之一［2］，在复杂特征提取方面具有传统机器学习方法不可比拟的优势，更能充分利用数据，可以自动学习到数据中的深层隐藏表示，从而避免了繁琐的特征工程。史光宇将轴承振动的一维振动信号顺序采样并重构成二维灰度图作为卷积神经网络（CNN）的输入，有监督的对轴承进行智能故障诊断［3］。文献［4］构建了一种残差学习的深度一维卷积自编码器，可以无监督的对齿轮箱故障进行诊断。文献［5］通过堆叠LSTM可以自动分层提取原始时间信号中固有的特征，对滚动轴承诊断并取得了不错效果。文献［6］则将CNN模型改进，提出了SECNN模型，通过自适应调整模型提取的特征通道维权重，提升了故障诊断的准确率。以上方法表明深度学习方法在轴承故障诊断方向具有很强的可行性，但是均未考虑到深度模型在训练过程中可能存在的梯度弥散现象，且在故障特征的提取能力方面仍有很大的提升空间，为了进一步提升故障诊断模型的综合性能，提出了一种基于CKAM-Resnet的轴承故障诊断模型，大大增强了对故障特征的提取能力，同时使模型更容易训练。

2 残差网络

残差网络（Residual Networks，Resnet）由何凯明提出，通过在网络中加入短路连接（Shortcut Connection），有效解地决了深层神经网络模型的退化问题［7］。残差网络的基本结构是由若干个残差块堆叠而成，如图1所示。基本思想是模型的内部结构至少要保有恒等映射的能力。残差网络直接把恒等映射作为网络的一部分，将网络设计为H(x) =F(x) +x，把问题转变为去求解一个残差映射函数F(x) =H(x) -x，若使得F(x) = 0就构成了一个恒等映射，如果新添加的层可以被训练成恒等映射H(x) =x，则加深后的新网络至少不会导致性能下降，拟合残差比拟合恒等映射更为简单，且残差映射更容易被优化。

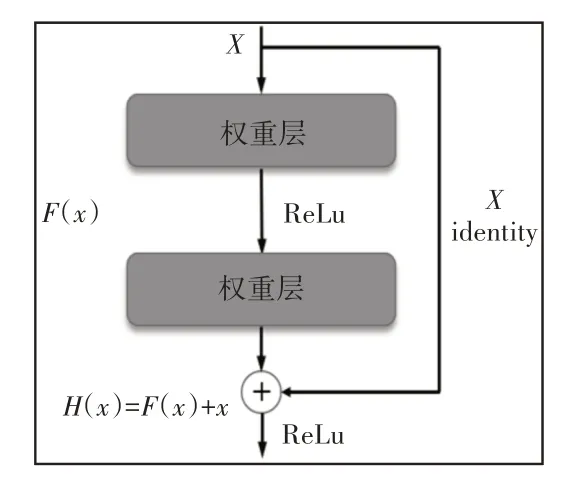
图1 残差块结构Fig.1 Residual Block Structure

假设残差神经网络有L个残差块堆叠而成，用x(l)表示第l个残差块的输入，x(l+1)表示该残差块的输出。则第l个残差块的输出可以推导出为：

递归可以得到第L个残差块的输出：

其中{}代表第l个残差块中所有层的权值矩阵，假定第L个残差块的误差为L，对于网络第l个残差块根据链式求导法则由（2）计算梯度为：

由式（3）可以观察到，第一个偏导项不涉及任何权值层，能保证信息直接传递到任意一个比它浅的l层，而括号中第二个偏导项在训练过程中不会始终保持为-1，意味着梯度不可能一直为0，反向传播过程中链式求导从连乘变成连加，可以有效的避免梯度消失和梯度弥散现象。

3 卷积核注意力机制（CKAM）

在神经科学领域，动物的视觉皮层的神经元的感受野的大小可以根据外界刺激的不同自适应的改变，实验发现神经元的大小并不是固定的而是受刺激调节的［8］。选择性核卷积（Selective Kernel Convolution，SK卷积）的运作方式与之类似，将注意力机制应用于不同尺度的卷积核中，采用门控思想来控制信息的流动以达到神经元接受刺激而自适应的改变感受野的目的，实现了卷积核的注意力机制（Convolution Kernel Attention Mechanism，CKAM）。其核心思想就是用多尺度特征汇总的信息来跨通道的地指导如何分配侧重使用哪个卷积核的表征。

以二维选择性核卷积为例，其结构，如图2所示。选择性核卷积由分裂（split），融合（fuse）和选择（select）三种运算组成，X代表输入的任意特征图。首先进行分裂（split）运算，在2个分支的情况下，（多分支与之类似），分别使用大小为（3×3）和（5×5）的卷积核对输入的特征图X进行卷积，得到分裂后大小相同且含有不同尺度信息的特征图͂和̂。融合（Fuse）运算通过元素求和汇集了多分支的信息，其中U是融合后的特征图，即：

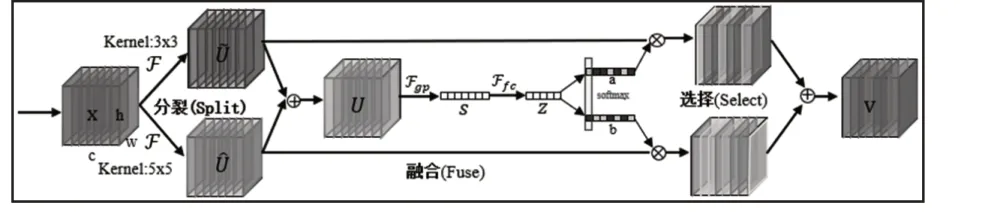
图2 选择性核卷积操作Fig.2 Selective Kernel Convolution Operation

式（5）显示了全局均值池化的操作，Sc代表第c个通道经过该操作后的结果。U经过全局均值池化后得到含有融合多分支空间信息后的特征s（s∈RC×1），特征s经过全连接被压缩成低维紧凑特征z（z∈Rd×1）来指导特征的自适应选取，其中δ表示：

ReLU激活函数，B表示批量归一化操作，W表示全连接层的权值矩阵，其中W∈Rd×c。选择（select）运算则是对紧凑特征z通过两个分支的软注意力（Soft Attention）矩阵［9］A和B(A，B∈RC×d)）进行仿射变换，并对A，B对应的通道维度进行softmax操作，最终可以得到含有2 个分支不同尺度卷积核的通道权重：wA，wB（wA=[a1，a2，…，ac]，wB=[b1，b2，…，bc]），其中Ac和Bc分别是软注意力矩阵A，B中第c个通道的软注意力向量，ac和bc分别为经过softmax后两个分支第c个通道上的权重大小。

接着将wA，wB分别与输入特征图X分裂出的特征图͂和̂进行元素相乘得到不同卷积核大小的2个分支通道权重调整后的特征图，并把2 个特征图再一次融合得到最终的特征V。（V=[V1，V2，…，Vc]，V∈RH×W），其中由式（8）可以得到最终特征图在通道c上的特征）。

最终经选择性核卷积得到特征图V与普通卷积操作得到的特征图相比汇集了更为丰富的不同感受野的空间融合信息。

4 基于CKAM-Resnet故障诊断模型

针对滚动轴承振动信号的特点，将选择性核卷积可以获取更为丰富的不同感受野的空间融合特征的特点与残差网络可以避免解决梯度消失/弥散且容易训练的优势相结合构建出了一种基于CKAM-Resnet的滚动轴承故障诊断模型。

CKAM-Resnet 的模型结构借鉴了残差网络的思想，将选择性核卷积设计成了块的结构，模型由堆叠的一维选择性核卷积块（1D-SKBlock，SK块）构成，如图3所示。模型的具体结构，如图4所示。为了提取轴承振动信号的短时特征，第一层卷积层采用步长为15，宽为128 的一维宽卷积核，后接（1×2）的一维最大池化层，将输入的特征图缩小的同时加大了深度，模型各层激活函数均采用线性整流函数（Relu），并且每一个卷积和池化层后均引入BN 层（Batch Normalization）［10］加快模型训练过程的收敛减轻过拟合。经池化后的特征图接着通过3个SK块，其中每经过一个SK 块都会将输入的特征图通道数加倍的同时使特征图大小减半，为减小模型参数量提升计算速度，每个SK卷积层的分裂运算均采用2分支的一维卷积，卷积核大小分别是（1×3）和（1×7）。SK块后采用一维全局池化层对空间信息进行了求和，使模型对输入的空间变换更具有稳定性，并进一步减少了模型参数量，最后经过线性层，引入dropout机制防止模型出现过拟合，将输出特征降维到10，并经过Softmax层输出预测概率值。模型的具体结构参数设置，如表1所示。

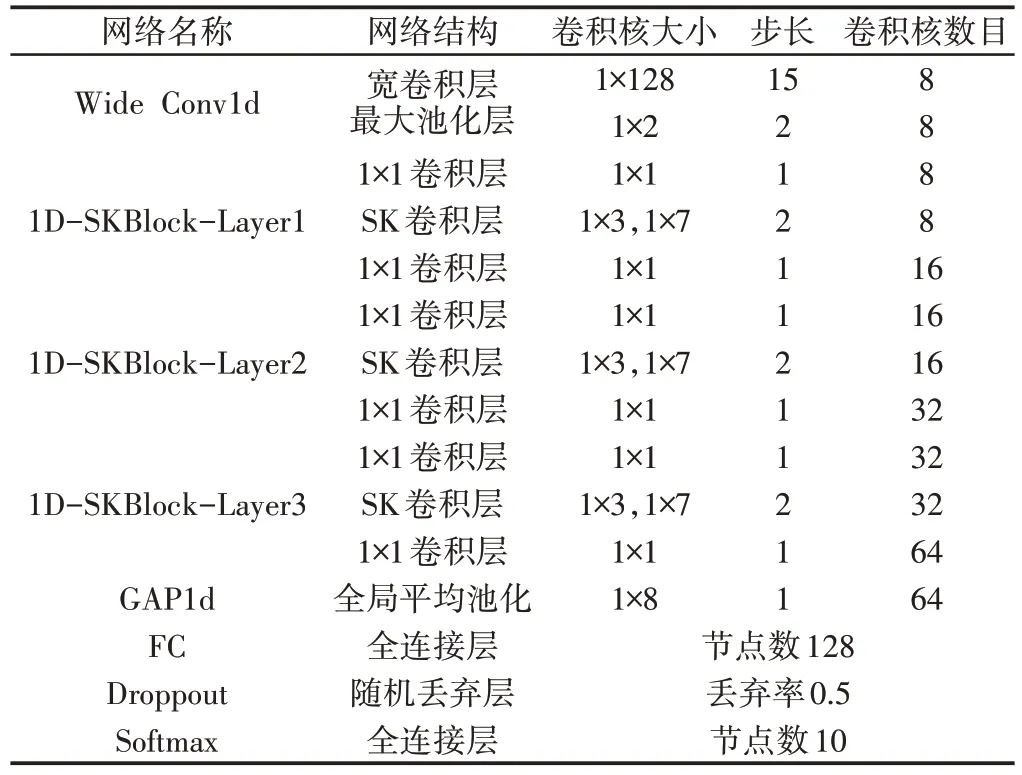
表1 网络模型具体参数Tab.1 Network Model Specific Parameters

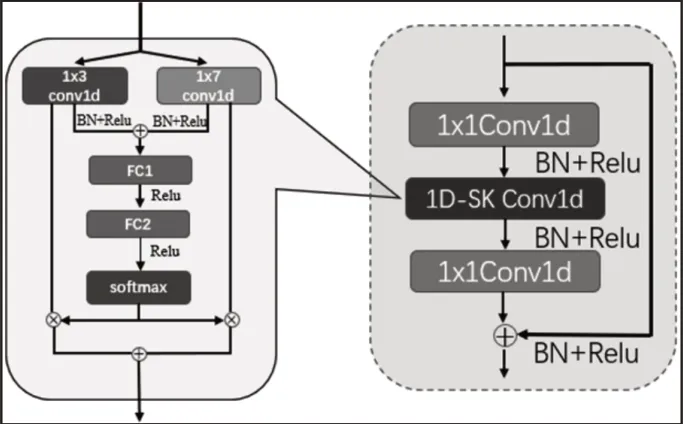
图3 一维选择性核卷积块（1D-SKBlock）Fig.3 1D Selective Kernel Convolution Block

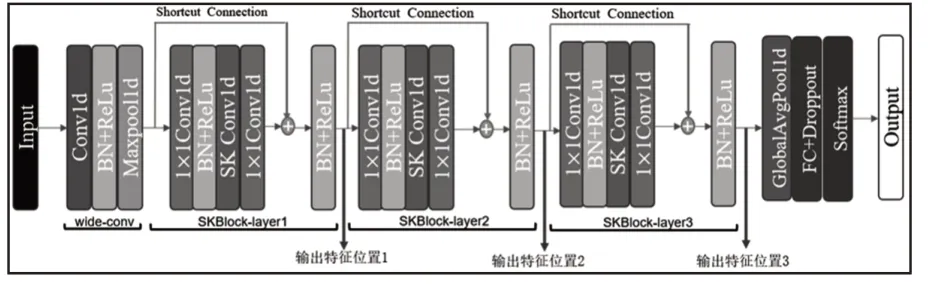
图4 CKAM-Resnet故障诊断模型结构Fig.4 CKAM-Resnet Fault Diagnosis Model Structure

5 实验过程及结果分析

实验采用的滚动轴承振动数据来自美国凯斯西储大学（Case Western Reserve University，CWRU）轴承数据中心经轴承数据采集系统测试得到的公开数据集［11］。该轴承数据采集系统由电机，转矩传感器，功率计及电子控制设备组成，轴承引入的故障均为由电火花加工而成的单一故障，损伤直径分别为0.007in，0.014in，0.021in（1in=25.4mm），分别位于轴承内圈、滚珠和外圈部位。

为验证提出的故障诊断模型对滚动轴承的故障诊断的实际效果，实验采用采样频率为12kHz，电机负载分别为1、2，3hp条件下（1hp≈0.735kW），电机转速分别为1772r/min，1750r/min，1730r/min，型号为SKF6205-2RS的驱动端轴承的振动数据。按轴承损伤位置和直径的不同，将轴承振动数据划分为包括正常状态在内的10种状态标签，并将2048个采样点数划分为一个样本，根据不同负载情况，将数据集分划为训练集、验证集和测试集。为了防止训练集的样本过少导致模型过拟合，对数据集利用重叠采样的数据增强技术进行了扩充［12］，并采用z-score标准化对输入的样本数据进行了预处理。最终每种负载情况下每种故障类型均有400个样本作为训练集，50个样本作为验证集，50个样本作为测试集。单种负载下具体实验数据集详情，如表2所示。

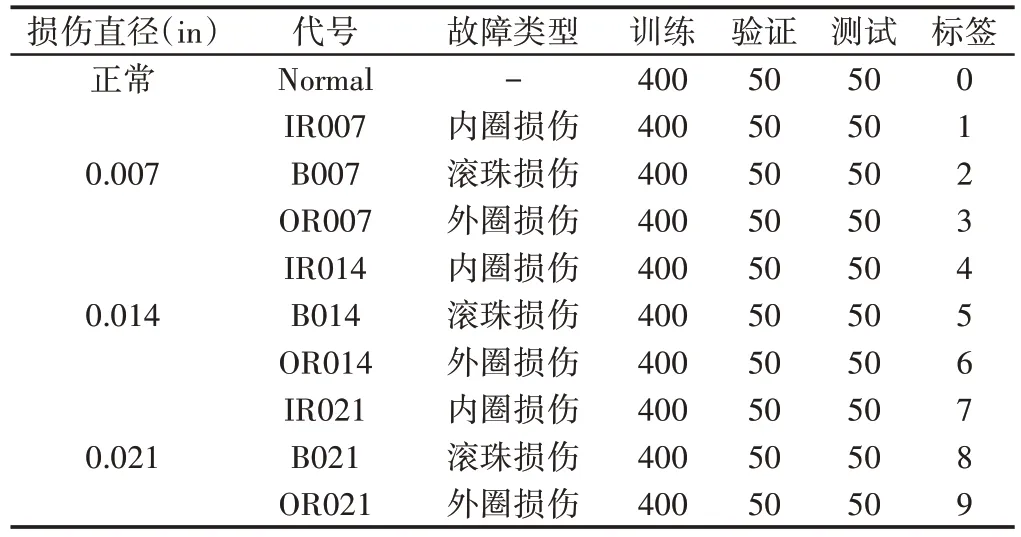
表2 实验数据集Tab.2 Experimental Data Set

5.1 模型设置

仿真实验在开源深度学习框架PyTorch下实现，为了节省内存和加快计算数据读取速度，对实验数据采用批量（batch）处理。对提出的模型在训练集上训练的同时在验证集进行验证，根据模型在验证集上的收敛情况合理设置模型超参数。

在模型没有过拟合的前提下，设置批处理大小（Batch Size）为128，Dropout层丢弃概率设置为0.5，采用多分类交叉熵损失函数（Cross Entropy Loss）作为模型训练的损失函数。为了加快训练并使模型尽可能的收敛到全局最优解，训练过程采用学习率动态调整策略，初始学习率设置为0.001，每经过10轮训练，学习率衰减为原来的0.8倍，最终经过50轮迭代学习率衰减至0.0003，学习率在训练过程中的变化，如图5所示。

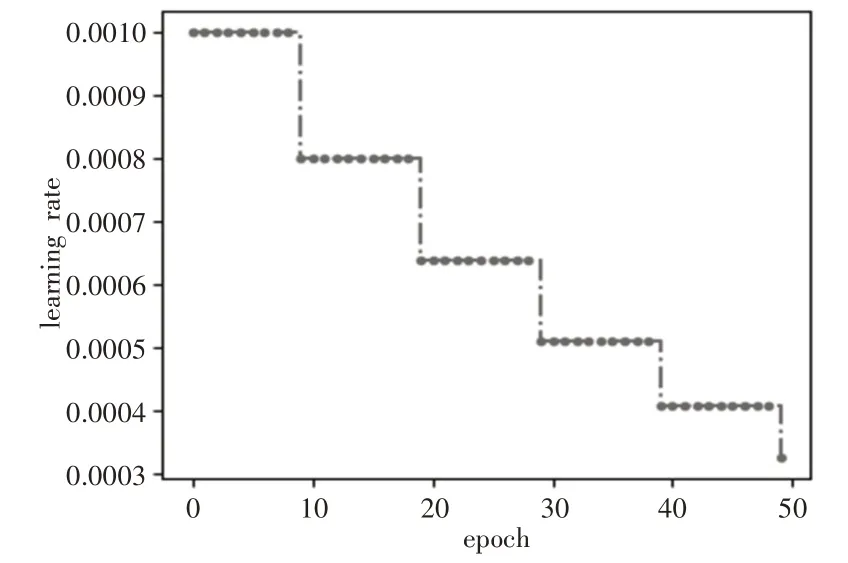
图5 模型训练过程中学习率的变化Fig.5 Changes in Learning Rate During Model Training

5.2 恒定负载下的故障诊断

为了验证CKAM-Resnet在恒定负载下的诊断性能，在电机负载为1hp，2hp和3hp的条件下分别进行实验。以负载1hp情况为例，模型在训练过程中在的训练集和验证集的误差（loss）变化曲线，如图6所示。可以观察到模型的loss曲线经过50轮左右训练基本达到收敛。保存经训练收敛后的模型，将训练集样本输入模型进行测试，得到最终故障诊断结果，为了保证结果的稳定性，在不同负载下分别对模型均进行20次实验，考虑到偶然因素可能对结果造成的影响，将经模型诊断后得到的实验结果中去掉一个最高值和一个最低值后的平均准确率作为最终测试结果。模型在负载为1hp、2hp、3hp下分别用测试集进行测试得到的混淆矩阵，如图7～图9所示。

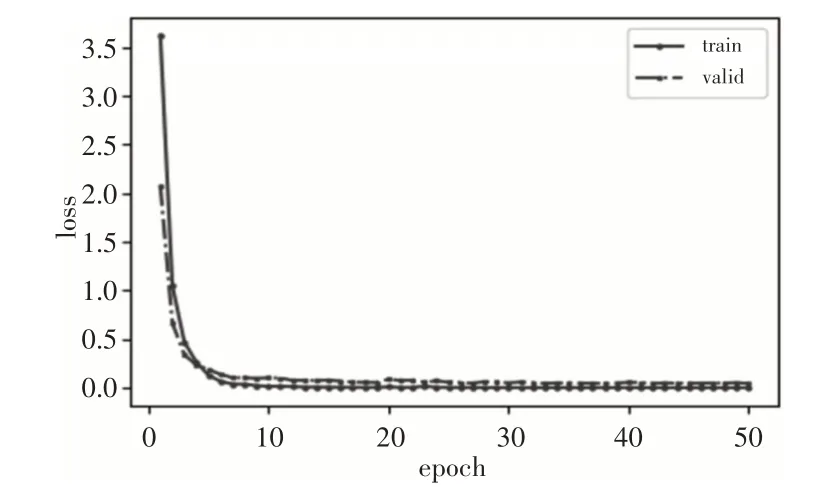
图6 模型训练过程中loss变化Fig.6 Loss Changes During Model Training

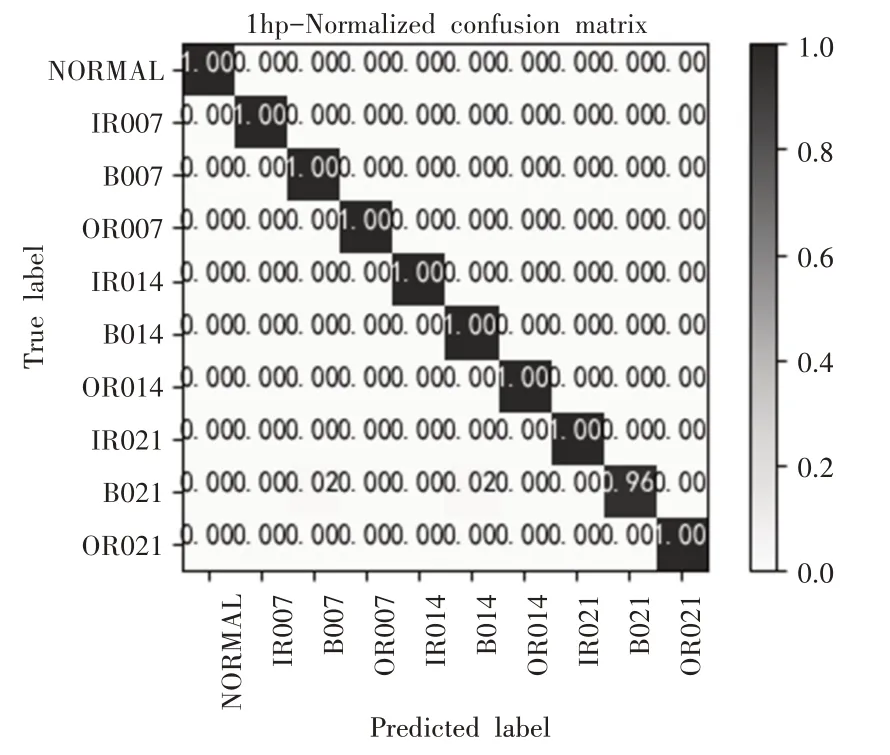
图7 负载1hp实验结果的混淆矩阵Fig.7 Confusion Matrix of Experimental Results Under 1hp Load

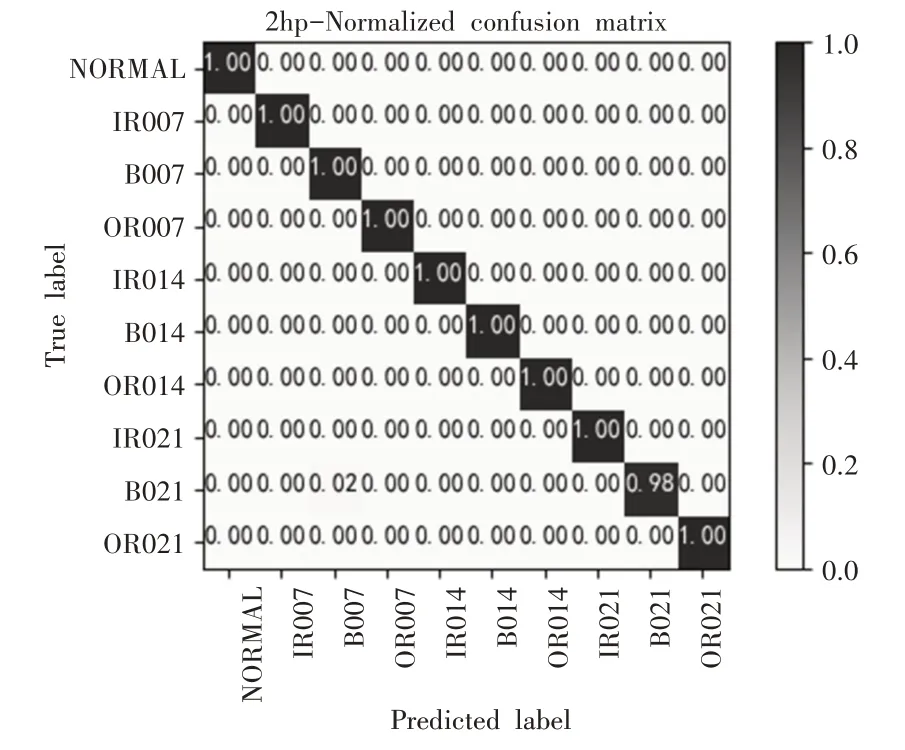
图8 负载2hp实验结果的混淆矩阵Fig.8 Confusion Matrix of Experimental Results Under 2hp Load

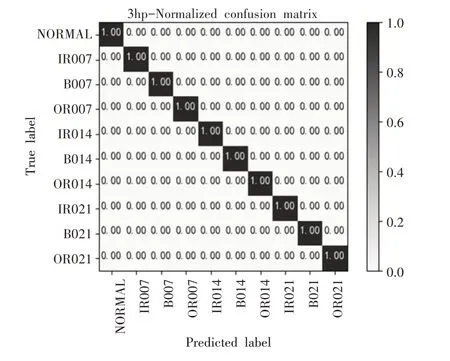
图9 负载3hp下实验结果的混淆矩阵Fig.9 Confusion Matrix of Experimental Results Under 3hp Load

Cohen’s kappa系数是一种评估模型预测结果和真实类别是否一致的指标，其值越大说明模型预测结果与真实分类结果一致性越好。同时采用Cohen’s kappa系数评估CKAM-Resnet在3种负载条件下的分类效果，其中Cohen’s kappa系数的计算公式，如式（9）所示。

p0，pe的计算公式，如式（10），式（11）所示。其中，n为待测试的样本总数，g为故障的类别总数；fij表示真实类别标签为i，预测标签为j的样本个数，fi·，f·i分别表示真实标签为i的所有测试样本个数和预测标签为i的所有测试样本个数。

经实验，模型在三种负载情况下实验得到的Cohen’s kappa系数，如表3所示。

表3 不同负载下CKAM-Resnet的Cohen’s kappa系数Tab.3 Cohen’s Kappa Coefficient of CKAM-Resnet Under Different Loads

为了验证提出方法的优越性，对比实验选取人工特征+MLP（多层感知机），EMD+SVM，MLP，LSTM（长短期记忆网络），1DCNN（一维卷积神经网络），1D-Resnet（一维残差网络）这6种故障诊断方法，其中手动特征+SVM方法选取了每段样本的时域特征（均值，方差，峰峰值，有效值，峭度，偏度，峰值因子，脉冲因子，波形因子，裕度因子，峭度因子，偏度因子）和频域特征（重心频率，均方频率，均方根频率，频率方差，频率标准差）组成的17维特征向量输入到MLP中进行分类；EMD+SVM 方法通过EMD 分解把每个振动信号样本分解为若干个IMF（本征模函数）分量，并计算各IMF分量与原始信号的皮尔逊相关系数，选取最大的4个IMF分量分别提取其时域和频域特征（与人工特征+MLP方法选取的特征一致）共68 个特征并将其输入到SVM 进行故障分类；LSTM方法采用4层结构，隐藏层神经元个数分别为256，128，64，10；MLP方法则是直接将原始训练数据和标签输入，每层神经元个数分别为2048，1024，256，10；1D-CNN，1D-Resnet采用4层结构，卷积层均采用大小为（1×3）卷积核且每层采用的卷积核数目及激活函数均与本模型保持一致，分别为8，16，32，64，每个卷层后积均接有（1×2）最大池化层，线性层神经元分别为1600，512，最后由经过Softmax层输出分10类分类结果，其中1D-Resnet则是在1D-CNN的基础上增加了短路连接。以上实验均在模型正常收敛情况下进行。经过实验得到不同故障诊断方法的故障诊断准确率（Accuracy），如表4所示。

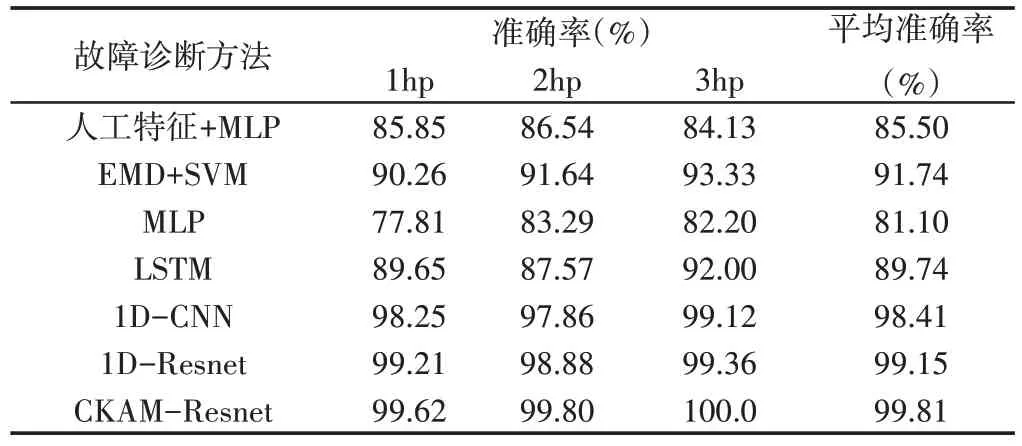
表4 不同负载下不同故障诊断方法的准确率Tab.4 The Accuracy of Different Fault Diagnosis Methods Under Different Loads

5.3 不同模型结构的可视化分析实验

为了验证CKAM-Resnet模型结构对特征提取的有效性，引入流形学习中t-SNE非线性降维方法将输入数据经过模型后每一层输出的高维特征中的冗余特征消除以留下能反映高维特征本质的低维特征，并聚类可视化以便更直观的显示模型提取到的特征的分布情况。将模型的每个SK块提取到的高维特征利用t-SNE降到二维并聚类可视化，同时与不采用SK卷积和残差结构后的模型（记作模型A）和仅采用SK卷积的模型（记作模型B），在相同位置输出特征的降维后的聚类图进行对比，如图4所示。实验选择在1hp的负载下进行，所有超参数选取策略均与恒定负载下故障诊断实验保持一致，对三种结构的模型采用同一批次的数据同时进行训练，最终三种结构的模型均正常收敛，提取三种模型在位置1，2，3处输出的特征采用t-SNE技术降维并聚类可视化的结果，如图10～图12所示。

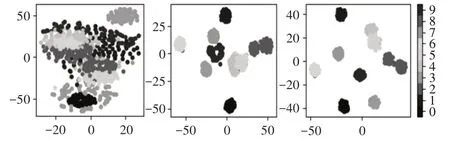
图10 模型A各层输出特征t-SNE聚类效果图Fig.10 The Output Feature t-SNE Clustering Effect Diagram of Each Layer of Model A

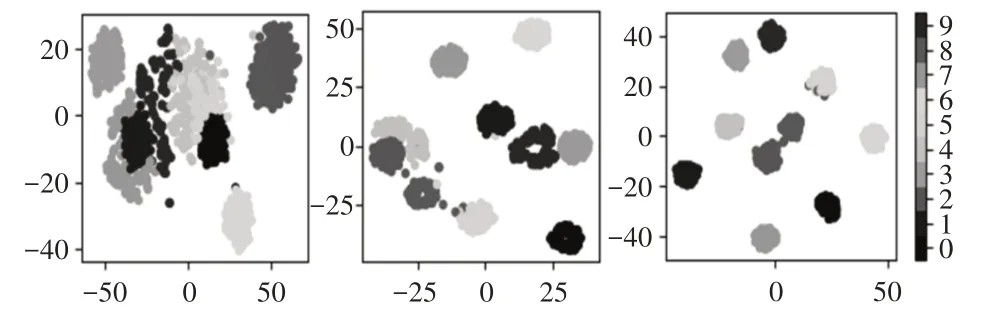
图11 模型B各层输出特征t-SNE聚类效果图Fig.11 The Output Feature t-SNE Clustering Effect Diagram of Each Layer of Model B

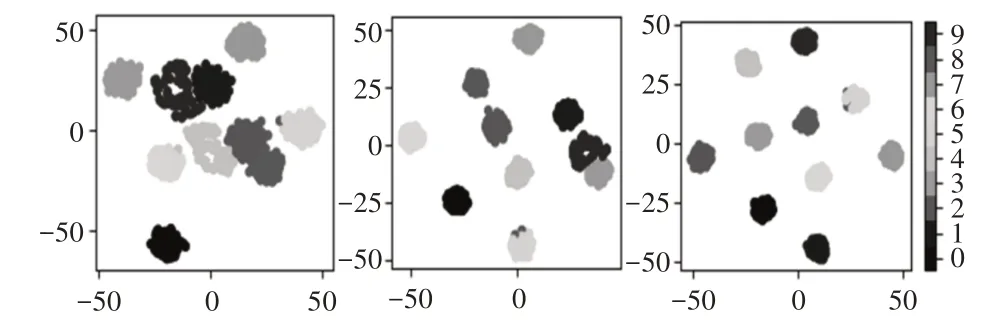
图12 CKAM-Resnet各层输出特征t-SNE聚类效果图Fig.12 CKAM-Resnet Output Feature t-SNE Clustering Effect Diagram of Each Layer

5.4 结果分析

5.4.1 恒定负载下的故障诊断结果分析

由不同负载下故障诊断实验得到的混淆矩阵和Cohen’s kappa系数可以观察到，提出的基于CKAM-Resnet模型在三种负载情况下均有着0.995以上的k值，说明模型分类结果与真实类别的一致性较好，模型在各个类别上都取到了较高的分类准确率（均达到了99%以上），每一类型的故障样本基本都被正确分类，对不同故障类型整体误判率较低。

由不同故障诊断方法的对比实验结果可以看到，CKAMResnet模型在三种负载状况下的故障诊断的平均准确率达到了99.81%，其中人工特征+MLP与EMD+SVM方法在三种负载下的平均准确率分别为85.50%和91.74%，以上两种方法都是基于特征工程，特征选取的好坏直接决定了故障诊断的实际效果。MLP与LSTM，1D-CNN，1D-Resnet作为端到端的方法和CKAM-Resnet都是直接将原始信号作为模型的输入，其中MLP方法仅达到了81.1%的平均准确率，低于人工特征+MLP方法，这是由于缺少特征工程，MLP难以直接从原始信号中提取合适的特征，而LSTM方法虽然能一定程度上利用时序信息但其特征提取能力仍弱于1DCNN，1D-Resnet以及CKAM-Resnet，在三种负载状况下仅达到了89.74%的平均准确率。1D-Resnet由于引入了短路连接，相对提升了模型综合的性能，诊断效果优于未引入短路连接的1DCNN。而CKAM-Resnet模型结合了残差结构和卷积核注意力机制，对轴承故障特征的自适应提取能力更强，在三种负载下的故障诊断的平均准确率达到了99.81%，均优于其他故障诊断方法。

5.4.2 可视化结果分析

由三种模型在位置1，2，3处提取到特征的t-SNE 降维聚类效果图上可以观察到，由于模型整体层数的加深，三种模型对故障样本的分类能力均得到了提升，不同故障类型的样本簇从混叠的状态逐渐分离，说明三种模型对故障特征均有一定的提取能力。从三种模型在同一特征输出位置的整体聚类效果来看，未采用残差结构和SK卷积的模型A最差，只采用SK卷积的模型B次之，而二者均采用的CKAM-Resnet模型最优。从聚类图上可以观察到在最后一个特征输出位置处，CKAM-Resnet基本将不同故障类型的样本簇分离，并且无论是类内紧凑度还是类间的分离程度均优于其他两种结构的模型，这说明残差结构与卷积核注意力机制的引入可以有效的增强模型在恒定负载下的对滚动轴承不同类型故障特征的提取能力，较明显的提升了最终故障诊断的效果。

6 结论

针对一般轴承智能诊断模型特征提取能力不足，提出了一种基于CKAM-Resnet端对端的故障诊断模型。采用凯斯西储大学轴承振动数据集对模型在恒定负载下的诊断性能进行实验并与其他轴承故障诊断的方法进行对比，结果表明CKAM-Resnet故障模型具有更高的诊断准确率。利用t-SNE非线性降维并将模型关键层输出特征降维并聚类可视化实验分析得到，CKAMResnet模型可以更有效提取到滚动轴承振动信号中的深层故障特征。这里仅对恒定负载情况下进行了实验并验证了CKAMResnet模型在恒定工况条件下对轴承故障诊断的可行性，但对于复杂工况条件下的故障诊断有待进一步探究。