汽车安全带锁扣惯性失效研究

郑东州，杜群贵

（华南理工大学机械与汽车工程学院，广东 广州 510640）

1 引言

汽车安全带是发生车辆碰撞时最有效的保护装置［1］，锁扣是使安全带正常发挥其约束性能的关键组成部分。锁扣失效不仅仅指其组成部件的破坏或应力屈服的材料失效，也包括在某些条件下锁扣不能完成要求的动作的功能失效。惯性开启是在使用者主动开启锁扣前不能保持锁止状态的一种功能失效［2］。因为冲击或其他因素使锁扣产生很大的加速度，从而在巨大惯性力作用下使锁扣发生开启，导致安全带约束能力减小，即为惯性失效。美国联邦机动车安全标准（FMVSS）209曾规定锁扣设计应最小化发生事故开启的可能性［3］。国内目前对锁扣失效的研究文献很少，对针对该问题进行探讨，对深入理解锁扣失效，结构改进以及新产品的开发提供理论依据［5］。

2 锁扣工作原理及惯性开启原理

2.1 工作原理

某款典型安全带锁扣结构图，如图1所示。其工作原理，如图2所示。左图为解锁状态，右图为锁止状态。

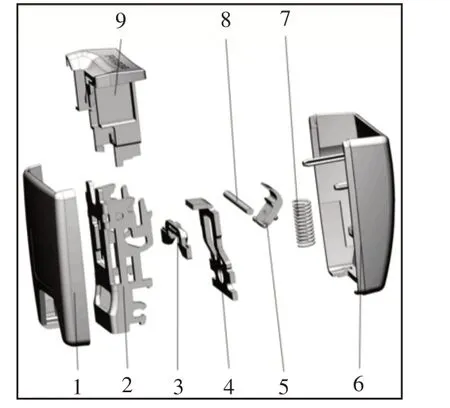
图1 锁扣结构图Fig.1 Belt Structure Diagram

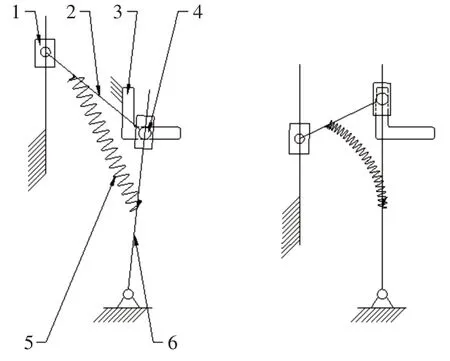
图2 机构运动简图Fig.2 Kinematic Diagram of Mechanism

锁止过程：如图2所示，锁舌推动弓形件向下运动，弹出件绕与弓形件的连接点转动，弹簧被压缩。当弓形件运动到与锁销同一水平位置并继续向下运动时，弹出件左端带动锁销向左运动，并带动锁闩逆时针转动。运动到锁销在竖直方向不受到通孔的约束时，弹出件在弹簧力作用下将锁销压到通孔的左壁上，进而锁闩顶部的勾形结构（见图1）勾住锁舌内孔。此时锁舌上的力撤去，在弹簧力的作用下，弹出件和弓形件共同上移，移动到通孔的顶部完成锁止过程，图2右侧即为锁止状态。

解锁过程：在图2 中，解锁时乘员按压按钮，按钮与锁销接触，两者共同向下运动，同时带动弹出件同向运动，弹簧继续压缩。当锁销运动到右侧无约束时，弹簧力作用使锁销向右运动，弓形件向上运动弹出锁舌，完成解锁。

2.2 惯性开启原理

通过以上工作原理分析可知，锁扣要解锁需要满足两个条件：（1）作用力值达到开启力；（2）锁销位移达到开启距离。在锁扣承受大的加速度载荷时，簧上零件的质量产生惯性力，充当开启力压缩弹簧导致锁销产生位移，由此发生开启，即惯性开启失效。

3 动力学分析

3.1 理论分析

根据锁扣工作原理及惯性失效原理分析，可建立锁扣动力学模型，如图3所示。

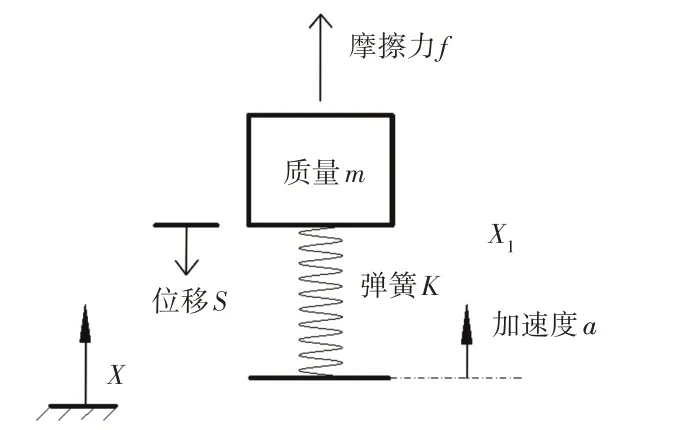
图3 锁扣动力学模型Fig.3 Buckle Dynamic Model

图3中x为相对于车辆静止的参考系，x1为固定在锁扣的参考系，选取车身为惯性空间，坐标系x作为定参考系，x1作动参考系。加速度a为锁扣加速度，位移s为质量m相对于锁扣的运动。根据运动学相关理论，质量m在x参考系下的运动为绝对运动，在x1参考系下的运动s为相对运动，加速度a引起的运动为牵连运动。牵连运动为锁扣整体的平移平移，因此质量m的绝对加速度等于锁扣整体平移加速度与m相对锁扣的加速度的矢量和，即：

在定参考系x下根据牛顿第二定律建立动力学方程：

式中：m—簧上零件零件质量；f—槽型座与锁销之间的摩擦力；s—锁销在动参考系下的位移；Fk(s) —弹簧力；sa—锁销在定参考系下的位移。

在锁扣装配体中弹簧存在预紧量，且弹簧刚度为一定值，因此：

式中：k—弹簧刚度；c—弹簧装配预紧力。

对锁销进行受力分析可得摩擦力f的表达式，锁销左右两侧分别受到槽型座和锁闩的压力，且锁闩和槽型座材料相同，即两者摩擦系数相同，锁销及锁闩受力示意图，如图4所示。

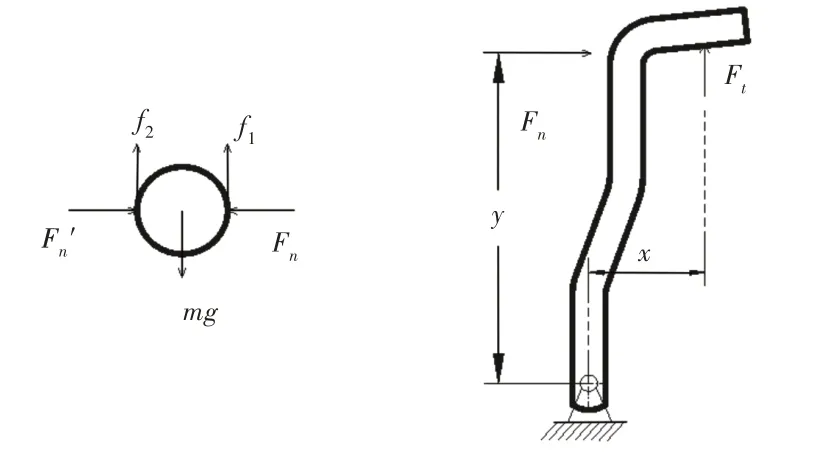
图4 锁销及锁闩受力简图Fig.4 Sketch of the Force of the Buckle Pin and the Bolt

忽略锁销自重由静力平衡可得f1=f2=Fn μ，由锁闩受力矩衡可得Ftx=Fny，因此锁销受到的摩擦力：

式中：Ft—作用在锁扣上的拉力；μ—锁销材料和锁闩材料之间的动摩擦系数，x，y，如图4所示。

将式（3）、式（4）代入到式（2）可得：

此方程为二阶非齐次线性微分方程，当a＞且为常数时动力学方程通解为：

将初始条件代入方程通解得C1=-，C2= 0，因此质量m相对于锁扣体的位移为：

上式即在锁扣受到恒加速度a作用下s随时间t的变化式。由上式可知s存在最大值，即设锁扣的开启位移为s'，smax=s'时amin=，因此当锁扣受到加速度小于amin时，锁扣不存在惯性失效的情况；当锁扣加速度大于等于amin时，加速度作用时间大于t=时会发生惯性失效。

综上所示，锁扣惯性失效与加速度波形和加速度作用时间相关，不同的加速度波形作用下锁销相对于锁扣体的运动方程不同，在加速度为恒值作用下，是否发生惯性解锁与加速度大小及加速度作用时间相关。

3.2 实例计算

根据以上分析，选取某企业生产的锁扣计算，该款锁扣主要参数，如表1所示。

表1 锁扣结构参数Tab.1 Structural Parameters of Buckle

当拉力Ft= 0时，将上表数据代入到可计算得到：

此时所需要的时间为：

因此，当该款锁扣在不受织带拉力、加速度不小于157.65g且加速度作用时间不小于9.52ms情况下存在着惯性失效风险。

为了探究加速度值对惯性失效的影响，以加速度a为x轴，时间t为y轴，锁销相对于锁扣体的位移为z轴绘制三维曲面图，如图5所示。

图5 相对位移s随时间和加速度变化图Fig.5 Surface Map of Relative Displacement

由图可知，当加速度小于157.65g时不会发生惯性失效；当加速度大于157.65g且随着加速度的增加，惯性失效所需要的时间减小。加速度与相对位移达到开启位移所需时间图，如图6 所示。由图可知，随着加速度的增大，所需时间减小，因此可知加速度值的增大会减小相应最小作用时间，但两者之间是非线性关系，在加速度增加较小时，所需要的失效时间迅速下降，随着加速度的继续增大，失效时间下降速率越来越小。

图6 失效时间与加速度关系图Fig.6 Relation Chart of Failure Time and Acceleration

根据动力学方程及其解可知，作用在锁扣上的织带拉力Ft，等效弹簧刚度k以及簧上质量m对锁销相对于锁扣体的位移具有较大影响，在Matlab中分别画出锁扣体在不同拉力作用下，在不同时间内要发生惯性失效所需的最小加速度曲线；在临界加速度情况下，弹簧刚度对锁销发生最大相对位移量及时间的影响曲线，以及不同质量情况下的临界加速度及所需时间曲线，如图7～图9所示。

图7 加速度阈值与时间、拉力关系图Fig.7 Relation Chart of Acceleration Threshold，Time and Pull

由图7可知，当作用在锁扣上的拉力越大时，发生惯性失效所需的最小加速度越大，二者呈线性关系。同时要求的最小加速度与作用时间也相关，当时间减小，所需的最小加速度增大，特别是在6ms之后，时间增大会迅速。

由图8、图9可知，随着等效刚度的增大，达到最大位移所需时间和最大移动距离都会相应减小。随着质量m增大，临界加速度减小，而达到临界加速度所需要的时间增大。

图8 临界加速度和时间与质量关系图Fig.8 Relation of Critical Acceleration，Time and Mass

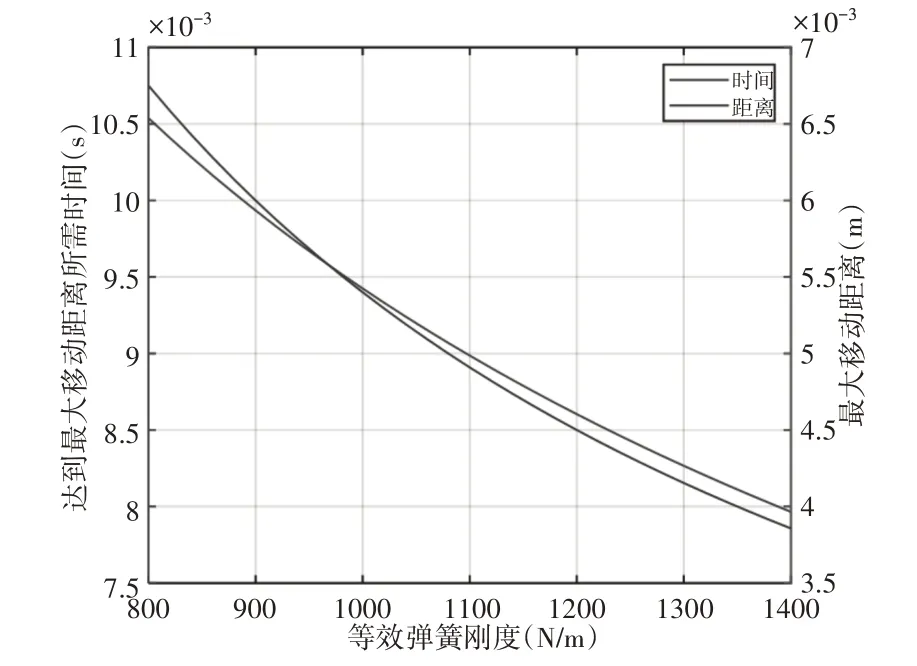
图9 时间、相对移动距离与刚度关系图Fig.9 Relation Chart of Time，Relative Displement and Stiffness

综上所述，增大织带拉力、增加等效弹簧刚度均有利于避免惯性失效的发生，而增大质量在增大加速度作用时间的同时会减小临界加速度，因此质量改变对惯性失效存在双重效果，当已知锁扣承受加速度时间较短且承受加速度较大时应减小质量，相反情况下应该增大质量。

3.3 Adams仿真验证

根据企业提供的零件三维模型，在Solidworks中进行装配并导入到adams中，建立运动副约束，基于碰撞设置接触，最后对槽型座和地面之间的移动副施加加速度驱动。设置完毕后添加锁销相对于槽型座的位移测量，通过设置不同加速度驱动值观察位移测量曲线判断是否发生惯性失效。

当加速度为1545m/s2时，相对位移曲线仿真值与理论计算值对比，如图10 所示。在0.009s 左右之前两者曲线较为吻合，在0.009s左右之后二者曲线发生了较大偏差，主要因为在0.009s左右相对位移达到了开启位移4.5mm，因此之后为惯性失效后的相对位移，adams能仿真出惯性失效后的准确相对位移值，理论计算并不能准确计算出失效发生后的位移值，对锁扣惯性失效条件进行研究，可以通过观察对比相对位移与开启位移值来判断是否发生惯性失效。综上所述，在相对位移小于开启位移阶段，所建立的动力学模型求解结果与仿真结果具有较高的一致性，证明了动力学模型的正确性。

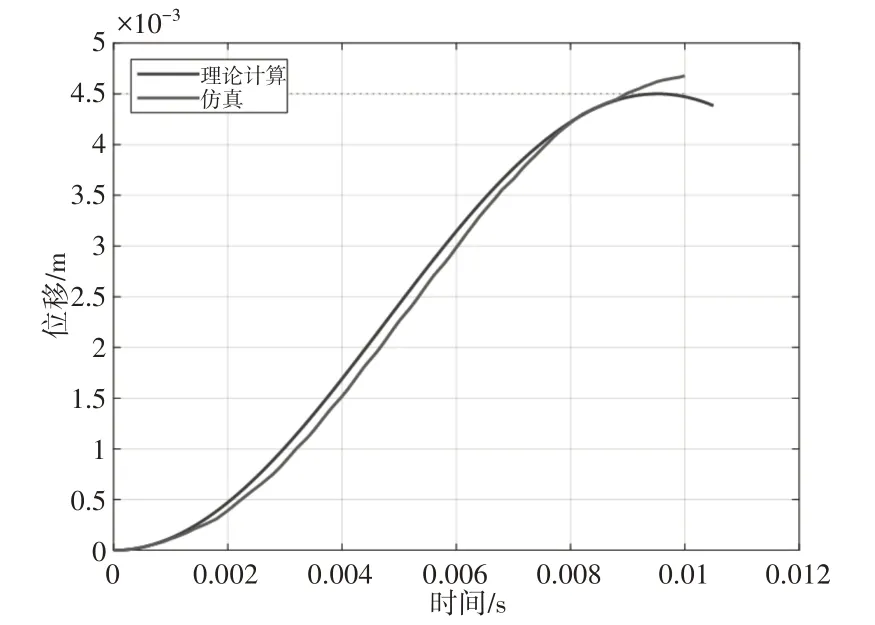
图10 理论计算与仿真对比图Fig.10 Comparison Chart of Theoretical Calculation and Simulation

4 结论

通过锁扣工作原理分析引入锁扣惯性失效的概念，对锁扣的工作过程及惯性失效过程进行了详细阐述，基于惯性失效原理和锁扣结构建立相应的动力学模型，确定了锁扣在受到恒定加速度时锁扣惯性失效判断指标。结合某款锁扣进行实例分析，确定了该款锁扣惯性失效条件及主要参数对失效发生的影响。最后通过adams仿真锁扣在加速度载荷下的动力学响应与理论计算相对比验证了理论模型的正确性。该理论模型对理解惯性失效现象的发生以及对工程人员进行产品结构改进及开发具有一定的指导意义。