双行星排HEV能量管理及传动系优化

王 敏，杨 蓉，黄 伟，张 松

（1.广西大学机械工程学院，广西 南宁 530004；2.广西玉柴机器股份有限公司，广西 玉林 537005）

1 前言

这些年，随着我国经济的飞速发展，我国汽车保有量不断增加，截至2020年6月为止，全国机动车保有量已经达到3.6亿辆，其中汽车数量为2.7亿［1］。日益增长的车辆给环境和能源造成巨大压力，汽车尾气污染已成为我国空气污染的主要来源之一［2］。此外，我国石油对外依存度已高达70.8%，天然气对外依存度达43%［3］。随着移动源污染的日益凸显以及能源对外依存度的不断升高，使得节能减排的新能源汽车成为当前的研究热点。目前受电池成本、寿命和电池污染等技术的限制，纯电动汽车和燃料电池汽车仍有较高的技术壁垒，故而，被视为低油耗乘用车的混合动力汽车日益受到重视［4］。混合动力汽车具有多个动力源，能量管理策略的设计研发是混合动力汽车的核心技术［5-7］。目前的能量管理策略主要分为基于规则和基于优化两大类［8-9］，其中，基于规则的能量管理策略具有逻辑清晰、可靠性高、易于开发等优点［10］，应用广泛，如丰田THS（Toyota Hybrid System）［11］动力系统方案，THS系统构型实用简单，但是工作模式单一，无法兼顾整个工况的传动效率。文献［12］根据所确定的发动机经济工作区进行了工作模式运行区域划分，使发动机尽可能工作在经济工作区。但没有综合考虑发动机、电机和传动系的整体传动效率。文献［13］通过反馈负载信号与电池荷电状态的实时值来控制发动机和电机的最优工作点，提高了发动机工作效率，但整车效率提高不明显。文献［14］用最优拉丁超立方体设计算法对PHEV现有传输系统进行重新设计的实验方法，优化了传动系的速比，但燃油经济性提高不大。

基于此，以国内某款混合动力公交车为样车进行研究，根据试验获得的发动机万有特性，探索基于发动机最优工作曲线的能量管理策略，合理设定动力系统的工作模式和模式切换阈值，然后采用全因子实验设计，在保证公交车动力性设计要求的基础上，以提高整车燃油经济性为目标，对传动系统中关键零部件的传动比进行优化匹配。

2 整车参数与建模

2.1 整车模型搭建

研究所采用的样车是一款双行星排混合动力公交车，整车参数，如表1所示。在AVL Cruise软件里搭建双行星排混联式混合动力公交车的整车模型，该模型包括发动机、电池组、电机、传动系统、制动系统以及联合仿真控制系统等模块，具体模型结构，如图1所示。公交车传动系统采用双行星排动力耦合结构，前行星排起功率分流作用，后行星排相当于单级减速器。发动机、电机MG1分别与前行星排P1的行星架、太阳轮相连，电机MG1主要起调速、功率分流时给电池充电的作用，通过控制b1、b2离合器的开关可实现多种工作模式。电机MG2 与后行星排P2的太阳轮相连，主要起驱动和能量回收作用，后行星排齿圈固定，前行星排P1的齿圈与后行星排P2的行星架相连，经主减速器传递动力至车轮以驱动车辆，构型简图，如图2所示。

图1 双行星排式混合动力公交车Cruise模型Fig.1 Cruise Model of Dual Planetary Row Hybrid Bus

图2 双行星排式混合动力公交车整车结构Fig.2 Structure of Dual Planetary Row Hybrid Electric Bus

表1 某型混合动力公交车样车参数Tab.1 Parameters of a Hybrid Electric Bus Sample Vehicle

2.2 双行星排动力耦合机构分析

不计行星齿轮耦合机构的内部摩擦和转动惯量时，行星排的转速、转矩关系如式（1）、式（2）所示。后行星排的齿圈固定，故转速恒为0。

式中：nS、nC、nR—双行星排动力耦合机构太阳轮、行星架和齿圈的转速；TS、TC、TR—太阳轮、行星架和齿圈的转矩；i—行星排的特征参数，数值上等于齿圈齿数与太阳轮齿数的比值。

根据发动机、电机MG1、电机MG2 与前后行星排的连接，可推算出双行星排耦合机构输出转速转矩的关系，如式（3）、式（4）所示。

式中：nout、Tout—双行星排耦合机构输出轴的转速、转矩；

ne、nMG1、nMG2—发动机、电机MG1、电机MG2的转速；

Te、TMG2—发动机、电机MG2的转矩。

根据式（3）、式（4）可知，当车速确定时，电机MG2的转速也随之确定，此时发动机的转速受电机MG1转速的影响；当整车需求转矩确定时，调节电机MG2的转矩可以使发动机工作点在理想区间内，从而发动机与车轮的转速转矩可以双解耦。

3 能量管理策略研究

3.1 控制模型结构

控制模型包括信号输入模块、需求功率计算模块、工作模式划分及需求转矩分配控制模块和信号输出模块。在Matlab中完成上述模块的搭建，然后建立整车模型与能量管理控制模型之间的数据通信，进而进行DLL联合仿真，如图3所示。

图3 联合仿真通信流程图Fig.3 Joint Simulation Communication Flow Chart

控制策略首先根据驾驶员意图，依据输入的油门踏板和制动踏板信号，参照公交车车速计算出整车需求功率，计算如式（5）所示。

式中：Pdem—整车需求功率，其值正负表示车辆处于加速或制动状态；λa—加速踏板开度；Pmax—整车所能提供的最大功率；Fb—整车制动力；v—整车车速。

将整车需求功率转化成整车需求转矩，根据实车运行工况，实时切换工作模式，在转矩分配控制模块里得到各个动力源和制动器的输出转矩指令及离合器等零部件的工作状态，最后将动力源的开关信号、负载信号、制动信号以及离合器的开关信号传递给整车模型，由此形成闭环。

3.2 基于发动机最优工作曲线能量管理策略

为了保证车辆运行时发动机工作在低油耗区，绘制了发动机最优工作曲线，如图4所示。该曲线由一系列发动机最优工作点组成，发动机最优工作点通过离散转速在发动机万有特性MAP图和等功率曲线图上插值得到。

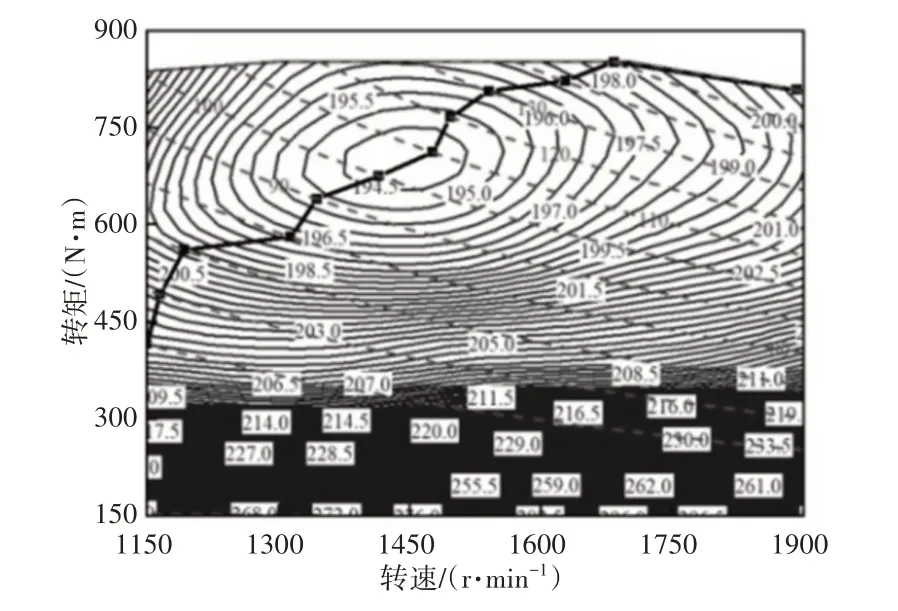
图4 发动机最优工作曲线Fig.4 Optimal Working Curve of Engine

公交车根据发动机最优工作曲线、整车需求功率Pdem、电池SOC以及车速v制定的模式划分及切换原理，如图5所示。参数说明，如表2所示。

图5 控制策略工作模式切换流程图Fig.5 Control Strategy Work Modes Switching Flow Chart

表2 逻辑门限参数说明Tab.2 Description of Logic Threshold Parameters

3.2.1 纯电动模式

当电池荷电状态在上下限区间内且整车需求功率低于发动机最优曲线的最低功率时，为了提高混合动力系统的工作效率，发动机不启动，公交车进入纯电动模式。或者当电池荷电状态高于上限值且整车需求功率低于发动机最优工作曲线的最高功率时，为了快速消耗电量使电池电量保持在上下限区间，公交车进入纯电动模式。该模式下由电机MG2单独驱动车辆，发动机、电机MG1关闭，不提供动力输出，发动机所在的行星架通过离合器b1接地锁死，电机MG1随着前行星排齿圈空转，电机MG2提供整车需求转矩。

3.2.2 混合驱动模式

当整车需求功率高于发动机最优工作曲线的最高功率且电池电量高于设定的最低值时，为了减少车辆较大负荷运行时快速消耗的电量和提高动力系统高效率运行，公交车进入混合驱动模式，由发动机、电机MG1和电机MG2共同驱动车辆。

该模式下若整车车速对应的行星耦合机构转速低于发动机最优工作曲线的最低转速时，进入低速混合驱动模式，通过控制电机MG1转矩拉高发动机转速，使发动机工作在最优曲线上，此时前行星排处于功率分流状态，发动机和电机MG2处于驱动状态，电机MG1处于发电状态；若整车车速对应的行星耦合机构转速在发动机最优工作曲线对应的转速范围内时，进入固定速比混合驱动模式，该模式下离合器b2接地、电机MG1锁定，发动机和电机MG2的转速均与车速为固定比例，此时控制发动机工作点在最优工作曲线上，电机MG2补足剩余的整车需求转矩，固定速比混合驱动模式为发动机、电机MG2转矩耦合的并联驱动；若整车车速对应的行星耦合机构转速高于发动机最优工作曲线的最高转速时，进入高速混合驱动模式，该模式下通过控制电机MG1的转矩来降低发动机转速，避免发动机工作在高速区间降低效率，此时发动机、电机MG1、电机MG2均处于驱动状态。

3.2.3 行车充电模式

当整车需求功率低于发动机高效区间的最高功率且电池电量低于电池工作区间的下限值时，或者整车需求功率在发动机高效区间范围内且电池电量在电池工作区间内时，进入行车充电模式。此时前行星排处于功率分流状态，电机MG1将多余机械能转化成电能储存在电池里。

3.2.4 再生制动模式

当整车需求功率低于电机MG2的最大功率且电池电量低于设定的上限工作阈值且车速高于进入再生制动模式的车速阈值时，整车进入再生制动模式。该模式下，发动机、电机MG1不输出动力，电机MG1 随着前行星排齿圈空转，再生制动通过电机MG2反转回收能量，再生制动是能量回收的重要途径。

3.2.5 机械制动模式

为保证驾驶员和公交车安全，不符合再生制动条件时需立即切入机械制动模式，机械制动模式可短时间输出较大的制动力矩，此时动力源皆不工作，电机MG1与电机MG2空转，公交车通过制动鼓制动。

通过控制动力源和离合器的工作状态，该混合动力系统可实现纯电动驱动、混合驱动、行车充电、机械制动以及再生制动等多种工作模式。

3.3 发动机控制

由前述内容可知，整车需求功率较大时公交车进入混合驱动模式。该模式下除了固定速比时电机MG1锁定以外，低速和高速时发动机转速与车轮解耦、与电机MG1进行转速耦合，当转矩分配控制器根据整车需求功率分配给发动机某一转矩值时，可通过调节电机MG1的转矩来调节发动机转速，进而控制发动机转矩。但是当整车需求功率较高且整车车速较低时，即使发动机工作在最优工作曲线上，公交车的燃油消耗率还是很高，因此有必要根据车速限制发动机转速工作在高效区域。

式中：ne_min—发动机最优曲线的最低转速；ne_max—发动机最优曲线的最高转速；vmin—混动模式下中低速切换时的车速；vmax—混动模式下中高速切换时的车速。

当车速v＜vmin时，为了兼顾发动机的工作效率，避免发动机转速过低，应控制电机MG1反向运转给电池充电，此时发动机转速ne=ne_min；当车速vmin≤v＜vmax时，通过离合器b2锁止电机MG1，此时发动机、电机MG2 的转速与车速为固定传动比关系，发动机、电机MG2 输出转矩耦合到传动轴，此时发动机转速ne_min＜ne＜ne_max；当车速v≥vmax时，为了防止发动机高速运转，应控制电机MG1 正向转动作为驱动电机输出动力，此时发动机转速ne=ne_max。

当整车需求功率确定时，转矩分配模块可实时分配给发动机某一转矩值，发动机转速响应较慢，通过对发动机目标转速和实际转速进行的PID 控制，得到电机MG1调节发动机工作在最优曲线上的补偿转矩，补偿转矩与转矩分配模块分配给发动机的转矩换算成的电机MG1转矩之和即为电机MG1的最终转矩，通过电机MG1可调节发动机快速达到目标转速，进而通过发动机最优工作曲线查表插值出相应的发动机转矩，PID控制流程图，如图6所示。

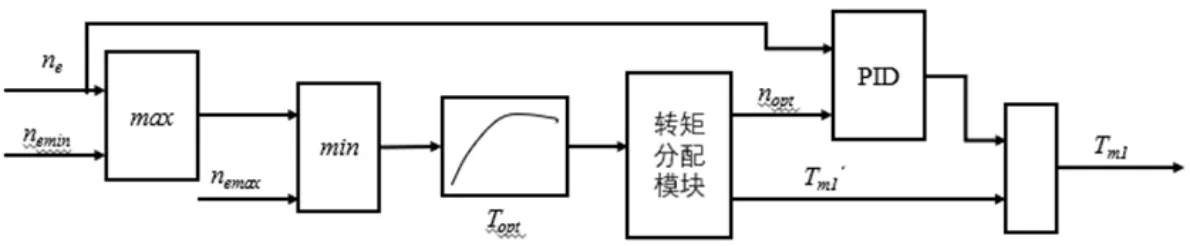
图6 PID控制过程Fig.6 PID Control Process

图中：nemin、nemax—发动机实时转速范围的上下限，可通过电机MG1的转速和车速以及前行星排特征参数确定，发动机实时转速范围的上下限计算，如式（7）所示。

4 基于全因子实验设计的传动系优化

基于发动机最优工作曲线的控制策略能够使发动机在最佳油耗区域工作，这样虽然有利于提高发动机的经济性，但是可能导致电机工作效率降低。而有效设定传动系统的传动比，有利于整车效率的提高，因此在上述能量管理策略的基础上增加全因子实验设计，对公交车传动系主要零部件的传动比进行优化，优化目标是在保证公交车动力性的基础上，提高整车燃油经济性。

4.1 优化参数及约束

选取传动系统双行星排的特征参数、主减速器的传动比3个参数作为优化参数，各参数需满足如下动力性条件。

首先需满足最高车速要求，传动系统的最大传动比满足：

其次要满足双行星排动力耦合关系，当发动机输出最大转矩时，电机MG2工作在允许转速范围内，即：

式中：neh'—发动机输出最大转矩的最高转速。

除此之外，整车还需满足车辆在爬坡等需求功率较大时的动力输出，由车辆行驶方程得：

式中：ηT—整车传动效率；f—车轮的滚动阻力系数；αm—最大爬坡度，αm= arctan(im)；im—汽车极限爬坡能力。

最后引用等效燃油消耗量作为经济性评价指标，等效油耗计算，如式（12）所示。

式中：F—整车等效油耗；Feng—发动机油耗；Fmot—电机电耗；s—油电转换系数。

式中：μ—kW·h和J的单位转换系数；H—燃油热值，取值44000kJ/kg；ρ—燃油密度，取值0.76kg/L；ηe—发动机热效率，取值0.4；计算得s= 0.27。

4.2 优化方案

根据经验值和约束条件，双行星排特征参数优化取值范围为（1.8～3）；根据动力耦合机构的约束，主减速器传动比优化取值范围为（6.08～7）；利用DOE 试验设计将每个优化参数设置5 个水平，实验因素水平，如表3所示。根据此3因素5水平表，结合全因子实验设计要求，可获得125 组实验方案。再根据式（8）～式（12）的动力性约束，对125组实验方案进行筛选，最后获得符合约束条件的27组方案，如表4所示。

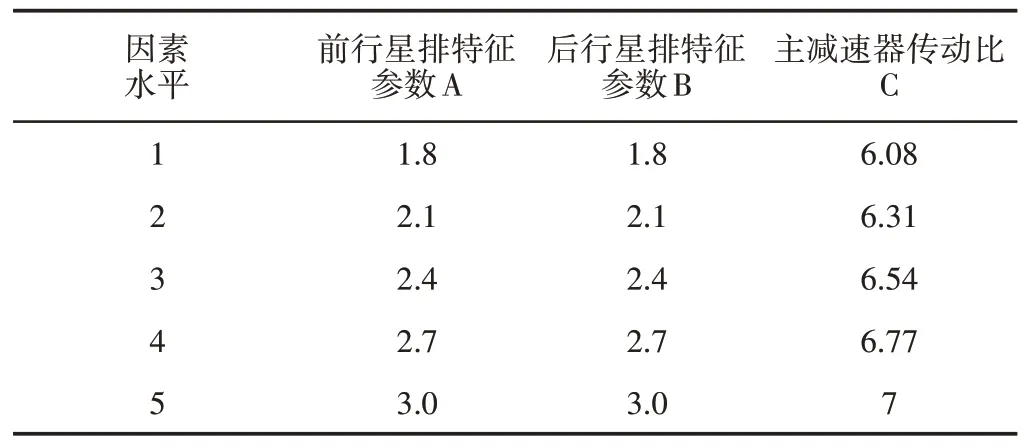
表3 实验因素水平表Tab.3 Experimental Factor Level Table

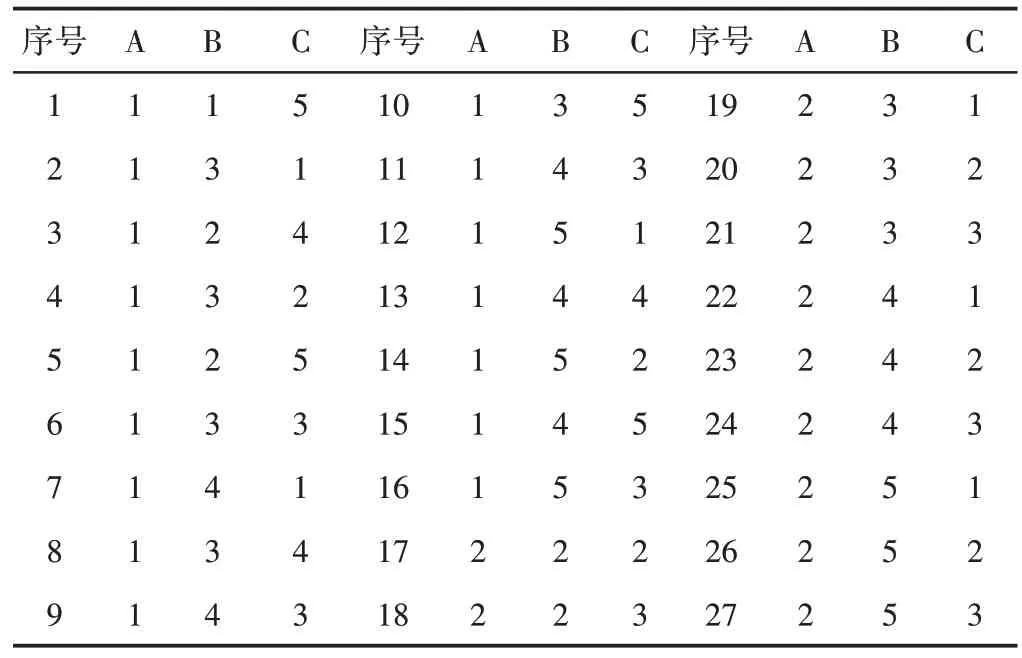
表4 实验方案表Tab.4 Experimental Scheme Table

4.3 整车仿真与结果分析

根据我国现行标准GB/T 27840-2011《重型商用车辆燃料消耗量测量方法》规定，选取C-WTVC的市区循环工况作为仿真工况，结合前文搭建的整车模型和表4所示的实验方案进行仿真结果，如表5所示。

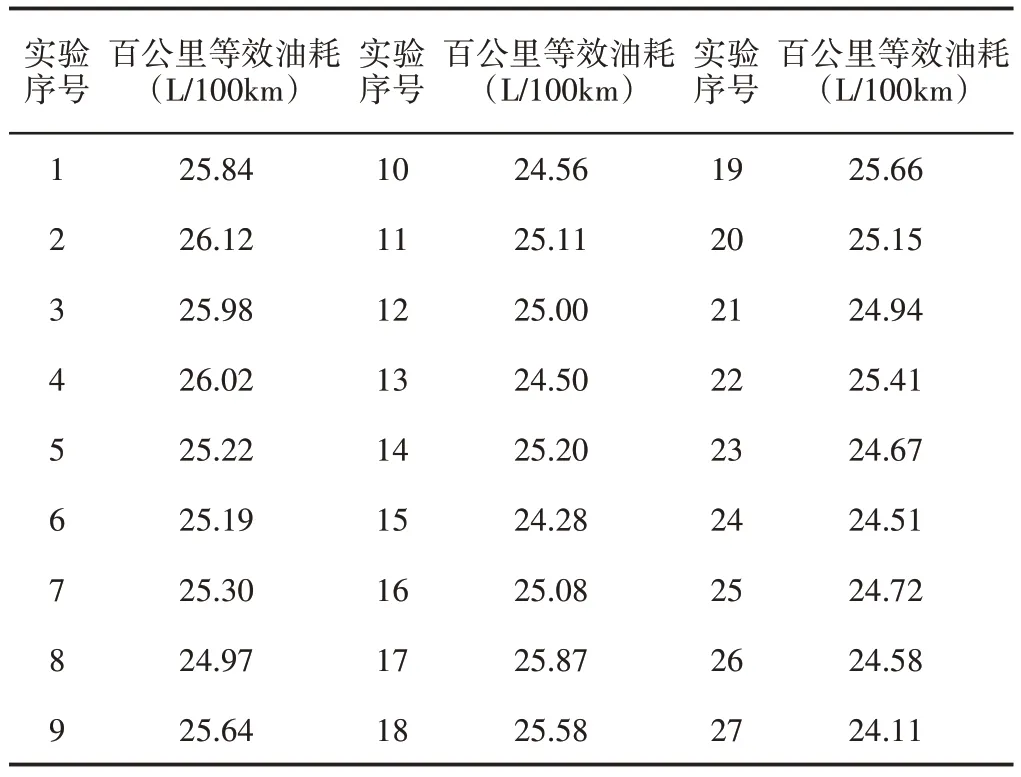
表5 C-WTVC市区循环工况下的仿真结果Tab.5 Simulation Results of C-WTVC Urban Cycle

从表5所示的结果可看出，第27组实验方案仿真结果最优，等效油耗为24.11L/100km。此时前行星排特征参数i1=2.1，后行星排特征参数i2=3，主减速器传动比i3=6.54。

优化前后发动机工作点的分布情况，如图7 所示。由图可知，发动机实际转速根据车辆的需求功率和车速以及电池电量在发动机最优工作曲线上变化，优化后发动机在中高速的工作点增多。

图7 发动机工作点分布Fig.7 Working Points Distribution of Engine

优化前后电机MG2的工作点分布情况，如图8所示。由图可知，由于电机MG2未与车轮解耦，其转速与车速直接相关，优化后电机MG2 所在的后行星排的特征参数和主减速器的传动比增大，故在相同循环工况下，电机MG2转速变化范围增大，优化后电机MG2在低速低转矩低效率区域的工作点减少，有利于提升整车效率。

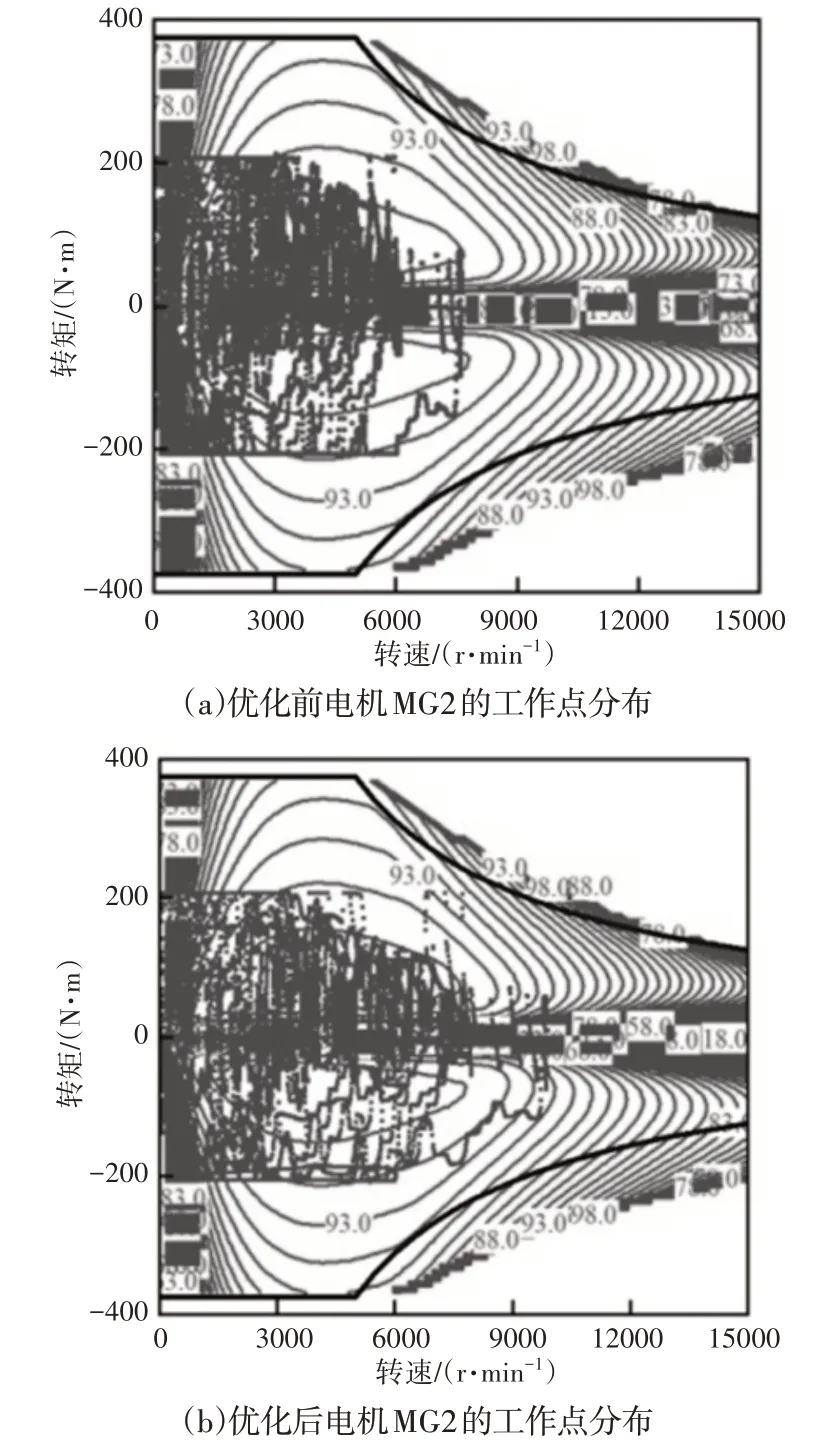
图8 电机MG2工作点分布Fig.8 Working Points Distribution of Motor MG2

C-WTVC市区循环工况下优化前后的车速跟随情况，如图9所示。由图可知，优化前后的车速重合，且与期望车速曲线基本吻合，速度跟随良好。优化前后电池荷电状态的变化曲线，如图10所示。在一个C-WTVC的市区循环工况内，电池电量有升有降，整体呈现下降趋势。优化前电池SOC从50%下降至46.84%，下降幅度为6.32%；优化后，SOC从50%下降至47.35%，降幅为5.3%，整车的电量消耗有所降低。C-WTVC市区循环工况下，累积等效燃油消耗量的仿真结果，累积等效燃油消耗量的计算见式（13），如图11所示。由图11可知，在一个C-WTVC市区循环工况内，优化前累积等效燃油消耗量为1.48L，折合百公里等效油耗为25.76L；优化后为1.38L，折合百公里油耗为24.11L，相比优化前降低约6.41%。

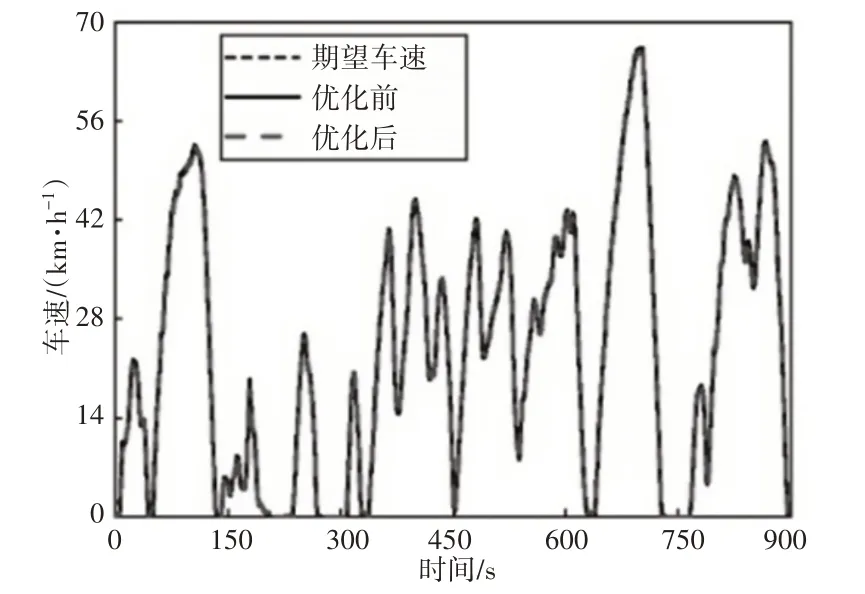
图9 C-WTVC市区循环工况下优化前后的车速变化Fig.9 Speed Change Before and After Optimization Under C-WTVC Urban Cycle

图10 C-WTVC市区循环工况下优化前后电池SOC变化Fig.10 Battery State of Charge Change Before and After Optimization Under C-WTVC Urban Cycle

图11 C-WTVC市区循环工况下累积等效燃油消耗量对比Fig.11 Comparison of Cumulative Equivalent Fuel Consumption Under C-WTVC Urban Cycle

优化前后整车的最高车速和最大爬坡度，如表6 所示。由表6 可知，优化前整车最高车速为105km/h，优化后为103km/h；优化前整车20km/h的最大爬坡度为14%，优化后整车最大爬坡度为17%。

表6 优化前后整车的最高车速和最大爬坡度对比Tab.6 Comparison of Maximum Vehicle Speed and Maximum Climbing Gradient Before and After Optimization

由此可知，采用DOE优化后的公交车与仅使用逻辑门限能量管理策略相比，优化后能使混合动力系统的发动机和驱动电机都趋向于高效工作区间内工作，从而提高整车燃油经济性。但是燃油经济性的提高，也牺牲了部分整车动力性，如最高车速。故而需要合理设置此类双行星排混合动力系统的传动比，既要满足整车的动力性能设计目标，又要结合车辆的工作特点尽量优化动力系统组成各个部件的工作区域。

5 结论

（1）以某款双行星排混合动力公交车为研究对象，研究了一套有利于发动机工作在最佳经济油耗区的能量管理策略。（2）在基于发动机最优工作曲线能量管理策略的基础上，通过全因子实验设计，对混合动力公交车双行星排的特征参数、主减速器的传动比进行了匹配优化，优化后的传动系统既保证了整车动力性能的设计要求，又显著提升了整车的燃油经济性，优化后该车在CWTVC市区循环工况下百公里等效油耗降低约6.41%。（3）基于发动机最优工作曲线能量管理策略虽然能够有效控制发动机运行在最佳经济油耗区，但是不能保证电机工作在高效率区间。因此合理设计传动比，兼顾电机工作区间亦十分重要。