基于多元回归模型的军校保障管理与课程实操程度关系研究
苏一平 赵邵蕾 牛晨伟 李承奕 李想
摘 要:为了研究军校保障管理与课程实操程度的关系,针对保障管理的各方面内容设计并使用调查问卷,使用多元回归模型和相关性分析方法研究了课程实操程度与保障管理各因素之间的关系。结果表明:保障管理与学员的学习需求匹配度、对教员教学效果的影响程度以及保障管理频率与课程实操程度均有相关性,所建立的多元线性回归模型能够应用于军校保障管理研究。
关键词:保障管理;课程实操程度;问卷调查;多元回归;显著性检验
中图分类号:G640 文献标识码:A
院校保障工作为学生在接受教育过程中提供物资、技术、设施等保障。相比于地方院校,军校的課程内容涉及实操实训更多,对应的保障内容更复杂、管理要求更高、协调难度更大,保障管理与课程实操程度之间的关系更加明显,课程实操程度越高,对保障管理工作的要求越高。为了较为直观地看出军校保障管理各方面因素与课程实操程度之间的关系,选择合理有效的数学模型是开展问题研究的关键。
近些年,国外在教育相关问题研究中采用了多元回归方法完成相关调查数据统计和分析,得到了诸多有效结论。Ben Van Dusen和Jayson Nissen针对一项物理课程教育案例提出采用多元线性回归和分层线性建模的方法,完成了112门入门级课程数据分析[1]。SilvaLugo,Jose L.等针对一项农业教育案例使用了多元线性回归模型和分量回归模型[2]。Wendan Shi
等针对一项医学教育案例采用多元回归分析评估了教育干预强度和时间对受教育人群行为的相对影响[3]。
多元回归的方法在国内教育领域也有了不少应用。参考文献[45]主要介绍多元回归方法在教育统计与信息处理中的应用。参考文献[68]使用多元回归分析的方法探寻对教育相关成效有显著影响的指标,并用这些影响因素构建出了相关的教育影响模型。参考文献[911]研究了高等教育评价的方法,利用多元线性回归构建了教学成效的预测模型。
本文使用多元回归模型来判断军校保障管理与课程实操程度之间的关系,就保障管理与学员学习需求的匹配度、对教员教学效果的影响程度、保障管理的频率等因素面向军校人员进行了问卷调查,运用皮尔逊相关分析探讨军校保障管理与课程实操程度两者之间的关联规律,进一步建立了多元回归模型,为积极推进保障管理能力建设、提高学员的实操课程成效提供方法与依据。
1 调查与分析
1.1 调查对象
面向青岛市军校人员开展了问卷调查,参与调查的人员类别有学员、教员和保障管理人员。
1.2 调查内容
首先,军校课程中涉及实操的课程较多,将学员学期中的20门有不同程度实操教学的典型课程按照普通教室教学时间、室内实验室操作学习时间和外场实作实践教学时间的占比进行了课程实操程度的计分。
保障管理工作主要会影响学员的学习效果、课堂的教学效果和教学员的使用频率。因此,调查问卷对不同课程实操程度的保障管理因素进行分析,包含了四个方面,分别是保障管理工作与学习需求的匹配度、保障管理工作对教学效果的影响程度、保障管理工作的使用频率以及学员基本信息。根据面向学员开展的保障管理内容,选择一些可量化的指标设置了问卷问题。问卷采用了5分制量表,每个部分设置了10个问题,每个问题的计分均一致,问题得分越高,表明保障管理工作与学习需求的匹配度越高,保障管理工作对教学效果的影响程度越大,以及保障管理工作的使用频率越高。
第一部分由学员填写,主要是对学员基本信息的调查,包括学员的年级、籍贯和专业。
第二部分由学员填写,主要是20门课程的保障管理工作与学员的学习需求的匹配度调查。
第三部分由教员填写,主要是20门课程的保障管理工作对教学效果的影响程度调查。
第四部分是由保障管理人员填写,主要是20门课程保障管理工作的使用频率调查。
本次调查共回收有效问卷625份,其中学员问卷516份,教员问卷97份,保障管理人员问卷12份。
2 军校教学保障与课程实操程度关系分析
为了研究课程实操程度与军校教学保障之间的关系,将保障管理工作与学习需求的匹配度、教学效果的影响程度和教学保障的使用率和其他影响因素作为自变量,课程实操程度的分数作为因变量,进行以下数据处理和分析。
2.1 皮尔逊相关分析
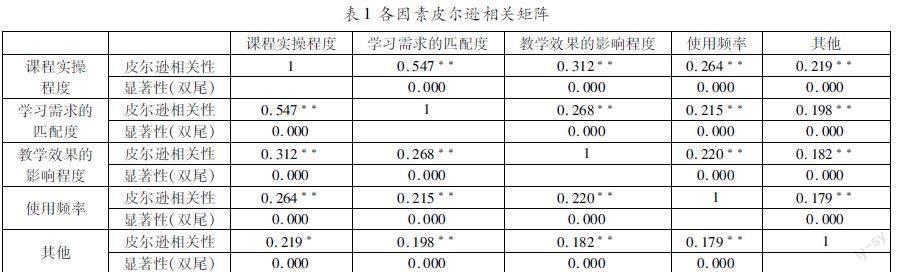
运用SPSS软件分析问卷数据,按照课程实操程度与保障管理工作的学习需求的匹配度、保障管理工作对教学效果的影响程度、保障管理工作的使用频率、其他因素之间的关系,得到各因素皮尔逊相关矩阵如表1所示。
由表1可见,保障管理工作与学习需求的匹配度、保障管理工作对教学效果的影响程度、保障管理工作的使用频率和其他因素与课程实操程度的皮尔逊相关系数R值分别为0.547,0.312,0.264,0.219。其中,保障管理工作与学习需求的匹配度和课程实操程度之间的皮尔逊相关系数R接近0.6,说明这个因素与课程实操程度存在较强的相关关系。而其他因素的皮尔逊相关系数R虽然较低,但是都达到了显著水平,可以说明课程实操程度越高,需要的保障管理工作水平就越高。
2.2 教学保障与课程实操程度的多元回归方程
经过各因素皮尔逊相关矩阵分析后,为了进一步得出保障管理与课程实操程度之间的数学关系,进行多元回归分析。由于课程实操程度与各个自变量之间存在近似的线性关系,因而选择多元线性回归分析。多元线性回归的一般数学模型为:
Y=ɑ+β1X1+β2X2+β3X3+β4X4+e(1)
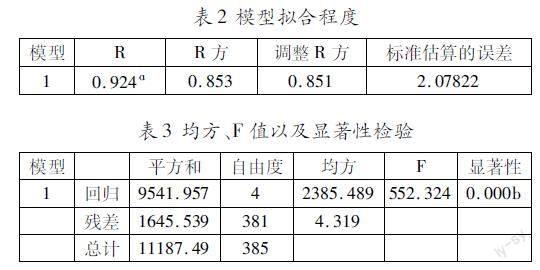
以上(1)式中:Y为课程实操程度分数;X1为学习需求的匹配度;X2为教学效果的影响程度;X3为使用频率;X4为其他影响因素;ɑ为常数项;e为随机变量。使用SPSS软件进行多元线性回归分析得到以下数据,见表2、表3。
表2列出了模型的R、R方、调整R方以及标准估算的误差,用于查验模型的拟合度。其中,R方为模型的拟合度,R方越接近于1,其反映的自变量与因变量的共变量比率越高,模型的拟合程度越好。本次定义模型所得的多元相关系数R=0.924,拟合多元线性回归的确定系数R方为0.853,调整R方为0.851,标准估算的误差为2.07822,该模型的拟合度较好。
表3用于看模型整体的显著性,模型的回归平方和为9541.957,F值为552.324,F的值比较大,且显著性约等于0.000<0.05,因此可以认为本次所建的多元线性回归方程模型有效。
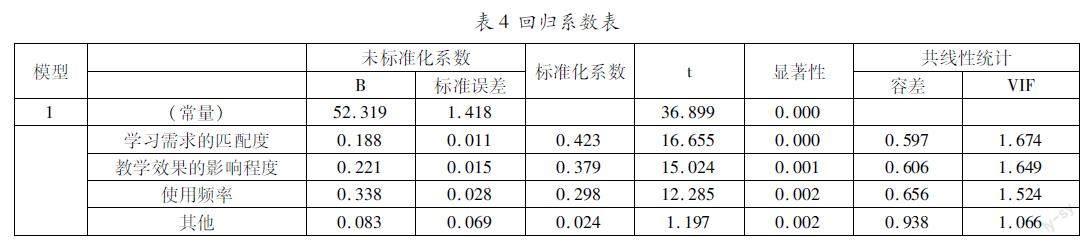
表4为该多元线性回归方程模型的回归系数表。通过共线性统计中四个自变量的VIF值均小于3,没有共线性问题。四个自变量X1、X2、X3、X4的T检验的p值分别为0.000、0.001、0.002和0.002,因此可以认为四个自变量对因变量Y均有显著影响。根据以上表中的数据可以得到相关多元线性回归方程:
如图2所示,正态分布PP图中的数据看上去近似呈现出了一条对角直线,说明数据的累计比例与正态分布累积比例基本保持一致,数据呈现出正态性。
如图3残差散点图所示,数据在残差0值上下大致呈对称分布,没有极端值出现,说明总体效果较好,无异常点,总体模型可以应用在军校保障管理工作与课程实操程度的关系研究中。
3 结论
军校实操课程的保障管理工作需要与时俱进。本文根据军校人员的调查问卷数据,运用皮尔逊相关分析发现了军校实操课程的保障管理工作的学习需求的匹配度、教学保障对教学效果的影响程度、教学保障的使用率等几个因素与课程实操程度的相关性,建立了军校保障管理工作与课程实操程度的多元回归方程,为进一步研究军校保障管理工作与课程实操程度关系的相关工作提供参考。
参考文献:
[1]Van Dusen B,Nissen J.Modernizing use of regression models in physics education research:A review of hierarchical linear modeling[J].Physical review physics education research,2019,15(2):020108.
[2]SilvaLugo JL,Warner LA,Galindo S.From parametric to nonparametric statistics in education and agricultural education research[J].The Journal of Agricultural Education and Extension,2022,28(4):393413.
[3]Shi WD,Ghisi GLM,Zhang L,et al.Systematic review,metaanalysis and metaregression to determine the effects of patient education on health behaviour change in adults diagnosed with coronary heart disease[J].Journal of Clinical Nursing.
[4]李毳毳,張智.基于SPSS的线性回归分析在教育研究中的应用[J].科技创业家,2013(22):153.
[5]于水华,郑任儿.浅谈SPSS在教育信息处理中的应用[J].电脑与电信,2006(10):5558.
[6]吕戎,巩世广.基于多元线性回归模型分析新形势下大学生心理健康教育[J].许昌军校学报,2012,31(05):1621.
[7]张新华,骆昌日,苏智.基于Logistic回归的计算机应用基础课程统考成绩分析[J].高等函授学报(自然科学版),2012,25(06):4548.
[8]陈丽妮.基于多元线性回归模型的现代农业远程教育影响因素分析[J].现代化农业,2015(02):5254.
[9]刘晓雲,刘鸿雁,李劲松.基于多元线性回归的学生成绩预测研究[J].计算机技术与发展,2022,32(03):203208.
[10]曲建民.回归分析在高等教育评价中建立预测模型的应用[J].数学理论与应用,2006(03):98101.
[11]顾金池.学生成绩影响因素分析与预测研究——基于多元回归和决策树模型[J].管理观察,2019(25):156157.
作者简介:苏一平(1996— ),女,汉族,山东青岛人,硕士研究生,助理工程师,研究方向:教研保障管理。

