基于TPS插值的改进网格弯曲变形算法

赵 鑫,石志良,袁 琼

(1.武汉理工大学 机电工程学院, 湖北 武汉 430070;2.湖北第二师范学院 计算机学院,湖北 武汉 430205)

随着三维数据采集技术的快速发展,用户可以通过扫描设备获取或使用建模软件直接生成三维模型[1-4]。在骨科外固定临床应用领域,医生采用三维扫描模型和3D打印技术制作外固定成为趋势[5]。但由于病理性等原因会出现患者骨头移位而达不到应扫描的正常位置,对受伤部位强行移正会给患者带来极大痛苦,而且可能造成受伤部位伤势加重,因此,医生需要对初始扫描的模型进行个性化的弯曲变形设计,得到满足临床诊疗要求的外固定三维网格模型。传统的三维CAD系统不具备该设计功能,因此,研究设计三维网格模型的弯曲变形算法,实现个性化的弯曲变形,具有重要的理论和应用价值。

基于径向基函数的网格变形技术在近年来得到了极大的发展与广泛的应用。Boer等[6]首次提出使用径向基函数进行网格的变形,由于不需要网格连接信息,该算法在实现上更加容易。Sastry等[7]使用薄板样条曲线(thin plate spline,TPS)的径向基函数解决插值问题,TPS的径向基函数在保持网格模型形状上具有优势,因此该算法生成了高质量的网格。Wang等[8]提出了一种基于多级子空间径向基函数算法的多步径向基函数方法,以进一步提高网格变形方法的搜索效率。测试结果表明,该方法在处理复杂几何形状的大变形问题时高效、鲁棒。Fang等[9]提出了一种新的基于笛卡尔背景网格的网格变形方法。该方法先利用径向基函数对笛卡尔背景网格进行变形,再将笛卡尔背景网格的位移代数插值到计算域中的所有网格上。由于背景网格粗糙,背景网格变形可以快速完成,该策略大大提高了网格变形的效率。此外,Morelli等[10]提出了一种利用径向基函数网格变形技术来实时模拟飞机结冰产生的移动结冰边界的方法。该方法选择多级贪婪表面点减少控制点的数量,提高插值操作的效率。近年来,学者们关于径向基函数变形的研究大都集中在提高变形效率上,忽略了变形后的精度问题。

笔者针对三维网格模型弯曲变形精度问题,研究一种基于TPS插值的改进网格弯曲变形算法。通过多次插值修正插值位移,降低插值误差,实现更精确的弯曲变形。

1 基于TPS插值的改进算法

1.1 算法概述

针对传统的TPS网格模型弯曲变形插值结果不精确,插值误差较大,造成变形不自然的问题,提出一种基于TPS插值的改进网格弯曲变形算法。首先用TPS插值对网格模型预处理,计算预处理后的插值误差,遍历所有误差值,将超过误差极限的控制点提取构成二次控制点,以二次控制点的插值误差作为插值位移进行二次TPS插值,直到插值位移误差达到误差极限时迭代终止,实现弯曲变形。其算法流程如图1所示。

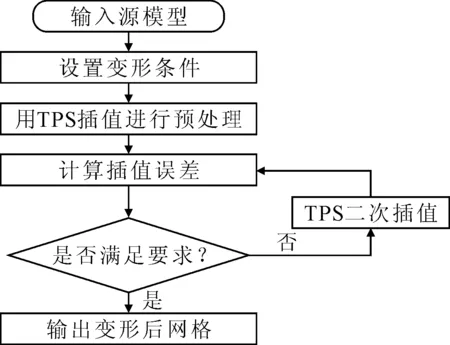
图1 基于TPS插值改进网络弯曲变形算法流程图

1.2 TPS插值方法

对于模型源控制点集{ri}和目标控制点集{ti},i=1,2,…,n,需要寻找一个光滑的函数f能满足插值条件f(ri)=ti,i=1,2,…,n,且使得f的能量E最小。

其中,

(1)

由TPS函数的性质可知式(1)存在唯一极小值,表示为仿射部分和非仿射部分的线性组合。满足该条件的基于TPS函数的整体插值函数f的一般形式为:

f(x,y,z)=p1+pxx+pyy+pzz+

(2)

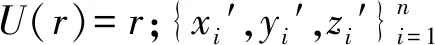
由式(1)和式(2)计算各系数线性系统:

(3)

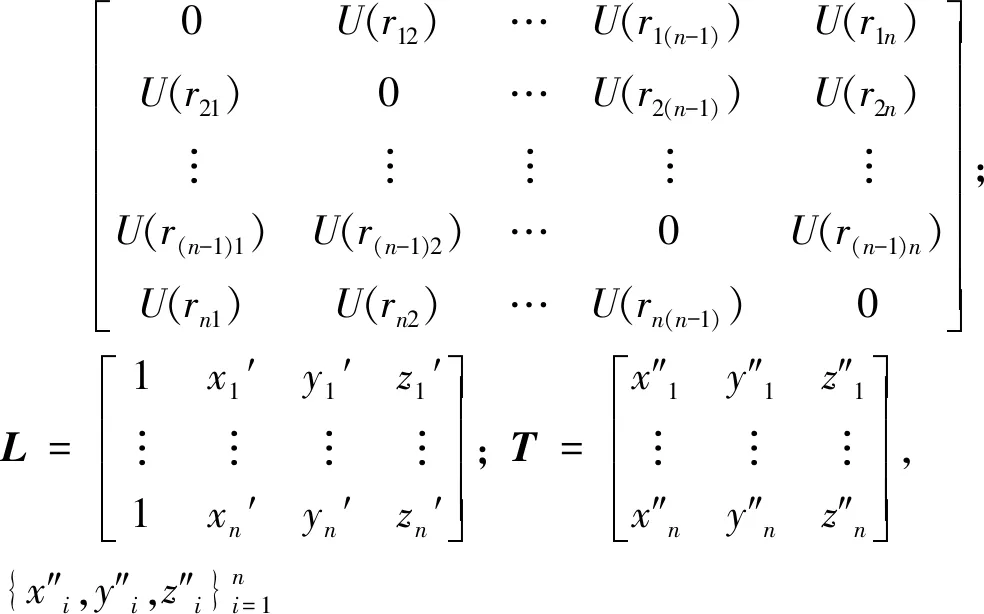
计算出式(3)中权重矩阵Q和仿射矩阵P后,描述空间中任意一点在x,y,z上的变形分量分别为fx(x,y,z),fy(x,y,z)和fz(x,y,z),可以得到插值后的顶点集合:

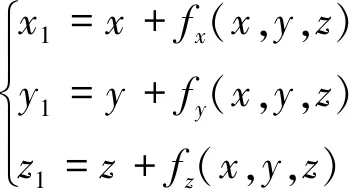
(4)

因TPS插值只是对模型顶点位置进行调整,对网格单元的拓扑关系并不做改变,只需对插值后几何位置改变的顶点集合恢复原来的拓扑关系,得到重建的预处理模型。

1.3 改进的TPS二次插值方法

由于插值的自身性质,导致模型在控制点上的插值结果精确,而在其他非控制点上的插值结果无法保证,会出现插值误差较大的情况。必然对TPS插值产生影响,如造成某些误差大的点处形状严重畸变进而导致插值效果很差,变形不自然。针对这种情况,笔者在对源模型进行TPS插值预处理后,对得到的预处理模型计算分析插值误差,得到位移量S0,以不满足插值误差极限的点为插值点,以当前点的插值误差为插值对象进行二次插值,得到位移量S1,模型上所有顶点的总位移量Ssum为:

Ssum=S0+S1

(5)

在实际情况中,算法的终止条件是插值误差达到误差极限,由于会出现多次的二次插值,因此二次插值的总位移S1为:

(6)

式中:ΔSk为第k次插值位移;v为插值次数。

在多次的插值过程中,模型中第i个顶点第k次的插值位移为:

(7)

可以得到,第k+1次的坐标为:

(8)

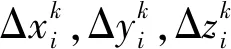
经过v次插值修正,整个模型点的最终位置为:

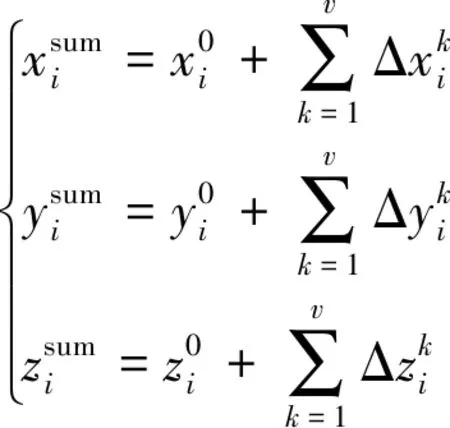
(9)

该方法的初始位移经过多次插值的修正,直到位移误差满足误差极限时停止迭代,大幅度降低插值误差,保证插值精度,避免遍历模型所有顶点的位置,提高变形的质量和效率。

2 算法实现与应用

基于Windows平台、Visual Studio开发环境、QT图形用户界面和VTK(visualization toolkit)可视化工具包,开发网格模型的弯曲变形原型系统。实验硬件设备参数为:Intel Core i7-8550U CPU@1.80 GHz处理器,Radeon 500 Series 显卡,8 G内存,Win10系统。实验的数据模型为三角网格模型,通过三维扫描仪获取原始网格数据,存储为STL格式文件,并对其进行光顺、简化和切割等预处理操作以保证网格质量,使用VTK的内部渲染引擎和可视化管道来实现模型的加载和渲染。

2.1 交互式应用

结合实际应用需求,以改进的TPS插值弯曲变形算法为核心,设计一种交互式的弯曲变形方法,使操作更加简单,变形效果更加直观可控。该方法通过选择基准点的方式生成弯曲轴信息,结合不同变形平面、变形方向和变形幅度,实现弯曲变形,可适用不同尺寸的模型。以恐龙模型为例,分别展示在不同变形平面、变形方向和变形幅度情况下的变形效果。

2.1.1 变形平面的选择

如图2所示,变形可以在XOZ和YOZ两个平面上进行,图2中深色恐龙模型为源模型,浅色恐龙模型为动态的目标模型。

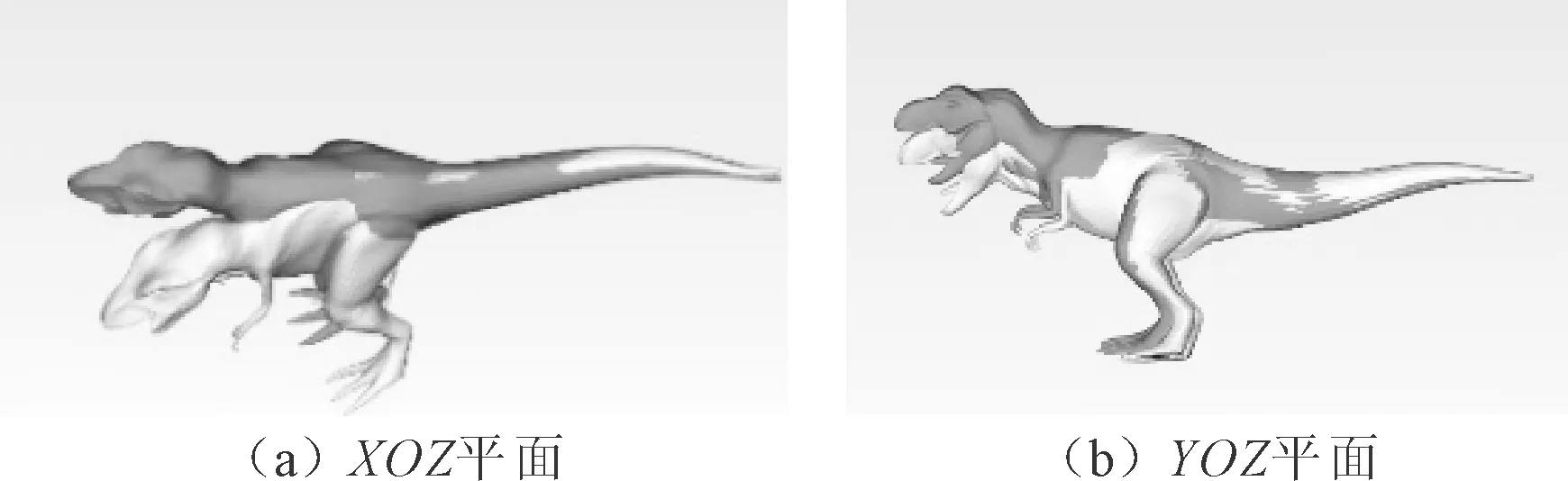
图2 变形平面的选择

2.1.2 变形方向的选择

如图3所示,变形可以个性化的选择不同的弯曲方向。图3分别为头部变形、尾部变形和同时变形的效果演示。

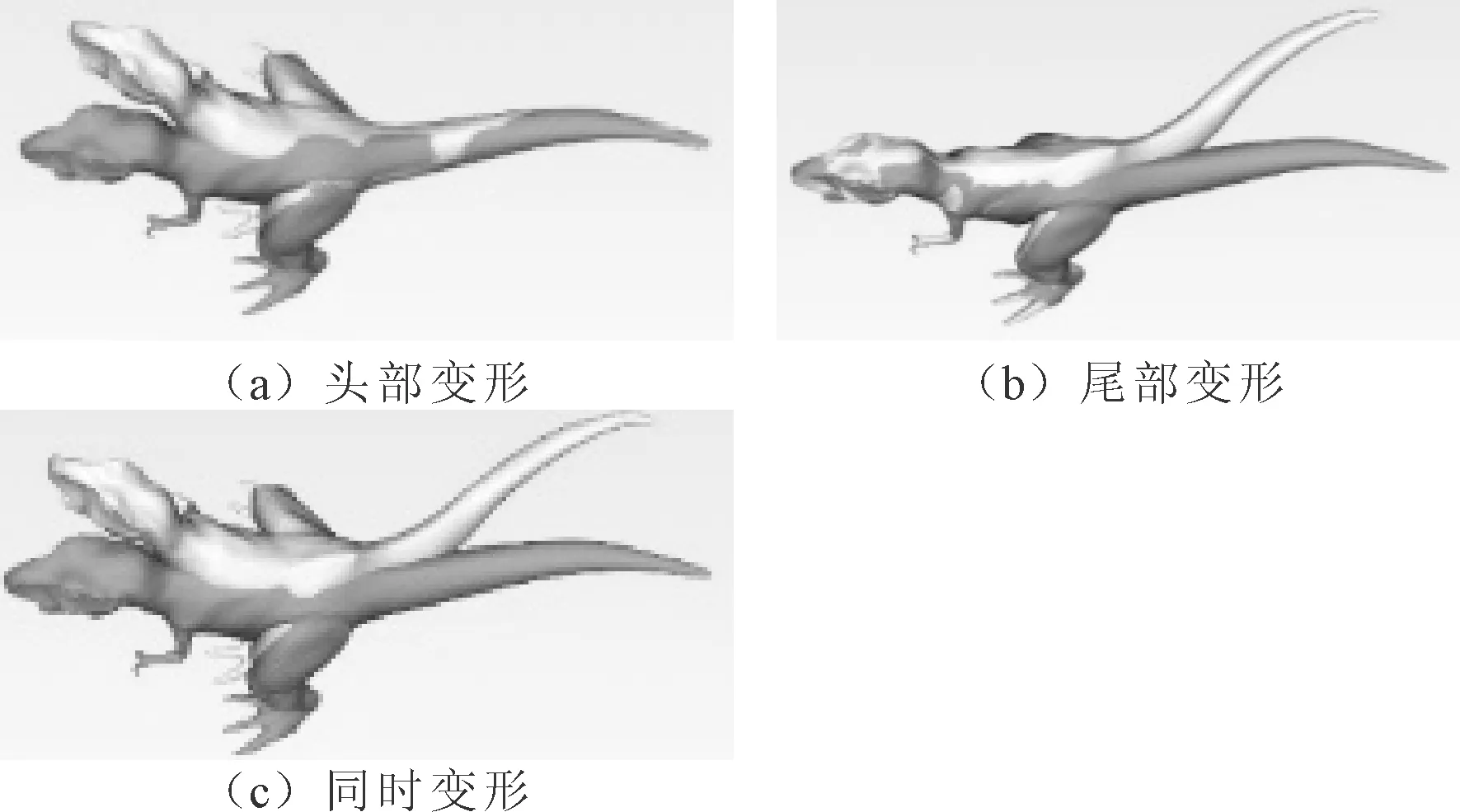
图3 变形方向的选择

2.1.3 变形幅度的选择

如图4所示,用户可以自由选择变形幅度,并能动态展现变形后的效果。图4(a)～图4(d)分别是变形幅度为-0.71、0.71、-0.28、0.28时的变形效果。

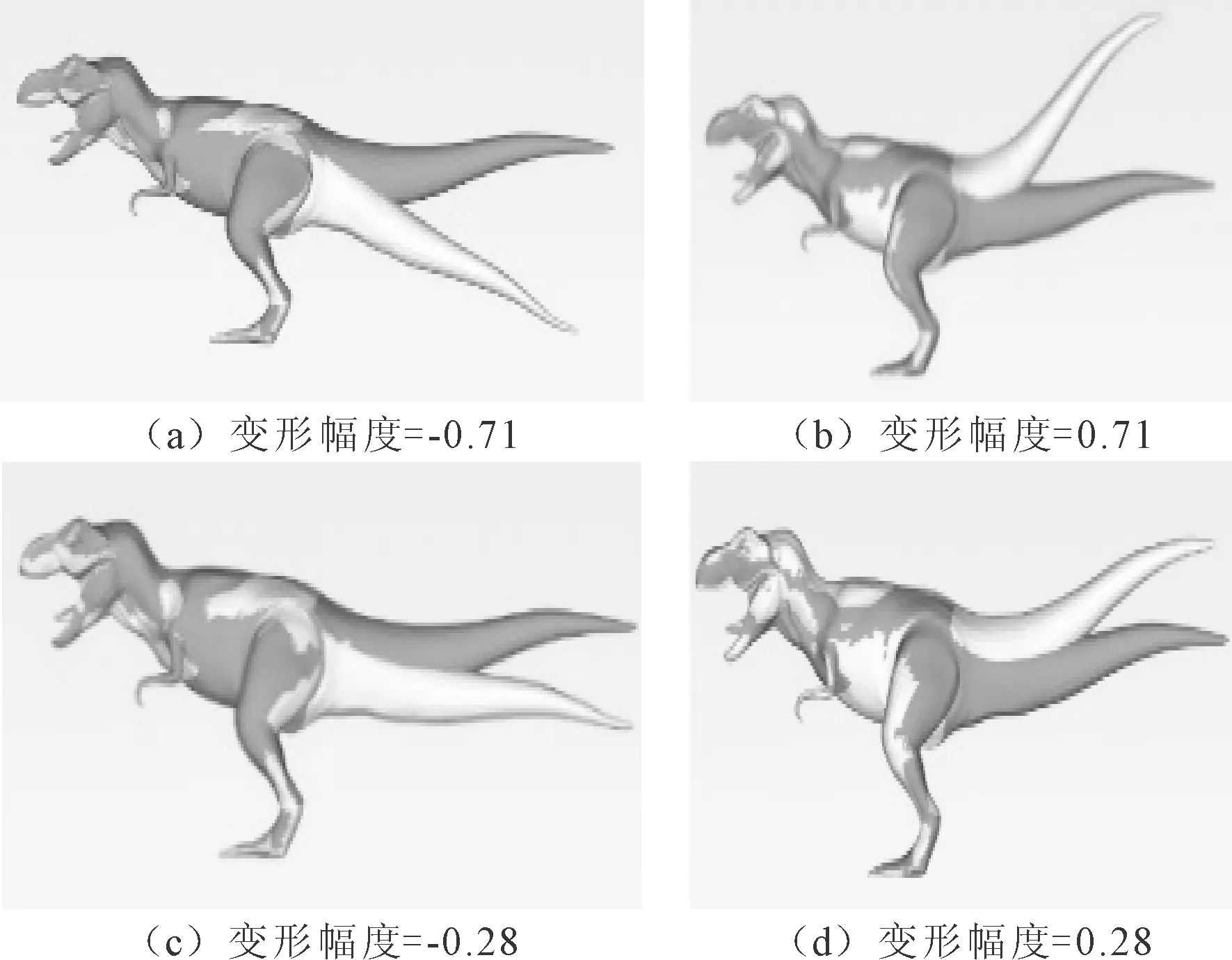
图4 变形幅度的选择

2.2 算法验证

如图5所示,采用外固定支具的踝关节模型来检验算法的准确性。三维扫描仪得到的患者踝关节模型的脚掌与地面不平行,难以支撑患者站立,需要对踝关节模型进行弯曲变形,使其脚掌与地面平行,满足实际需求。

图5 变形前后的踝关节模型

选择变形平面为YOZ平面,变形方向为头部方向,变形幅度为-0.44。图5(a),图5(b)分别为弯曲变形前和变形后的踝关节模型。对模型的插值误差进行计算分析,设置的误差极限为1e-3,迭代3次达到误差极限,得到的位移误差如图6和表1所示。在传统的TPS插值算法中,最大误差为4.332 mm,平均误差为5.745e-3 mm。在改进的TPS插值算法中,最大误差为0.997 mm,平均误差为1.419e-3 mm。并且随着迭代次数的增加,最大误差和平均误差都在降低。经过改进的TPS插值算法相较于传统的TPS插值算法,插值误差明显降低,插值精度得到提高,变形效果得到改善。

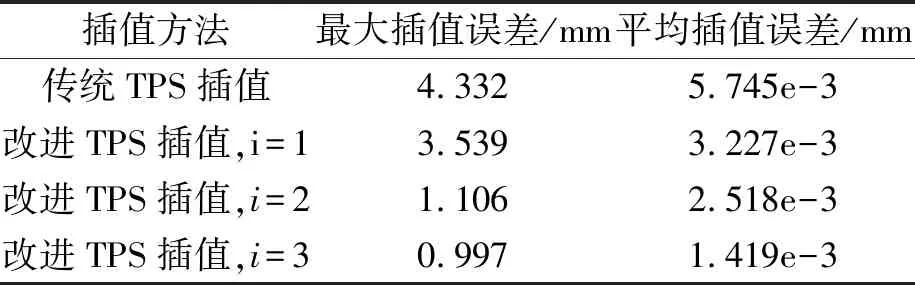
表1 不同插值方法的插值误差对比

图6 位移误差图

3 结论

笔者提出了一种基于TPS插值的改进网格弯曲变形算法,对TPS插值的插值误差进行处理,通过多次迭代插值对插值位移进行修正,使插值结果更精确。同时,本算法结合医用外固定支具三维扫描模型进行实验验证,实验结果证明,该算法稳定,变形结果精确,效果自然,同时也实现了交互式操作,降低了变形操作的难度。