基于自相关的CEEMDAN-TFPF降噪方法在齿轮故障诊断中的应用研究
李民辉,李 俊,刘 雨
(武汉理工大学 机电工程学院,湖北 武汉 430070)
齿轮作为齿轮箱的核心部件,经常受内外振动激励影响,其传动状态变的不平稳,其振动信号变成非线性平稳状态的多分量信号,传统傅里叶变换等频域分析方法不再适用[1-2]。
经验模态分解(empirical mode decomposition,EMD)方法自提出后在很多领域得到了广泛应用。然而EMD方法存在模态混叠问题,指某一个模态分量(intrinsic mode function,IMF)中同时存在其他特征的时间尺度,或者同一个或者类似的时间尺度同时出现在多个模态分量中[3]。测试信号通常伴随着强烈的噪声,对信号进行特征提取之前需要对信号进行降噪。笔者针对时频峰值滤波(time-frequency peak filtering,TFPF)定窗长降噪方法的不足提出了将TFPF降噪和自适应噪声完备集合经验模态分解(complete ensemble empirical mode decomposition with adaptive noise,CEEMDAN)相结合的联合降噪方法。
1 CEEMDAN-TFPF联合降噪方法
1.1 CEEMDAN分解基本原理
EMD可以对非平稳信号进行自适应分解获得有限个单分量平稳信号[4],但存在模态混叠和端点效应,改进的CEEMDAN分解方法可以克服上述缺点,其具体步骤如下:
步骤1首先对原信号x(t)添加N次白噪声,得到新信号x(i)(t)=x(t)+εv(i)(t),其中v(i)(t)为白噪声;ε为添加噪声的强度。对新信号进行CEEMDAN分解,分解步骤只进行到第一阶,对所得结果进行集合求平均,得到第一阶的模态分量IMF1(t)为:
(1)
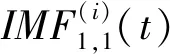
再计算信号的一阶唯一余项r1(t):
r1(t)=x(t)-IMF1(t)
(2)
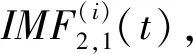
(3)
再计算下一阶唯一余项:
r2(t)=r1(t)-IMF2(t)
(4)
重复以上步骤,一直计算到最后求出的余项rk+1(t)满足单调性准则或者幅值小于设定值时分解结束,则原信号可表示为:
(5)
该方法在每一阶模态分量分解过程中都添加一个自适应的辅助高斯白噪声,降低模态混叠的影响,减小分解的重构误差,提高分解的完备性。
1.2 TFPF时频峰值滤波降噪
时频峰值滤波的本质是一种基于Wigner-Ville分布(Wigner-Ville distribution,WVD)的瞬时频率估计方法[5]。WVD定义如下:
(6)
式中,x*为x(t)的共轭复数。
TFPF方法是将含噪信号调制成一个解析信号并求出其PWVD(pseudo WVD)分布,将其峰值当作瞬时频率估计值,得到时域信号的无偏估计来消除随机噪声[6]。假设含噪信号的表达式为:
s(t)=x(t)+n(t)
(7)
式中:x(t)为不含噪的纯净信号;n(t)为噪声;s(t)为含噪的测试信号。
TFPF滤波降噪方法首先将采集的信号s(t)通过频率调制得到解析信号,再根据解析信号的PWVD峰值恢复有效信号,以此来消除噪声。将含噪信号s(t)看作是一个调频信号的瞬时频率,对信号s(t)进行调制解析,其解析信号z(t)为:
(8)
式中,μ为调频因子,取值范围为[0,1]之间[7]。
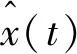
(9)
1.3 基于自相关的CEEMDAN-TFPF联合降噪方法
信号自相关函数可表征信号不同时间幅值的相关程度[9]。信号x(t)的自相关函数Rx(τ)定义为:
(10)
式中:τ为自相关函数的时延量。
由白噪声的统计特性可知其相关函数在原点处取得最大值,远离原点时快速衰减,其数值接近于零。对于含噪声较多的信号亦是如此。对于低噪声信号,其自相关函数在原点取得最大值,但在远离原点时衰减慢且呈现一定的周期性。基于此特性可以通过对每个IMF分量进行自相关分析,同时辅以方差分析,由此来判断每一阶IMF的含噪程度,以此设置分界值对IMF进行判别区分[10]。对含噪较高的IMF分量进行TFPF滤波降噪。最后将降噪后的模态分量和无需处理的模态分量一同重构得到本文方法的降噪信号。算法计算过程为:
(1)对原始信号采用CEEMDAN自适应的分解得到一系列IMF分量ci(t);
(2)计算所有模态分量的自相关函数Ri(τ)=E[ci(t)ci(t+τ)],Ri(τ)为第i个IMF分量的自相关函数;
(3)计算所有自相关函数的方差值,通过方差来确定各个分量的含噪程度。方差小于分界值的即为噪声主导的分量,反之则为有效信号分量。以此来区分IMF分量ck(t);

(5)将信号重构得到最终降噪信号:
在高中物理教学中,教师们经常会碰到学生的学习情绪不稳定、学生成绩时上时下的现象.这是由于学生在物理学习的过程中遇到困惑或者是失败造成的.教师在物理教学的过程中应该时刻关注学生学习情绪的变化,帮助学生们不断地获得成功的学习经验,有利于建立他们的自信心,对物理学习保持高涨的情绪.教师在备课过程中,要结合学生实际的学习情况选择相应的教学内容,切不可为了教学进度而忽略学生的学习进程,选择适度的作业和试题,做到因材施教,让学生尝到学习物理成功的乐趣,树立学生的自信心.
(11)
式中,R(n)为残余分量。
由于CEEMDAN算法在分解过程中添加了辅助白噪声,导致分解得到的IMF分量会含有一些残余噪声,若直接舍去前几阶分量,则会损失有效信号。TFPF降噪算法由于窗长影响降噪效果,导致算法很难在噪声抑制和信号保真两个方面做出较好平衡,把EMD分解和TFPF降噪方法结合使用,EMD可以对信号进行自适应分解得到一系列单分量信号,再通过TFPF对分解得到的IMF分别使用不同窗长进行滤波降噪处理,对于低阶的高频分量可以使用长窗长使噪声抑制效果最大化,对于低频的高阶IMF分量则不采取降噪处理。该方法可以通过对自适应分解得到的IMF进行不同窗长的处理,可以同时发挥出两种方法的优势,使降噪信号在信号保真和噪声抑制方面同时达到最优效果。
2 仿真分析
为了验证所提出的降噪方法的可行性,采用人为设置的多调制源的模拟信号来对其进行仿真验证。信号的采样频率为8 000 Hz,仿真信号的表达式为:
x(t)=[1+2cos(2πfn1t)+3cos(2πfn2t)]·
cos(2πfzt)+v(t)
(12)
式中:调制频率fn1和fn2分别为20 Hz和25 Hz;载波频率fz为300 Hz;v(t)为白噪声。
仿真信号的时域波形如图1所示。
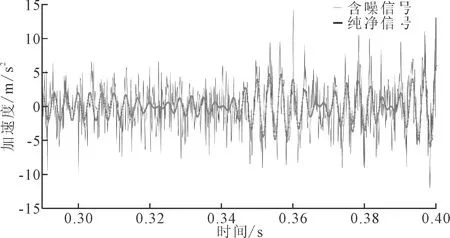
图1 模拟信号与含噪声信号时域波形
首先,通过CEEMDAN方法对加噪模拟信号进行分解,得到分解结果如图2所示,其频率范围由高到底排列。计算所有模态分量的自相关函数及其方差值,如图3和图4所示,并根据方差值的大小排序对IMF进行分类。
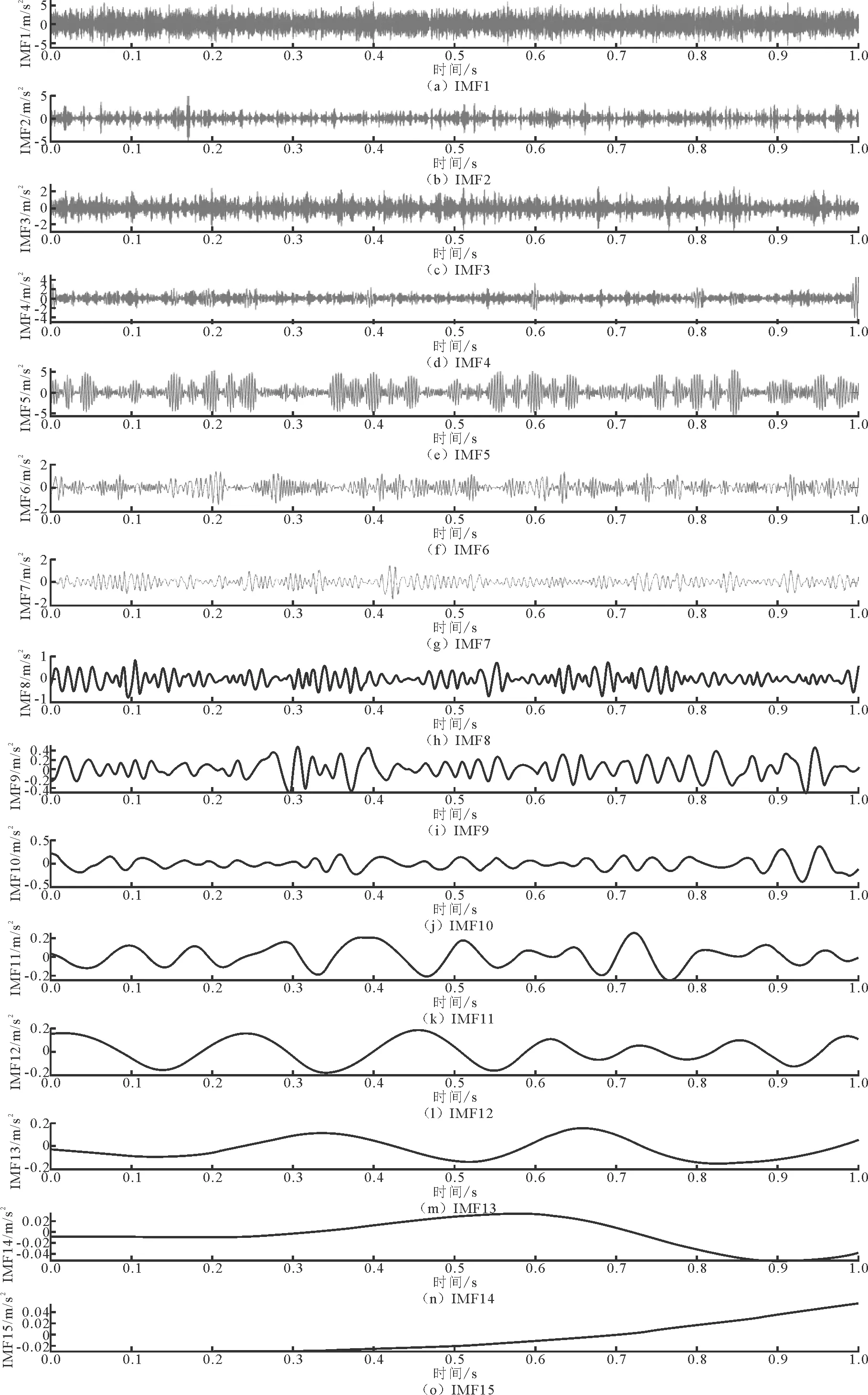
图2 CEEMDAN分解结果
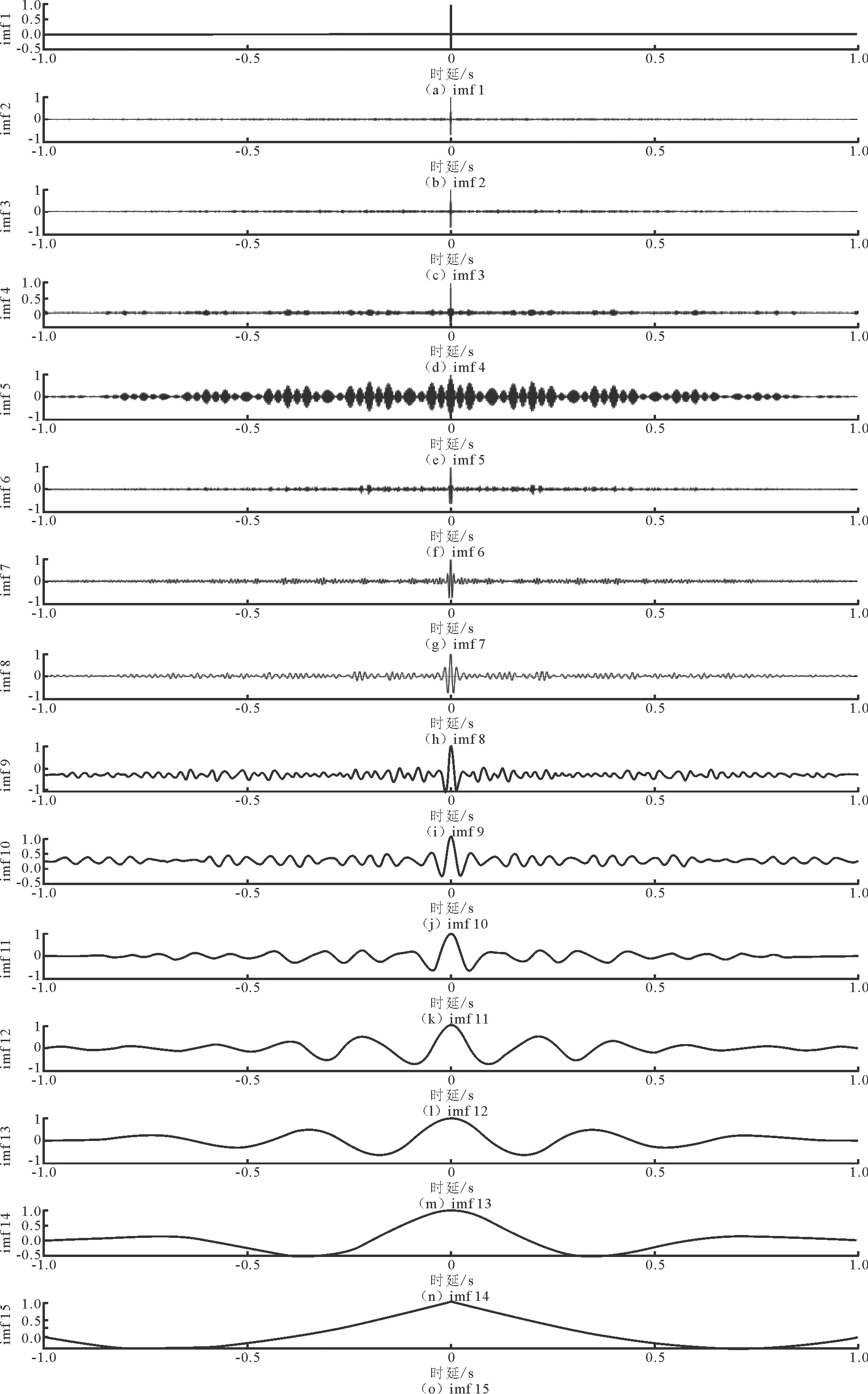
图3 各阶IMF自相关函数
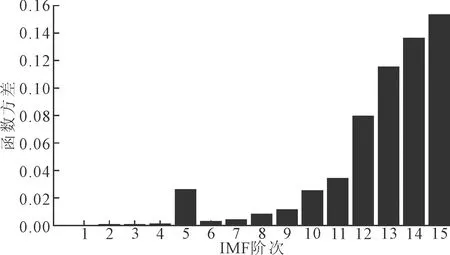
图4 各阶IMF分量的自相关函数方差
根据TFPF算法的特性,对不同的IMF分量选择不同的窗长进行滤波降噪处理,将IMF根据自相关的方差值分成3类,对第一类方差值小于0.005且频谱能量分散的分量,采用长窗长TFPF进行降噪处理,取为1~4阶和6~7阶;第三类方差值大于0.02的分量则暂不进行降噪处理,直接保留,取为第5阶和10~15阶;对于剩下中间的第二类分量采用短窗长进行处理。
各阶IMF及其降噪后的结果如图5所示。窗长较长可以更好抑制噪声,但是会损失一部分原始信号的幅值。窗长较短噪声抑制能力差,但有效信号幅值不被削弱[11]。最后将降噪后的模态分量与剩余未经处理的模态分量累加进行重构,得到联合降噪方法的最终结果。将联合降噪方法的结果与传统TFPF方法降噪结果对比,结果如图6所示,所提出的降噪方法可以有效地将含噪信号恢复成有用信号,没有过多的残留噪声,有用信号的幅值衰减也相对较少。
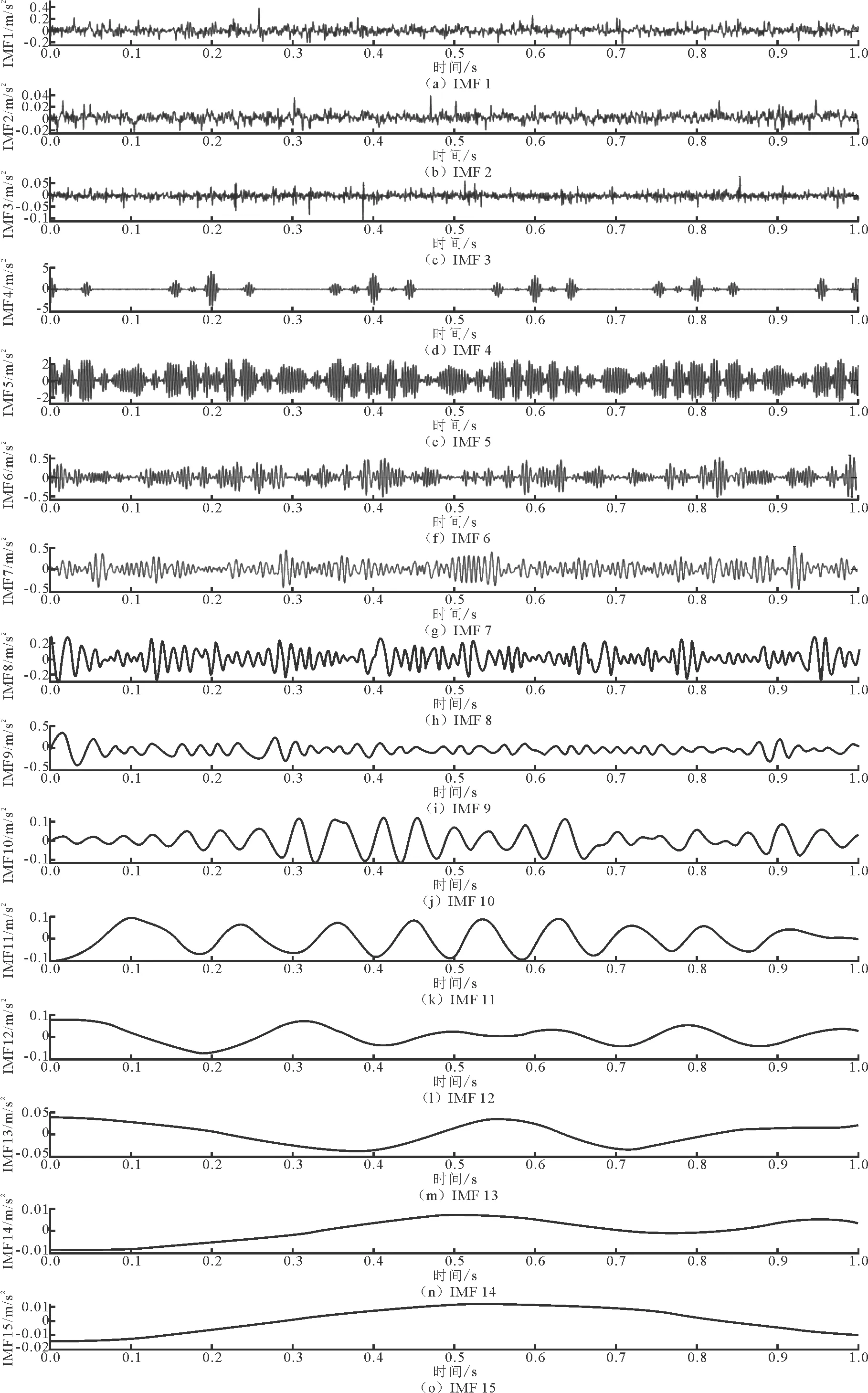
图5 各阶IMF处理后结果
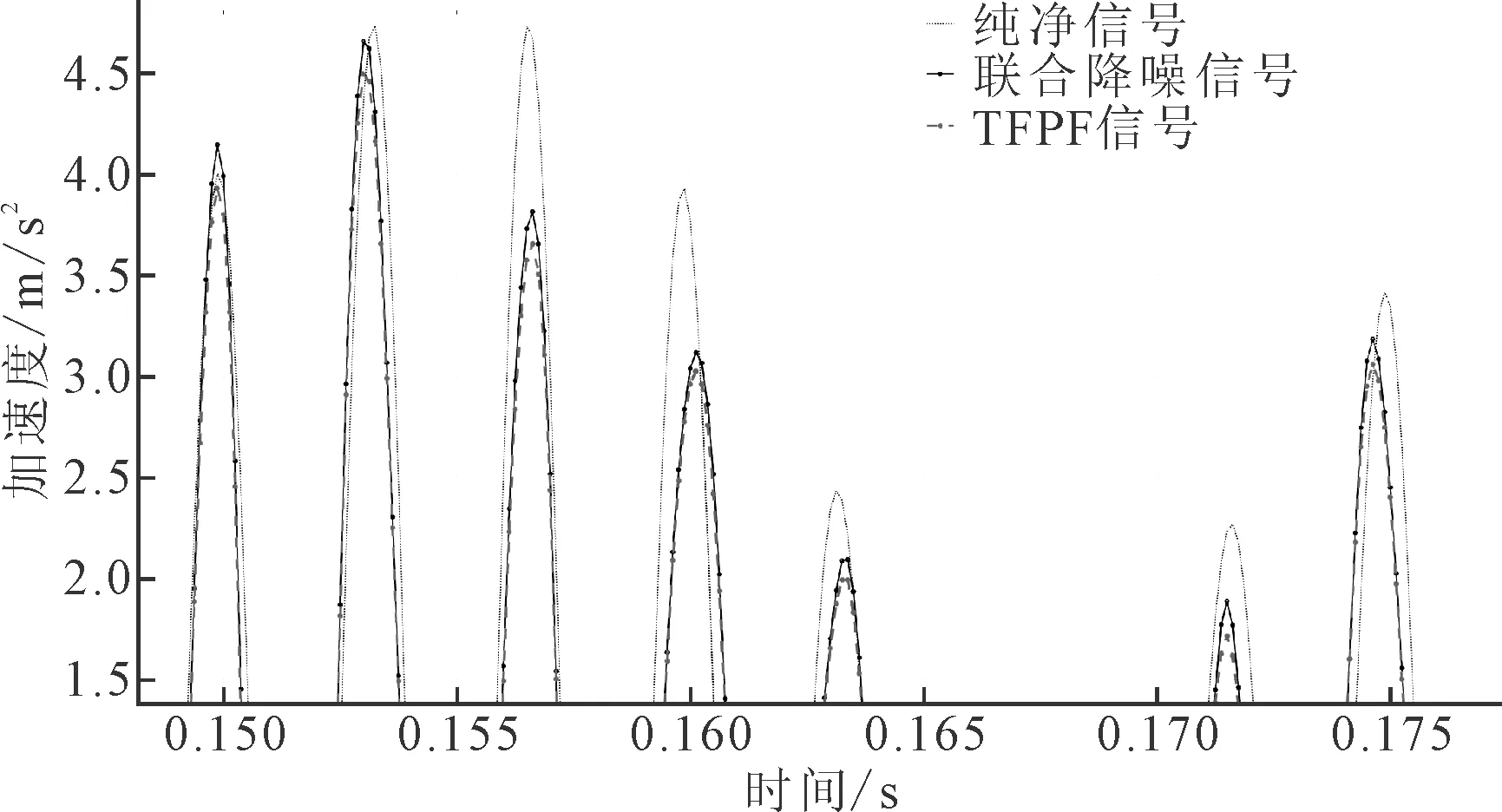
图6 联合降噪与传统TFPF降噪结果对比
为了验证所提方法的降噪性能,一般采用信噪比(signal noise ratio,SNR)和均方差(mean squared error,MSE)两个指标进行对比分析[12]。分别采用低噪声的信号和高噪声的信号进行对比分析,计算了传统TFPF方法和联合降噪方法的信噪比和均方差,对比结果如表1、表2所示。从表1、表2可知,所提出的基于自相关的CEEMDAN-TFPF降噪算法得到的信噪比优于传统TFPF方法,且降噪后信号的均方差也更小。对降噪后信号作频谱分析,如图7所示,降噪后的信号可以识别出300 Hz等特征频率。
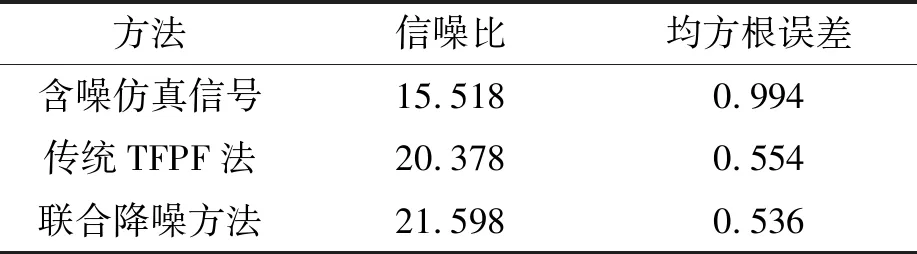
表1 低噪声时对比传统方法降噪效果

表2 高噪声时对比传统方法降噪效果
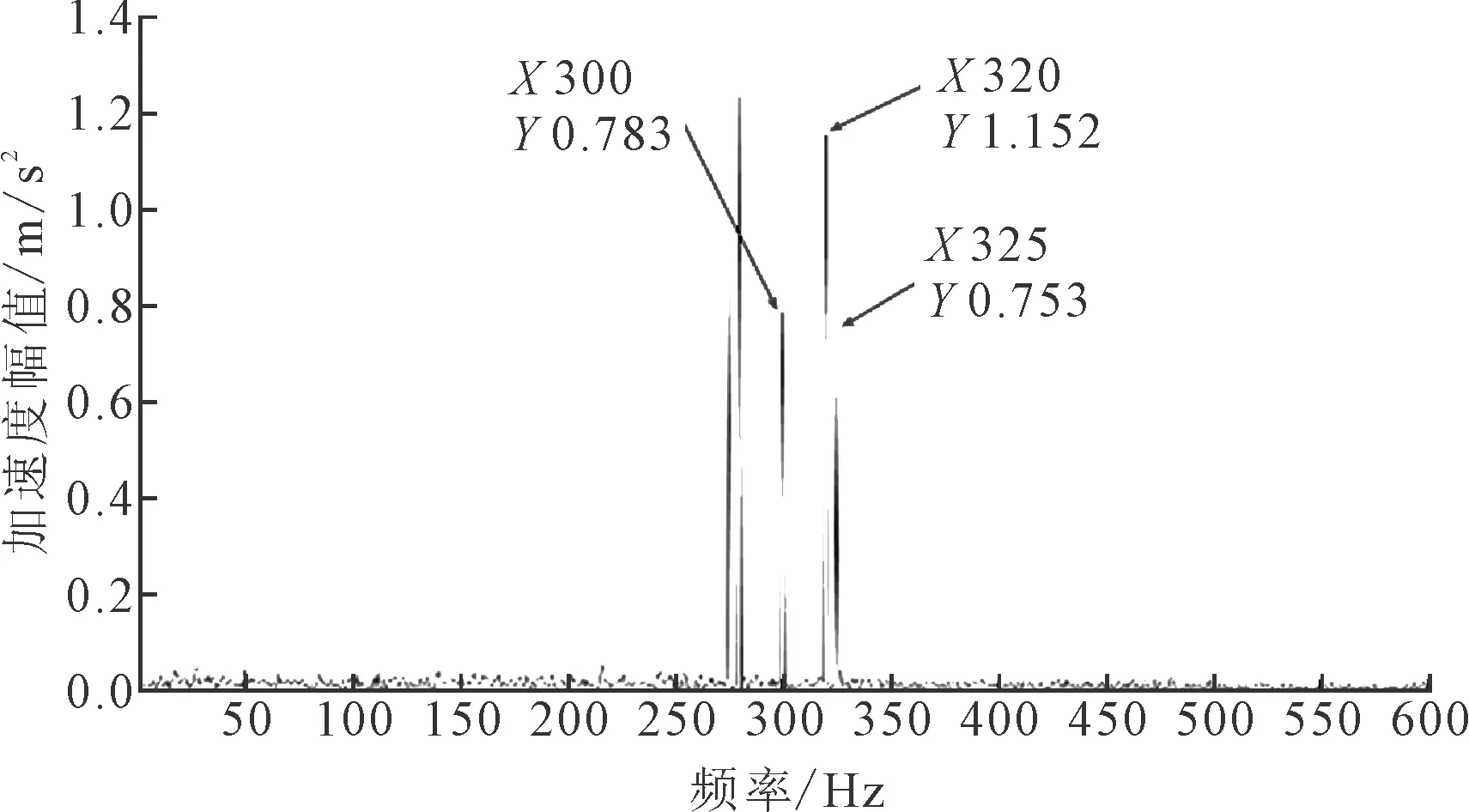
图7 降噪后信号的频谱图
3 故障诊断实例
为了证实所提出的CEEMDAN-TFPF降噪方法的有效性,采用实测的双级齿轮传动减速齿轮箱来进行实验验证。首先测取齿轮箱正常运行时的振动加速度数据,再对第二级传动的小齿轮上作模拟点蚀破坏处理,再测取点蚀故障工况的振动数据。
加速度幅值实验采用的齿轮箱尺寸参数如表3所示,其中点蚀齿轮为第二级传动中的小齿轮,转动频率为6 Hz,啮合频率为97 Hz。数据采样频率为8 192 Hz,采用B&K数采仪采集了齿轮箱轴承座处的振动信号。
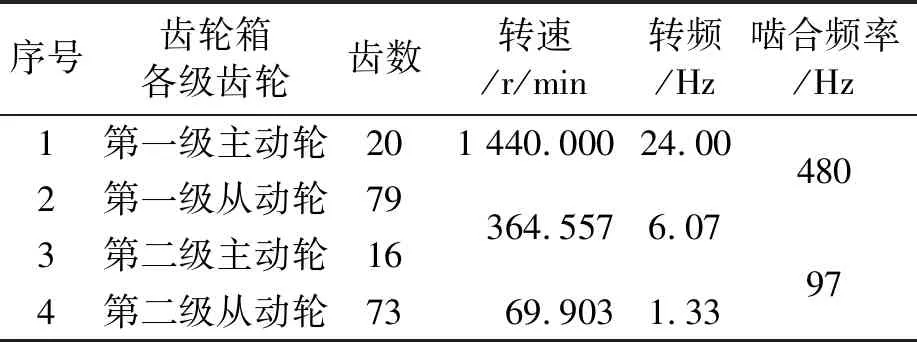
表3 齿轮箱传动参数
将测试信号利用CEEMDAN分解得到IMF结果,然后计算出各自的自相关函数及其方差值。将IMFs分为3类,分别进行不同窗长的TFPF降噪处理,降噪后结果如图8所示。最后将降噪后的分量和直接保留的分量一同重构,得到降噪后的信号如图9所示。

图8 各阶IMF处理后结果
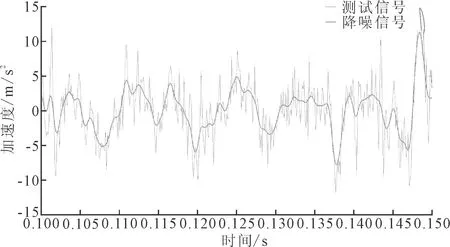
图9 联合降噪结果
联合降噪方法与传统TFPF方法结果如图10所示。联合降噪方法能够适用于信噪比低的测试信号,其降噪性能可靠,能够从含有噪声的测试信号中将有效信号成分恢复出来,且幅值不发生太大衰减,解决了传统TFPF方法的窗长限制,能够在信号保真和噪声抑制两个方面达到一个较好的平衡,降噪后信号信噪比提高,均方根误差减小,结果如表4和表5所示。

表4 正常工况降噪效果

表5 点蚀故障信号降噪效果
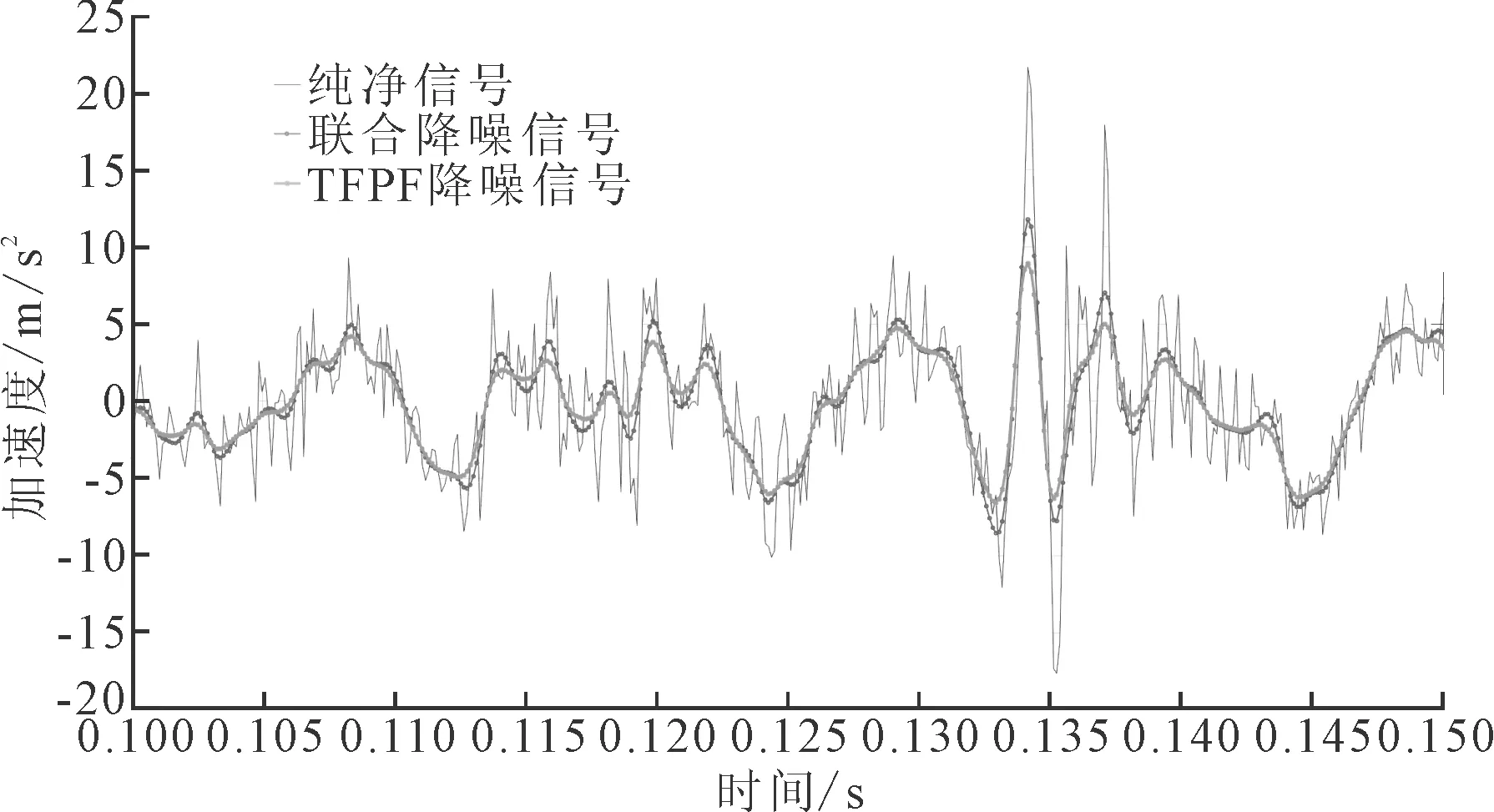
图10 与传统方法降噪结果时域对比
分别对正常工况和点蚀故障时的振动测试信号进行降噪处理并进行频谱分析。当齿轮箱内啮合的齿轮发生点蚀故障时,局部啮合刚度会发生周期变化,啮合频率受到调制,在频谱中会出现中心频率为啮合频率,间隔为故障齿轮转动频率的边频带,本次实验中,第二级传动的啮合频率为97 Hz,小齿轮的转动频率为6 Hz。
正常工况齿轮测试信号降噪后频谱如图11所示,发生点蚀故障后测试信号降噪后频谱如图12所示。采用联合降噪方法对振动信号处理,信号的信噪比有了较大提高,均方根误差也相应减少,结果表明联合降噪方法能够适用于齿轮振动信号的降噪处理。通过对比可以看出,点蚀故障发生后,降噪后的频谱中出现频率为96 Hz的峰值,其两侧存在以6 Hz为间隔的边频带,可以判断出是点蚀故障。结果表明联合降噪方法可以适用于复杂工况下的齿轮振动信号降噪。
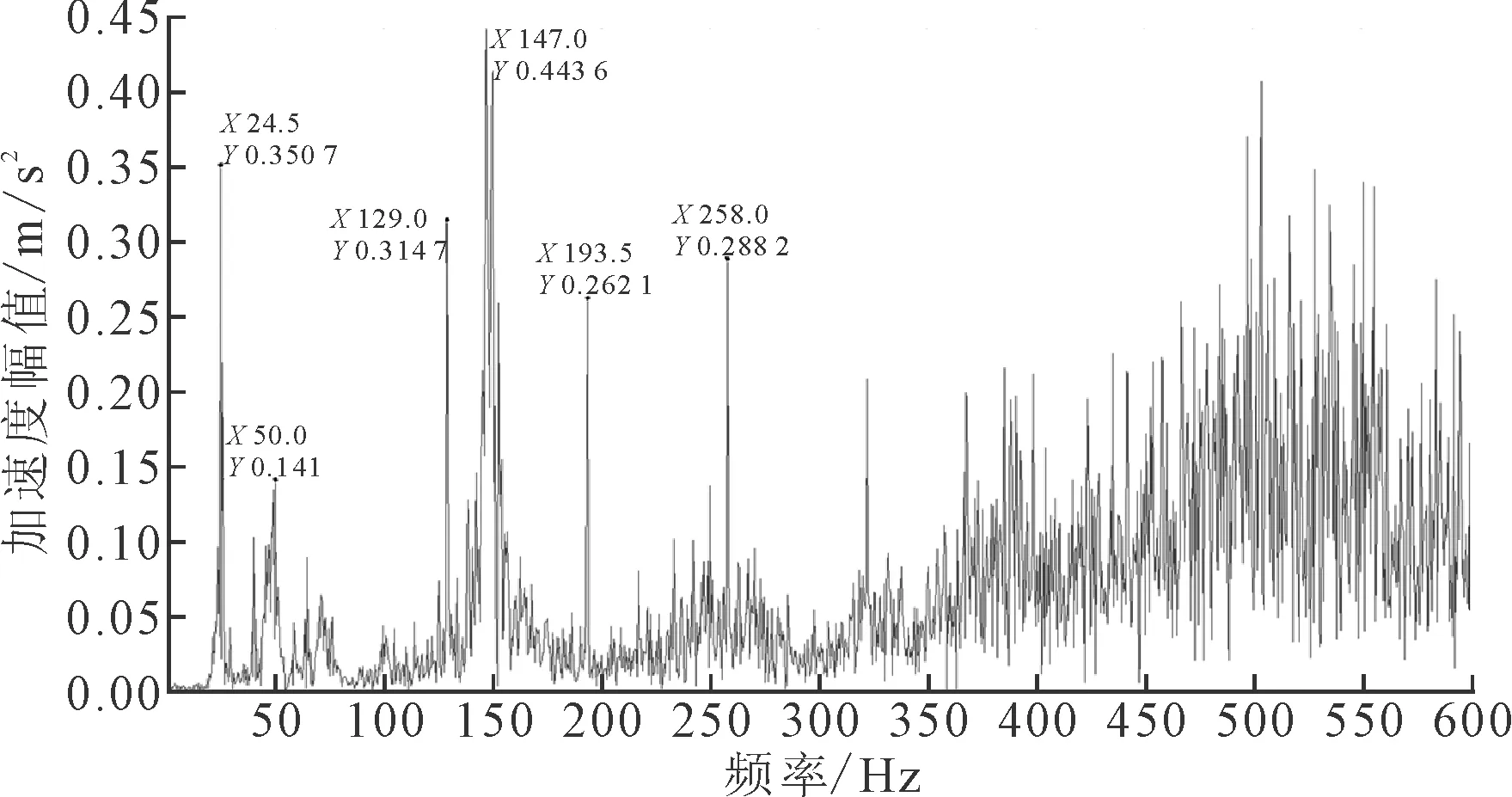
图11 正常工况频谱
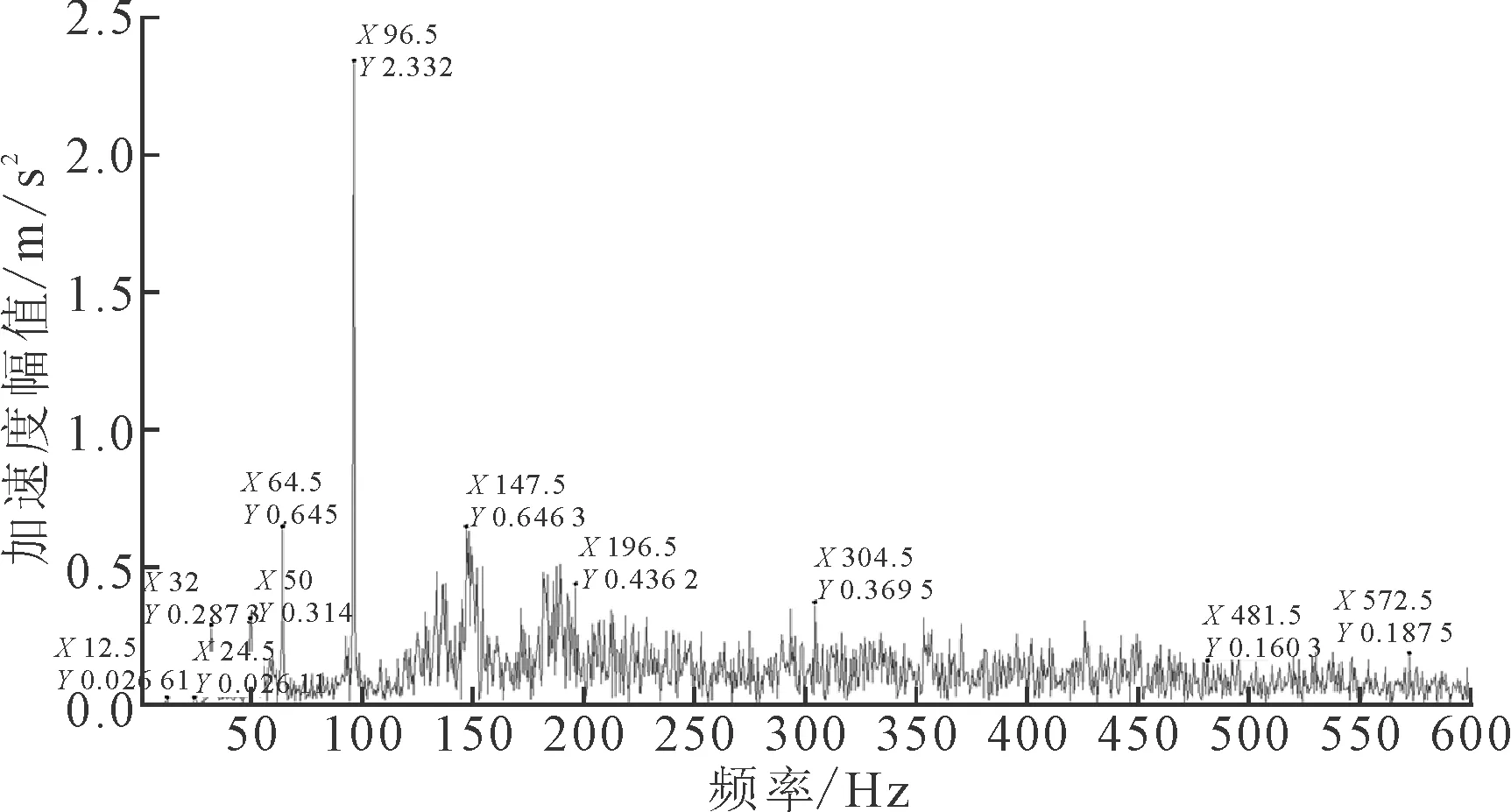
图12 点蚀故障频谱
4 结论
笔者提出了一种新的CEEMDAN-TFPF联合降噪方法,可适用于复杂工况下齿轮箱振动信号的降噪,其效果明显优于传统定窗长TFPF方法。利用仿真信号和实验测试信号验证了算法的可行性和可靠性。

