白噪声激励下螺旋桨模态参数识别方法研究
王子轩,丁国平,李 明
(武汉理工大学 机电工程学院,湖北 武汉 430070)
船舶振动不仅会影响船上人员的舒适性、危害人体健康,也会引起船舶局部结构疲劳损伤和设备的损坏,危害航行安全。在船舶上出现的有害振动中,大多数都是由螺旋桨振动所引起的[1-3]。对于处于水下的螺旋桨结构而言,其所受载荷无法测得,故可用运行模态参数识别方法来获取其运行模态参数。同时由于传感器的安装、排线等约束,用于振动测量的加速度计十分受限,因此给其运行模态测试带来很大困难。FBG传感器的兴起,提供了轻量、串联复用、抗干扰、可以水下监测结构动应变响应的测试途径,非常适合于水下螺旋桨的运行模态参数识别[4]。
运行模态分析是以准确获取结构模态参数为目标,为结构的设计和修改提供依据,能够有效解决结构的振动和噪声问题。国内外学者对运行模态参数识别方法做了大量研究,研究了识别方法在大型结构中的应用[5-7]、识别方法的计算效率[8]和识别精度问题[9-10]、在不同载荷形式下识别方法的普适性[11]问题等。目前,FBG传感器主要应用于结构的应变测量、损伤识别、载荷识别等方面,但将其应用于结构模态参数识别的研究却很少;目前对结构的运行模态参数识别问题大多集中在对大型静态结构的识别上,对于螺旋桨这种处于水下的结构较少。因此笔者以螺旋桨为研究对象,结合FBG传感器的独特优势,对其模态参数识别进行了相关研究。
1 白噪声激励下螺旋桨模态参数识别理论
基于协方差驱动的随机子空间(covariance-driven stochastic subspace ientification,COV-SSI)方法是基于输出协方差矩阵和状态矩阵的性质,对输出数据协方差矩阵作奇异值分解,以得到系统矩阵。
(1)构建Hankel矩阵。矩阵定义如式(1)所示,式中Y0|2i-1∈R2li×j含有2i块行和j列,其中每一块行由l行组成,l为输出通道的个数;R为实数集集合。可将矩阵Y0|2i-1分为过去和将来两个部分,分别用下标p和f表示过去和将来。
(1)
式中:yi为i时刻所有测点的响应。
(2)构造托普利兹(Toeplitz)矩阵。定义能观矩阵Ta∈Rla×n和能控矩阵Ma∈R2n×la为:
Ta=[CCACA2…CAi-1]T
(2)
Ma=[Aa-1GAa-2G…G]
(3)
式中:C为系统输出矩阵;A为系统状态矩阵;包含了结构的状态信息,如频率、振型和阻尼等参数;G为状态输出协方差矩阵。
由式(2)可知:能观矩阵Ta的前l行即为输出矩阵C。
Toeplitz矩阵Oi为:
(4)
(5)
式中:Λi为相应输出之间的协方差。
由式(2)~式(4)可得:
Oi=TaMa
(6)
(3)Toeplitz矩阵SVD(singular value decomposition)分解。将Toeplitz矩阵进行奇异值分解可得:
(7)
式中:U为左奇异矩阵;V为右奇异矩阵;S为奇异值组成的对角矩阵;U1、S1和V1分别为主分量的左奇异值向量、奇异值矩阵和右奇异值向量;U2、S2、U2分别为噪声分量的左奇异值向量、奇异值矩阵和右奇异值向量;U1∈Rli×N,S1∈RN×N,V1∈Rj×N;N为系数阶数。
比较式(6)和式(7)可得:
(8)
由式(2)、式(3)和式(6)可得:
Oi+1=TaAMa
(9)
将式(8)代入式(9)可得:
(10)
式中:(*)+为伪逆运算。
(4)系统模态参数计算。对矩阵A进行特征值分解,可以得到特征值矩阵Z和相应的特征向量Ψ满足:
AΨ=ΨZ
(11)
其中:
Z=diag(z1,z2,…,z2n1)
Ψ=(ψ1ψ2…ψ2n1)
n1=N/2
(12)
(13)

则结构模态参数的阻尼自然频率ωi和模态阻尼比ξi的表达式如下:
(14)
系统模态振型矩阵为:
Φ=CΨ
(15)
2 螺旋桨模态仿真分析
在进行螺旋桨试验前,需要对螺旋桨进行模态仿真分析以获得其模态节点位置,为试验中FBG传感器测点布置提供依据;同时,获得的各阶模态参数可作为试验识别结果的参照。仿真在ANSYS Workbench中的Modal模块中进行,本次螺旋桨结构的模态仿真基本流程如下:
(1)建立螺旋桨模型及设置材料属性。首先在UG中建立如图1所示的单叶螺旋桨三维模型,然后在ANSYS Workbench的项目分析流程图中创建模态分析项目,用于对单叶螺旋桨进行模态分析。最后将单叶螺旋桨的三维模型导入到ANSYS Workbench中,并在工程数据模块中设置单叶螺旋桨的材料属性。文中使用的单叶螺旋桨弹性模量E=6.9e10 Pa,泊松比为0.33,密度为2 700 kg/m3,它的主要几何参数如表1所示。

表1 单叶螺旋桨的主要几何参数

图1 单叶螺旋桨三维模型
(2)网格划分。网格划分是有限元分析的关键步骤,网格划分过稀会造成求解不精确,过密会造成求解时间漫长,且容易中断。对Details of Mesh模块中的相关参数进行设置,将Relevance设置为80,Relevance Center设置为Medium,Span Angle Center设置为Medium,其余默认;最后在Mesh模块中对单叶螺旋桨模型进行网格划分,划分好的单叶螺旋桨网格模型如图2所示。
图2 单叶螺旋桨的网格模型
(3)施加约束及模态求解。对螺旋桨浆毂的两个端面施加如图3所示的固定约束。设置最大模态提取阶数为10,其余默认;最后对单叶螺旋桨模型进行模态求解,其中单叶螺旋桨的前3阶固有频率分别为50.89 Hz,65.98 Hz, 148.59 Hz。前3阶阻尼比分别为0.056 4,0.050 1,0.031 1。前3阶应变模态振型如图4~图6所示。
图3 单叶螺旋桨约束图
图4 一阶应变模态振型

图5 二阶应变模态振型

图6 三阶应变模态振型
3 螺旋桨模态参数识别试验研究
3.1 螺旋桨激振测试系统及试验
螺旋桨结构所受到的白噪声激励主要来源于海浪等环境因素,但受到试验条件限制,无法满足螺旋桨在水下受到白噪声激励,现对试验条件进行简化,采用激振器对单叶螺旋桨进行白噪声激励。在本试验中的金属螺旋桨模型与仿真中的三维模型一致,采用1∶1的比例加工,材料选用6061-T6型铝合金。
针对螺旋桨结构的不规则性,为查看不同方向的模态参数识别效果,在金属螺旋桨上的7个测点处各布置2个FBG传感器,分别沿着导边和垂直于导边两个方向布置。定义沿着导边方向为0°方向,垂直于导边方向为90°方向。图7为粘贴好FBG传感器的螺旋桨,为便于观察FBG传感器的位置分布情况,现采用记号笔将FBG传感器标出。

图7 螺旋桨光栅布点图
将FBG传感器粘贴在螺旋桨桨叶表面后,搭建螺旋桨激振试验平台。用G型夹将金属螺旋桨固定在试验平台上,使用解调仪以1 kHz的采样频率对FBG传感器进行解调采样。由于所使用的解调仪最多只能连接8个通道,因此试验分两次对FBG传感器进行解调采样,首先对0°方向的7个FBG传感器进行解调采样,然后在同样的试验条件下,对90°方向的7个FBG传感器进行解调采样。本次试验中激振器的激励方式为倾角激励,使用AB胶将力传感器固定到螺旋桨结构上,将力传感器与顶杆相连接,通过调节激振器底座方向使顶杆在激励点处与螺旋桨表面垂直。使用导线将力传感器与BK主机箱连接,通过BK主机箱采集螺旋桨所受激励信息。通过导线将BK主机箱、功率放大器以及激振器连接起来,通过电脑对输入信号进行控制,由BK主机箱发出的白噪声激励信号经功率放大器放大后传递到激振器,实现金属螺旋桨的激振。其试验原理如图8所示。

图8 螺旋桨激振试验原理图
3.2 试验结果分析
在试验中,由阻抗头获得的激振力信号的概率密度曲线如图9所示,同时可以得到螺旋桨上7个测点处的FBG传感器中心波长偏移量,现以其中一个0°方向的FBG传感器为例,根据波长与应变之间的转换关系,使用MATLAB将FBG传感器的中心波长偏移量转换为螺旋桨的应变响应值,获得如图10所示的应变时域曲线。
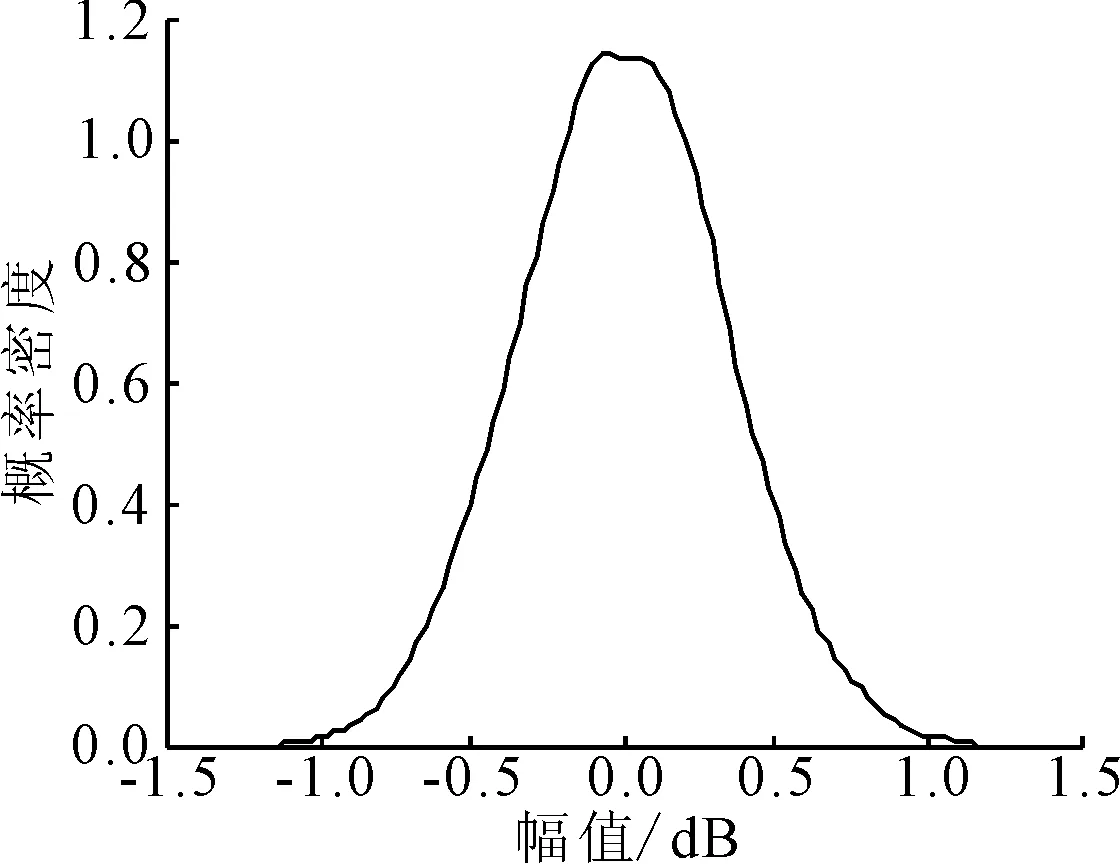
图9 激振力信号的概率密度曲线
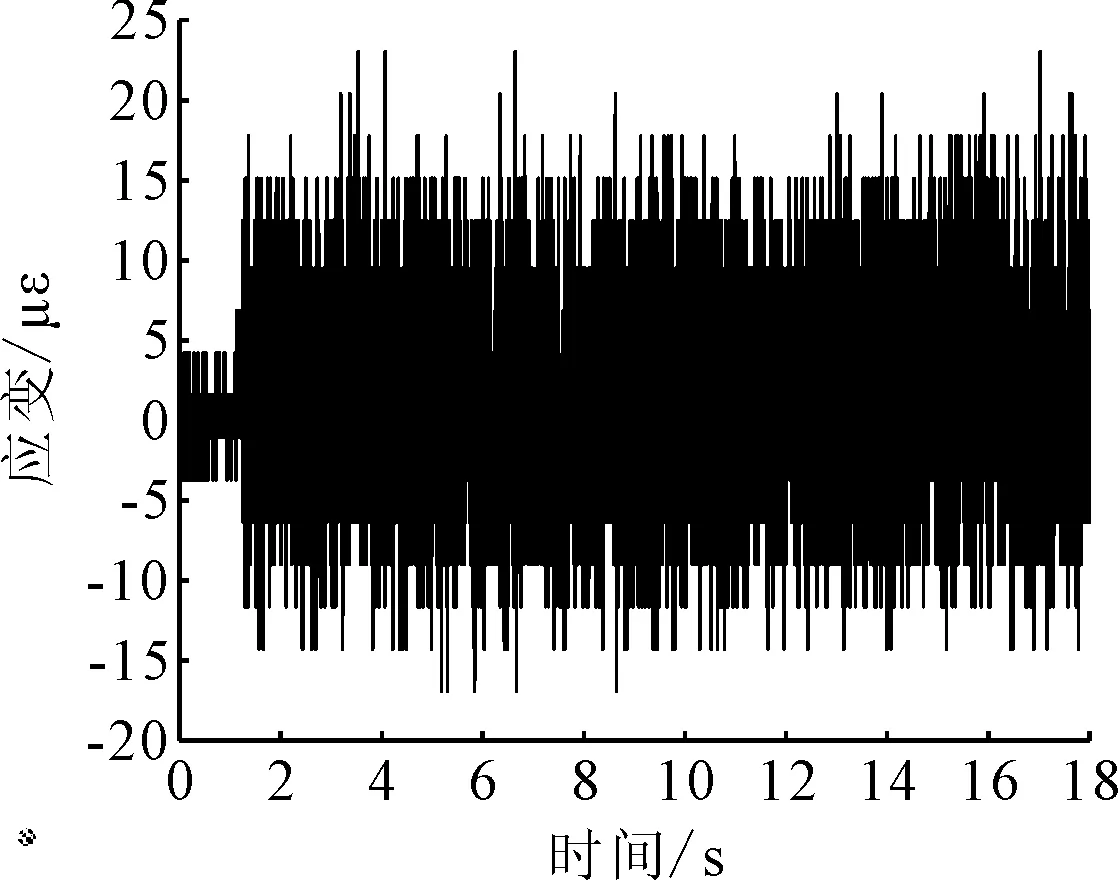
图10 FBG传感器应变时域曲线
从图9可知,激励信号的概率密度曲线符合正态分布,满足使用随机子空间SSI法时激励是白噪声的前提条件。接下来将各个测点的应变值作为输入代入SSI法进行模态参数识别,0°方向的FBG传感器在白噪声激励下的稳定图如图11所示,识别出的模态参数如表2所示,90°方向的FBG传感器在白噪声激励下的稳定图如图12所示,识别出的模态参数如表3所示。

表2 0°方向模态参数识别结果
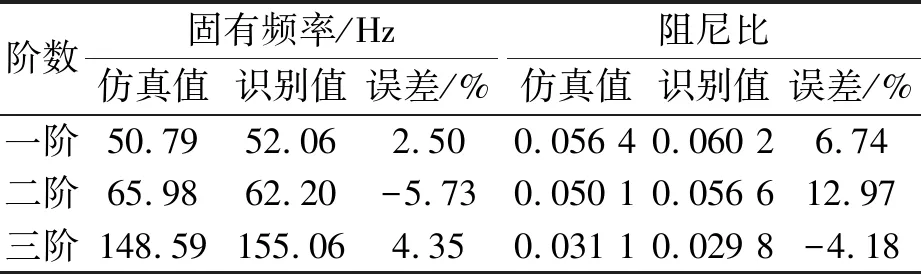
表3 90°方向模态参数识别结果

图11 0°方向白噪声激励下稳定图

图12 90°方向白噪声激励下稳定图
从图11和图12可知,在稳态图中绝大部分极点均落在自功率谱的峰值处,表明无论是0°方向还是90°方向SSI法都可以准确识别出单叶螺旋桨在白噪声激励下的模态参数。从表2和表3可知,无论是0°方向还是90°方向SSI法识别出的固有频率和阻尼比都与仿真值很接近,固有频率的最大误差不超过6%,阻尼比的最大误差不超过15%。
在振型方面,提取出模态仿真分析中与试验测点相对应点的应变模态振型值,并做最大系数归一化处理,0°方向仿真值和识别值如表4所示,90°方向仿真值和识别值如表5所示。
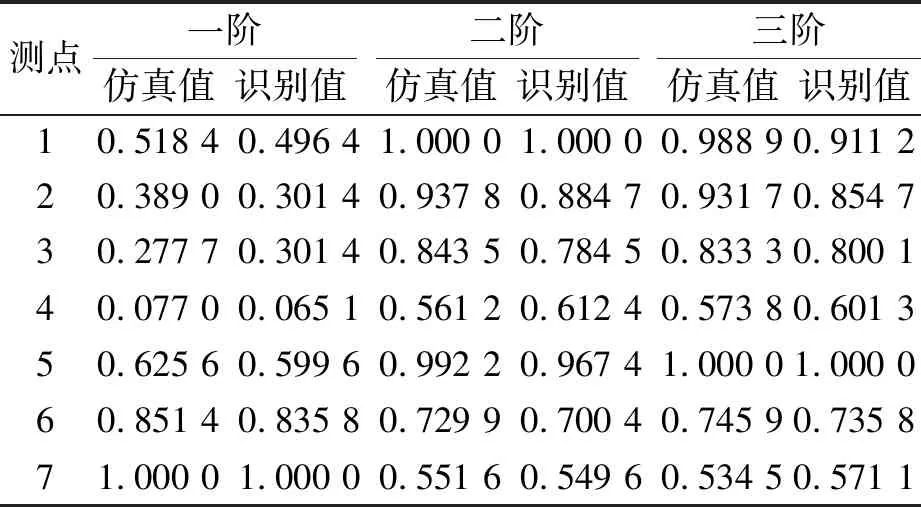
表4 0°方向应变振型系数
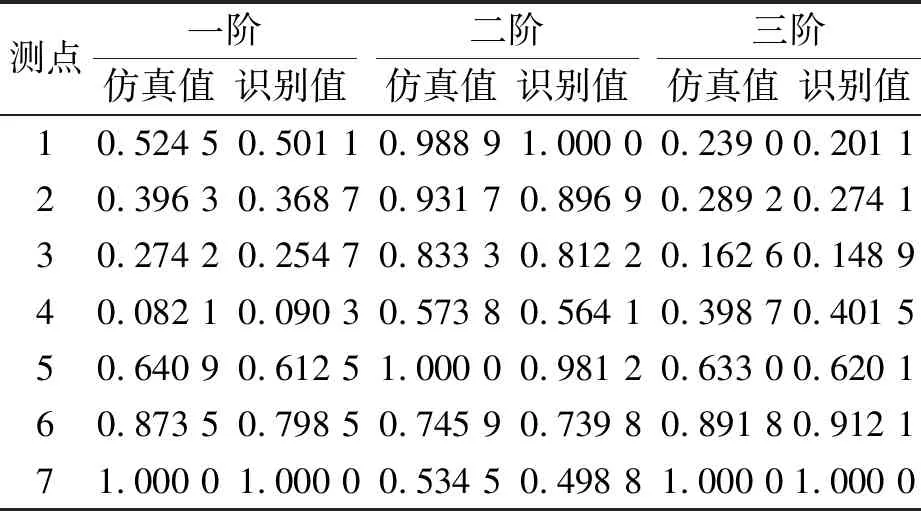
表5 90°方向应变振型系数
以仿真值作为基准,0°方向识别误差如图13示,90°方向识别误差如图14所示。
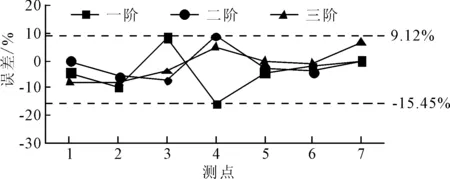
图13 0°方向识别误差图
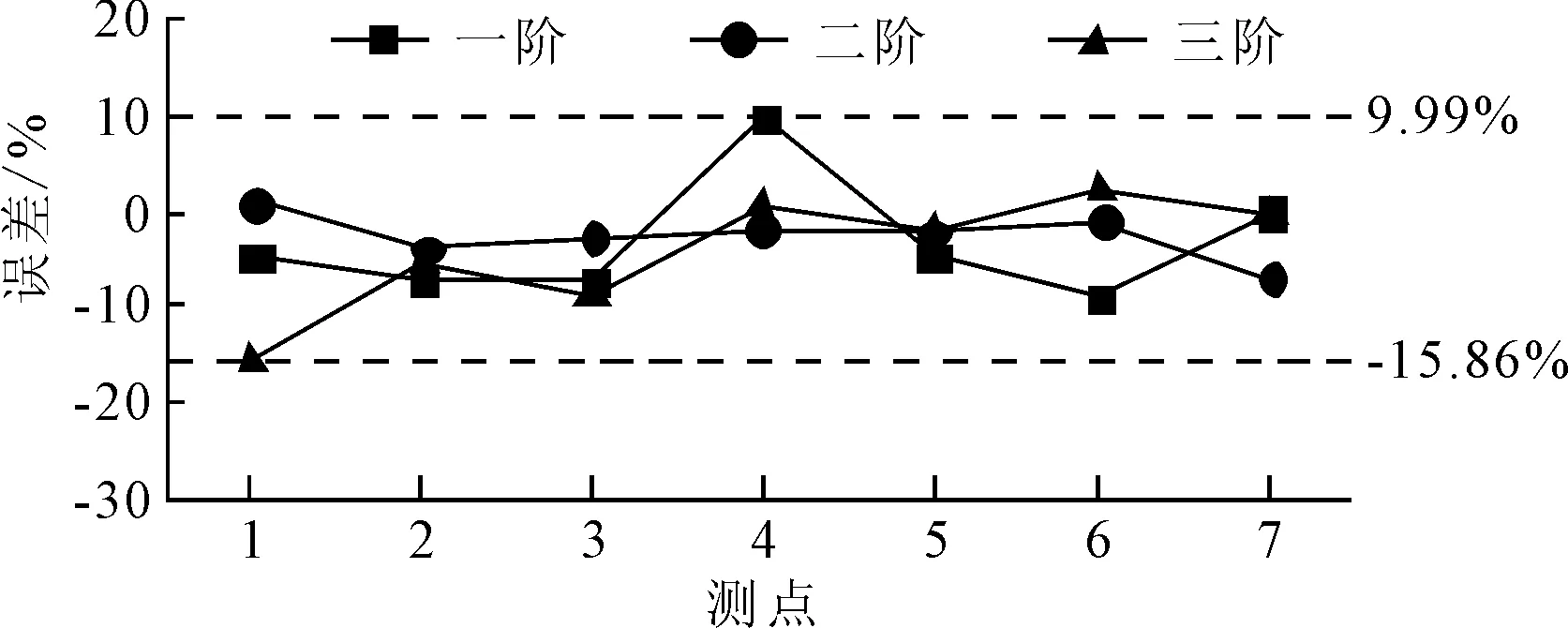
图14 90°方向识别误差图
从表4、表5、图13和图14可知,无论是0°方向还是90°方向,SSI法识别出的前三阶应变振型系数和仿真得到的应变振型系数都具有很好的一致性,其最大误差为15.86%。
4 结论
笔者以单叶螺旋桨为研究对象,利用SSI法并结合仿真分析实现了单叶螺旋桨在白噪声激励下的模态参数识别。在固有频率方面,0°方向上的最大误差为4.33%,90°方向上的最大误差为5.73%;在阻尼比方面,0°方向上的最大误差为14.17%,90°方向上的最大误差为12.97%;在应变振型系数方面,0°方向上的最大误差为15.45%,90°方向上的最大误差为15.86%,误差均在可接受范围内。表明用SSI法来识别螺旋桨在白噪声激励下的模态参数具有很好的准确性和可靠性。

