基于高品质因数波导型缩比例船形腔的多物理场耦合仿真研究

刘景源,裴士伦,张天爵,殷治国,汪 洋

(中国原子能科学研究院 核技术综合研究所,北京 102413)

高能强流质子加速器在核物理与粒子物理等前沿研究领域、大众健康和先进能源等国民经济领域,均有着十分广泛而重要的应用[1-2]。近年来,中国原子能科学研究院提出1套可产生2 GeV、6 MW连续波质子束的强流回旋加速器组合方案,其中包含100 MeV直边分离扇回旋加速器、800 MeV螺旋分离扇回旋加速器和2 GeV 连续波(CW)固定场交变梯度加速器(FFA),3台加速器的高频腔均工作在44.4 MHz,最终可实现加速器组合全流程连续束、等时性高效率加速和高平均质子束流功率输出[3]。在分圈式等时性加速器中,当束流加速到引出阶段,提高螺旋轨道圈的间距,加大留给引出装置的安装空间,可有效降低束流被引出装置阻挡,提高引出效率,实现单圈引出。在回旋式等时性加速器中,在运动方向上,束流的纵向聚焦力较弱,纵向空间电荷效应引起的流强阈值与束流圈能量增益的3次方呈正比[4-5],较横向空间电荷效应引起的流强阈值低很多。根据PSI实验室高功率质子加速器的长年运行调试经验,受空间电荷影响,束流流强与圈能量增益的3次方呈正比,该实验室590 MeV回旋加速器先后使用的矩形腔体或欧米伽腔体已较难满足更高的电磁储能需求[6-8],经过对矩形、欧米伽形和跑道形等多种形状的波导型高频腔进行系统研究,提出全流线形的船形高频腔设计方案[9]。高频腔径向变轨范围约2.8 m,加速电压可达到2 MV,谐振频率44.4 MHz、Q值高达90 000。

为掌握船形高频腔的加工工艺,采用ANSYS HFSS和ANSYS workbench设计工作在177.6 MHz的1∶4缩比例船形腔,开展腔体频率调谐的仿真研究工作和腔体的样机研制,同时利用现有的高频功率源开展相关高频功率实验研究。本文将采用稳态热分析和Fluent两种热仿真软件对该腔体样机进行多物理场耦合仿真计算,研究船形腔温度分布、结构变形和频率变化。

1 设计指标要求

该船形腔经过适当调整,可在不对腔体的高频性能造成任何影响的情况下,改造为一台引出电子束能量5～6 MeV、引出靶上平均流强16～20 mA、引出靶上功率90～100 kW的高能电子加速器,图1所示为加速器基本结构与原理示意图[10]。

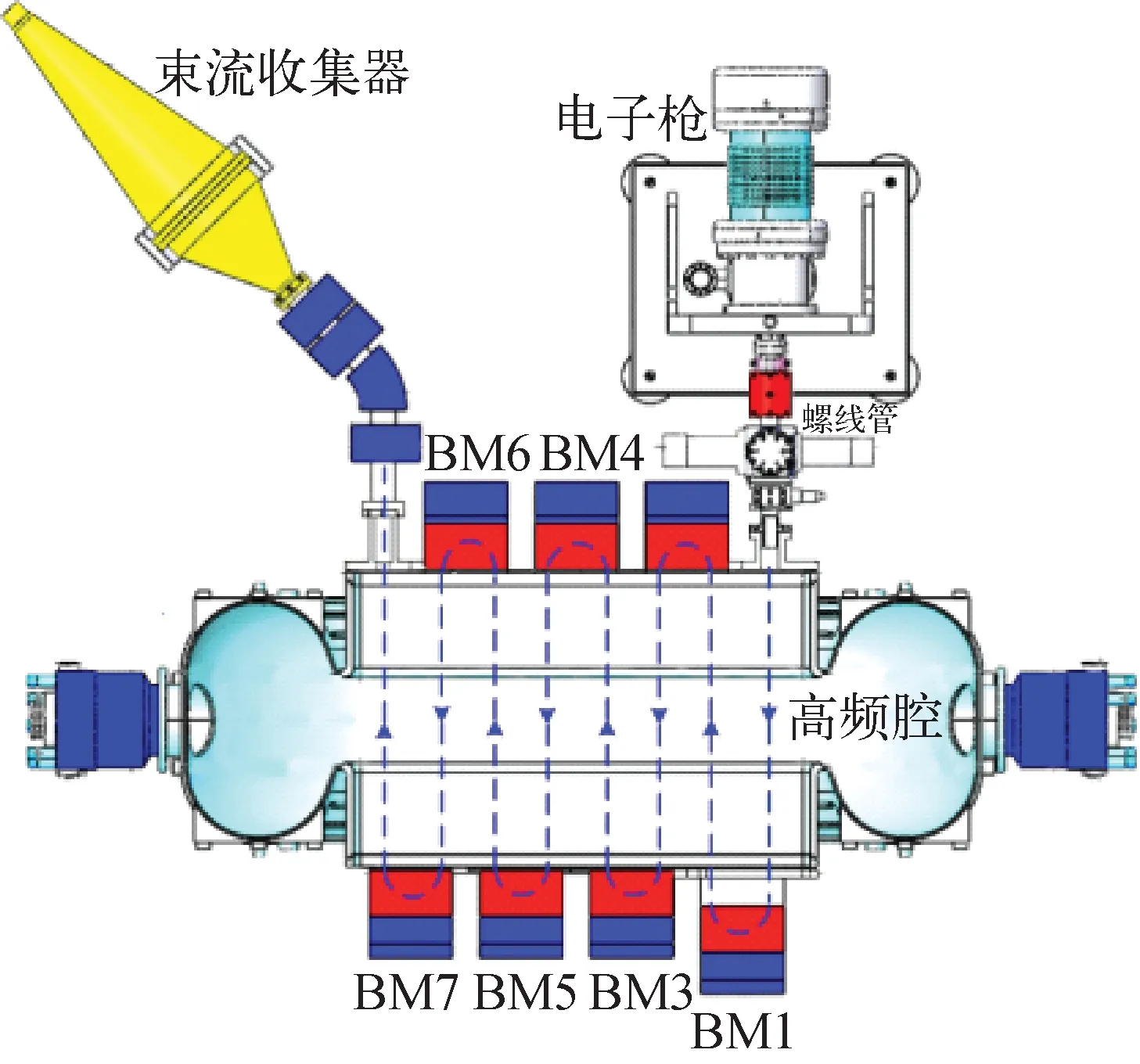
图1 高能电子加速器基本结构与原理示意图

综合考虑2 GeV CW FFA高频腔的性能指标和1∶4缩比例船形腔样机在电子回旋加速器工程应用中的要求,缩比例腔需满足以下要求:1) 缩比例腔体谐振频率调谐范围要求能达到±170 kHz左右;2) 高功率运行时,损耗在腔体上的RF热功率约为100 kW,冷却水若能将这部分热量全部带走,冷却水管出口相对35 ℃入口水温的温升要求<10 ℃;3) 在计入大气压力、电动缸拉力或压力、RF热功率、重力及各种位移约束等的情况下,机械结构变形导致的等效应力应尽可能低,以方便选用合适形态的无氧铜板材及不锈钢材。图2示出缩比例腔机械设计总装结构,该腔体主要由主腔体、支撑组件及调谐电动缸组件等组成,频率调谐采用电动缸上下拉压船形腔体复合板外壁的方法实现。

图2 缩比例腔机械设计总装结构

2 多物理场耦合仿真理论

常用的波导型高频腔有矩形波导型和圆柱形波导型,两者在电磁场分布和特性参数计算上类似[11]。2 GeV FFA中所使用的高频腔为矩形波导型,图3为高频腔的示意图,此种类型高频腔中的模式有两种,分别为TEmnp模和TMmnp模,m、n及p分别对应x、y及z方向上出现电磁场极大值的个数,a、b及d分别为腔体在x、y及z方向的长度。TEmnp模或TMmnp模的谐振频率可表示为:

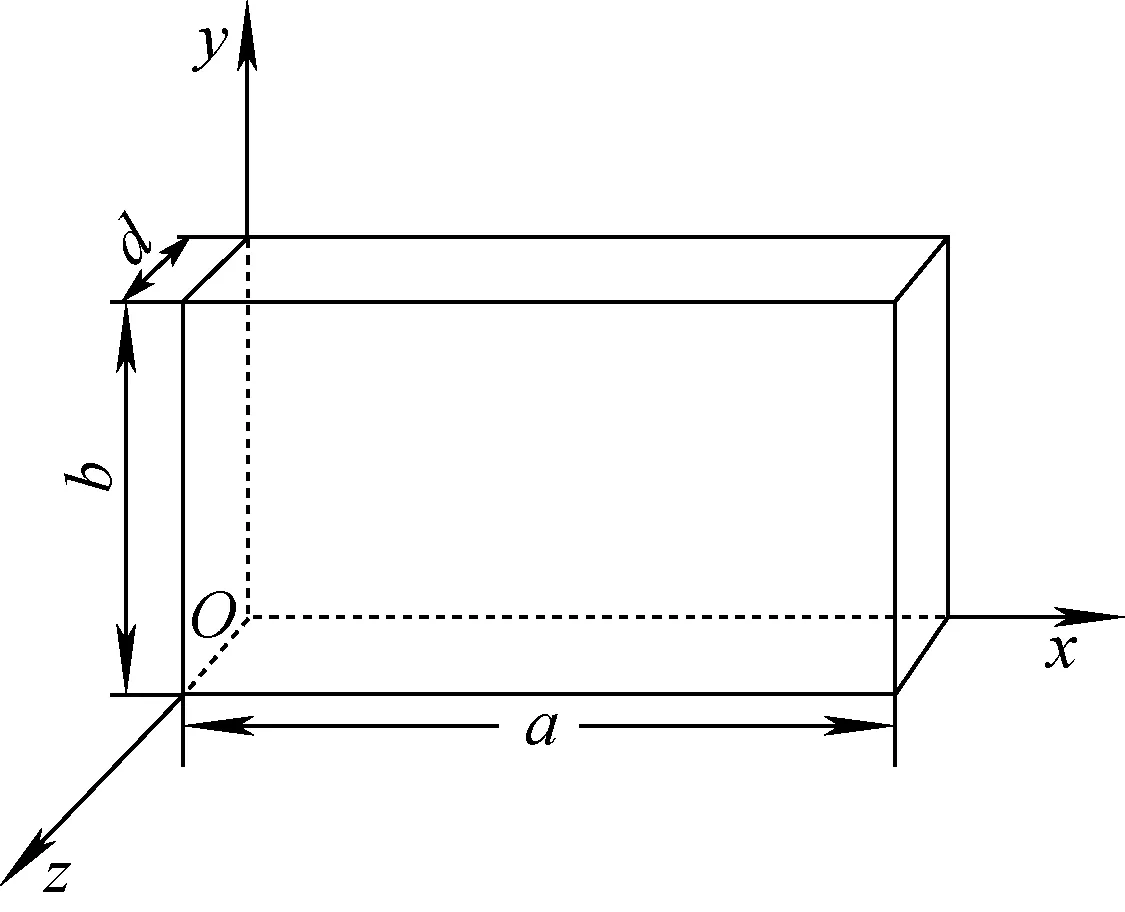
图3 矩形波导型高频腔示意图

(1)

若束流沿z轴穿过高频腔并获得加速,腔体需在其运动方向上提供加速电场。考虑到高频腔中用基模加速,则矩形波导型高频腔的工作模只能选TM110模,即a>b>d或b>a>d,图4示出TM110模的电磁场分布形式。为使束流能无阻碍穿过高频腔,在腔上沿x轴(即圆形加速器的半径方向)开设了长条形束流通道。腔内电场Ez沿x轴和y轴均呈半正弦分布,在靠近腔体沿x轴两端的电场Ez太低,不能用于加速,由此束流通道在沿x轴方向上的长度要小于a,既要满足设计需求又要小于a。由式(1)可知,矩形波导型高频腔TM110模的频率与d无关,因此该类型的高频腔可设计成长窄型(即d较小),这样非常有利于增加加速器在粒子束运动方向上安装空间,实际高频腔与图4在形状上会有所差异,需借助3维计算机软件来对其进行计算和优化[9]。

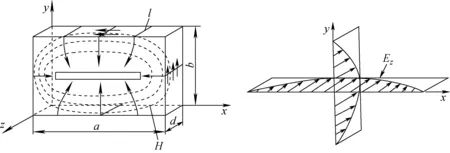
图4 矩形波导型高频腔中TM110模场分布

矩形波导型高频腔在高功率运行时,在腔体内表面会产生大量热损耗,这些热量主要通过热传导和热对流被带走。根据运行经验,冷却水出口温度相对入口的温升应≤10 ℃,船形腔冷水流速一般<3 m/s。流速过高容易引起机械震动,流速过低无法及时带走腔体产生的热量,经综合考虑后缩比例腔采用2 m/s[12-13]。整个腔体本体外部布置TU1水管,要求冷却水能带走的热耗散功率约为100 kW,计算分析按照平均35 ℃水的对流换热系数来计算。选择10 mm×10 mm、壁厚1 mm的TU1水冷管进行计算。

传热仿真计算中,首先需要确定水冷管的流动状态,流动状态根据式(2)、(3)计算得到Re。

(2)

(3)

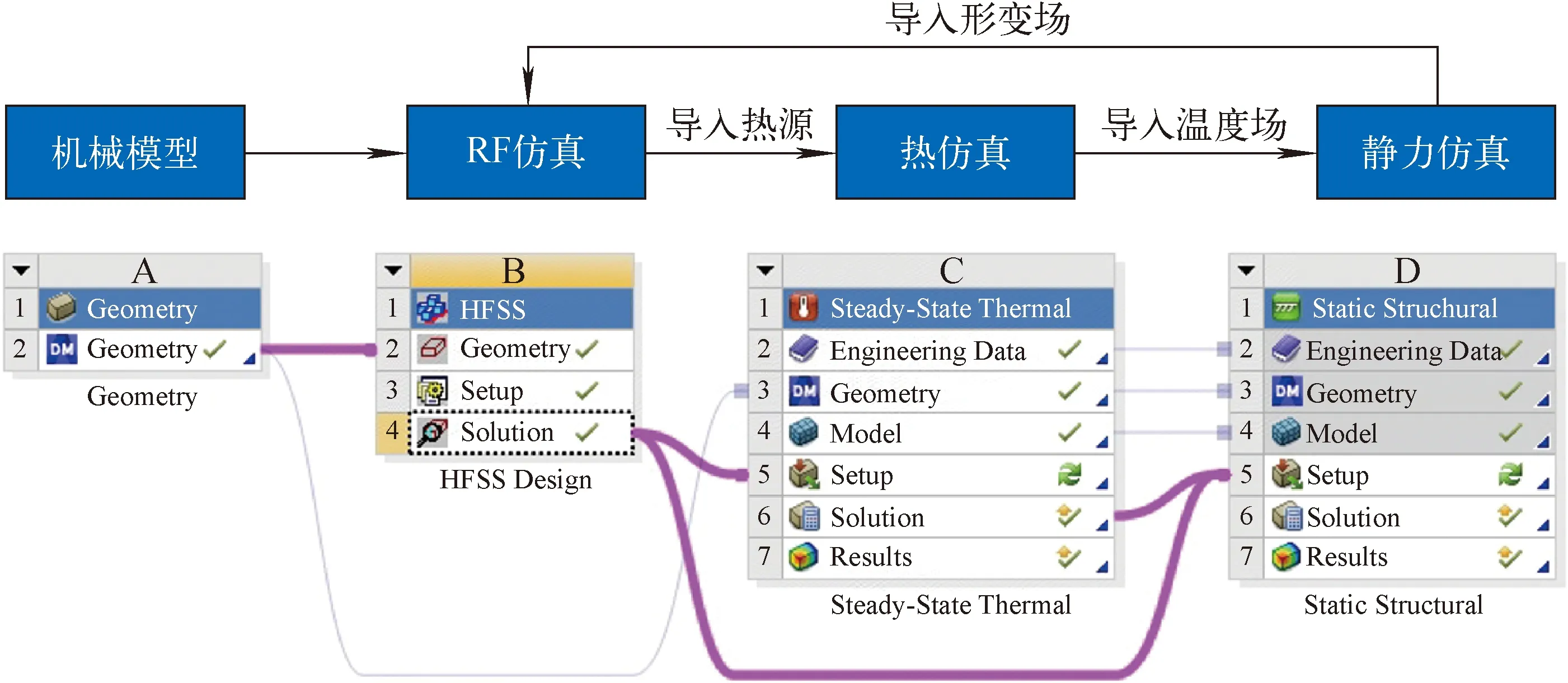
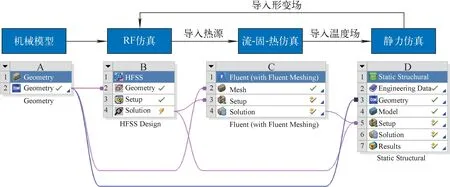
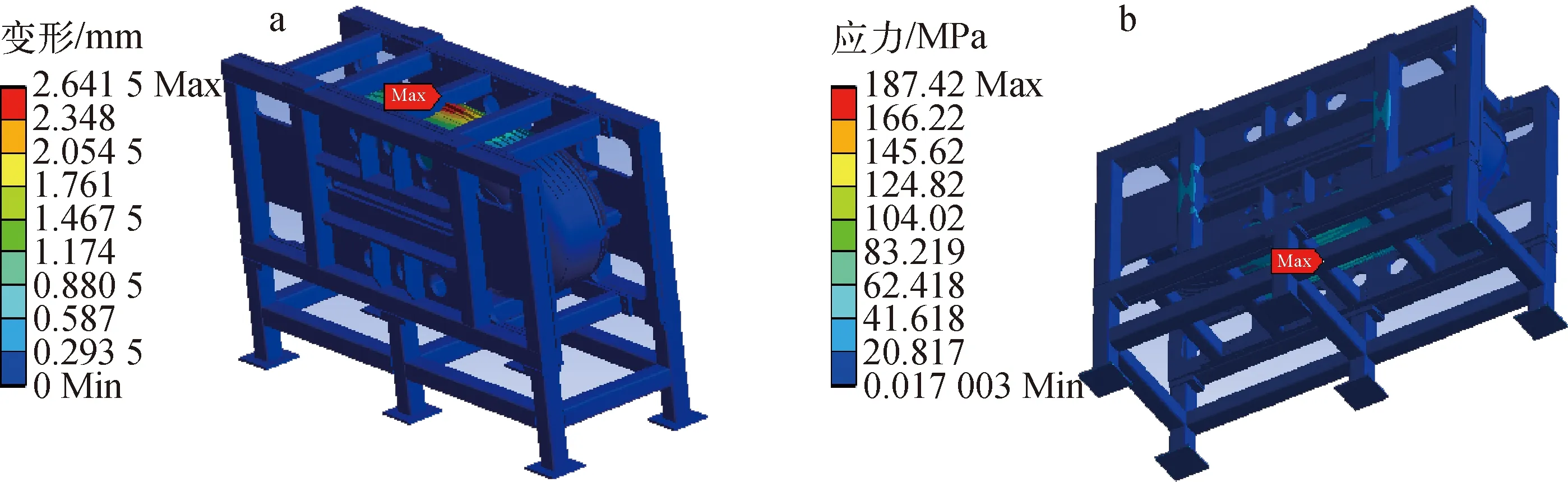
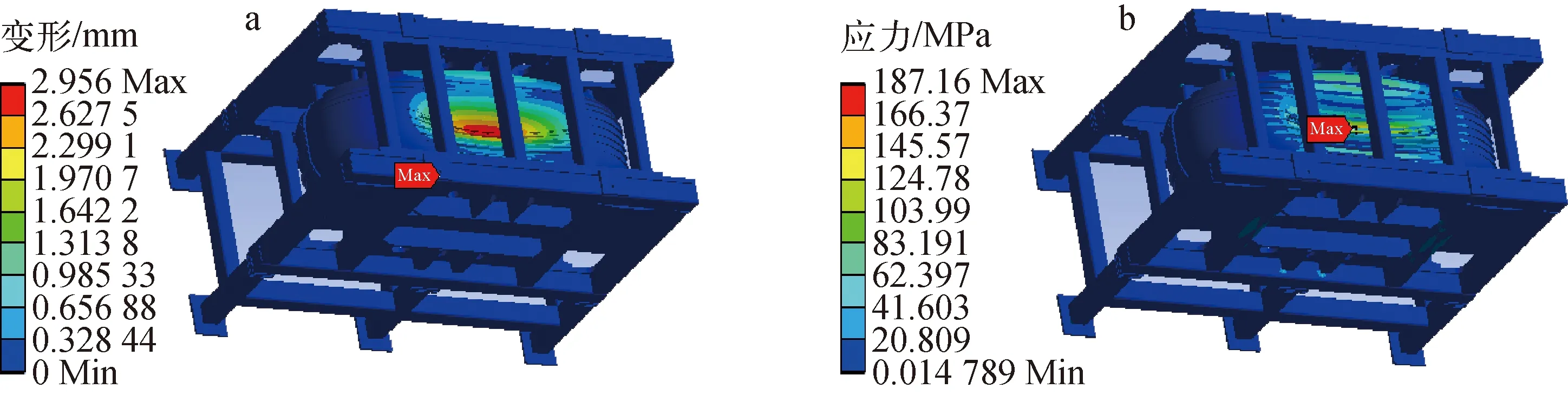
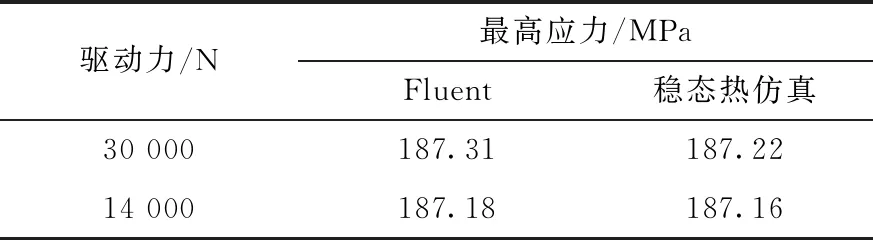
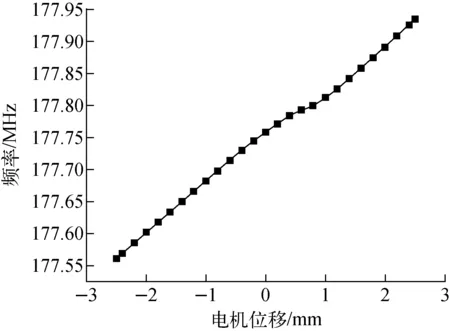
式中:S为非圆断面的过流截面面积;L为过流截面上流体与水冷管壁接触的周长;v为介质流速;ρ为介质密度;η为动力黏度系数。物性参数列于表1,可计算出Re=19 875,水冷管处于湍流状态。由于104

表1 35 ℃水的物性参数

(4)

式中:Prw为普朗特数;κw为冷却介质的导热率。式(4)的使用条件是:当流体被加热时n=0.4,而流体被冷却时n=0.3;管长与直径比≥60;壁面温度和冷却水主流温度之差在20～30 ℃[14],对于本文计算腔体,属于流体被加热过程,n取0.4。计算得对流换热系数约为8 100 W/(m2·K)。

通常矩形波导型高频腔采用铝或铜等金属板加工而成,腔体由薄壁金属板焊接成型[12]。腔体周围需设计固定结构和支撑结构,防止矩形波导型高频腔在受到重力、大气压力、调谐过程中产生的拉和压力产生变形。2 GeV FFA中所使用的高频腔采用Y/2态TU1母材板电子束焊加工。Y/2态母材的抗拉强度、屈服强度和伸长率分别约为220 MPa、103 MPa和65%[15-16];Y/2态电子束焊拉伸试样的断裂均位于焊缝处,抗拉强度分别约为235 MPa和225 MPa。其一次和二次许用应力限值分别为68.7 MPa和206 MPa。

3 多物理场耦合仿真

图5示出了在ANSYS Workbench中开展“RF-热-结构-RF”全自洽闭环多物理场有限元分析的具体流程,使用Steady-State Thermal模块开展固热分析。导入到Geometry中的Solidworks机械模型包含有两种类型的实体部件:金属和非金属实体部件。在HFSS中,与RF场相关的非金属实体和金属实体与RF场计算相关,只计算这些区域以使整个模拟计算可顺利进行并效率更高。为了使计算分析更接近实际情况,RF计算完成后需调节腔体内部储能到4 J,由此可使高频功率损耗达到设计要求的100 kW。在固热分析中,RF损耗将其设置为热负载。在这种情况下,将对流系数和壁面冷却水温度作为边界条件,计算得到腔体温度分布。在静态结构分析中,将腔体温度分布结果作为负载导入静态结构分析模块,设置重力、大气压力、固定支撑等约束,计算得到整个腔体机械模型的变形及应力分布。为了评估结构变形对RF场的影响,选择对应的实体设置并设置结构变形反馈功能。将计算得到的变形反馈给HFSS,然后再评估机械变形对腔体RF性能的影响。多次迭代上述过程,可获得稳定的计算结果。但在大多数情况下,一次或两次迭代即可。

图5 基于Steady-State Thermal模块的船形腔多物理场仿真流程图

固热分析的方法在设置边界条件时,对水冷管各处做了温度分布均匀、对流换热系数相等的假设。使用Fluent开展流固热分析时,通过设置运动参数、物性参数和计算方程,仿真过程中逐步计算得到水冷管温度,这样的结果更符合实际情况。图6示出了基于Fluent的多物理场仿真分析流程,使用流体仿真模块Fluent模块代替Steady-State Thermal模块,该方法较固热分析略微复杂,对模型的要求较高,在不影响整体分析结果的基础上对导入的模型进行一定的调整,修补不适用于Fluent的模型缺陷。综合考虑计算机性能和计算时间等条件,在进行网格划分和流体传热仿真时,不考虑船形腔的支撑组件,将HFSS计算得到的腔体内壁功率设置为Fluent的热负载。设置冷却水进口流速和温度,根据式(3)得到Re,求解模型采用k-ε模型。

图6 基于Fluent的船形腔多物理场仿真流程图

4 计算结果及讨论

表2列出HFSS仿真计算的腔体功率损耗分布,在谐振频率177.848 MHz下腔体无载Q值约为44 157.7。

表2 功率损耗分布

4.1 温度分布特性

图7分别示出稳态热分析和Fluent仿真的腔体温度分布,稳态热分析显示腔体最高温度为77 ℃,Fluent仿真计算得到腔体最高温度为82.6 ℃。两种方法均显示腔体最高温度分布出现在鼻锥两端根部区域。对比可发现,稳态热分析结果中腔体温度沿y-z平面对称分布,而Fluent仿真计算结果显示,腔体出口附近温度比进口附近高约4.7 ℃。腔体热量可被冷却水带走,且冷却水进出口温升小于10 ℃,满足设计指标要求。

a——稳态热仿真;b——Fluent仿真

在Fluent计算结果中,腔体总流量为Q=6.713 L/s,进出口平均温升为ΔT=3.6 ℃,计算得到腔体总功率为100.89 kW。在Fluent的计算结果中提取水冷管壁面温度Tw、热流密度q及管内主流温度Tf,水冷管壁面温度根据牛顿冷却公式(式(5))计算得到腔体管道对流换热系数为7 532～8 573 W/(m2·K),与式(2)～(4)计算的理论值基本一致。

q=h(Tw-Tf)

(5)

4.2 腔体变形及频率调节

为了获得±170 kHz的频率调谐范围,分别在船形腔上部和下部各设置3个电动缸。利用电动缸对船形腔体铜壁施加拉力或压力后,会使其内部真空部分的体积发生变化。因为拉力或压力均施加在船形腔内RF磁场较强、电场较弱的区域附近,所以拉腔体会使其频率降低、压腔体会使其频率升高。图8、9分别示出了利用调谐装置将船形腔频率调变-164 kHz和+176 kHz时得到的机械变形及应力分布,最高应力出现在电动缸复合板位置。当腔体频率调变-164 kHz时,主腔体最大变形为2.64 mm,最高应力为187.22 MPa(二次应力),此时船形腔上部和下部的电动缸对应的总拉力均为30 000 N。当船形腔频率调变+176 kHz时,主腔体最大变形为2.96 mm,最高应力为187.16 MPa(二次应力),此时船形腔上部和下部电动缸对应的总压力均为14 000 N。最高应力低于TU1二次应力3[P]=R态204 MPa。

a——机械变形分布;b——应力分布

a——机械变形分布;b——应力分布

在将船形腔谐振频率调高或调低几乎相同的量时,总压力仅约为总拉力的1/2,这是因为船形腔正常工作时内部为真空状态,主腔体铜壁外表面受到1个大气压的压力作用。无论是利用电动缸拉还是压腔体,所造成的变形都会在拉力或压力施加点附近造成较高的应力,实际加工腔体时的焊缝应尽最大可能远离这些区域。

图10、11分别示出将电动缸设置为拉力30 000 N和压力14 000 N,基于Fluent的多物理场有限元仿真得到的温度分布腔体机械变形及应力分布,最大变形和最高应力都分布在上下电动缸复合板区域。电动缸总拉力为30 000 N时,船形腔主腔体最大形变为2.61 mm,最高应力为187.31 MPa。电动缸总压力为14 000 N时,船形腔主腔体最大形变为2.50 mm,最高应力为187.18 MPa,腔体调谐范围为329 kHz。

a——机械变形分布;b——应力分布

对比图8和图11可得:相同参数下,两种仿真方式得到的腔体频率变化范围相差11 kHz;基于Fluent的多物理场仿真计算得到的变形小于基于稳态热分析的结果;前者计算得到的腔体受到的最大应力大于后者的结果。表3、4分别给出最大变形和最高应力。造成这些差异的原因除了计算误差和温度分布条件不一致外,还有静态结构分析约束条件的差异。受计算机性能限制,基于Fluent的仿真流程需要减少对支撑组件的静力学计算,只能以腔体固定板端面作为固定面。而约束条件的改变,造成原本可以被腔体、固定板和支撑组件共同分摊的应力,只能由腔体来承担。

表3 腔体最大变形

表4 腔体最高应力

a——机械变形分布;b——应力分布

5 缩比例船形腔冷测

图12示出腔体在15 ℃的环境温度下,通过分子泵将腔体真空度提高到8.1×10-8mbar,电机驱动位置从-2.5 mm变化到2.5 mm测得的腔体频率变化曲线。腔体频率变化范围为177.561～177.935 MHz,腔体加工满足设计需求。在大气状态下,利用2个耦合度极小的小耦合环,通过S21扫频曲线对无载品质因数进行测量,测得Qs≈42 314,约为模拟计算值44 157.7的95.8%。

图12 腔体冷测频率曲线

6 结论

本文利用ANSYS workbench开展了基于稳态和Fluent热分析的船形腔多物理耦合仿真计算。结果表明,腔体最高温度分布在鼻锥两端根部区域,主腔体表面温度分布均匀,水冷管布置合理,可带走腔体耗散能量。两种热分析结果对比显示,Fluent仿真结果更接近实际情况。静态结构分析表明应力主要集中在上下电动缸复合板区域,最高应力低于TU1二次应力的许用要求。基于稳态热分析的多物理耦合仿真和实际冷测均显示腔体频率变化范围满足设计需求。受计算机算力影响,基于Fluent的多物理耦合仿真对模型优化,无法完全模拟腔体的受力约束情况,导致与稳态热分析相比,腔体频率变化范围的结果相差11 kHz。