超临界二氧化碳压缩机性能不确定性量化研究
马 灿,代 路,吕伟剑,张克龙,*
(1.热能动力技术重点实验室,湖北 武汉 430205;2.武汉第二船舶设计研究所,湖北 武汉 430205)
超临界二氧化碳(S-CO2)循环在核电领域具有良好的应用前景,近年来得到了越来越多的研究[1-2]。压缩机是S-CO2动力循环中的关键设备,其性能对动力循环特性有较大的影响。在二氧化碳反应堆一回路中,压缩机是工质循环的关键设备,直接决定了一回路系统的耗功,在二氧化碳二回路系统中,压缩机是工质压缩的关键设备,对二回路系统的热功转换效率有着较大影响。
由于加工制造误差和系统状态波动,S-CO2压缩机设计和运行参数存在不可避免的随机波动,如叶片前缘半径、表面粗糙度、动静间隙等几何参数的随机波动以及进气压力、温度、转速等运行参数的随机波动。这些随机变量对S-CO2压缩机的气动性能具有不可忽略的影响。运行参数方面,S-CO2压缩机进口状态通常接近工质临界点,由环境温度、系统负荷等变化引起的进口状态微小变化会造成工质物性的较大变化,局部温度和压力降低还会导致亚临界状态甚至冷凝的出现,使得气动性能波动较大。
受限于试验条件的限制,国内外开展的S-CO2压缩机实验研究[3-4]和积累的实验数据较少,主要研究手段是数值模拟,通过求解雷诺平均Navier-Stokes(RANS)方程、基于物性表格插值获取S-CO2物性开展S-CO2压缩机内部流动仿真[5]和流动机理分析[6],进一步考虑相变模型[7]、非定常效应对流动的影响[8-9]。针对S-CO2压缩机靠近流体临界点运行时易出现相变的问题,国内开展了S-CO2压缩机叶顶两相流[10]、叶轮内部凝结性能分析[11],以及跨临界CO2压缩机冷凝特性[12]、进口干度与气动性能关联性分析[13],并发展了考虑S-CO2物性的多变功计算方法[14]。虽然近年来开展的一系列实验和数值研究表明S-CO2压缩机气动性能对进气参数变化的敏感性较大,目前国内外缺乏关于随机参数波动对S-CO2压缩机气动性能影响的定量研究。
准确预测S-CO2压缩机的变工况性能对于S-CO2动力循环的热力分析具有重要意义。本文对某S-CO2离心压缩机进行气动性能预测,分别采用一维经验模型方法和三维CFD仿真方法,并基于三维CFD仿真结果,采用任意多项式混沌(aPC)方法[15-16]对进口总温波动引起的S-CO2压缩机气动性能不确定性进行定量研究。
1 数值方法
1.1 一维经验模型
一维经验模型采用商业软件NREC COMPAL,压缩机叶轮采用两区模型,将叶轮内部流动分为射流区和尾迹区分别建模[17]。采用了3种扩散比建模方法:Two-Element-In-Series模型(一维模型A)、backbone curve模型(一维模型B)和hybrid function模型(一维模型C),3种方法均依赖于经验关联式,其中Two-Element-In-Series将叶轮内部分为前后两段建模,前段简化为扩压器或喷嘴,后段简化为扩压器,两段的性能通过经验给定;backbone curve模型首先通过等熵流动假定计算出理想的扩散比,然后根据经验关联式得到实际的扩散比;hybrid function模型首先参照backbone curve模型计算出扩散比,随后根据叶轮几何参数对前后两段的性能进行经验修正,以兼顾设计点和非设计点的性能预测。
1.2 三维CFD模型
三维CFD采用商业软件NUMECA/Fine-Turbo求解三维定常Navier-Stokes方程。S-CO2流体物性基于NIST数据库。空间离散采用二阶中心格式,湍流模型采用双方程k-ωSST模型,动静交界面采用混合平面法。
1.3 不确定性量化方法
考虑概率空间(Ω,Λ,Γ)内的随机过程,其中Ω为样本空间,Λ为Ω的子集,Γ为概率,对于随机函数Y=f(ξ),ξ∈Ω的一维多项式混沌展开可以写成:
(1)
其中:d为展开阶数;ci为展开系数;Ψi为正交多项式。展开系数可以由式(2)计算:
(2)
求解可采用Galerkin投影方法、配点法或数值积分法。本文采用高斯积分法计算多项式展开系数。对阶数不超过2p+1的多项式g(ξ),可以找到p+1个最佳高斯配置点ξk及权重wk,从而准确计算其积分:
(3)
与Ahlfeld等[16]的方法类似,最佳高斯配置点及权重根据随机输入参数的统计矩采用Mysovskikh[18]推导的矩阵变换关系计算得到。对于连续型随机变量ξ∈Ω,k阶统计矩μk的表达式为:
(4)
对于离散型随机变量ξ∈Ωh,假定概率密度函数为w,k阶统计矩的表达式为:
(5)
对于有ND个采样点的数据集,k阶统计矩的表达式为:
(6)
确定正交多项式的展开系数后,Y的统计信息可通过展开系数计算得到,如均值μY和方差σY的表达式为:
μY=c1
(7)
(8)
1.4 压缩机参数
本文研究了某100 kW级S-CO2离心压缩机,子午面型线如图1所示,该压缩机由叶轮和一排通道式扩压器组成。叶轮叶顶间隙为出口叶高的17%。叶轮叶片数为12,其中一半叶片为分流叶片,扩压器叶片数为18。压缩机气动设计参数列于表1,几何造型如图2所示。

表1 S-CO2压缩机设计参数

图1 S-CO2压缩机子午面型线

图2 压缩机几何造型
三维CFD计算网格如图3所示,总网格数为248万,其中叶轮通道网格数为139万,扩压器通道网格数为109万,壁面y+小于1,以便于采用低雷诺数湍流模型对近壁面流动进行求解。除该基准网格外,分别采用较粗和较密的网格开展了三维CFD计算,计算得到的流量和效率对比列于表2。由表2可见,基准网格计算得到的流量和效率与密网格的相对偏差分别为0.1%和0.07%,对于本文关注的压缩机性能参数而言,采用基准网格能够得到足够精确的结果,因此本文三维CFD计算采用图3所示的网格。

表2 不同网格数计算结果

图3 三维CFD计算网格
2 数值结果
2.1 变工况特性
一维模型在给定进出口条件后根据压缩机叶轮的进出口半径、叶高、叶片角以及扩压器进出口半径、叶高、扩张角、喉部面积等参数,基于简化模型和大量试验数据总结得到的经验关联式计算压缩机性能参数。CFD和一维模型的压缩机变工况特性曲线预测结果如图4所示。根据CFD结果,从80%到100%设计流量,压缩机效率变化低于1%,最高效率为79.2%,在93%设计流量处产生。根据一维模型A和B的计算结果,最高效率点在80%设计流量处,随后效率随流量增加而缓慢下降。根据一维模型C的计算结果,在图4中的流量范围内,效率随流量的增加而降低。随着流量的增加,CFD和一维模型的预测结果都是压比降低。总的来看,不同一维模型预测得到的效率和压比都与CFD结果有显著差异。一维模型的优势是计算速度快,但其计算结果受经验关联式影响较大,目前广泛采用的经验关联式多基于理想气体试验结果,由于目前S-CO2压缩机试验数据较为欠缺,现有商业软件中压缩机一维模型经验关联式针对S-CO2压缩机内部超临界流体流动的准确性尚未经过系统性验证;而三维CFD计算采用了更准确的几何模型,流动模型所做的简化也远少于一维模型,因此,本文开展的压缩机性能不确定性量化研究基于CFD计算结果开展。
2.2 进口温度波动影响
由于S-CO2压缩机进气参数接近工质临界点,由环境温度、系统负荷等变化引起的进口状态微小变化会造成工质物性的较大变化,从而对压缩机的性能产生影响。对于S-CO2循环系统,随着季节和区域造成的外部冷却水温度变化,压缩机进口温度也会产生变化。为了研究进口状态变化对性能的影响,本文以冷却水温度变化造成压缩机进口温度变化4 K为例,将压缩机的进口总温在设计值的基础上变化±2 K,其他参数不变,对其流动进行了定常计算。
中叶展截面的熵分布如图5所示,分别对比了设计工况和进口总温变化(ΔTt)为±2 K的结果。图5中,s/s0为基于流场中最大熵值s0归一化处理的熵。设计工况下叶轮和扩压器叶片的攻角都接近0°,进口总温增加2 K后,叶轮和扩压器都出现了较大的负攻角,扩压器叶片压力面的高损失区域增大,出现了较为明显的高熵区;进口总温减少2 K后,攻角变为正,扩压器叶片吸力面附近出现了较为明显的高熵区。可见,当进口总温变化时,在相同的压比下,压缩机内部的熵分布出现了明显的变化,反映在流场上主要是由压缩机流量变化引起了叶片攻角变化,进而造成内部流动损失的变化。

a——ΔTt=0 K;b——ΔTt=-2 K;c——ΔTt=2 K
等熵效率和流量随进口总温的变化如图6所示。进口总温增加2 K以内,等熵效率的变化幅度较小,不超过0.4%;当进口总温减小时,等熵效率大幅下降,进口总温减小2 K时下降了11.7%。与效率类似,进口总温对流量的影响也很显著。总的来说随着进口总温的增加流量减小。与设计工况相比,进口总温增加2 K时流量减少了27%,进口总温减少2 K时流量增加了62%。总的来说,当进口总温减少时,性能的变化幅度比进口总温增加时要大。
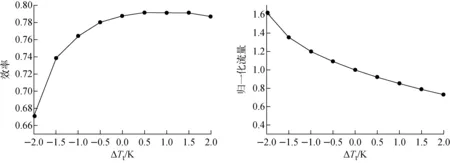
图6 压缩机气动性能随进口总温的变化
可见,进口总温变化对工质物性的影响造成了S-CO2压缩机流量产生了显著变化,从而对叶片攻角、流动损失造成了显著影响,这一影响反映在效率的变化上,这也是相对于理想工质而言,S-CO2压缩机对进口参数敏感性更高的原因。
2.3 压缩机气动性能不确定性量化
进口总温波动对S-CO2压缩机性能有着不可忽视的影响。在S-CO2循环系统中,压缩机进口状态的变化可能由环境温度、系统负荷等变化引起,必须在系统性能分析和压缩机设计中加以考虑。系统状态变化的测量数据通常是有限且离散的数据集,难以得到其真实概率密度分布函数,采用aPC方法可以基于离散数据集的统计矩进行不确定性量化分析,从而避免了拟合概率密度分布函数引起的误差。本文采用aPC方法对进口总温随机波动引起的S-CO2压缩机性能不确定性进行了量化。
进口总温的变化假定由系统状态波动引起,在±2 K的变化范围内分布了99个采集数据点,如图7所示。由于数据十分有限,很难对其概率密度函数进行准确拟合,而任意多项式方法基于数据的统计矩进行多项式展开,因此同时适用于连续分布以及离散的数据集。

图7 进口总温变化随机数据分布
由于离散数据集中每一个点的压缩机性能都可以计算得到,因此性能参数的真实统计矩可以准确计算得到,以此作为参照评价aPC方法的准确性。不同阶数aPC方法的计算误差如图8所示,采用1阶多项式展开时,效率和流量均值的计算相对误差不超过1%,当阶数增加到4阶时,相对误差不超过0.01%。效率和流量方差的计算误差总的来说大于均值,采用1阶多项式展开时,效率方差的相对误差达到73%,流量方差的相对误差达到23%。当阶数增加时,方差的计算误差降低,采用4阶多项式展开时,效率方差的计算相对误差为3.2%,流量方差的计算相对误差为2.1%。可见,采用aPC方法能够较好地预测性能参数的均值和方差,采用4阶多项式展开时,预测相对误差已达到5%以下。
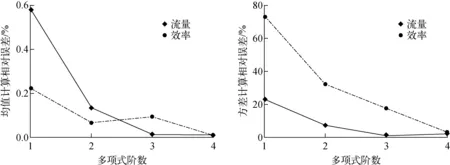
图8 不同阶数aPC方法的相对误差
3 结论
本文采用一维模型和三维CFD方法对某S-CO2压缩机进行了数值研究,一维模型预测得到的效率、压比与三维CFD计算结果存在明显差异。基于三维CFD计算结果,采用aPC方法对进口总温波动引起的S-CO2压缩机气动性能不确定性进行了定量研究,进口总温波动范围为设计工况±2 K,当进口总温降低2 K时,叶轮和扩压器攻角由0°变为-6°,导致压缩机等熵效率降低了11.7%,流量增加了62%。采用离散的测量数据集描述进口总温的随机波动时,aPC方法能够较好地预测性能参数的均值和方差。采用1阶多项式展开时,效率和流量均值的计算相对误差不超过1%,效率和流量方差的计算相对误差总的来说大于均值,采用4阶多项式展开时,效率方差的计算相对误差为3.2%,流量方差的计算相对误差为2.1%。
结果表明aPC方法能够高效准确地预测性能参数的统计信息,尤其是当随机参数的统计信息有限且离散时。本文算例中进口总温的微小变化造成了压缩机流量和等熵效率的显著变化,表明在S-CO2压缩机的设计中有必要考虑提高进气参数不确定性的稳健性,aPC方法通过定量给出参数不确定性对S-CO2压缩机性能的影响,可用于评价S-CO2压缩机对进气参数不确定性的稳健性,为S-CO2压缩机稳健性优化设计奠定基础,后续有必要进一步开展试验研究以验证本文数值模型对于S-CO2压缩机性能预测的准确性。

