CO2-SF6混合工质布雷顿循环特性初步分析

席大鹏,刘旻昀,2,刘秀婷,费俊杰,臧金光,黄彦平,*

(1.中国核动力研究设计院 中核核反应堆热工水力技术重点实验室,四川 成都 610213;2.清华大学 工程物理系,北京 100084)

二氧化碳(CO2)有合适的临界温度(31 ℃)和临界压力(7.3 MPa),良好的稳定性与化学惰性[1],储量丰富、价格便宜[2],是具有极大应用潜力与市场价值的新一代循环工质。同时CO2还有良好的中子性能,作为反应堆冷却工质具有独特的优势[3]。超临界二氧化碳(S-CO2)布雷顿循环是近年来备受学界与工业界关注的高效能量转换系统,具有设备体积小、循环设计简单等特点[4]。

S-CO2在拟临界点附近密度显著增大,可有效降低压缩功,因此使用S-CO2布雷顿循环可在保证效率的同时,降低透平入口温度,实现中等温度下的高效能量转换[5]。为保证循环效率,现有研究大多要求压缩机入口工况必须维持在临界点(31 ℃、7.38 MPa)附近,这限制了透平出口的压力与压比,阻碍了循环效率的进一步提升,也限制了S-CO2布雷顿循环在高温沙漠地区、低温深海等特殊环境中的应用。

深海核动力是先进核能系统的重要发展方向,S-CO2布雷顿循环的高效率与小体积在深海环境中应用前景广阔。低温深海环境温度低,因此可维持较低的压缩机入口温度,但受限于临界压力,压比无法进一步提升。向CO2中掺杂其余工质,降低临界压力,有望提升透平压比,获得更高效率。不同的掺杂工质、掺杂比例可获得不同的临界参数,进而适配不同的应用场景。六氟化硫(SF6)与CO2性质类似,有很好的相容性,且具有较高的密度和更低的临界压力(3.75 MPa),CO2-SF6混合工质方案在低温冷源条件下具有较大可行性[6]。

为探索CO2-SF6混合工质的应用是否能实现低温深海环境下布雷顿循环的效率优化,本文进行系统的模拟分析。首先,在实验数据的基础上,选取适当的混合工质物性计算模型,计算CO2-SF6混合物的热物性。然后,根据计算得到的热物性,计算不同组分的CO2-SF6在简单回热循环中的循环效率,并进行对比分析。

1 SF6-CO2混合工质物性模型与校验

1.1 物性计算模型

立方型物性方程与Span-Wagner物性方程[7]是目前广泛应用的两类物性预测模型。Span-Wagner物性方程基于亥姆霍兹自由能理论提出,并根据大量实验数据对参数进行了拟合,对于大量纯工质以及具有较多实验数据的常用混合工质有很高的预测精度。但CO2-SF6混合工质物性实验数据较少,缺少拟合好的Span-Wagner物性方程,若估算方程参数进行物性预测则有较大误差。

立方型物性方程是广泛用于计算物性的经典模型,具有形式简单、便于计算等优点。在用于计算混合工质物性时,立方型方程对实验数据依赖较小,仅需选取合适的混合规则及适当的相互作用系数。Yin等[6]与Haroon等[8-9]在混合工质循环研究中使用立方型方程计算物性,屠幼萍等[10]使用立方型方程对0.4～0.8 MPa下的CO2-SF6混合物露点进行了计算。立方型方程中PR(Peng-Robinson)方程使用较多,Haroon等[8-9]与屠幼萍等[10]均使用PR方程。

本文选择PR方程计算CO2-SF6混合工质物性,混合规则选取经典的范德瓦尔斯混合规则。

PR状态方程形式为:

(1)

其中:p为压力;R为通用气体常数;v为摩尔体积;T为温度;a(T)、b为与工质相关的参数,计算混合工质时需要使用混合规则根据纯工质的参数以及相互作用系数进行。

范德瓦尔斯混合规则为:

(2)

(3)

其中:i、j表示不同组分;xi、xj为摩尔分数;ai、aj、bi、bj为组分i和j的方程参数;kij为组分i与j的二元相互作用系数。

对于二元混合物,范德瓦尔斯混合规则可简化为:

(4)

b=x1b1+x2b2

(5)

其中,k为二元混合物中两种工质的相互作用系数。

1.2 相互作用系数计算模型

周伟等[11]对相互作用系数计算模型的发展进行了综述,并整理了不同模型的适用领域及误差。他们认为Nishiumi等[12]的相互作用系数计算模型适用类型广且误差小,其适用气体包含CO2、不同的烃类以及H2S,对于SF6与CO2相互作用系数的计算应有较高准确度。因此,本文选择Nishiumi等[12]的相互作用系数计算模型,其形式为:

1-kij=C+D(Vci/Vcj)+E(Vci/Vcj)2

(6)

C=c1+c2|wi-wj|

(7)

D=d1+d2|wi-wj|

(8)

其中:Vci与Vcj为两种组分的临界摩尔比体积;c1、c2、d1、d2、E为拟合参数,其具体取值与混合工质类型有关。文献中并未给出CO2与SF6混合的参数,考虑到SF6与烷烃的相似性以及硫化物分子的相似性,本文选取文献[12]中给出的CO2与小分子烷烃以及CO2与H2S的拟合参数作为待选方案,具体参数及计算得到的CO2-SF6平均相互作用系数列于表1。

表1 Nishiumi相互作用系数模型参数取值

1.3 物性模型校验

本文使用不同相互作用系数,运用PR方程与范德瓦尔斯混合规则,计算了CO2-SF6在不同密度下的压缩因子,并与实验数据进行了对比,结果如图1所示。实验数据取自黄荣荣等[13]测得的60 ℃下,不同摩尔密度时CO2-SF6的压缩因子。由图1可见,使用模型估计相互作用系数后计算得到的结果明显优于k=0时的结果。整体而言,k=0.106的结果与实验数据符合最好,在摩尔密度小于11 kmol/m3时,最大相对误差为5%,此时压力已高于12 MPa。

图1 使用不同相互作用系数计算的压缩因子与实验数据的对比

当压力高于12 MPa时,随着压力的升高,模型计算结果相对误差持续增大,因此该物性模型不再适用。在后续的循环计算中,工况控制在12 MPa。由于实验数据仅有60 ℃下的压缩因子,模型对其余物性计算的精度并未得到有效评估。但PR方程形式简单,基于深刻直观的热力学理论,且经过多年广泛使用,其对物性预测具有较好的一致性,可合理推断该模型预测其余物性也有较好的吻合度。

1.4 CO2-SF6临界性质计算

临界性质直接影响在特定应用环境下循环可选择的边界工况范围,对于循环的设计有重大影响。在深海低温环境下,冷源温度低,S-CO2布雷顿循环可将压缩机入口维持在临界点附近的高密度区,甚至可维持在亚临界温度,实现跨临界布雷顿循环。但CO2较高的临界压力限制了压比。SF6临界压力显著低于CO2,临界温度与CO2相近。CO2-SF6混合工质有望获得较低的临界压力。

本文选取k=0.106,使用PR方程与范德瓦尔斯混合规则计算CO2-SF6混合物的临界性质,如图2所示。随着SF6在混合物中所占摩尔比例的增加,混合物的临界压力近似线性单调下降,这表明CO2-SF6混合工质方案与预期相符,可获得更低的临界压力。临界温度随着SF6摩尔比例的增加先降低后升高,SF6摩尔比例小于0.6时,混合工质的临界温度较CO2纯工质低。在SF6摩尔比例约为0.23时,临界温度最低,约为296 K,较CO2临界温度低约8 K。

图2 CO2-SF6混合物临界性质

2 循环与模型

本文研究的简单回热循环基本结构如图3所示,该循环针对深海核动力应用设计。工质经过堆芯被加热,然后进入透平做功。从透平出来的乏热工质进入回热器,与刚从压缩机出来的低温工质进行热交换,实现回热。随后工质进入冷却器散热,并在压缩机中提升压力进入回热器。

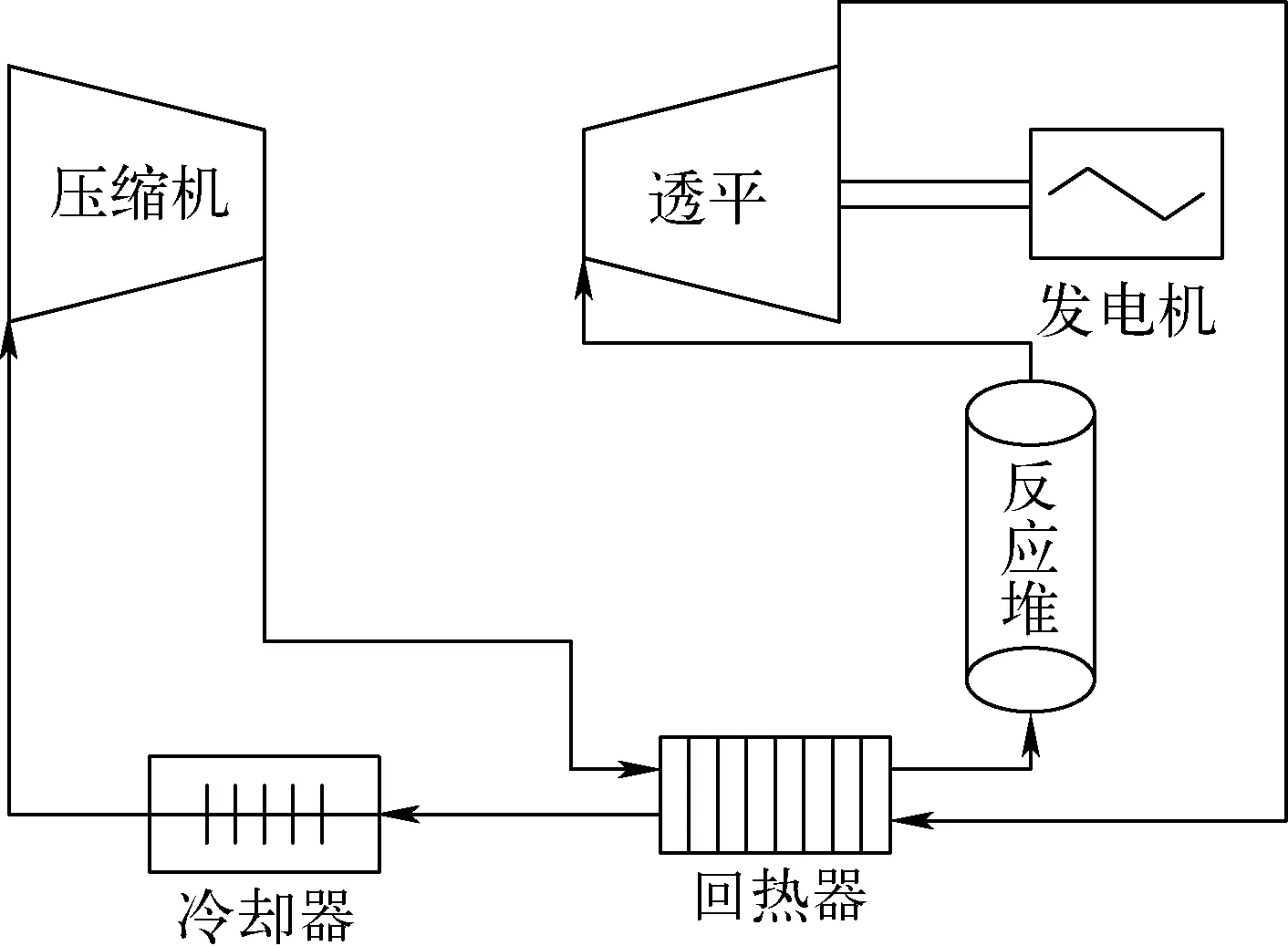
图3 简单回热循环示意图

模型对循环进行了诸多简化。各器件及连接管道的摩擦、局部压降均忽略,仅计算压缩机与透平内的压力变化;压缩机与透平使用理想等熵模型,在计算时直接指定压缩机与透平效率;换热器设定端部温差,不对内部换热过程进行详细模拟;冷却器设定工质进出口温度。

简化后的模型不需要考虑设备内部的设计细节,仅需给定设备关键设计参数;计算时仅需压力、温度、密度、焓、熵及声速等几个关键物性,不需要计算导热率与黏性系数等较难计算的输运物性。该模型简单实用,与设备的具体设计无关,仅考虑设备整体性能表现,适用于循环初步设计筛选。

模型输入为压缩机入口压力、透平入口压比、透平入口温度、额定电功率以及辐射换热冷源温度;模型输出为循环实际热功率、压缩机耗功以及部分设备尺寸等。模型计算时使用的部分设备常量参数列于表2。

表2 循环计算模型常量参数

深海环境温度大多在4 ℃附近,因此冷却器热阱温度设置为4 ℃。循环中热源为直接循环S-CO2反应堆,其出口条件多采用麻省理工学院提出的S-CO2反应堆设计参数(550 ℃,20 MPa)[14]。但考虑到本文物性模型仅适用于12 MPa以下工况,因此将透平入口压力设置为12 MPa。

3 循环模拟结果

本文研究的简单回热循环给定透平入口温度与入口压力,影响循环效率的主要边界参数为压缩机入口温度与入口压力。压缩机入口条件的选取与混合工质的临界性质有关,本文研究了SF6摩尔比例为0.00～0.45的情形,压缩机入口压力设置为较临界压力高0.1 MPa,压缩机入口温度则设定为15～55 ℃,覆盖了本文研究的所有组分的CO2-SF6的临界温度。模拟工况分类列于表3,其中0组为纯CO2工质,作为其余组的对照组。

表3 不同组分模拟工况分类

图4为不同组的循环效率计算结果。由图4可看到,随着SF6摩尔比例的增加,循环效率在所有温度下均有提升,在SF6摩尔比例达到0.25后,效率提升不再明显。对于单个组分的效率曲线,随着压缩机温度的降低,效率先逐渐升高,当接近拟临界温度时,效率到达到拐点并在拟临界温度附近出现骤变。低于拟临界温度时的循环效率显著低于高于拟临界温度时的。由于掺杂SF6后临界温度降低,最优循环温度随之降低。纯CO2工质循环效率在39 ℃时达到最高,在SF6摩尔比例为0.25时,循环效率最大值发生在25 ℃处。

图4 不同组分的循环效率对比

不同组分间的循环效率差异来源于不同的压比,掺杂SF6的混合工质有着更低的临界压力,可实现更低的压缩机入口压力。为验证压比对循环效率的影响,本文针对SF6摩尔比例为0.25的工况进行了不同压比下的循环效率计算,并与纯CO2工质进行了对比。模拟工况参数列于表4,模拟结果如图5所示。由图5可看到,随着压比的下降,混合工质循环效率逐步下降至与纯CO2工质同一水平甚至更低,混合工质的优势主要来源于压比的提升。由于在较高压力下,SF6摩尔比例为0.25的混合工质在拟临界区的物性畸变减弱,其循环效率曲线趋于平滑,在低于拟临界温度的低温区,混合工质始终具有显著优势。分组3-f与纯CO2工质使用相同的压缩机入口压力7.477 MPa,在高温下的循环效率明显低于纯CO2工质,但在低于拟临界温度的低温区,其效率依然显著高于纯CO2工质,这表明CO2-SF6混合工质在压缩机入口温度较低时循环效率随温度、压力的波动显著低于纯CO2工质。

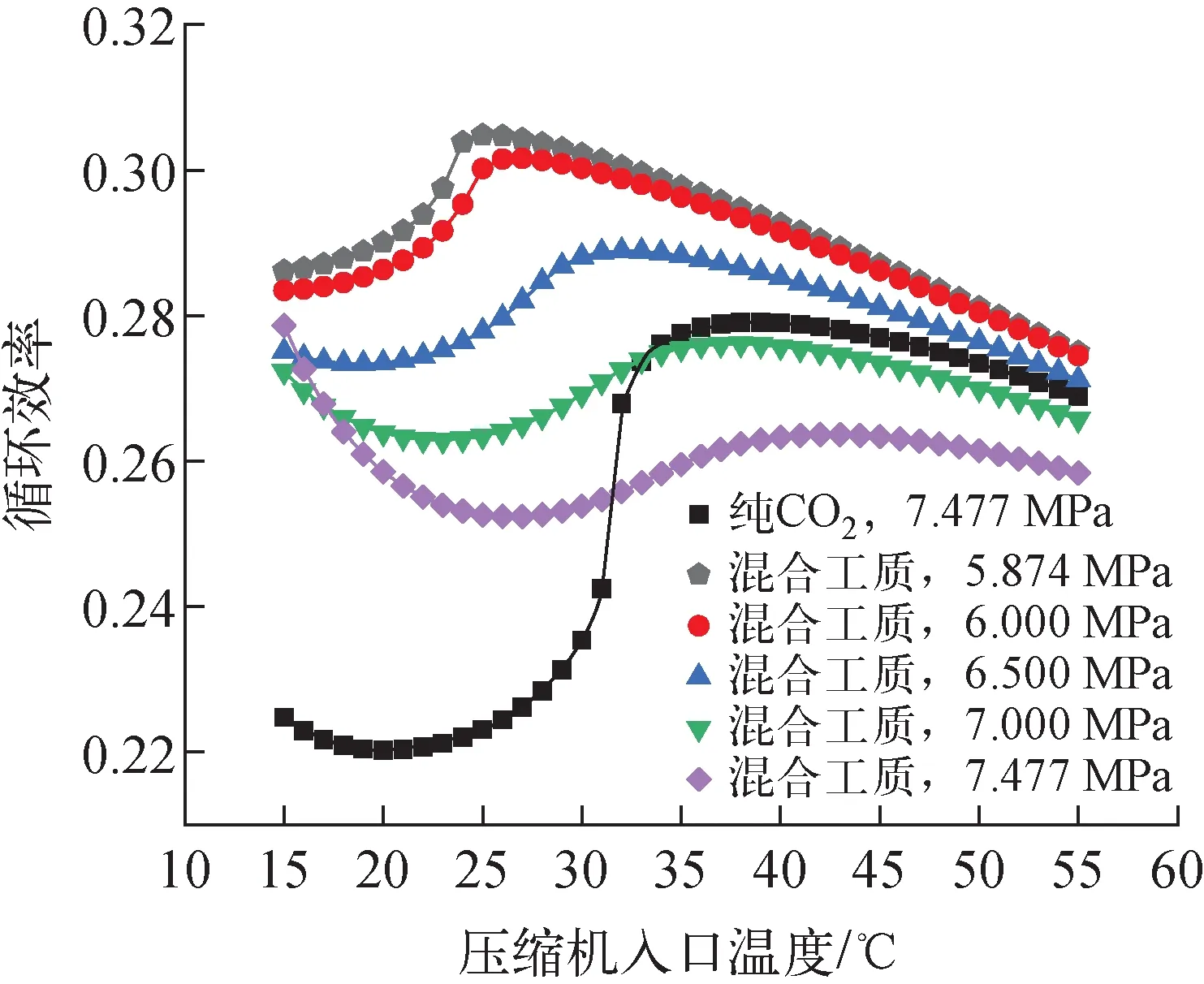
图5 不同透平压比的循环效率对比

对于单个组分,循环效率随压缩机入口温度的变化主要由压缩功与向冷源散热量的变化导致。表3所列不同分组的压缩功随温度的变化如图6所示。从图6可看到,随着压缩机入口温度的降低,压缩功明显降低,且不同组分工质降低幅度基本一致。在压缩机入口压力下,表3所列不同组分在压缩机入口处焓值随温度的变化示于图7。可看到,随着温度的降低,压缩机入口焓值降低,并且在跨过拟临界温度时有大幅跃变。焓值变化幅度随SF6摩尔比例的增加而减小。压缩机入口焓值低意味着更多的热量流向了冷源,会导致效率下降。在这两方面因素的影响下,最终循环效率如图4所示。当压缩机入口温度低于拟临界温度时,效率会明显降低,这是因为跨过拟临界区损失了大量热能,SF6摩尔比例的增加能有效缓解甚至消除压缩机入口温度跨临界时的循环效率下降。而当温度高于拟临界点一定值后,随着温度的升高,循环效率下降,这是因为此时压缩功的升高主导了循环效率的变化。

图6 不同组分压缩功随温度的变化

图7 不同组分压缩机入口焓值随温度的变化

综合而言,对于简单回热循环,使用CO2-SF6混合工质代替纯CO2工质可有效提升透平压比,进而提升循环效率,但当SF6摩尔比例高于0.25后,效率提升不明显。对于单个组分,给定压缩机入口压力后,存在最优压缩机入口温度。当压缩机入口温度低于拟临界温度时,循环效率会大幅下降,使用CO2-SF6混合工质可有效改善循环效率下降的问题,提高循环在低温冷源下的稳定性。

4 结论

本研究使用PR方程计算了CO2-SF6混合工质的物性,并使用计算得到的物性对混合工质简单回热循环效率进行了模拟计算分析。其中物性计算使用PR方程结合范德瓦尔斯混合规则,混合规则中相互作用系数由Nishiumi等[12]的相互作用系数计算模型得到。物性模型使用文献实验数据进行了校验,在12 MPa以下吻合良好。简单回热循环的模拟计算使用简化的集总参数模型,仅考虑关键设备的出入口条件等关键设计参数,方便对循环进行快速初步筛选。主要结论如下:

1) Nishiumi相互作用系数模型预测的相互作用系数用于CO2-SF6混合工质物性计算效果较好,推荐使用其针对CO2/H2S混合工质拟合的参数;

2) 对于简单回热循环,使用CO2-SF6混合工质代替纯CO2工质可有效提升透平压比,进而提升循环效率,并且由于临界压力降低,最优循环温度也会降低;

3) 当压缩机入口温度低于拟临界温度时,由于在向冷源散热时跨过拟临界区损失大量热能,循环效率会大幅下降,对于简单回热循环,在低温环境下进行功率负载调整时应同步调整冷源冷却效果,如减少冷却水流量,避免压缩机入口温度过低;

4) 使用CO2-SF6混合工质可有效改善压缩机入口温度低于拟临界温度时循环效率下降的问题,提高循环在低温冷源下的稳定性。