Taylor撞击塑性变形的尺寸效应研究
沈子楷,戴湘晖,王可慧,钱秉文,范如玉,高鹏飞,柯 明,周 刚
(1.清华大学 工程物理系,北京 100084;2.西北核技术研究所,西安 710024)
结构动态响应是冲击动力学领域中非常重要的研究内容,例如爆炸条件下的结构损伤,撞击对工程防护结构的毁伤破坏等。其中,实验/试验研究是必不可少的研究手段。然而在冲击条件下大尺寸结构的动态响应试验研究中,由于经费、时间周期、试验难度等的制约,大多数采用小尺寸缩比模型开展实验研究,再放大到原型试验。根据相似理论,当小尺寸模型实验和大尺寸原型试验的所有相似条件都满足时,模型和原型才完全相似。但由于物理法则、实验方法和材料性质等因素的限制,相似条件无法完全满足,导致小尺寸模型实验和大尺寸原型试验不能完全相似,产生尺寸效应。
对于结构动态响应的相似性和尺寸效应问题,Bazant等[1]在其关于尺寸效应的综述文章中,较为全面地总结了结构失效的尺寸效应方面的研究进展,讨论了尺寸效应的三种主要类型,包括随机性导致的强度统计尺寸效应、能量释放的尺寸效应以及断裂或微裂纹产生的尺寸效应,还概述了率相关的材料行为。白以龙[2]讨论了分布式损伤失效及其尺寸效应问题,需要将宏观和微-细观耦合起来,来研究跨尺度的尺寸效应机理。张守保等[3]认为应变率效应、断裂韧度、损伤积累和不同耗能机制是影响侵彻爆炸实验中结构响应相似性的关键因素,为了减小尺寸效应的影响,缩比一般不应超过1/8。Scott等[4-5]认为对于缩比仅为几分之一的模型来说,应变率效应导致的尺寸效应可以忽略。Oshiro等[6-7]提出了一种考虑应变率效应的近似相似方法,在模型和原型之间建立一个过渡模型,通过调整冲击速度,抵消应变率的影响,使得过渡模型和原型相似。Zhang等[8-10]通过对加筋板结构在水下爆炸冲击波作用下相似问题的研究方法进行扩展,提出了加筋板结构在水下爆炸冲击波作用下动态响应的相似条件。田常津等[11]对撞击穿甲的缩比模型实验进行了初步的定量分析,认为应变率因素使模型的变形量偏小,在缩比率1/2时可增加10%来估算原型的变形量。刘源等[12]通过对非等比例缩比侵彻相似规律进行研究,提出了非等比例缩比相似方法,使得弹体刚体过载相似。王帅等[13-14]通过缩比模型和原型的动态屈服应力在一定应变率区间上的最佳逼近,获得修正尺寸效应的比例因子,使得模型和原型相似。在结构动态响应问题中,Taylor撞击问题是一种典型情况,早期人们常通过测量圆柱杆撞击刚性靶后的变形来反推材料的动态屈服强度[15-17]。近年来,Taylor撞击实验又重新引起了研究人员的重视,人们发现,通过一次Taylor撞击实验,杆中的非均匀变形提供了不同大小应变、不同量级应变率下的本构响应等信息,可以十分有效地用于研究、验证材料的本构模型[18-19]。一般来说,对于不同的Taylor杆尺寸,应变率不同,材料强度不同,反映为Taylor杆变形不同,据此可以得到不同应变率下材料的动态屈服强度或详细的本构模型。从尺寸效应的角度来说,通过对不同缩比尺寸下的Taylor撞击进行研究,简化了结构响应模式,尤其对于弹体侵彻靶板这一动力学过程来说是一种特例,即靶板为刚性,Taylor杆撞击后发生变形,侵彻深度为零,可以对导致尺寸效应的多种主要因素进行解耦,研究应变率效应的影响。
前人对结构响应的尺寸效应问题已进行了很多有益探索,但大多数为定性分析,缺少定量的认识,缩比模型实验和原型试验结构响应的偏差或为简单估算、或通过仿真来研究确定,缺乏系统的实验支撑,而且由于影响相似性的因素相互耦合,难以对尺寸效应进行准确描述。本文对Taylor撞击过程中的相似性和尺寸效应展开了分析,建立了考虑尺寸效应的Taylor杆变形公式,通过系统开展不同缩比尺寸下的Taylor撞击实验,采用直接测量、三维扫描分析、SEM(扫描电子显微镜)微观分析的方法,定量比较了Taylor杆变形的尺寸效应,明确了不同缩比尺寸下的结构响应偏差。结果表明,由于应变率因素,Taylor撞击变形存在明显的尺寸效应,在相同实验条件下,Taylor杆尺寸越小,应变率越高,无量纲塑性变形越小。
1 Taylor撞击相似性和尺寸效应分析
1.1 Taylor撞击相似性分析
对于结构响应问题,以Taylor撞击产生塑性变形为例,其变形量,如长度,与主要影响因素的函数关系可以写为
ΔL=f(L,D;σ,E,λ,K,ρ,g;v0,α,φ)
(1)
式中:第一部分为几何相似条件,L、D为轴向和横向特征尺寸;第二部分为物理相似条件,σ、E、λ、K、ρ为强度、杨氏模量、泊松比、断裂韧度、密度,g为重力加速度;第三部分为初始条件,v0为弹体着靶速度,α为弹着角,φ为弹体攻角。
以L、ρ和v0作为基本物理量,式(1)可以写成如下无量纲形式
(2)
取相似参数
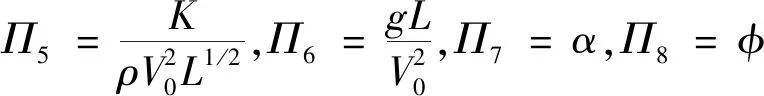
(3)

(4)
式中:下标p为原型(prototype);下标m为缩比模型(model)。
1.2 Taylor撞击尺寸效应分析
式(2)中,若缩比模型实验和原型试验相比,应变率效应导致的强度变化不可忽略,则缩比模型实验和原型试验的相似参数Π2之比
(5)
由相似理论,缩比模型实验和原型试验不完全相似,体现到式(2)中,有
(6)
(7)
利用Taylor撞击变形理论,也可以得到相同的结果。根据Taylor杆变形的表达式[20]
(8)
式中:σY为动态强度;e0为工程应变。
对于Taylor杆的最终长度,有
Lf=L0(1-e0)[1-ln(1-e0)]
(9)
式中:L0、Lf分别为Taylor杆的初始长度和最终长度。
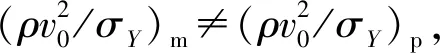
1.3 考虑尺寸效应的Taylor撞击变形理论模型
考虑动态屈服强度的应变率强化效应,例如采用Cowper-Symonds模型
(10)
式中:σ0为静态屈服应力;C和p为材料参数。
假设长度方向上应变率和速度与长度的比值成正比
(11)
则可以得到考虑尺寸效应的Taylor杆无量纲变形表达式
(12)
式中,A=(a/C)1/p。
式(12)表明,Taylor杆的无量纲变形除了和Taylor杆的速度、密度、准静态屈服强度有关,还和Taylor杆的尺寸有关。
2 Taylor撞击实验
2.1 实验方法
实验采用正向撞击方式,如图1所示,以Φ20 mm口径气炮作为发射装置,使用一定压力的氮气/空气作为发射气体。通过压缩机将氮气/空气压缩并储存到气室内,发射时打开阀门,气体快速膨胀做功,推动弹体达到一定速度,撞击固定的高强度靶板。为了便于回收Taylor杆,提高实验安全性,靶板置于靶箱中,并在靶箱中铺设橡胶垫,防止Taylor杆和靶箱发生二次碰撞,产生干扰实验结果的变形破坏。
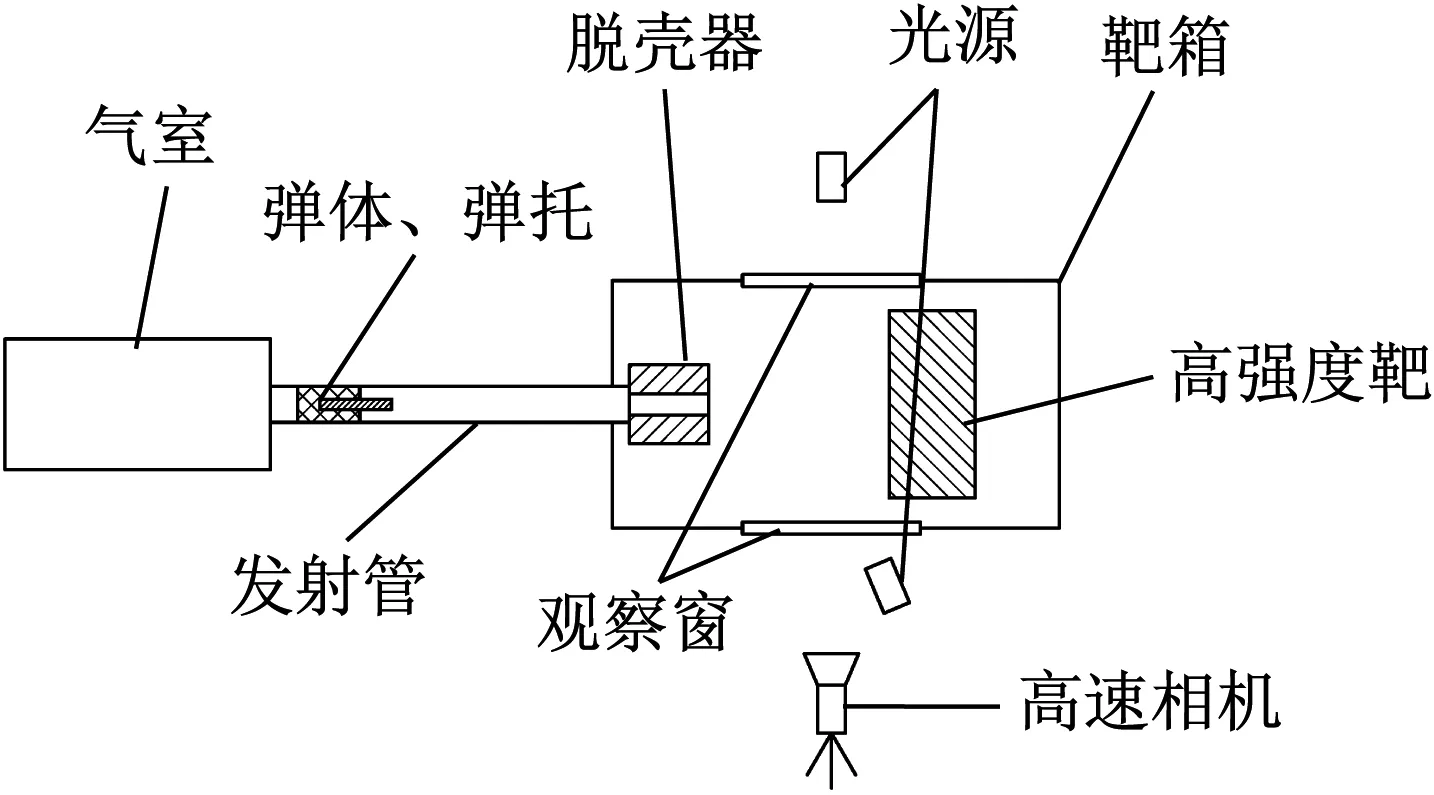
图1 Taylor撞击实验示意图Fig.1 Schematic diagram of Taylor impact test
2.2 试验技术状态
Taylor杆材料采用Q235B钢,选用4种尺寸,长径比均为8∶1,Taylor杆实物如图2所示,结构参数如表1所示。
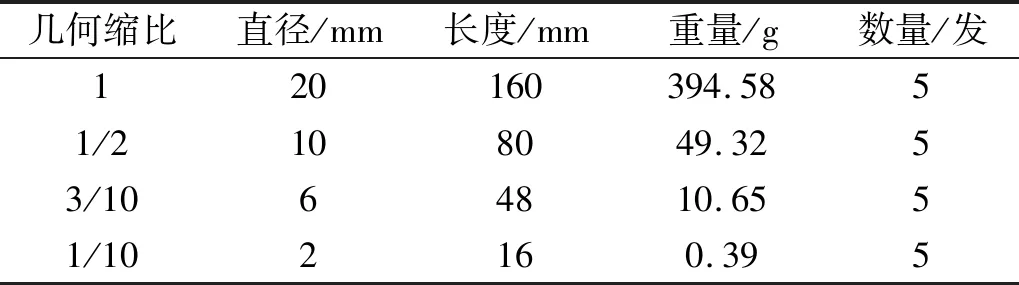
表1 Taylor杆结构参数Tab.1 Taylor bar structure parameters

图2 不同尺寸的Taylor杆Fig.2 Taylor bars of different sizes
为了消除弹托对Taylor杆弹体变形的影响,Φ20 mm×160 mm尺寸的Taylor杆采用满口径发射,其余尺寸弹体采用次口径发射、脱壳,发射状态如图3,在炮口放置脱壳器见图1。脱壳器中间通孔的直径略大于Taylor杆直径、小于弹托的外径,发射后仅Taylor杆从脱壳器通孔中间穿过,弹托被阻挡下来,使得仅有Taylor杆撞击靶板,防止弹托质量的不相似影响Taylor杆撞击变形的相似性。

(a) Taylor杆直径20 mm
2.3 实验情况
高速相机拍摄到的Taylor杆撞靶变形过程如图4所示。Taylor杆高速撞击靶板,头部质点速度立即减小为零,尾端以初始速度继续向前移动,Taylor杆整体长度减小,头部发生塑性流动、镦粗,直径变大,随后塑性区向Taylor杆尾端扩展,直径变化量逐渐减小、塑性变形减小,未变形段长度逐渐减小,直至尾端速度减小为零,变形结束。

图4 Taylor杆撞靶变形过程Fig.4 Process of Taylor bar impacting rigid target
回收得到的不同尺寸的Taylor杆如图5所示,典型的Taylor杆头部变形情况如图6所示。

图5 回收的Taylor杆状态Fig.5 Recovery of Taylor bars

图6 典型的Taylor杆头部变形情况Fig.6 Typical deformation of Taylor bar’s head
为了判断Taylor撞击是否为正撞击,无攻角、倾角,将Taylor杆非撞击端贴合游标卡尺一端,观察Taylor杆撞击端平面和游标卡尺另一端之间的光缝,测量撞击端平面和非撞击端平面之间的夹角。从实验结果看,Φ20 mm×160 mm、Φ10 mm×80 mm和Φ6 mm×48 mm的Taylor杆撞击后存在微小的不对称性,综合分析认为小的撞击攻角对Taylor杆变形特征尺寸影响不大[21],可以暂不考虑撞击攻角和撞击倾角对Taylor杆变形的影响;Φ2 mm×16 mm的Taylor杆由于质量太小、脱壳时的扰动对撞击姿态影响较大,撞击靶板时攻角对撞击变形的影响不可忽略,导致Taylor杆侧向弯曲、变形模式发生改变,在后续Taylor杆正撞击塑性变形尺寸效应的比较分析中不考虑Φ2 mm×16 mm的Taylor撞击数据。
另外,编号D10-4的Taylor杆的撞击速度较高,为324.13 m/s,头部开裂,如图7所示。Taylor撞击变形模式和能量转化分布发生了变化,在后续的相似性分析中,仅研究Taylor杆的塑性变形,暂不考虑头部开裂的情况。编号D20-3的Taylor杆撞击速度较低,为81.38 m/s,也暂不考虑该发数据结果。

图7 编号D10-4的头部开裂Fig.7 Head cracked phenomenon of number D10-4
3 Taylor撞击实验结果及尺寸效应分析
3.1 Taylor撞击实验结果
撞击后的Taylor杆变形特征尺寸如图8所示。平行于Taylor杆非撞击端,测量Taylor杆的最终长度Lf;对于撞击端面,为了进一步减小非对称撞击的影响,测量撞击端面的最小直径作为撞击端最终直径Df;使用游标卡尺测量非撞击端直径并锁止,向撞击端滑动直至无法移动,即直径开始变大的地方,以此作为未变形段,测量该段长度作为未变形段长度xf,另记Taylor杆初始长度为L0,初始直径为D0,初始撞击速度为v0,结果如表2所示。
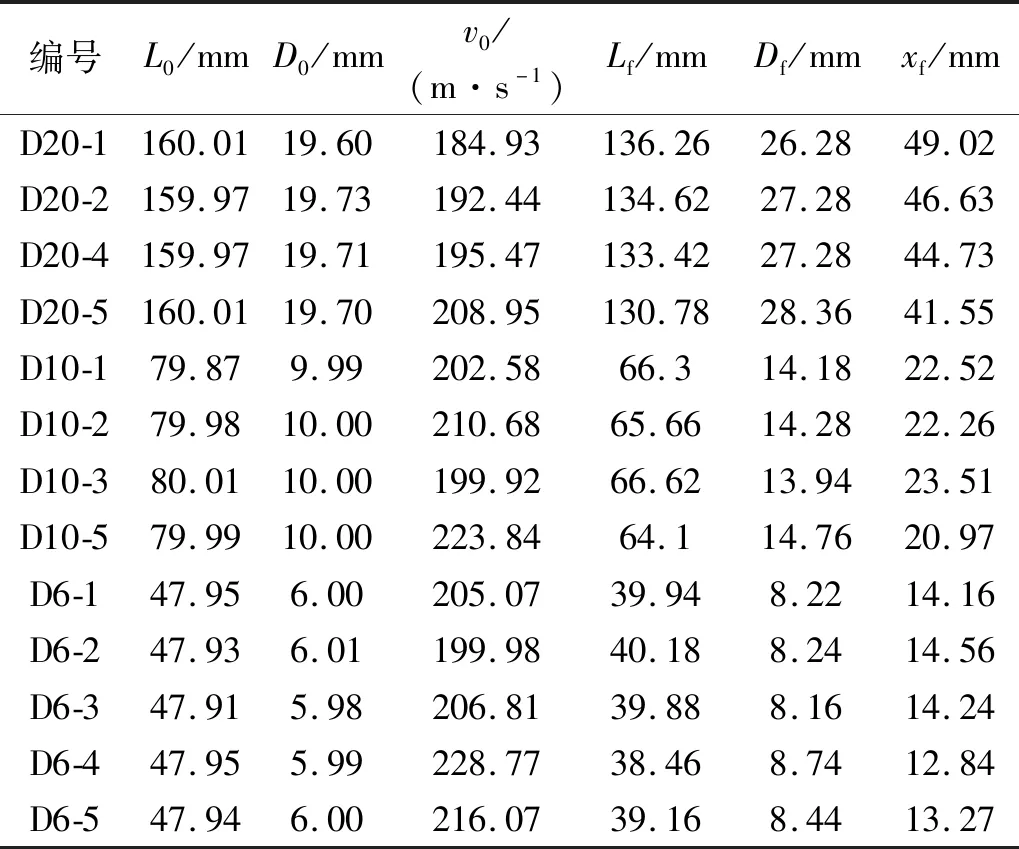
表2 Taylor撞击实验结果Tab.2 Result of Taylor impact test

图8 Taylor杆变形示意图Fig.8 Schematic diagram of Taylor bar’s deformation
使用手持式激光三维扫描系统,对Taylor杆变形进行三维扫描和重构,并和撞击前的Taylor杆进行3D比较,得到Taylor杆的变形情况,以D20-5为例,如图9所示。

(a) 撞击后的三维外形
3.2 Taylor杆变形尺寸效应
根据实验测量结果,计算无量纲长度变化量(Lf-L0)/L0、无量纲直径变化量(Df-D0)/D0和无量纲未变形段长度xf/L0,结果如表3所示。不同尺寸下Taylor杆变形的无量纲量和速度的关系如图10所示。
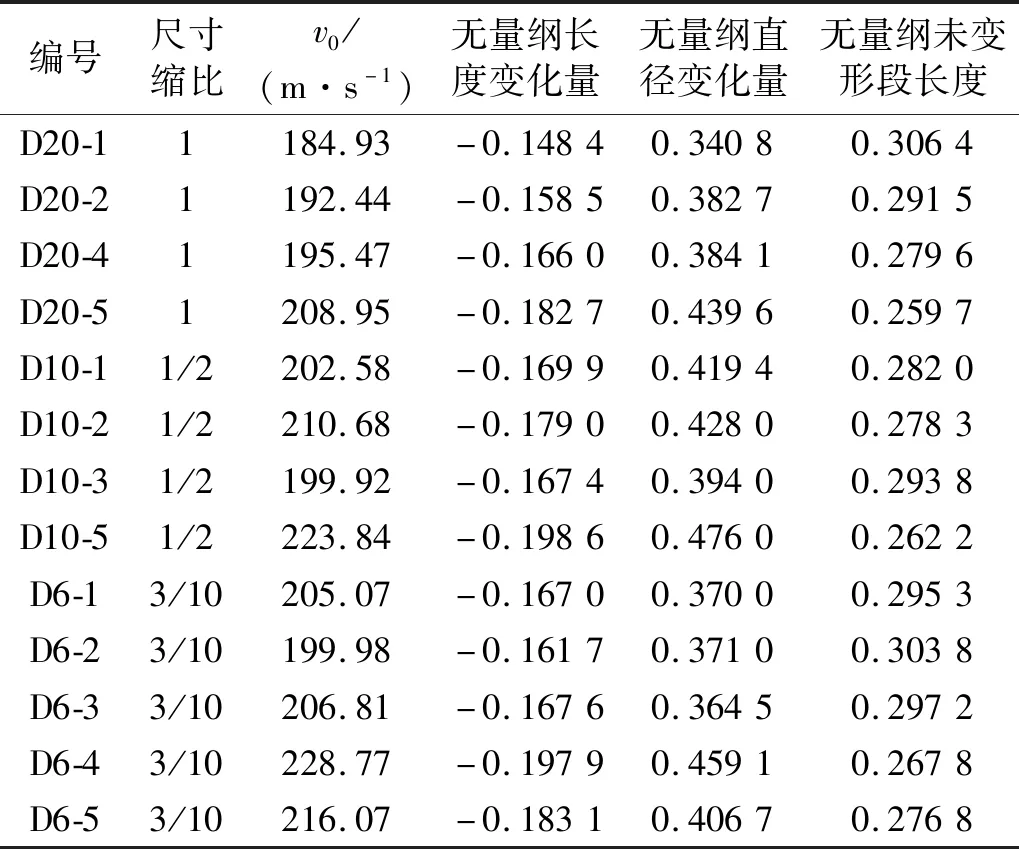
表3 不同尺寸下Taylor撞击实验的无量纲结果Tab.3 Dimensionless result of Taylor impact test at different sizes

(a) 无量纲长度变化量
可以看出,不同尺寸的Taylor杆变形规律基本相同,但又存在一定差异。在图10中直观表现为,尺寸减小,Taylor杆变形情况向右偏移。
以D20-5、D10-2、D6-3的无量纲变形量为例,尺寸缩比分别为1、1/2、3/10,撞击速度条件较为接近,小尺寸缩比Taylor杆的无量纲变形量和大尺寸原型Taylor杆的无量纲变形量的偏差如表4所示。尤其是小尺寸的D10-2撞击速度高于大尺寸的D20-5,但是其无量纲变形量反而较小,明显体现了Taylor撞击的尺寸效应。

表4 D20-5、D10-2、D6-3的无量纲变形量和偏差Tab.4 Dimensionless deformation and deviation of D20-5,D10-2 and D6-3
需要对实验测量的不确定度进行分析,由于实验中存在一些无法测量、难以确定、不能排除的小扰动,影响Taylor杆最终的变形情况,对撞靶速度测量的不确定性、撞靶姿态的不确定性开展分析,速度测量偏差1~2 m/s、撞靶攻角偏差1°,对于直径变形量带来的影响分别约为1.2%、4.6%[22],另外在小攻角条件下撞靶攻角对Taylor杆长度变形的影响小于对直径变形的影响,因此认为Taylor撞击实验中的不确定性不会影响Taylor杆塑性变形存在尺寸效应这一基本判断。另外,为了消除速度偏差和实验偶然因素的影响,对各个尺寸下200 m/s速度附近的实验数据进行拟合插值,将Taylor杆塑性变形统一为撞击速度200 m/s时的实验结果,对数坐标系下无量纲最终长度Lf/L0、无量纲撞击端直径Df/D0、无量纲未变形段长度xf/L0和速度的关系,如图11所示。

(a) 无量纲最终长度
由图11可知,在相同尺寸下,撞击速度越高,Taylor杆变形越大;在相同撞击速度下,Taylor杆尺寸越小,无量纲长度变化量的绝对值越小、无量纲直径变化量越小、无量纲未变形段长度越大,即变形量越小;在相同无量纲变形量的情况下,Taylor杆尺寸越小,所需要的撞击速度越高,即上述的小尺寸Taylor杆变形的右移特征,Taylor杆塑性变形存在明显的尺寸效应。
根据图11拟合的200 m/s撞击速度下Taylor杆的无量纲最终长度、无量纲撞击端直径和无量纲未变形段长度,计算得到小尺寸Taylor杆(尺寸缩比分别为1/2、3/10)和原型Taylor杆(尺寸缩比为1)变形的偏差如表5所示。以无量纲长度变化量为例,3∶10缩比Taylor杆的无量纲长度变化量绝对值与1∶1原型的偏差为-7.25%,也就是说,若通过开展3∶10缩比Taylor撞击实验,将实验结果按照几何相似放大到1∶1原型实验,推得的原型Taylor杆长度变化量绝对值将偏小7.25%。精细来看不能将小尺寸Taylor撞击实验结果按照比例简单外推至大尺寸实验,尤其是缩比倍数较大时。

表5 200 m/s速度下不同尺寸Taylor杆的无量纲变形量和偏差Tab.5 Dimensionless deformation and deviation of Taylor bar at different sizes with impact velocity of 200 m/s
根据激光三维扫描结果,将变形后的D20-5、D10-2、D6-3缩放到相同大小(直径、长度分别除以各自的初始直径、初始长度进行无量纲化),比较Taylor撞击实验后撞击端整体形状的相似性和尺寸效应,如图12所示。

图12 撞击实验后D20-5、D10-2、D6-3的无量纲形状比较Fig.12 Comparison of dimensionless shape of D20-5,D10-2 and D6-3 after impacting
由图12可知,在相近撞击速度下,不仅是撞击端面这一位置处的直径变化,Taylor杆整体变形均存在一定的尺寸效应,小尺寸缩比Taylor杆的无量纲变形在各个位置处均小于大尺寸原型Taylor杆。此外,采用激光三维扫描测量得到的Taylor杆变形值和表2直接测量得到的变形值一致。
使用尺寸相关的Taylor杆变形公式(12),对实验数据进行拟合,来研究分析尺寸效应对Taylor杆无量纲变形的影响。
以Taylor杆无量纲最终长度为例,使用不同尺寸、不同速度下的各个Taylor杆变形数据,取Taylor杆材料Q235B钢的密度ρ=7.85×103kg/m3、准静态屈服强度σ0=235 MPa,拟合得到考虑尺寸效应的表达式
(13)
式中:A=1.083 s0.090 05;e0=F-1(Lf/L0);Lf/L0=F(e0)=(1-e0)[1-ln(1-e0)]。
使用式(13),计算不同尺寸下的Taylor杆无量纲最终长度和初始撞击速度的关系如图13所示。

图13 Taylor杆无量纲最终长度和初始撞击速度的关系Fig.13 The relationship between the dimensionless final length of the Taylor bar and the initial impact velocity
同样的,使用式(13)可以计算得到小尺寸Taylor杆(尺寸缩比分别为1/2、3/10、1/10)和原型Taylor杆(尺寸缩比为1)变形的偏差,如表6所示。

表6 200 m/s速度下不同尺寸Taylor杆的无量纲长度变化和偏差Tab.6 Dimensionless final length and deviation of Taylor bar at different sizes with impact velocity of 200 m/s
由表6可知,在200 m/s撞击速度下,缩比模型尺寸为原型尺寸的1/10时,缩比模型的无量纲长度变化量为原型的88.22%,长度变形偏小11.78%,即若通过开展1∶10缩比Taylor撞击实验,将实验结果按照几何相似放大到1∶1原型实验,推得的原型Taylor杆长度变化量绝对值将偏小11.78%,低估了大尺寸原型Taylor杆的变形。
综合上述分析,对于小尺寸缩比模型,其缩比尺寸越小,会导致应变率越高,Taylor杆的动态屈服强度越高,塑性变形减小,造成尺寸效应,使得由小尺寸缩比模型塑性变形推及大尺寸原型塑性变形的偏差越大。在结构动态响应的研究中应当考虑应变率效应导致的尺寸效应,对于强度考核实验,尤其是临界状态下,小尺寸缩比模型的结构强度满足要求,不一定能够确保大尺寸原型的结构强度满足要求,若不考虑尺寸效应,可能会导致错误的考核结果,在大尺寸原型结构的应用中造成无法挽回的损失。
3.3 SEM微观分析
为了进一步分析Taylor杆变形和尺寸效应在微观下的体现形式,在D20-5和D6-3的相同比例部位取样进行SEM微观分析,取样位置如图14所示,其中D20-5-a、D6-3-a为未撞击变形端取样点,可以作为初始状态;D20-5-b、D6-3-b为撞击变形端取样点,比较在相同速度、不同尺寸、不同应变率条件下,结构材料的无量纲微观变形情况和尺寸效应。Q235B钢典型的SEM扫描结果,可以看到明显的铁素体和珠光体形貌特征,如图15所示。

(a) D20-5
D20-5和D6-3撞击端和非撞击端SEM扫描结果如图16所示,D20-5的珠光体呈片状分布,D6-3的珠光体呈层状分布,这是因为片状珠光体在不同方向上的切片导致。以珠光体间距作为特征尺寸,即把珠光体视为标记点,比较珠光体间距变化的尺寸效应。切片方向的不同虽然会影响珠光体的初始间距,尤其是对于径向方向,但对于各项同性材料来说,基本不会影响珠光体间距变化的应变值。采用统计平均的方法,分别得到D20-5和D6-3的未撞击变形处和相同比例位置撞击变形处(距离撞击端面长度/Taylor杆初始长度=0.012 5)的轴向、径向方向珠光体的平均间距,并计算珠光体间距变化的应变值,结果如表7所示。

表7 D20-5、D6-3撞击端珠光体间距变化Tab.7 Variation of pearlite spacing at impact end of D20-5 and D6-3

(a) D20-5-a
由图16可知,在撞击端,珠光体的轴向受到压缩,尺寸减小,径向尺寸增大,珠光体变得细长。根据表7的结果,在相近撞击速度下,D6-3和D20-5相比,尺寸缩比为3/10,D6-3珠光体轴向、径向间距变化的应变值的绝对值均小于D20-5,即小尺寸Taylor杆的无量纲变形量小,从微观上看Taylor杆变形存在明显的尺寸效应。
若沿变形后Taylor杆轴向和径向的多个点进行微观SEM扫描分析,测量得到应变分布,则可以计算得到Taylor杆的宏观变形情况。
以轴向变形为例,设应变分布为
εl=f(z),0≤z≤Lf
(14)
取一个小微元,其初始长度为dl,变形后长度为dz,该位置处的长度方向应变为
(15)
即
(16)
积分可以得到
(17)
在本问题中,假设轴向应变在Taylor杆变形段中为线性分布,见式(18),曲线如图17所示,其中,横坐标z表示距离撞击端面的距离,纵坐标εl表示轴向应变,撞击端面处轴向应变为ε0。

图17 Taylor杆轴向应变分布曲线Fig.17 Axial strain distribution curve of Taylor bar
(18)
将式(18)代入式(17)中,得到Taylor杆宏观变形和撞击端面处轴向应变的关系
(19)
由D20-5和D6-3的宏观变形情况预测得到的撞击端处的轴向应变,如表8所示。

表8 由宏观变形情况预测撞击端处轴向应变Tab.8 Prediction of axial strain at impact end by macro-deformation
表8的预测结果和表7中由SEM扫描结果计算得到的应变值在量级和规律上基本一致,其偏差的主要来源一方面是轴向应变线性分布的假设,由于表8中的应变绝对值大于表7,因此线性分布假设低估了Taylor杆的变形,推测实际的应变分布为下凸的曲线,而不是直线;另一方面是SEM扫描图像中珠光体间距统计计算的偏差,其中还存在着变形过程中珠光体的破碎细化等因素。从不同尺寸应变结果的规律上可以看出,D20-5的撞击端部变形大于D6-3,存在尺寸效应。
4 结 论
本文采用相似理论和Taylor杆变形理论对Taylor撞击结构响应的尺寸效应进行了分析,通过引入尺寸、速度对应变率的影响,得到了尺寸相关的Taylor杆变形公式,系统开展了不同缩比尺寸下的Taylor撞击实验,结合Taylor杆变形测量结果、三维扫描结果和SEM图像,对Taylor撞击过程中的尺寸效应进行了量化表征。主要结论如下:
(1) 建立了考虑尺寸效应的Taylor杆变形理论解析模型,表明Taylor杆的无量纲变形除了和Taylor杆的速度、密度、准静态屈服强度有关,还和Taylor杆的尺寸有关,结合实验结果拟合获取相关参数,公式计算结果和不同尺寸、不同速度下的Taylor撞击实验结果吻合较好。
(2) 在1/2缩比、3/10缩比条件下,Q235B材料Taylor杆以200 m/s撞击固定的高强度靶板,其无量纲长度变化量与原型的偏差分别为-3.75%、-7.25%,无量纲直径变化量与原型的偏差分别为-5.66%、-15.23%,无量纲未变形段长度与原型的偏差分别为7.17%、11.78%。
(3) 采用激光三维扫描成像可以还原Taylor杆的形状,根据扫描结果,不同尺寸下Taylor杆塑性变形形状基本一致,但存在一定的尺寸效应,从宏观上看小尺寸缩比Taylor杆各个位置处的无量纲变形量均小于大尺寸原型Taylor杆。
(4) 小尺寸Taylor杆的珠光体间距相对变化量小于大尺寸Taylor杆,从微观上看Taylor杆变形也存在明显的尺寸效应。若沿变形后Taylor杆轴向和径向的多个点进行微观SEM扫描分析,测量得到应变分布,则可以计算得到Taylor杆的宏观变形情况。通过对Taylor杆轴向应变分布的分析,也可以由Taylor杆宏观变形情况预测得到撞击端面的轴向应变值。
(5) 应变率效应是导致Taylor撞击尺寸效应的主要原因,Taylor杆尺寸越小,应变率越高,Taylor杆的动态屈服强度越高,无量纲塑性变形越小,造成小尺寸模型和大尺寸原型的结构响应不完全相似。
以上结论适用于Taylor杆低速撞击刚性靶、仅发生塑性变形情况下的尺寸效应问题。在高速撞击条件下,Taylor杆响应模式、能量转化机理发生了变化,对Taylor杆头部开裂、破碎的尺寸效应分析还需进一步研究。

