计及气体力的新能源涡旋压缩机型线齿头修正优化
冉志祥,何泽银,,向 银,,胡 欣,陶平安,胡立志
(1.重庆交通大学 机电与车辆工程学院,重庆 400074;2.重庆建设汽车系统股份有限公司 重庆市汽车热管理系统工程技术研究中心,重庆 400052)
0 引言
涡旋压缩机因其效率高、结构简单、运转平稳、微振低噪等特点,广泛应用于新能源汽车空调系统中。对于涡旋齿头的修正问题与修正引起的压缩机性能研究,国内外学者开展了大量有成效的研究工作。BRYCE 等[1]基于曲率半径推导了涡旋齿头修正方法,并利用修正参数计算了涡旋齿头体积。彭斌等[2-3]基于圆渐开线涡旋型线,建立了涡旋齿头双圆弧修正与双圆弧加直线修正两种修正优化模型,基于影响齿头修正的优化目标进行参数优化选取。吴昊等[4]针对双圆弧加直线修正后的汽车空调涡旋压缩机,提出了压缩腔特色计算方法,完善了对称双圆弧加直线修正理论。王君等[5]建立了圆弧修正几何模型,并基于中线设计方法,提出了多对圆弧修正方法,研究表明多对圆弧修正提高了压缩机工作性能。丁佳男等[6]研究了具有渐开线涡旋型线特征的变基圆渐开线型线方程,并给出了涡旋齿头双圆弧修正的型线方程,探究了修正展角对修正齿头形状的影响。唐景春等[7]基于变基圆涡旋型线,推导圆弧加直线修正方法,并计算齿头修正面积与内压缩比,研究了修正参数影响规律。张朋成等[8]提出了一种渐开线类变截面涡旋型线,分析了型线基本控制参数—压缩机性能影响规律,研究结果可为变截面涡旋压缩机性能研究提供理论依据。刘涛等[9]基于渐开线类组合型线,对3 段渐开线的组合形式进行优化设计,研究结果表明基圆渐开线类组合型线行程容积与面积利用系数最大。李超等[10-11]研究了涡旋压缩机热-气-固3 种载荷作用下的涡旋盘应力应变规律,并研究了气体力对压缩机转子系统造成的动不平衡问题,改进了压缩机结构,有效改善了轴承与机架受力,提高了压缩机运转稳定性。高艳等[12]基于气体力计算模型,分析影响气体力的压缩机相关参数,研究了各参数影响规律。
综上所述,国内外对于涡旋齿头的修正问题已经开展了大量的研究工作,但上述研究工作皆未涉及齿头修正对压缩机气体力的影响以及考虑气体力的修正参数优化。本文基于圆渐开线涡旋压缩机,建立涡旋齿头两种修正参数化模型,基于多目标遗传算法在考虑气体力下对修正参数进行优化选取,得到1 组参数有效解,对涡旋齿头修正参数的选取有一定的参考。
1 涡旋压缩机齿头修正方法
针对涡旋压缩机圆渐开线涡旋型线齿头过切,致使涡旋齿头形成尖点,涡旋压缩机余隙容积等工程问题,前人学者等提出涡旋齿头修正方法。涡旋齿头修正方法有许多,双圆弧加直线修正以良好的加工特性以及热力学性能等特点广泛应用于实际工程。
双圆弧加直线修正方法在双圆弧修正的基础上演化而来,双圆弧加直线修正相较于双圆弧修正多一修正参数——偏移量δ,其基本几何原理如图1 所示。图中,O,O1′,O2′ 为双圆弧修正中同等修正展角下的基圆、修正小圆弧、修正大圆弧圆心;O1,O2分别为双圆弧加直线修正的修正大圆弧、修正小圆弧圆心。双圆弧加直线的修正大、小圆弧圆心确定方法即在双圆弧修正的修正大、小圆弧圆心基础上沿渐开线发生线AC,BD 偏移修正偏移量δ。再用两圆弧的内切线连接两圆弧即得到双圆弧加直线修正全过程。图中E,F 分别为修正大、小圆弧内切线切点。
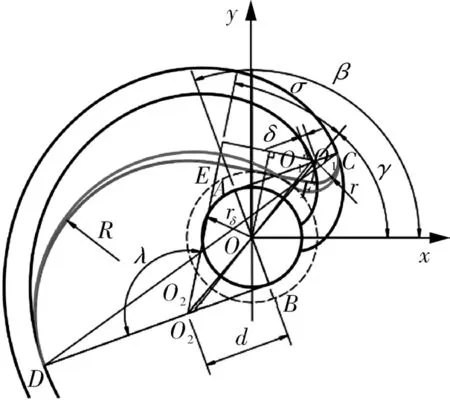
图1 双圆弧加直线修正几何原理Fig.1 Geometric schematic diagram of double arc plus straight line correction
其中,双圆弧加直线修正大、小圆弧圆心坐标如下:
式中,rb为基圆半径;γ为修正角;β为修正展角。
修正大、小圆弧内切点坐标解析如下:
式中,σ为异形三角形夹角。
由双圆弧加直线修正方法可知,其修正参数仅有2 个独立变量。双圆弧加直线修正参数间关系如下[13]:
式中,R 为修正大圆弧半径;r 为修正小圆弧半径;α为型线发生角;λ为修正圆弧圆心角。
2 涡旋压缩机齿头修正后性能计算
2.1 涡旋压缩机齿头修正面积
齿头修正面积即齿头修正后涡旋齿头轴向投影面积,其数值直接反映涡旋齿头强度,如图2所示。
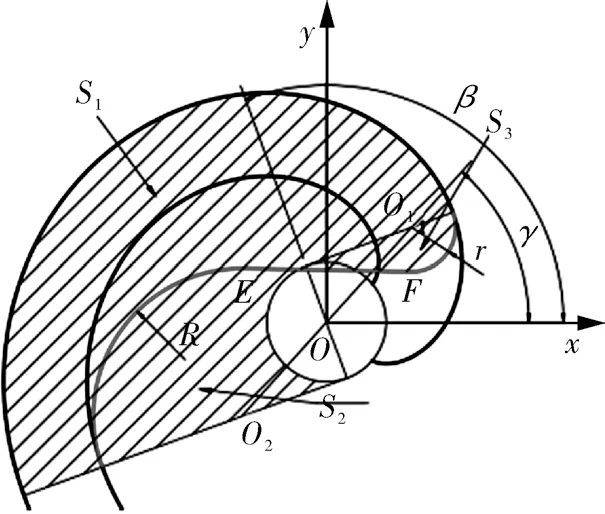
图2 修正面积示意Fig.2 Schematic diagram of corrected area
修正齿面积计算式为:
式中,SC为修正后涡旋齿头面积;S1为渐开线发生线扫过面积;S2为计算中多余面积;S3为齿尖面积。
齿头修正面积系数即修正前后齿头轴向投影面积相比,直接反映修正增加齿头面积比例。齿头修正面积系数计算式为:
2.2 涡旋压缩机齿头修正后气体力计算
涡旋压缩机气体力可分为:径向气体力、轴向气体力与切向气体力。涡旋齿头修正主要影响压缩机切向力与径向力。本文忽略轴向气体力的影响,主要考虑涡旋齿头修正对切向气体力与径向气体力的影响。
2.2.1 涡旋压缩机径向气体力
径向气体力是沿偏心轴径向方向施加在动、静涡盘上的气体作用力,方向平行于动、静涡旋盘基圆圆心连线,称为径向气体力,记为Fr,如图3所示。

图3 径向气体力示意Fig.3 Schematic diagram of radial gas force

图4 中心腔几何示意Fig.4 Geometric diagram of central cavity
当动、静涡旋盘之间具有N 对压缩腔时,径向气体力合力为[14-16]:
式中,Ps为吸气压力;h 为涡旋齿高;θm为修正侵入角;θ*为脱啮角;εi为各压缩腔压力比;Vs为行程容积;Vi为第i 个压缩腔容积。
2.2.2 涡旋压缩机切向气体力
切向气体力即沿偏心轴切线方向加在动、静涡旋盘上的气体作用力,记为Ft,其作用示意如图5 所示。
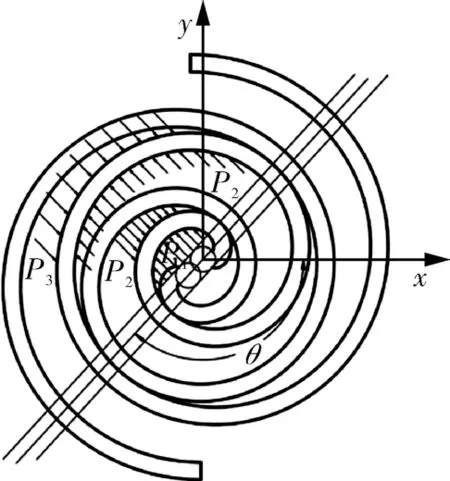
图5 切向气体力示意Fig.5 Schematic diagram of tangential gas force
切向气体力计算式为:
式中,Pt为节距。
2.3 涡旋齿头修正参数影响因素分析
2.3.1 涡旋齿头修正面积与系数
图6 示出了双圆弧加直线修正涡旋齿头修正面积与涡旋齿头修正面积系数随修正参数变化规律。
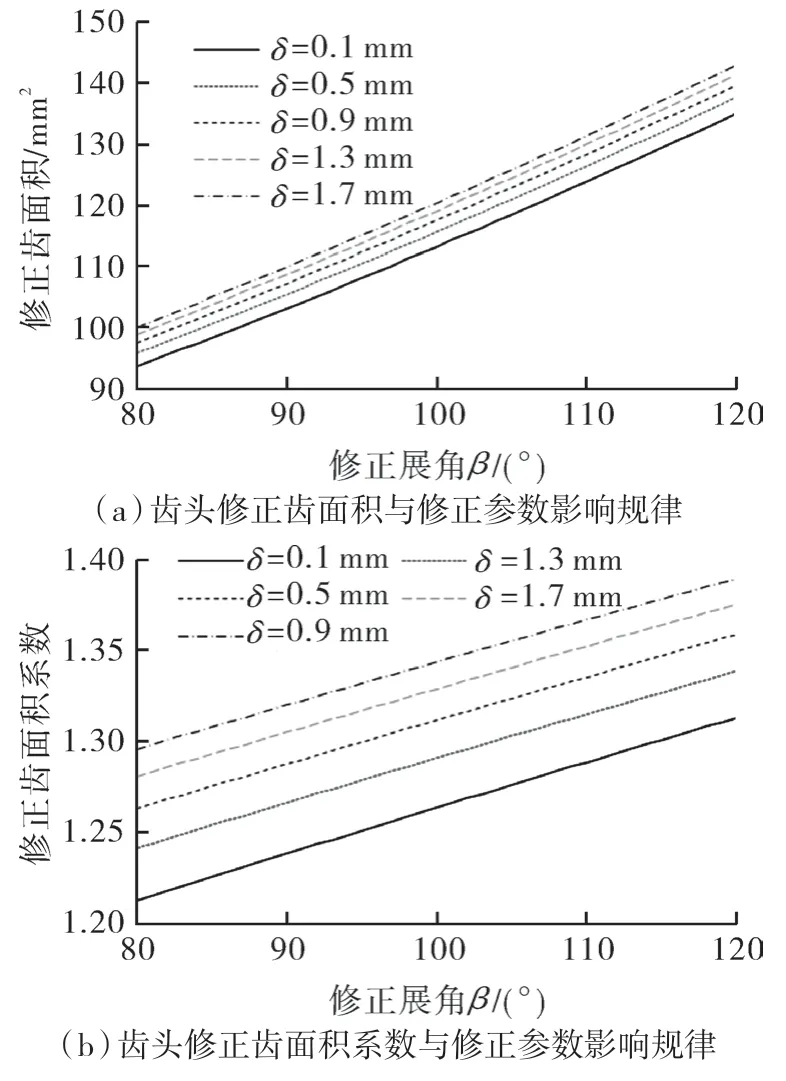
图6 双圆弧加直线修正参数影响规律Fig.6 Influence law of double arc plus straight line correction parameters
由图可知,随修正展角增加,双圆弧加直线修正的齿头修正面积与齿头修正面积系数皆呈增加趋势;在同一修正展角下,随修正偏移量增加,齿头修正面积与齿头修正面积系数也呈增加趋势。
2.3.2 涡旋压缩机径向、切向气体力
图7,8 分别示出了不同修正参数下径向气体力与切向气体力变化规律。
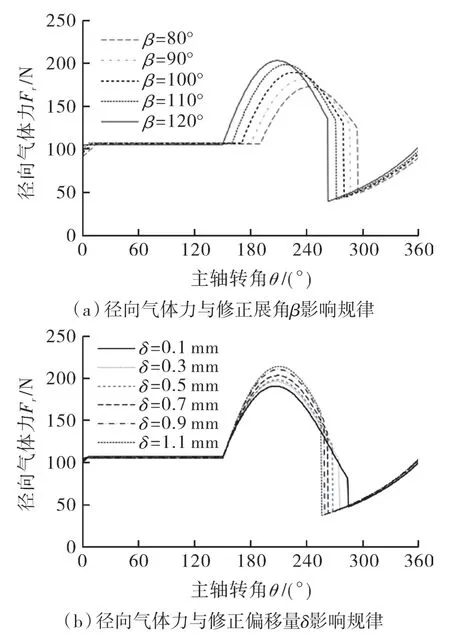
图7 径向气体力-修正参数变化规律Fig.7 radial gas force-change law of correction parameters
由图7 可知,对于径向气体力:随着修正展角增加,径向气体力峰峰值增加,图7(a)中修正展角120°时相较修正展角80°时径向气体力峰峰值增加31.5%;图7(b)中修正偏移量0.1 mm 时相较修正偏移量1.1 mm 时径向气体力峰峰值增加23.5%。
对于切向气体力:如图8 所示,随着修正展角自80°增至120°,切向气体力峰峰值增加15.2%;随着修正偏移量(0.1~1.1 mm)增加,切向气体力峰峰值增加7%。
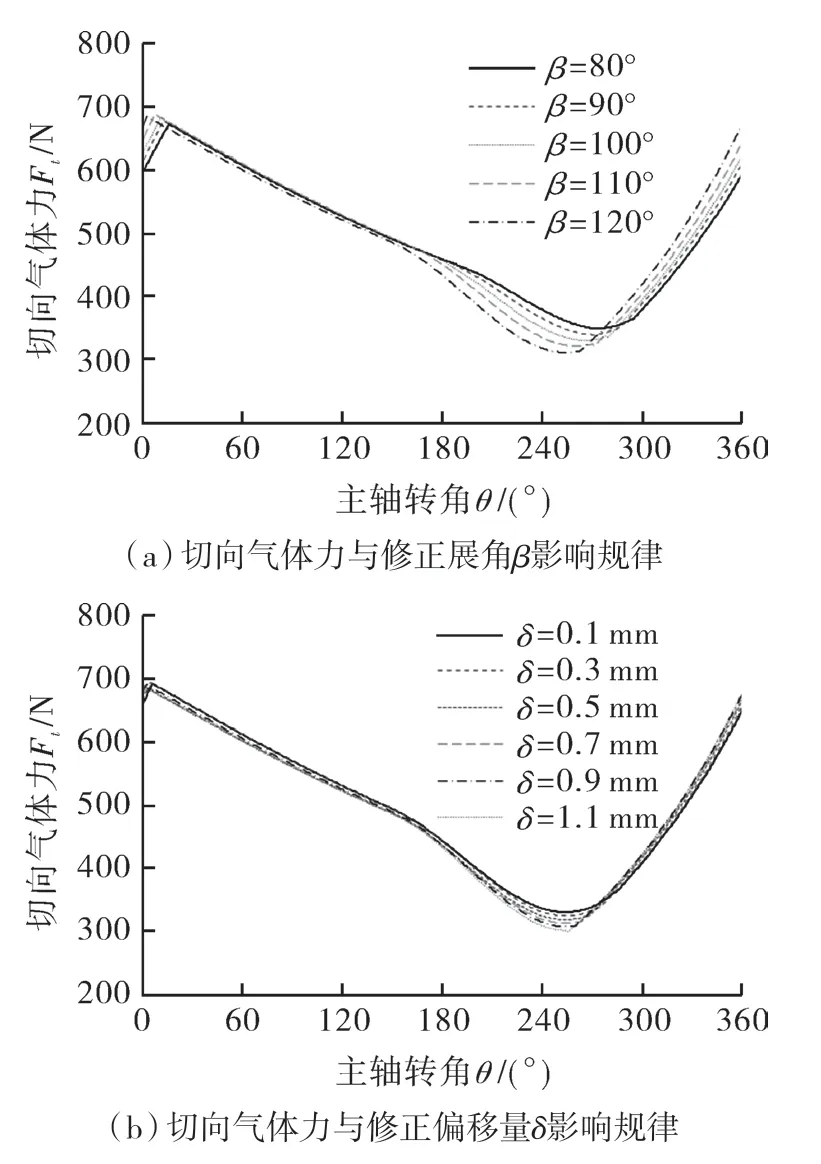
图8 切向气体力-修正参数变化规律Fig.8 tangential gas force-change law of correction parameters
综上所述,随着修正展角与修正偏移量增加,径向气体力与切向气体力峰峰值增大,气体力激烈程度增加,且径向气体力较切向气体力随着修正参数变化敏感。
3 涡旋压缩机涡旋齿头修正优化设计
遗传算法是基于仿生结构发展而来的智能算法,对于双圆弧加直线修正参数优化选取,其将修正方法中的修正参数视为“基因”,经过多代的繁衍、进化,进而产生较为优秀的子代,实现修正参数的优化选取。多目标遗传算法流程如图9所示。

图9 多目标遗传算法流程Fig.9 flow chart of multi-objective genetic algorithm
3.1 目标函数
切向气体力与径向气体力波动愈激烈,动、静涡旋齿间接触力愈加不平稳,致使涡旋齿间磨损加剧,降低压缩机寿命。因而气体力越加平稳,有利于提高压缩机可靠性;涡旋齿头修正面积与涡旋齿头强度正相关,涡旋齿头修正面积越大涡旋齿强度越大[17-19]。
整体优化目标函数采用最小值优化,将气体力峰峰值、涡旋齿头修正面积作为目标函数,即:
式中,f1(x)为径向气体力峰峰值;f2(x)为切向气体力峰峰值;f3(x)为涡旋齿头修正面积倒数。
3.2 自变量与约束条件
由上述齿头修正面积计算过程与气体力计算过程分析,确定了修正模型中的独立设计变量为:
考虑到实际的修正展角取值范围对修正参数取值范围取值为:
式中,r (β)为同等型线参数与修正展角下的修正小圆弧半径。
3.3 优化结果
计算气体力与齿头修正面积时需要涡旋压缩机基本结构参数,现针对某型号涡旋压缩机修正参数进行优化选取,其基本结构参数见表1。

表1 涡旋压缩机基本结构参数Tab.1 Basic structural parameters of scroll compressor
由修正参数影响规律可知,修正参数β,δ与气体力峰峰值、齿头修正面积呈正相关,
故目标函数中f3(x)与f1(x),f2(x)变化趋势相反,3 个优化目标无法同时取得极值,只能求得一组有效解。
运用MATLAB 进行优化算法进行求解,优化得到Pareto 解集的运行时间约为29 s。对3 个优化目标用多目标遗传算法进行参数优化选取,优化结果如图10 所示。某型号涡旋压缩机与求得最优值的对比结果见表2,其中方案1,2 都在齿头面积有增加的情况下降低了径向与切向气体力峰峰值,峰峰值降低最高达到22.6%,方案3 齿头面积降低了33%,但径向气体力峰峰值降低了46.9%。
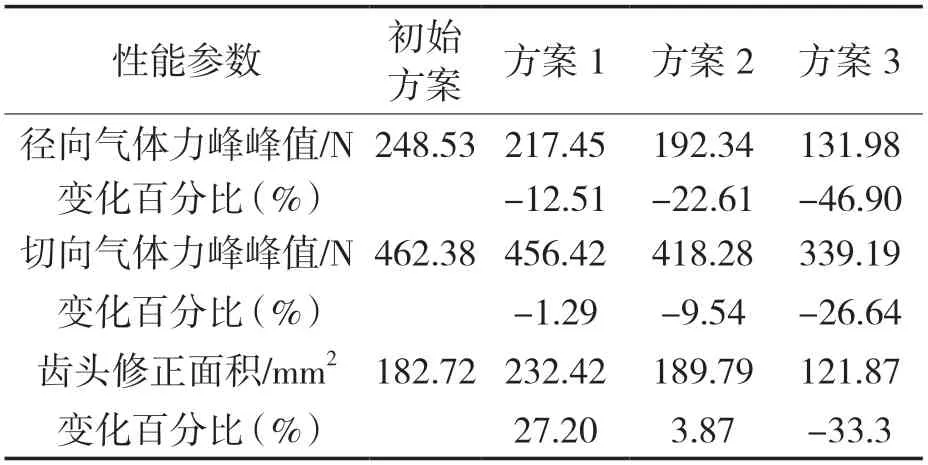
表2 修正参数优化结果对比Tab.2 Comparison of modified parameter optimization results

图10 双圆弧加直线修正参数优化结果Fig.10 Optimization results of double arc plus straight line correction parameters
3.4 结果验证
为验证计算结果准确性,基于涡旋盘实际参数进行三维建模,通过实际测量涡旋齿头修正面积与解析算法进行对比如图11 所示。

图11 齿头修正面积结果对比Fig.11 Comparison of tooth head correction area results
涡旋齿头修正面积结果对比见表3。

表3 涡旋齿头修正面积结果对比Tab.3 Comparison of corrected area results of scroll gear head
由图表可知,由修正参数进行实际三维建模测量涡旋齿头投影面积与解析算法计算结果对比,涡旋齿头解析算法结果具有正确性。
4 结论
(1)解析了双圆弧加直线修正后的涡旋齿面积与径向、切向气体作用力,并分析了修正模型下的修正参数影响规律。
(2)基于涡旋齿头面积与径向气体力计算方法,采用多目标遗传算法,对双圆弧修正方法的修正参数进行优化选取,得到了1 组有效解;对比实际某型号涡旋压缩机参数,在涡旋齿头面积增加情况下,气体力峰峰值最大降低22.61%,验证了优化结果的有效性。
(3)基于涡旋齿优化后修正参数,进行三维建模测量涡旋齿头面积,与解析计算结果进行对比,结果吻合良好,验证了解析算法正确性。

