基于分层误差补偿的飞机柔性工装定位精度提高方法

刘振宇,喻明让,陈 云,郗唯杰

(1.中北大学航空宇航学院,山西 太原 030051)

(2.北方自动控制技术研究所,山西 太原 030006)

飞机大部件装配技术逐步从传统的模线样板技术向数字化、柔性化方向发展,是现代航空工业的重要组成部分[1]。为了提高装配的效率和定位精度,许多学者对柔性装配工装进行了研究。郭飞燕等[2]对数控定位器进行了误差建模,实现装配孔的高精度定位;朱永国[3]对大部件装配中的若干关键技术进行了研究,构建了飞机翼身装配系统;郭志敏等[4]分析了导轨基准面的定向公差,为工装设计提供了依据;李晨等[5]分析了装配工装的具体结构和工作流程;陈伟东[6]采用力位混合控制的方法对大型飞机翼身装配过程中的变形量进行修正,提高最终的装配精度;Reid[7]设计了AGV小车和柔性工装共同调姿的装配方法,提高了装配的灵活性和效率;刘继红等[8]基于装配中的关键特征进行位姿拟合,提高了对接的精度;刘华[9]通过视觉定位技术提高了飞机的装配精度和系统的伺服性能。

建立定位器的误差补偿模型是装配过程中重要的一环,然而上述研究中并未考虑导轨之间的关系,仅对其线性误差进行了补偿,未考虑其非线性误差带来的影响。本文基于改进的线性误差补偿模型与遗传BP神经网络构造分层误差补偿模型,以提高装配过程中的定位精度和装配效率。

1 基于导轨相关的定位器误差模型改进

目前,定位器采用的是X、Y、Z三层堆栈式结构,主要对其安装定向误差、滚珠丝杠导程误差和轴向进给误差进行补偿,但没有考虑定位器层与层之间安装角度的相互影响,因此可通过分析导轨的相关性来提高其模型的定位精度。以最上层Z导轨为例:

αzz=εz(z)+εz(x)+εz(y)

(1)

βzy=εy(z)+εy(x)+εy(y)

(2)

γzx=εx(z)+εx(x)+εx(y)

(3)

式中:αzz、βzy和γzx分别为Z导轨滚转角、俯仰角和偏转角;εi(i)为对应导轨沿相应轴的角度误差,i=x、y、z。

将考虑了导轨堆栈式结构的安装角度误差代入文献[2]中的误差补偿公式,可得到定位器整体空间误差补偿值ΔE:

(4)

式中:ΔXP、ΔYP和ΔZP为对应导轨方向的误差值。

采用上述改进后的模型对定位器进行第一次整体线性误差补偿,但实际生产中还有一些误差无法线性化,无法用上述模型对其进行补偿,故采用神经网络法进行第二次补偿。

2 遗传算法优化BP神经网络处理非线性误差

2.1 非线性误差的分析与处理

柔性装配中存在的非线性误差如热误差、大部件变形误差和伺服系统爬行振荡误差等会对定位器的定位精度产生影响[10]。传统的处理非线性误差的方法多为建立单一因素的误差模型,但因其复杂性导致无法同时对多种非线性误差进行补偿,故补偿效果不理想且通用性较差。也有学者用神经网络处理系统的非线性误差,但由于神经网络固有的缺点[11],如学习速度慢、容易陷入局部极小值和网络推广能力有限等问题,因此误差补偿效果也不理想。基于上述原因,本文采用遗传算法优化的BP神经网络(GA-BP)解决这一问题,使其更好地与改进的误差模型结合,提高系统的定位精度。

2.2 遗传算法优化BP神经网络

BP神经网络具有很强的非线性映射能力和柔性网络结构,用遗传算法对其进行优化能得到更好的预测结果。在BP神经网络训练的过程中,第一次向前传播的权重和阈值采用随机方法确定,这也是导致其容易陷入局部最小的主要原因。因遗传算法有很好的全局搜索能力,故引入其对权重wij和阈值bij进行编码,通过选择、交叉和变异得到最优的初始权重和阈值,然后进行训练以避免陷入局部极小,达到提高模型精度的目的,流程如图1所示。

图1 遗传算法优化BP神经网络流程

Step1,对输入的数据进行预处理,并生成相应的BP神经网络结构。

Step2,种群初始化,用遗传算法对网络初始值进行编码,编码内容由输入层与隐含层连接权值、隐含层阈值、隐含层与输出层连接权值以及输出层阈值4部分组成。

Step3,设置适应度函数并计算,把网络的输出值与真实值之间的误差绝对值作为个体适应度值F,计算公式为:

(5)

式中:n为网络输出节点数,yi和oi分别为网络第i个节点的输出值和真实值。

Step4,按适应度值F和遗传算法选择、交叉、变异的结果对个体进行筛选,保留适应度值较高的个体,反复循环直到终止条件为止。

Step5,将得到的最优权值、阈值用作网络的初始值,进行误差补偿的相关计算。

3 分层误差补偿模型

为了更好地将线性误差补偿与非线性误差补偿结合起来,本文提出了分层误差补偿模型用来提高柔性工装的定位精度。该模型的原理是:将补偿过程分为两层,即线性补偿和非线性补偿,先通过导轨相关性改进的模型进行线性补偿,计算出补偿后各样本点与理论值的偏差并筛选出偏差较大的点,然后用这些样本点对GA-BP进行训练,再对系统进行非线性补偿,具体步骤如图2所示。

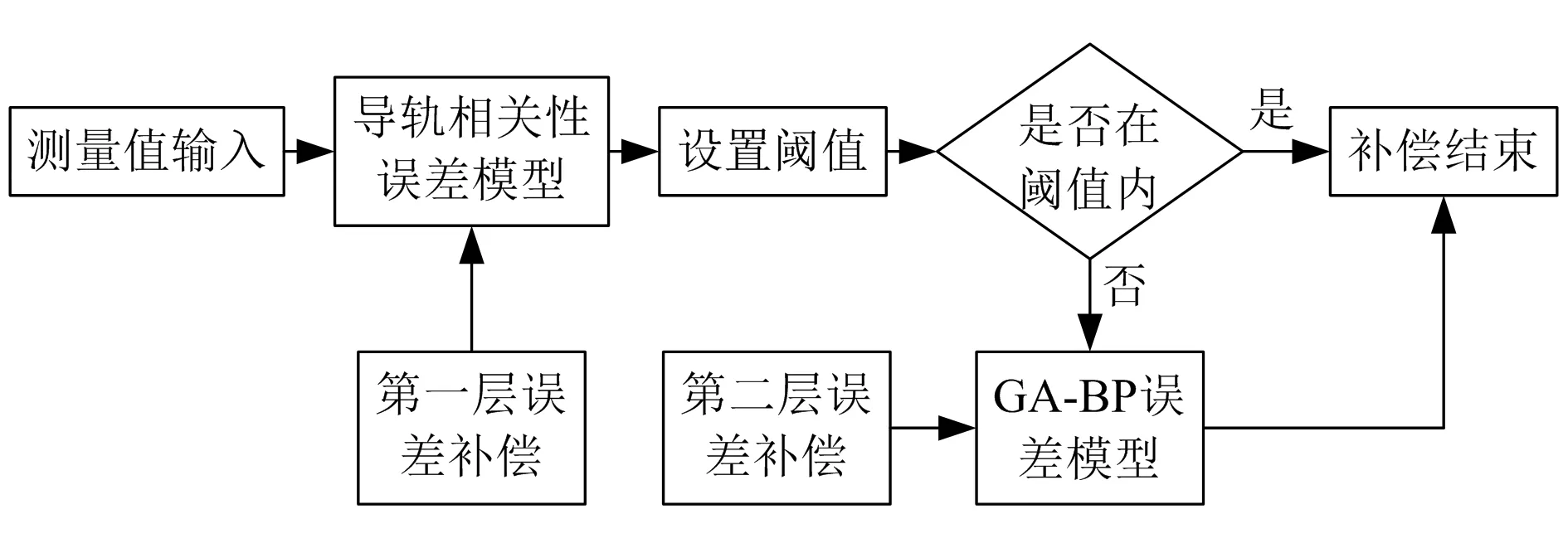
图2 分层误差补偿模型

输入的测量值经过分层误差补偿模型第一层补偿之后,工装系统整体定位精度提高且由安装定向等引起的误差得到了补偿,其中造成部分样本点偏差较大的主要原因为热误差和部件变形等非线性误差,故采用GA-BP对其进行第二层误差补偿,进一步提高工装系统的定位精度。

4 实验验证

本文设计了相应的实验验证了分层误差补偿模型的正确性和高效性。采用大部件柔性装配平台、莱卡AT403激光跟踪仪和自动调姿系统搭建实验平台,如图3、图4所示,通过比较传统误差模型与分层误差模型的补偿效果,来说明分层误差补偿模型更加准确。

图3 大部件柔性装配平台

图4 测量实验平台

对实验平台进行整体坐标系构建,将靶球固定于定位器标杆处并驱动定位器沿三个方向运动,取2 mm为测量间距,分别重复进行三次实验,取测量均值记录于表1～4。

表1 X轴方向测量值 单位:mm

表2 Y轴方向测量值 单位:mm

表3 Z轴方向测量值 单位:mm

表4 空间测量值 单位:mm

分别用传统误差模型与分层误差模型对测量数据进行误差补偿,定位器各方向误差和空间误差的分析结果如图5～图8所示,将两种补偿结果的最大值和均值记录于表5。

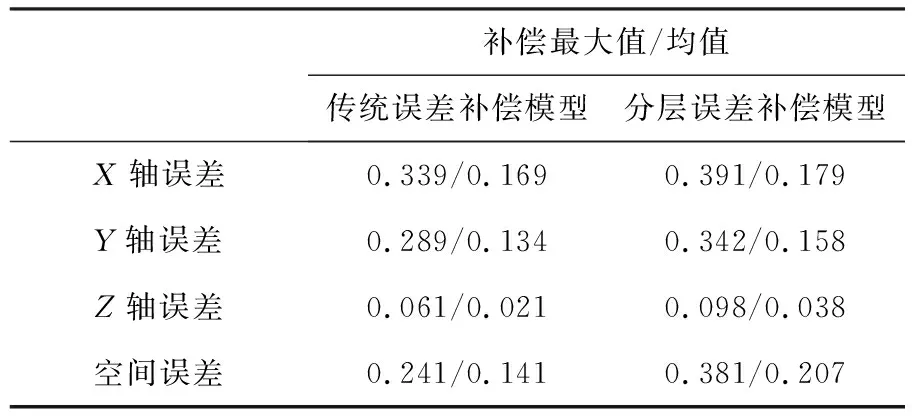
表5 补偿后最大补偿值和补偿均值 单位:mm

图5 X轴误差值

图6 Y轴误差值

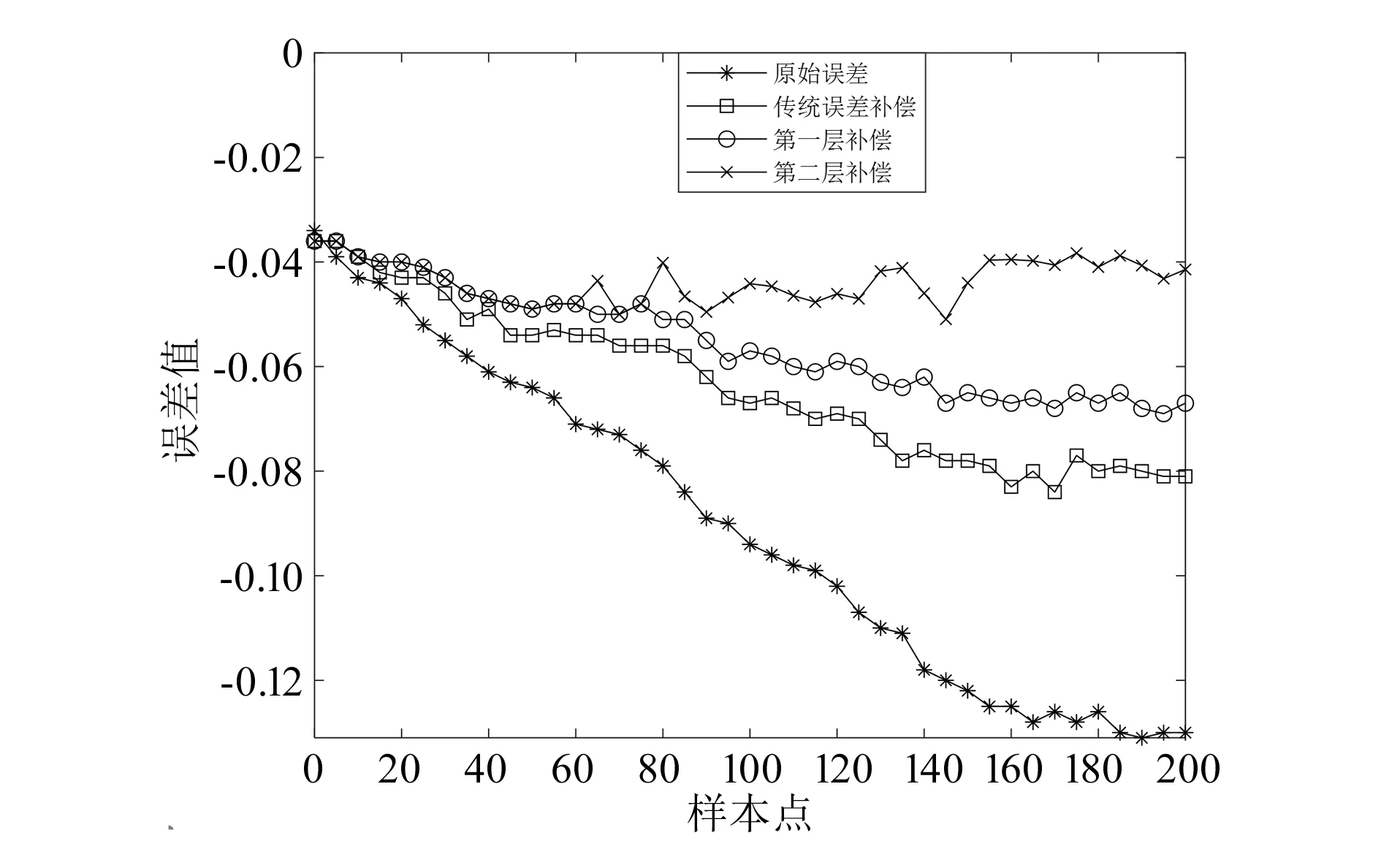
图7 Z轴误差值

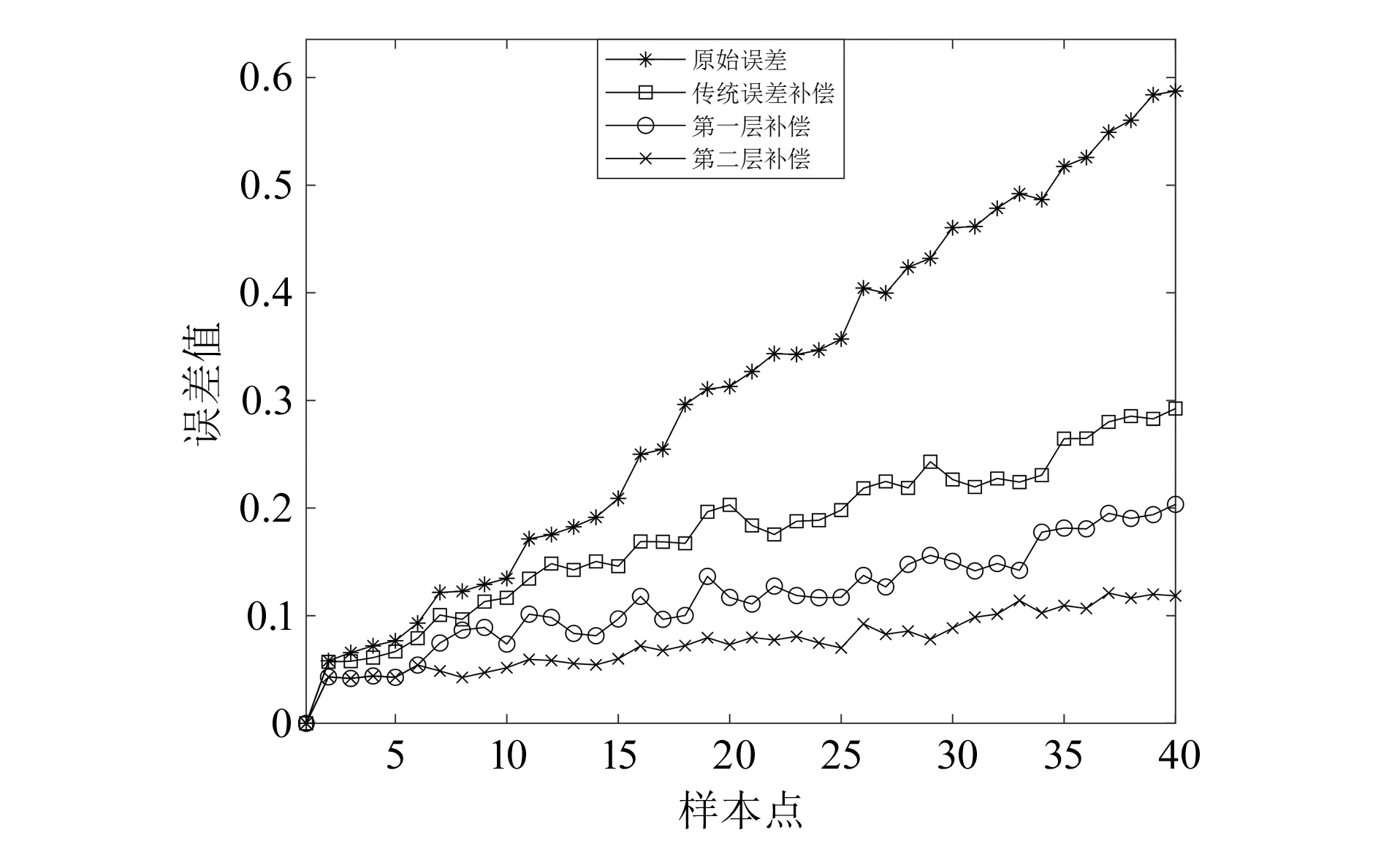
图8 空间误差值

由图5～图8和表5可以看出,定位器经分层误差补偿模型修正后,误差总体呈下降趋势,与传统误差补偿模型相比更接近理论值,X、Y和Z轴分层补偿效果与传统补偿效果相比最大值分别提高了15.35%、18.37%和46.44%,均值分别提高了6.17%、17.97%和41.21%,空间误差分层补偿效果与传统补偿效果相比最大值可提高58.09%,均值可提高46.92%,证明了分层误差补偿模型的正确性和高效性,有更好的补偿效果,更符合工程实际。

5 结束语

本文对飞机柔性工装中三坐标定位器的误差模型进行了分析,基于导轨相关性对传统误差补偿模型进行了改进,建立了定位器空间误差补偿公式,与传统的单一导轨建模相比提高了线性补偿精度,通过遗传算法优化的BP神经网络对定位器的非线性误差进行补偿,并将线性模型和非线性模型相结合,提出了分层误差补偿模型,有效地提高了定位器的定位精度,为后续基于协调孔装配提供了技术保障。但本文仅对单个定位器进行了误差补偿,后续将基于各定位器之间的并联关系对柔性工装整体进行建模分析,在提高测量数据准确性的基础上建立装配系统的误差补偿模型。热变形等非线性误差受装配环境实时影响,故如何建立更准确的误差模型仍需进一步研究。