砂卵石层盾构开挖面失稳分析及双参数掘进控制
姚琦钰, 张润来, 宫全美, 周顺华
(1. 同济大学 道路与交通工程教育部重点实验室,上海 201804;2. 同济大学 上海市轨道交通结构耐久与系统安全重点实验室,上海 201804)
砂卵石层较为松散,无黏聚力,卵石颗粒间点对点接触形成颗粒拱[1]。颗粒自身性质和颗粒间相互作用影响了散粒系统的宏观力学行为[2-3],使该类地层受到盾构施工扰动后不稳定,易产生超挖并出现开挖面失稳,甚至发展至地表形成突发性坍塌[4-5],造成生命财产损失。
保证开挖面稳定性的关键在于提供合理的开挖面支护力,国内外学者为确定开挖面失稳破坏模式和极限支护压力已开展了一系列研究。周顺华等[6]分析了开挖面空间效应区的位移释放,建立了应力释放与位移释放间的关系。Kamata和Mashimo[7]采用块状二维离散元(DEM)颗粒流程序进行开挖面稳定性模拟,认为开挖面处的颗粒剥落是开挖面失稳的标志,并简单揭示了开挖面失稳过程和机理。缪林昌等[8]、孙潇昊等[9]使用二维PFC模拟砂土层中的盾构施工过程,得到土体不同的密实程度情况下开挖面稳定性、失稳破坏形态和极限支护力。Chambon和Corte[10]采用模型试验对砂性土中隧道开挖面稳定性和失稳破坏发展机理进行研究,对于不同密度砂层、隧道埋深,给出了开挖面支护力控制值。李守巨等[11]、Yu等[12]基于土仓渣土质量守恒,提出了盾构掘进和静止状态时的土仓压力计算模型。王明年等[13]采用三维颗粒流程序(PFC)研究了成都砂卵石地层地铁盾构隧道开挖面稳定性,将开挖面失稳划分为三个阶段,并指出极限支护应力比(极限支护应力与侧向静止土压力的比值)低于0.1时开始失稳。Chen等[14]针对砂土层盾构隧道的开挖面稳定性开展了三维PFC离散元分析,得到了不同埋深条件下的极限支护力大小以及失稳区范围。孙玉永等[15]结合盾构穿越既有隧道的施工案例,采用数值模拟方法分析了不同埋深的既有隧道下方土压力分布规律,分3个区域给出了土仓压力的设定公式。
也有学者基于盾构施工实例分析对盾构土仓压力设定和其他掘进参数设置进行研究。Ercelebi等[16]、Chakeri 等[17]分别依托土耳其伊斯坦布尔穿越砂层的双线地铁盾构隧道工程和朗德黑兰穿越软土、卵石土等复杂地层的地铁7号线工程,讨论了隧道埋深、隧道尺寸、掌子面压力等因素对开挖面上方地表沉降的影响,指出掘进时应实时调整土仓压力以减小地表沉降。杨旸等[18]分析了南宁圆砾层盾构掘进参数,提出应采用Terzaghi 松动土压力和静止土压力计算值作为土仓压力的取值范围。Yao等[19]基于兰州砂卵石层盾构刀盘卡死案例的施工实测数据分析,提出了盾构刀盘卡死后的脱困方法和控制指标。Zhao等[20]基于机械与岩土相互作用和机械性能配置对盾构机在复合地层中掘进参数进行分析,建立了复合地层中刀盘总扭矩理论计算模型,提出了适用于不同机械配置、地层条件的盾构掘进贯入度预测方法。王春凯[21]采用数理统计对砂卵石地层中土压平衡盾构施工实测参数进行分析,建立了推进速度与刀盘扭矩的数学模型,提出盾构土仓压力与推进速度呈线性正相关,刀盘扭矩与总推力、刀盘转速、土仓压力之间的关系近似呈二次抛物线形式。上述研究中采用的开挖面形态与真实形态仍存在差异,且现有研究对工程案例数据的分析以回归分析建立经验模型为主,多针对单一参数,未能考虑盾构机整体机械性能配置。
本文基于成都地铁某盾构区间的开挖面失稳案例,开展了三维离散元数值模拟,对不同支护力分布形式的开挖面失稳过程和土压力变化规律进行了分析,并结合盾构超挖区段的实测数据和盾构机整体机械性能配置,对盾构超挖成因和开挖面稳定性控制进行了研究,从土仓压力和刀盘转速设置两个方面提出了控制措施。
1 土压平衡盾构开挖面失稳实例
成都地铁某盾构区间全长860 m,隧道主要穿越地层为卵石土层,水位埋深5.6~8.0 m,盾构施工采用海瑞克复合式盾构机,区间地质纵断面及盾构刀盘结构如图1 所示。砂卵石点荷载试验强度为55.7~132.9 MPa,地层中伴有漂石,质量含量为5~20 %,区间隧道穿越地层的物理力学参数如表1所示。

表1 土层物理力学参数Tab. 1 Physical and mechanical parameters of soil layers

图1 盾构区间地质剖面图及盾构刀盘结构Fig. 1 Geological profile of shield section and photo of shield cutter head
该地层具有卵石含量高、黏聚力低、离散性强的特点,导致施工过程中土仓压力控制困难,盾构机在该区间施工时频繁发生超挖现象。盾构掘进过程中对开挖面出土量进行了称重记录,由于出土量的称重记录会受到当前掘进环的渣土改良剂重量影响,同时为统一考虑掘进过程中的1.2 m 转弯环和1.5 m通用环,采用每延米出土净重W进行分析,即减去渣土改良剂重量后的每延米出土重量,如式(1)所示。本文定义超挖系数α0以衡量超挖水平,如式(2)所示。
式中:Wa为每环渣土实际称重;ρg为注入渣土改良剂的密度;Vg为注入渣土改良剂的体积;L为每环实际掘进距离;Wt为每延米理论出渣重量。
图2 为盾构掘进前220 环范围内的每环超挖系数统计图,该区段内的超挖系数最高超过了0.6,最终造成地表坍塌。
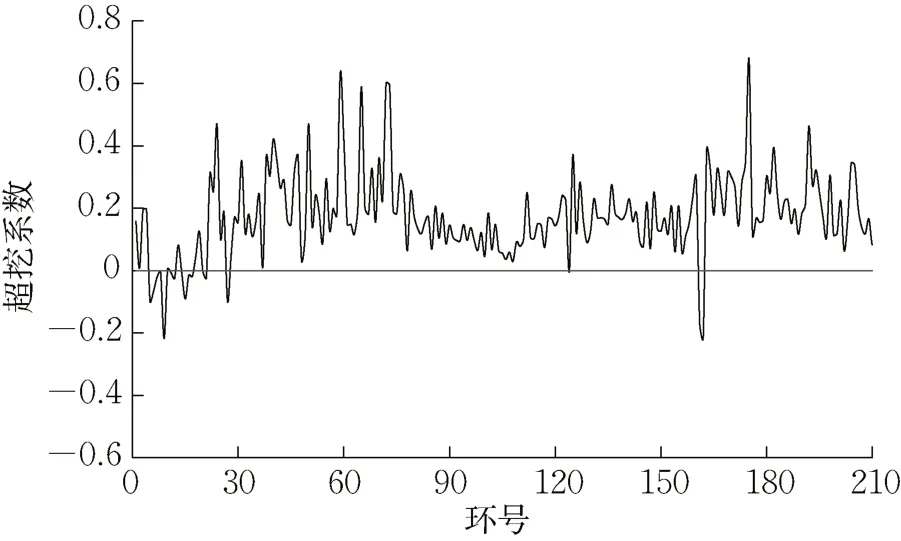
图2 盾构掘进前220环范围超挖系数Fig. 2 Over-excavation coefficient of shield tunneling from ring 0 to ring 220
2 土压平衡盾构开挖面稳定性离散元模拟
为探究在支护力真实分布形态下的土压平衡盾构开挖面稳定性,本文采用EDEM(engineering discrete element method)离散元数值软件,分析了开挖面极限支护力和开挖面失稳过程中的土压力变化规律。
2.1 颗粒参数标定
对于第1 节所述砂卵石层盾构施工案例,散体颗粒间无黏聚力,在EDEM 中采用Hertz-Mindlin 接触刚度模型,其中的本征参数通过地质勘测确定,接触参数通过虚拟实验确定,本文采用堆积角试验标定接触参数,再通过三轴数值试验对标定后的模型宏观力学特性与真实地层的匹配性进行验证。
2.1.1 颗粒制备
本文案例中隧道断面穿越的<2-9-3>与<3-8-3>两层卵石地层粒径分布十分相近,选取<3-8-3>密实卵石土进行标定。为节约计算资源将实际地层中较小粒径的颗粒进行等质量替代,对粒径超过400 mm但含量较小的颗粒也并入到400 mm的粒径中,质量等效替换后的颗粒粒径分布如表2所示。

表2 EDEM模型中不同颗径的颗粒含量表Tab. 2 Content of particles with different diameters in EDEM model
2.1.2 堆积测试
通过虚拟堆积测试来确定土体的自然休止角,使用墙体单元围成一个立方空间并在内部生成颗粒,打开侧向挡板,颗粒在重力作用下滑落直到自然静止,记录颗粒斜面与立方空间底面的夹角。颗粒的本征参数取值如表3 所示,接触参数按照碰撞恢复系数0.2~0.4(每组间隔0.1),静摩擦系数0.4~0.7(每组间隔0.1),滚动摩擦系数0.05~0.2 范围内设定(每组间隔0.05),颗粒与墙体的接触参数设置与颗粒间相同,共计48 组。经过结果对比,选取与地勘实测休止角(32°)误差最低的一组接触参数(误差为1.9%),即碰撞恢复系数、静摩擦系数和滑动摩擦系数分别为0.3、0.6和0.1。
2.1.3 三轴试验
基于堆积试验确定的接触参数开展虚拟三轴试验,三轴试验尺寸为150 cm × 300 cm,填充试样颗粒后通过上下钢板进行加载,在试样轴向应变达到15 %时停止试验。图3为围压在200、400和600 kPa下的三轴试验应力应变曲线,根据试验结果绘制强度包络线并可计算得到试样的摩擦角为33.8°,与真实地质参数接近,说明通过堆积试验标定的颗粒参数能反映地层的宏观强度特性。
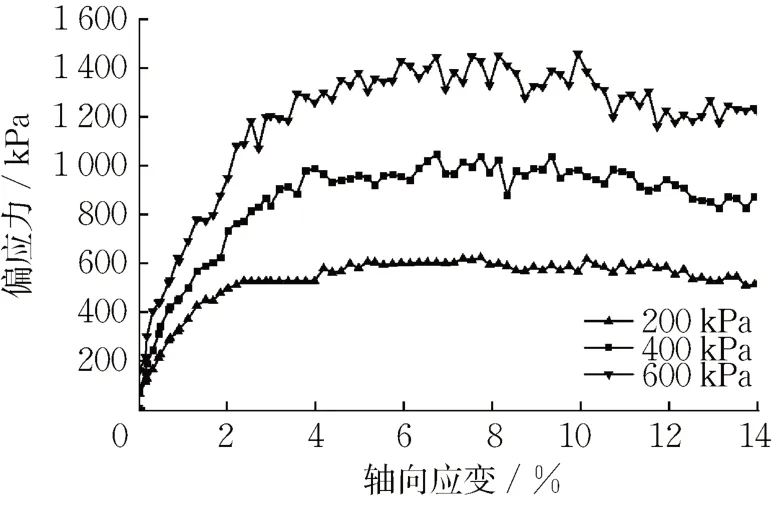
图3 虚拟三轴试验结果Fig. 3 Results of triaxial test in EDEM
2.2 盾构开挖面稳定性分析离散元模型
为开展盾构开挖面稳定分析,对盾构刀盘结构、土仓和周围地层进行数值建模,采用墙体单元模拟盾构机圆柱形外壳以围成土仓侧面。本文针对的砂卵石层盾构隧道直径在6 m 左右,对地层卵石进行质量等效替换后的颗粒平均粒径为20 cm,综合考虑模型规模和计算速度,将模型尺寸缩小3倍,重力加速度采用3 g。建立了2倍埋深条件下的三维离散元开挖面分析模型如图4 所示,模型尺寸为4 m×6 m×7 m,盾构直径为2 m,盾构从边界向土体中插入1 m,距离下边界1 m,并根据颗粒所处深度的不同设定了6层灰度层以便观察地层变形。

图4 2倍埋深条件下的三维模型及纵断面图Fig. 4 Three-dimensional model and profile view at double burial depth
盾构开挖面采用应力控制法模拟,将水平向的体力施加在开挖面边界颗粒上,在开挖面的上方、顶部和中部分别标识A、B、C 共3 个颗粒,在逐渐减小支护力的同时记录3个标识颗粒的位移变化。
2.3 盾构开挖面稳定性计算结果分析
2.3.1 支护力分布对极限支护力的影响
采用梯形支护和均匀支护两种开挖面支护力形式,其中梯形支护根据土仓渣土自重设置梯度,均匀支护为平均支护应力,两种支护力分布形式如图5所示。
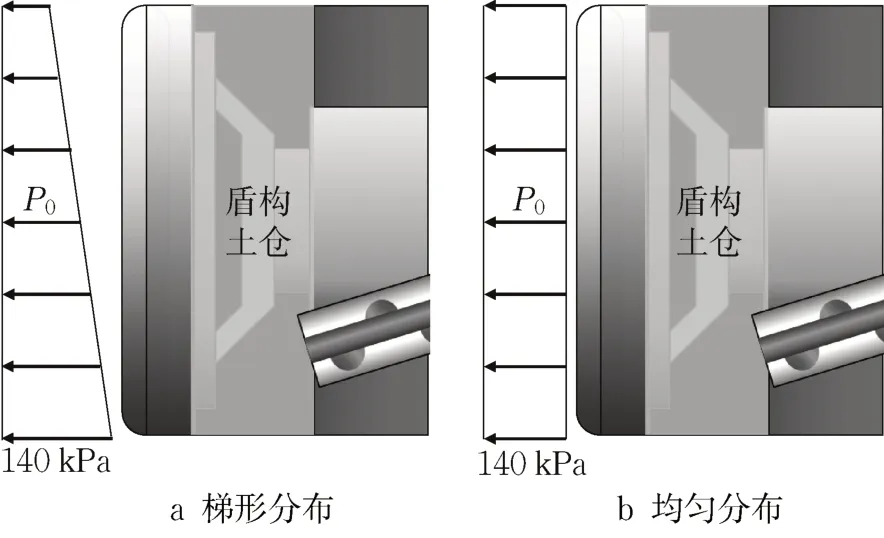
图5 2种开挖面支护力分布形式Fig. 5 Two types of support force distribution on excavation face
图6展示了开挖面在梯形支护条件下标识颗粒的位移变化。在支护力降低的初期,标识颗粒位移较小,当支护力下降至0.24P0时,开挖面向隧道内部方向变形较大,少量颗粒出现脱离,支护力下降至0.22P0时,颗粒B处已发生局部失稳,部分颗粒涌出开挖面,支护力下降至0.2P0时,开挖面发生失稳,此时颗粒B 已从开挖面脱落且颗粒将继续发生流动。因此,支护力为0.2P0时可认为开挖面已经整体失稳。

图6 梯形支护条件下开挖面颗粒的位移变化Fig. 6 Displacement of particles in excavation face under trapezoidal support force condition
图7为开挖面在均匀支护条件下标识颗粒位移变化情况。当支护力下降至0.2P0时,开挖面上的少量颗粒开始穿过应力边界并脱落,支护力下降至0.17P0时,颗粒C处开挖面变形较大,已接近临界状态,部分颗粒涌出开挖面,当支护力下降至0.15P0时,开挖面发生失稳,大量颗粒涌入盾构内,此时颗粒C 已从开挖面脱离。因此,支护力为0.15P0时可认为开挖面已经整体失稳。

图7 均匀支护条件下开挖面颗粒的位移变化Fig. 7 Displacement of particles in excavation face under uniform support force condition
综上可得,随着支护力降低,采用梯形分布支护时,开挖面顶部最先发生失稳,采用均匀支护时,开挖面中心处最先发生失稳。作用相同大小的支护力时两个颗粒在梯形支护形式下的位移比均匀支护方式的位移更大,且梯形支护形式所需的极限支护力比均匀支护形式更大。
2.3.2 开挖面失稳分析
由2.3.1 节中的分析可知采用梯形支护形式更加保守,且与盾构土仓内的支护力分布更加接近,因此后续计算采用梯形分布的支护形式。开挖面失稳后周围地层发生失稳流动,为了确定发生流动的地层边界,采用stream型颗粒以记录颗粒的位移过程,其流线长度表示颗粒位移量值,可以跟踪失稳后产生位移的土体范围,得到失稳区边界。在2倍埋深、支护力为0.2P0条件下颗粒发生位移的范围如图8a所示,可以看出发生位移的区域为椭球体,隧道上方的失稳区高度为1.5 D(D 为隧道直径),宽度为1.2 D,失稳区域并未发展至地表,支护力为0.1 P0时颗粒产生位移的范围如图8b所示,隧道上方的失稳区域宽度仍为1.2 D,但在竖向方向已发展至地表。
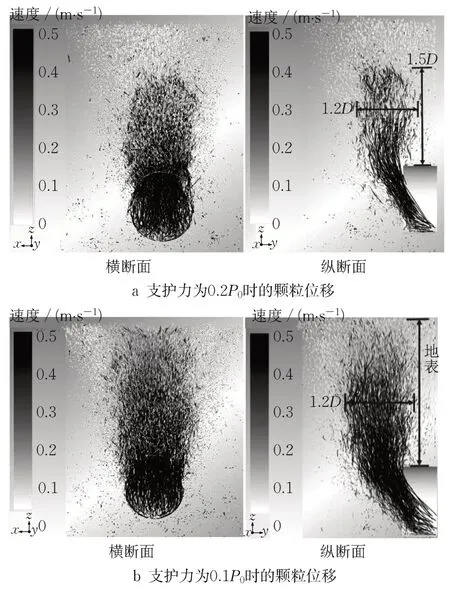
图8 2倍埋深条件下支护力不足时的颗粒位移Fig. 8 Particle displacements at double burial depth with insufficient support force
2.3.3 土压力变化规律分析
开挖面处颗粒在初始静止状态(支护力为P0)、临界支护状态(支护力为Pf)和失稳状态(支护力为0.2P0)下开挖面前方的竖向土压力和侧土压力如图9 所示。临界支护状态时,盾构上方0.75 D 范围内竖向土压力迅速减小,这是由于产生了土拱效应,竖向荷载通过土体抗剪切作用传递至周围土体。当支护力继续降低到0.2 P0后,土拱区域向上发展到1.25 D 范围。侧土压力在土拱区域顶部增大,在土拱区域内部减小。通过竖向应力和侧土压力计算得到的侧土压力系数如图10 所示,在临界支护状态时,侧土压力系数在土拱区域达到最大值0.73,当支护力下降至0.2 P0后,侧土压力系数的峰值位置随着失稳区域的向上发展而上移,最大值降至0.65。

图9 不同支护力条件下的竖向土压力与侧土压力Fig. 9 Vertical pressure and lateral pressure under different support force conditions

图10 不同支护力条件下的侧土压力系数Fig. 10 Coefficient of lateral earth pressure under different support force conditions
3 超挖分析与盾构掘进双参数控制
根据本文第2 节中的离散元分析可知,开挖面失稳、超挖与盾构土仓压力产生的支护作用直接相关。本节进一步分析了超挖系数与土仓压力和刀盘扭矩间的关系,并对盾构掘进时通过主动控制土仓压力和刀盘转速维持开挖面稳定的方法展开分析,提出了针对砂卵石地层6 m级土压平衡盾构掘进的双参数控制建议值。
3.1 土仓压力控制
统计本文第1 节中案例区间中10~220 环1#土仓压力数据,将土仓压力每隔5 kPa 划分一个区段,并将各土仓压力区段中的超挖系数取平均值以表征该区段的超挖系数大小,两者之间的关系如图11所示。土仓压力设定在25~75 kPa 时,开挖面超挖系数与土仓压力值成反比关系,提高土仓压力能够有效降低超挖系数。但当土仓压力设定在75~110 kPa 时,土仓压力的提高并不能有效防止开挖面超挖,超挖系数反而有所增加。
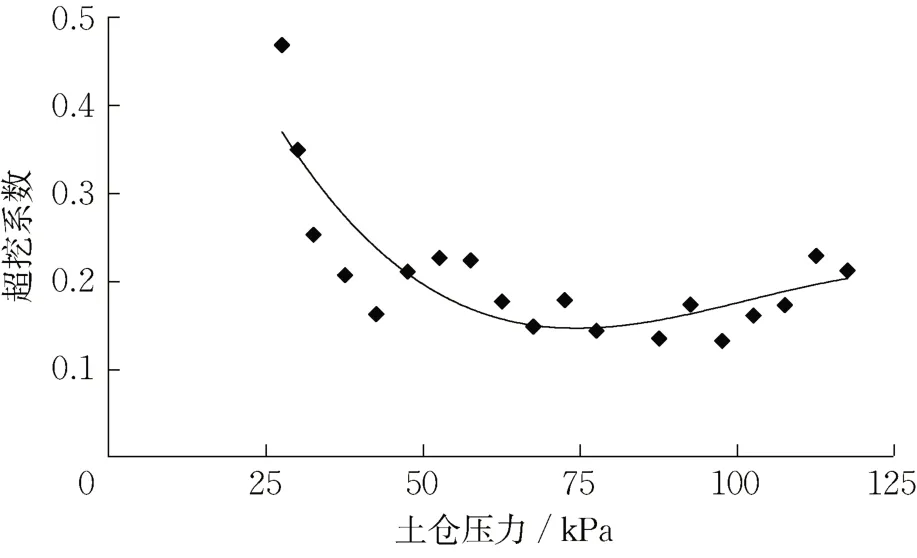
图11 超挖系数与平均土仓压力的关系Fig.11 Over-excavation coefficient versus average chamber pressure
对土仓压力较大时发生的超挖系数上升现象开展进一步分析,发现土仓压力设定较高的施工环数刀盘扭矩较高,易发生刀盘卡死,土仓压力提高至75 kPa 以后,继续提高土仓压力对控制超挖不再有效。将刀盘扭矩每隔0.5 MN·m 划分一个区段,并将各刀盘扭矩区段中的超挖系数取平均值,获得两者间的关系如图12 所示。超挖系数与刀盘扭矩存在正向相关性,扭矩较大说明掘进较为困难,刀盘卡死几率增加,也更易发生超挖。
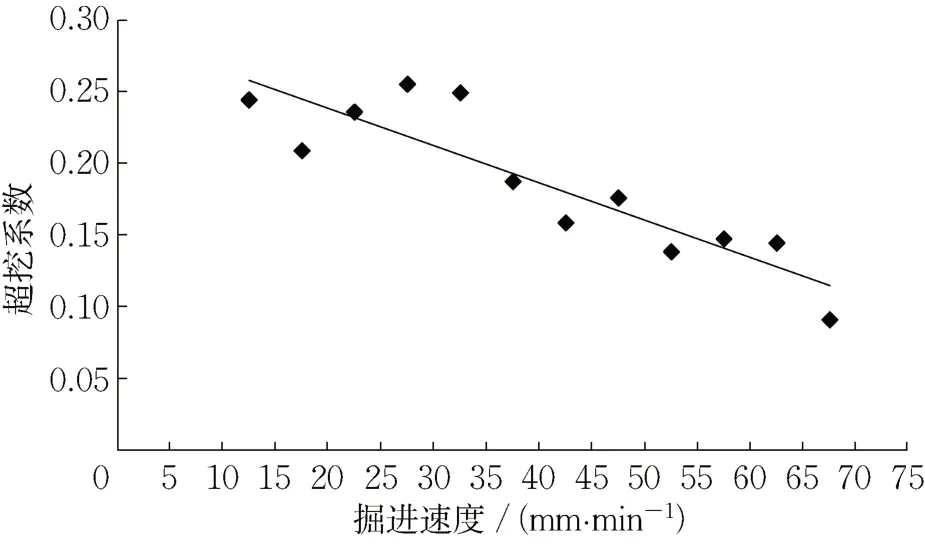
图12 超挖系数与刀盘扭矩的关系Fig.12 Over-excavation coefficient versus cutter head torque
综上所述,土仓压力设定过低会导致开挖面失稳,继而发生超挖,设定过高则容易出现刀盘卡死现象,盾构脱困会造成超挖。
因此,在砂卵石地层中应保持适度欠压掘进,针对本文中的开挖面失稳案例,盾构1#土仓压力应控制在75 kPa。
3.2 刀盘转速控制
根据3.1节中的分析,土仓压力过高时会增大刀盘背面的摩擦扭矩从而容易发生刀盘卡死现象。虽然刀盘扭矩无法主动调控,但可以通过调整刀盘转速进行间接控制。刀盘额定功率、额定扭矩和刀盘转速满足式(3)所示关系,以本文案例中海瑞克盾构机为例分析刀盘转速与扭矩间的关系,如图13所示。
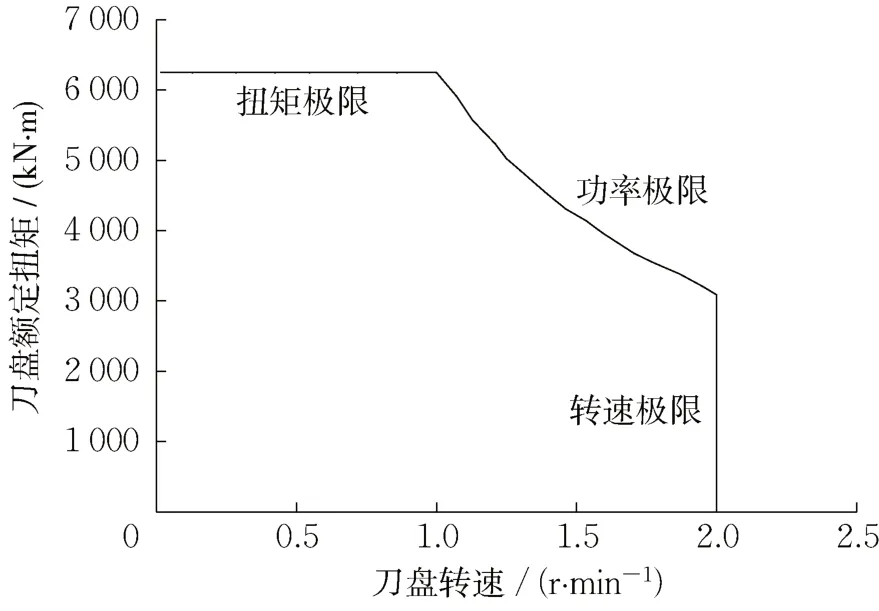
图13 刀盘额定功率、额定扭矩与刀盘转速的关系Fig. 13 Rated power and rated torque versus rotating speed of cutter head
式中:P为功率;T为额定扭矩;n为转速。
由刀盘驱动的调速特性可知,刀盘转速在0~1 r·min-1时,通过提高驱动功率可以使刀盘额定扭矩保持在6 228 kN·m,刀盘转速在1~2 r·min-1时,驱动系统到达额定功率后不再增加,刀盘额定扭矩随转速的增加而下降。为分析刀盘实际扭矩与刀盘转速间的关系,将实际施工中的刀盘转速每隔0.1 r·min-1划分一个区段,并将各刀盘转速区段中的刀盘实测扭矩取平均值,两者间关系如图14 所示,可知实测刀盘扭矩随刀盘转速的增加而增大。
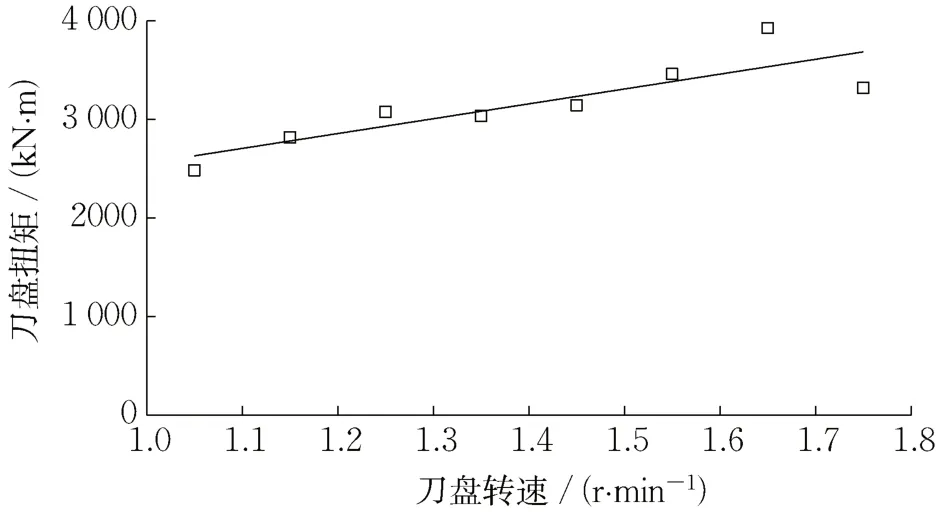
图14 刀盘转速与刀盘实际扭矩的关系Fig. 14 Rotating speed versus operation torque of cutter head
将上述刀盘转速与刀盘扭矩的关系绘入海瑞克盾构刀盘额定扭矩图中,如图15所示。

图15 盾构刀盘额定扭矩与实际扭矩对比Fig. 15 Comparison of rated torque and operation torque of cutter head
盾构正常掘进时刀盘转速在1~1.5 r·min-1范围内,刀盘额定扭矩相比于实际扭矩存在富余量,当刀盘转速大于1.5 r·min-1时,当盾构掘进遭遇高强度漂石或土仓压力设定过高,额定扭矩无法满足保持刀盘转动所需的扭矩要求,会造成刀盘卡死现象的发生,盾构刀盘脱困的过程中会导致超挖系数的升高。
因此,实际施工过程中应适当降低刀盘转速,为可能遇到的大粒径漂石和土仓压力控制预留足够的富余扭矩。同时,当盾构掘进遭遇不利于开挖的地层条件时,若长期保持高扭矩状态掘进也容易对开挖面前方造成较大扰动从而导致开挖面失稳。除了在盾构机能上获得更多的富余扭矩之外,掘进过程中也应向开挖面前方及土仓内注入渣土改良剂以增加渣土流塑性、降低摩擦力,同时降低盾构掘进的贯入度,通过多种手段联合控制尽快降低实际刀盘扭矩。
4 结论
基于成都砂卵石地层6 m级土压平衡盾构开挖面失稳超挖实例,针对开挖面失稳成因和发展过程开展了三维离散元分析,结合盾构超挖段实测数据,提出了开挖面稳定性控制方法。针对6 m级土压平衡盾构的砂卵石层施工,本文得到的主要结论为:
(1)开挖面失稳位置与支护力分布形式有关,采用梯形分布支护时,开挖面顶部最先失稳,采用均匀支护时,开挖面中心处最先失稳。梯形支护形式所需的极限支护力比均匀支护形式更大,对于本文计算案例,在2倍埋深条件下,梯形支护形式的开挖面极限支护力与静止土压力的比值为0.22。
(2)开挖面处于极限状态时,盾构上方0.75 D(D 为隧道直径)范围内产生土拱效应,范围内的竖向、侧向土压力均减小,侧土压力系数增大。开挖面发生失稳时,上方失稳区形状为椭球体。对于本文计算案例,当盾构埋深为2 D时,开挖面上方失稳区的最大高度为1.5 D,最大宽度为1.2 D,当支护力逐渐减小至0.1 P0(P0为静止土压力)时,失稳区发展到地面。
(3)砂卵石层超挖主要由两种因素造成,一种是土压力设置过低导致开挖面失稳产生超挖,一种是受刀盘额定扭矩制约,土仓压力过高后刀盘卡死,脱困过程中引起超挖。实际施工时应保持土仓适当欠压,并降低刀盘转速,为可能遇到的大粒径漂石和土仓压力控制预留足够的富余扭矩。
作者贡献声明:
姚琦钰:处理工程数据,开展盾构掘进参数分析,撰写论文。
张润来:实施数值模拟,绘制图表。
宫全美:提出研究课题,明确论文框架。
周顺华:指导研究工作,修改论文。

