基于渗率效应的可压缩智能同步注浆材料扩散机理研究
李利平, 曹阳阳, 丁传逵, 张益杰, 张 旭, 张延欢, 陈迪杨,宋增亮
(1. 山东大学 齐鲁交通学院,山东 济南 250100;2. 中铁十四局集团有限公司,山东 济南 250101;3. 山东大学 岩土工程中心,山东 济南250100)
城市轨道交通是解决人口膨胀、交通拥堵等问题和运输供需之间矛盾的有效途径[1-2]。目前,我国共53 座城市获得轨道交通规划批准,规划总里程约8 600 km[3]。盾构法是城市轨道交通隧道建设的主要手段[4-5],当盾构机掘进施工时,由于盾构机外壳直径大于管片直径,随着盾构机不断推进脱离管片,会在管片和围岩间形成环形空隙[6],此时周围岩土体处于脱空状态,在地应力作用下可能会诱发地层变形,需及时采用同步注浆填补空隙[7]。普通同步注浆材料可视为不可压缩浆液,在注浆压力作用下变形微小,往往忽略浆液受压缩时的变形[8-9]。浆液填充后由于渗透作用,盾尾间隙中的浆液质量不断减小,由于其不可压缩,导致盾尾间隙中浆液体积减小,若盾构掘进过程中,后续注浆不能及时补充,极易造成盾尾间隙空鼓,显著降低注浆质量[10-11],诱发地表沉降超限,甚至造成地面塌陷,因同步注浆造成的地面塌陷,时有发生。因此亟需研发能够具备“弹性”机制的智能浆液,在注浆压力作用下,浆液能够压缩,而随着浆液渗透固结,浆液压力减少时,能够及时补足渗透过程中浆液损失造成的孔隙[12-13]。而在浆液中添加适量气泡,可实现浆液受压过程收缩,卸压后膨胀的基本要求[14]。因此,本文将气泡加入浆材中,形成了可压缩智能同步注浆材料。智能轻质同步注浆材料具备体积、密度自适应调节能力,根据浆液向土体中扩散量,调整浆液的密度,从而保证浆液在盾尾区间内密实充填。
目前同步注浆理论均将浆材假定为不可压缩流体,而浆液中含有较多气泡时,浆液受压缩后,密度显著改变[15],其固结扩散机理如何变化,尚不清楚,因此在进行同步注浆时,需要对轻质智能材料同步注浆材料固结扩散机理进行研究[16]。明确注浆过程中浆液对管片的作用力和浆液在管片中密度变化情况,从而指导轻质智能同步注浆材料的施工[17-18]。
1 轻质智能同步注浆材料压缩理论模型
轻质智能同步注浆材料中,气泡含量达30 %以上,注浆过程中造成的浆液体积变化较大,不能忽略,因此需要研究浆液在压缩过程中密度与压力的关系。当浆液受压时,气泡含量气泡在浆液中受浮力、表面张力、粘性力、惯性力和液体压力作用。当浆液未受压缩时,气泡处于稳定状态,浮力、表面张力、粘性力、惯性力处于平衡状态,如图1 所示(p 为注浆压力)。
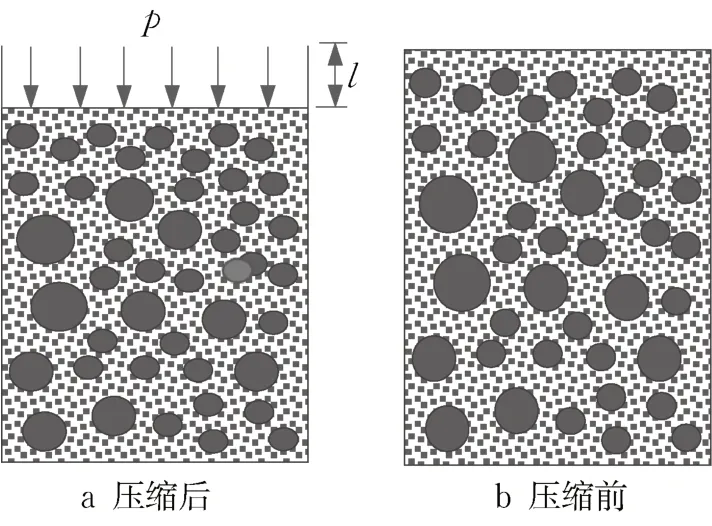
图1 气泡注浆材料压缩前后示意图Fig. 1 Schematic diagram of foam filling material before and after compression
当浆体受压之后,作用在浆体上的压力会传递至气泡,使气泡的体积缩小。当浆液粘度较小时,气泡体积收缩所造成的浮力、表面张力、粘性力和惯性力的变化远小于致其收缩的压力值。在气泡注浆材料中,假设只有气体是可压缩的,因此在研究气泡材料受压力后其密度变化规律时,可将浆液分解为气态浆体和固液混合浆体,如图2所示。

图2 气泡注浆材料受力等效图Fig. 2 Force equivalent diagram of foam filling material
假设气体浆体体积与气泡注浆材料总体体积之比为η,气泡在浆液中在不考虑热交换和浆液与气体之间相互作用时,由气体状态方程得:
式中:P1,P2分别为气态浆体与固液混合浆体的压强;V1,V2分别为气态浆体与固液混合浆体的体积。
浆液初始条件下,仅受初始大气压,因此式(1)可表示为
式中:Pch为常温常压(1 标准大气压)条件下的大气压强;Vch为初始气体体积;Vp为受到注浆压力p时的气体体积。
因此,受到注浆压力p时,浆液中的气体体积可表示为
因此,当注浆压力为p 时,浆液的密度ρ 可表示为
初始状态条件下,浆液中气体Vch与浆固混合体Vj可按式(5)和(6)表示:
式中:V为初始状态下浆体的总体积。
将式(3)、式(5)和式(6)代入式(4),得到浆液密度与注浆压力的关系表达式:
另外由于浆液内部粘聚力,气泡的表面张力,浆液表面摩擦力等原因,需要对该模型进行校正,校正系数分别为A,B,因此浆液密度与注浆压力关系表达式为
2 轻质智能同步注浆材料压力消散-固结机理
轻质智能同步注浆材料主要成分包括水、水泥等胶凝材料、骨料和气泡。在土层或砂层进行注浆时,水和粒径较小的胶凝材料能够渗透进入土层或砂层,而骨料和气泡粒径较大,不能通过孔隙进入土层或砂层的内部。在运用气泡基同步注浆材料进行注浆时,一定的注浆压力保证了浆液的体积富余,在注浆完成后,浆液中的水分和部分胶凝材料会渗入地层中,从而形成浆-土(砂)固结体。如图3 所示,在对浆液进行消散-固结分析时,应满足以下基本假定:

图3 同步注浆压力消散与固结示意图Fig. 3 Schematic diagram of simultaneous grouting pressure dissipation and consolidation
①假定地层中的孔隙水渗流符合达西定律;
②假定填充过程中,在单位时间内浆液压力不受后方已注入浆液的影响;
③假定土体变形为弹性变形;
④假定浆液扩散过程中,忽略气泡在浆-土交界面上对渗出浆液的阻滞作用。
在盾构隧道开挖过程对周围的土体产生一定程度的扰动,土体的孔隙率相较未扰动土体明显增大。根据叶飞对等效孔隙率的分析[1],扰动土层的厚度大致与盾尾间隙厚度相当。假定扰动后的土体变形仍服从广义胡克定律。
取范围内土体微元体作为研究对象。如图4所示,微元体包括盾尾间隙厚度(气泡浆厚度)x与浆液扩散区域厚度r。周围土体受浆液压力影响将发生位移,此位移在微元体中可近似表示为Δx。由于管片混凝土结构弹性模量远大于土体的弹性模量,因此可忽略微元体与管片外壁的接触效应。

图4 同步注浆压力消散与固结受力示意图Fig. 4 Schematic diagram of simultaneous grouting pressure dissipation and consolidation force
轻质智能同步注浆材料与周围土体相互作用方式,主要包括充填、压密和渗透。这三种状态并非独立存在。在充填和压密过程中,往往存在浆液的渗透。浆液充填和土体压密注浆过程较短,当充填注浆和压密注浆完成后,浆液仍在进行渗透,直至浆液固结。在浆液注入盾尾间隙后,浆液对土体压力与周围水土压力存在一定的压力差,但在较短时间内,应力的传递以及土体的协调变形,在浆液与土体接触面会建立起力学平衡,此时,浆液压力与土体的总应力相等,即:
式中:pg为浆液对土体的压力;σ1为地层的有效应力;pk为孔隙水压力。
当浆液压力大于孔隙水压力时,浆液就会向地层渗透,浆液渗透压力p可表示为
浆液的渗透压力p等于地层有效应力σ1,当渗透压力降为0时,渗透过程结束。浆液在凝固过程中,其减小的厚度为dx,隧道半径随之减小了dr,盾尾间隙中浆液质量的减小,导致了周围土体的卸荷,土体的有效应力降低了Δσr,浆液中的渗透压p 减小,如式(11)所示:
式中:σ0为初始地层有效应力。
基于广义胡克定律,得平面应变情况下其径向应变量Δεx为
式中:Δσr为微元体应力径向变化量;Δσθ为微元体切向方向的应力变化;E 为土体的弹性模量;μ 为土体的泊松比。
由于浆液的压力消散过程主要作用于土体的径向方向,因此Δσθ=0,进而可得:
式(13)—(15)中:dr为土体的径向变形量;G为土体的剪切模量。
结合式(10),可得:
式中:p0为初始的注浆渗透压力。
单位时间内单位面积的浆液的渗流量q,可表示为
式中:k为浆液的渗透系数;Δh为等效孔隙水压力的水头高差;y为时间t内形成的浆-土固结体厚度。根据质量守恒原理,因为浆体中气泡体积较大,渗入土体的主要为水和粒径较小的胶凝材料,因此,渗流量q可看作浆-土固结体孔隙体积变化量,可表示为
式中:ne,ni为浆-土固结体体积变化前后孔隙率;是单位时间内浆-土固结体形成的厚度。
结合式(14)和式(15),可得:
同时,隧道半径的减小量与浆-土固结体之比,等于浆-土固结前、后孔隙率的变化与土体体积之比,即:
等效压力水头高差Δh可以表示为
式中:Δp 为浆液渗透压的变化量,MPa;g 为重力密度,N·Kg-1;ρs为气泡浆液中可渗透部分的密度,在只有气泡、水和胶凝材料组成的材料中,ρs为水与胶凝材料混合体的密度。
联立式(16)—(18),可得浆液的固结方程为
其中,
对式(24)积分可得浆液向周边地层渗透过程中浆体的累计固结厚度。根据边界条件,t=0 时,x=0,微分方程的解为
式中:lambertW(C1)为朗伯W超越函数。
则注浆压力的方程为
当土层中不含孔隙水时,注浆压力可表示为
对于含有地下水情况,需要考虑地层渗透阻力对浆液压力消散影响。基于假定条件,根据达西定律可知:
式中:Q为单位时间断面总流量;A为断面面积;L为渗流长度
定义f为采用渗流时间表征的渗流阻力,根据式(29)可得:
因此,浆液中流体受到浆液自身的阻力为fg为
受到土层的渗流阻力为
以直径为R 的单位长度隧道为研究对象,单位时间内浆体流出量为Qg为
对于隧道周围地层渗透,半径r 的圆环处,单位时间的液体流量为Qk,可表示为
式中:h为盾尾间隙外侧R处与渗透半径r处的孔隙水压力高差;Ks为浆液在地层中的渗透系数。根据质量守恒原理,则有:
对式(35)进行积分,并根据边界条件r=R,h=0;r=H,h=h0
因此,当考虑地层渗流阻力对浆液渗透扩散影响时,浆液的固结方程为
随着浆液在压力过程中逐渐渗透,导致盾尾间隙内的浆液逐渐减少,在讨论浆液压力消散时,往往假设土体具有与浆液相同的收缩变形性,从而保证浆液能够始终与盾尾间隙外壁紧密接触,从而不影响浆液对盾尾间隙的填充和支撑。而实际工程中,采用普通浆液进行注浆时,往往土体的收缩变形不显著,导致盾尾间隙下部浆液渗透时,上部极易出现空鼓现象。而采用轻质智能同步注浆材料,当浆液中的水分向土体扩散时,浆液压力减小,即使土体不出现回弹变形,浆液压力变小所造成的体积增大,也能够填充整个盾尾间隙,从而避免了空鼓现象的发生,如图5所示。

图5 普通不可压缩浆液与轻质智能同步注浆材料压力消散过程Fig. 5 Pressure dissipation process of ordinary incompressible grouting and light grouting material
3 案例分析
国内某隧道管片外径15.76 m,盾尾间隙为0.15 m,覆土层厚度为20 m,上覆土层为粉质黏土、粉土、砂层,基岩为中生代燕山期晚期侵入岩辉长岩,其中盾构穿越地层为粉质黏土层,其天然含水率为29.8 %,土粒重度为1.77×106N·m-3,孔隙率为0.35,质量密度为1.81 g·cm-3。本案例注浆压力为0.32 MPa,压缩模量为4.2 MPa,剪切模量为9.8 MPa,泊松比为0.15,浆液初始渗透系数为4.2×10-8,注浆孔隙率0.35,固结体孔隙率为0.29,浆液的初始粘度为2.0 Pa·s,非气泡成分的水灰比为0.6,地层渗透阻力为0.9×103MPa·s·D-1·m-1。
3.1 轻质智能同步注浆材料压缩性参数确定
据式(8)可知,轻质智能注浆材料的受压时的密度与压力大小和浆液中气泡所占比例有关,为了阐明浆液在压缩过程中的密度演化机理,需进行浆液压缩特性试验,明确式(8)中的校正系数A和B。
本实验采用的容器为亚克力透明圆柱桶,高14 cm,内径为10 cm,上下采用橡胶环密封,活塞中设置通气孔,便于排气。试验机采用的岛津多功能试验机,加载速度为1 cm·min-1,如图6 所示。为了便于对比和计算,试验时对浆液进行定容,定容高度为12 cm。

图6 气泡基壁后注浆材料压缩特性试验磨具及压缩过程Fig. 6 Test tool and compression process for compression characteristics of foam base wall backfill material
图7为不同初始密度与不同砂胶比气泡基壁后注浆材料压缩曲线。
随着密度的增大,浆液中的气泡将随之减小,密度为1 000、1 200 和1 400 kg·m-3,气泡体积分别占浆液的74 %,43 %和28 %。由图可知,随着发泡剂占比的减小,浆液密度的增长速度明显更快,当压力为0.2 MPa 时,原始密度为1 000 kg·m-3的浆液已经达到了1 600 kg·m-3,超过1 200 kg·m-3和1 400 kg·m-3的浆液。当压力为0.7 MPa 时,初始密度为1 200 kg·m-3的浆液密度为1 760 kg·m-3,与初始密度为1 400 kg·m-3的浆液密度基本相等。图7b为不同砂胶比情况下气泡浆液在受压过程中密度变化曲线。砂胶比为1、2和2.5时,浆液中发泡剂体积分别为0.53、0.62和0.65,由图可知,随着砂胶比的不断增大,同等压力条件下的浆液,密度逐渐增大。受气体压缩特性影响,随着压力不断增大,密度首先出现较快的增长,达到0.3 MPa 后,密度变化趋于平缓。通过试验可知,浆液在压缩过程中,密度发生了较大变化,因此在进行注浆过程中,不能忽略密度变化对注浆过程的影响。
图8a为不同初始密度轻质智能同步注浆材料拟合曲线,随气泡占比η的降低,材料的初始密度逐渐上升,而参数B 随着η 降低而降低,说明B 与其具有显著的相关性。图8b 为不同砂浆比情况下的浆液的密度与压力拟合曲线,随着砂胶比变大,为了保证浆液的密度,其气泡含量将不断增大。初始密度为1 200 kg·m-3,砂胶比为2.5 的浆液拟合曲线,通过拟合得参数A 为0.615,B 为1.6。其关系式简化后如式(38)所示,通过该式建立了浆液压力与密度关系,为轻质智能同步注浆材料的扩散研究提供了基础。图9可得出气泡占比与参数B相关性。

图8 不同初始密度与不同砂胶比轻质智能注浆材料拟合曲线Fig. 8 Fitting curve of backfill material with different initial densities and sand-to-cement ratios
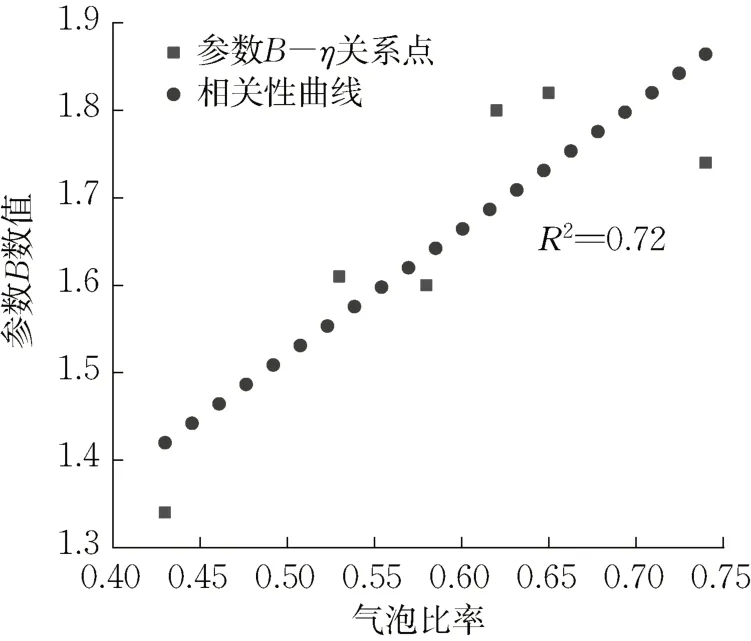
图9 气泡占比与参数B相关性Fig. 9 Correlation between proportion of foam and parameter B
3.2 轻质智能同步注浆材料固结过程分析
图10为在其他条件相同时,泊松比μ不同的条件下,浆液的固结状况和压力消散过程。由图可知,浆体的固结厚度随时间增大而增大,初期增长较快,后期增长趋缓。固结厚度在2.5~3.0 cm之间。在20 000 s之内,随着泊松比增大,浆体的固结速度逐渐增大,而超过20 000 s后,浆体的固结速度随着泊松比增大而减小。浆体压力则随着时间的推移,不断减小。由于本模型未考虑浆液的时变性,因此,在50 000 s之内,浆液压力降低较少,仅从0.32 MPa降低为0.316 MPa左右。

图10 不同泊松比条件下地层浆液固结与压力消散过程Fig. 10 Formation slurry consolidation and pressure dissipation process at different Poisson’s ratios
图11为不同注浆压力条件下地层浆液固结,由图可知,随着时间的不断推移,浆土固结厚度不断增大,当小于20 000 s 时,固结体厚度增长较快,而之后,增长速度明显降低。随着注浆压力的不断增大,增大浆体渗流动力,最终导致固结体厚度不断增大。

图11 不同注浆压力条件下地层浆液固结Fig. 11 Formation slurry consolidation at different grouting pressures
图12为本案例上述条件相同的情况下,不同渗透压力小件下,浆体的固结和压力消散过程曲线,由图可知,本次所取黏土的渗透量级为10-6,该渗透量级对应粉质黏土。由图可知,当渗透力较大时,较短时间内(500 s),浆液即可扩散至3 cm。随着渗透系数的降低,浆体渗透固结速率逐渐降低。对于浆液压力消散过程,浆液压力在500 s 之内,由于浆液的快速渗透而迅速减小,随后出现缓慢降低。对比上述低渗土层,说明土体的渗透系数对浆体的固结与压力消散有显著影响。
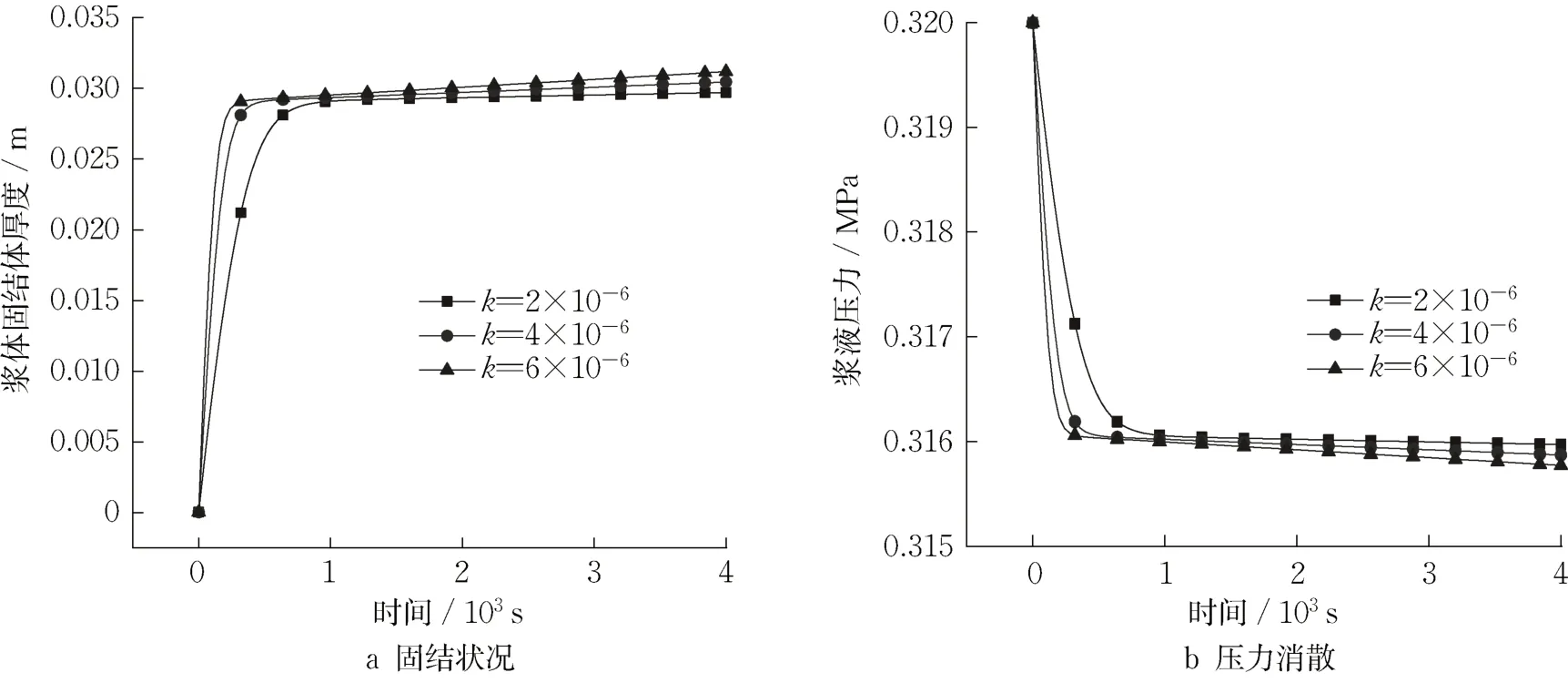
图12 不同渗透压力条件下地层浆液固结与压力消散过程Fig. 12 Formation slurry consolidation and pressure dissipation process under different osmotic pressure conditions
图13 为考虑不同渗流阻力的低渗土层浆体固结浆液固结与压力消散过程,由图可知,在低渗土层情况下,不同渗流阻力条件下的浆体固结过程和压力消散曲线基本重合,渗流阻力对浆液的固结和压力消散过程影响较小,而对比图14 可知,在高渗土层情况下,渗流阻力则有较大影响。在快速渗透阶段,不同渗透阻力固结曲线基本重合。最终固结厚度随渗流阻力增大而减小。

图13 考虑不同渗流阻力的低渗土层浆体固结浆液固结与压力消散过程Fig. 13 Slurry consolidation of low permeability soil layers considering different seepage resistances slurry consolidation and pressure dissipation process

图14 考虑不同渗流阻力的高渗土层浆体固结浆液固结与压力消散过程Fig. 14 Slurry consolidation of high permeability soil layers considering different seepage resistances slurry consolidation and pressure dissipation process
4 结论与展望
(1)轻质智能同步注浆材料压缩变形过程受初始密度影响显著,随着压力增大,浆液密度增大趋势逐渐变缓。浆液的初始密度和砂浆比对浆液受压后密度具有显著影响,初始密度增大,浆液更易受压,砂浆比增大,浆液压缩性能越好。
(2)轻质智能同步注浆材料固结过程受地层孔隙率影响较大,当孔隙率较小时,土体的其他特征参数对浆液固结过程中影响越小。
(3)当土体孔隙较大时,浆体的固结体厚度随泊松比增大而减小,随压力的增大而增大,渗流阻力越小,浆液的固结范围越大
作者贡献声明:
李利平:提供理论指导与主要思路。
曹阳阳:数值模拟与论文写作。
丁传逵:提供现场实际案例资料。
张益杰:数值模拟与论文写作。
张旭:提供现场实际案例资料。
张延欢:进行室内实验。
陈迪杨:进行室内实验。
宋增亮:进行室内实验。

