BOPPPS和对分课堂混合式教学模式实践研究

盛业青，旷菊红，关开中

（五邑大学，广东江门 529020）

OBE（Outcome Based Education）即成果导向教育，是一种围绕学生取得的成果去组织、实施和评价教学的教育模式。这里所说的成果，不仅仅是学生获得的书本知识，更重要的是对学生能力和素质的培养，包括对知识整体结构的把握和理解、多角度解决开放性问题等能力。OBE教育理念与当前我国高等教育领域所提倡的应用型人才培养模式契合[1]，关于OBE理念指导下的课堂改革，国内不同学科的学者进行了深入探究[2-5]。

1 常微分方程教学现状

常微分方程是理论数学与应用数学紧密结合的基础学科，是天文学、物理学、化学、生物学和某些社会科学中大量问题的精确数学描述的模型。通过分析微分方程的解，可以判断事件变化趋势，进而做出准确的决策。常微分方程具有高度抽象性、推理严谨性、应用广泛性等特点，能够培养学生的研究能力与逻辑思维能力。但在传统教学课堂上，师生之间缺乏高效互动，导致学生主动发现问题、解决问题、建构知识体系的能力无法提高，影响了学生研究能力和创新能力的培养。同时，传统讲授式课堂氛围不活跃，学生学习的主动性、积极性不高，很难达到预期的教学目标和效果。而近年来提倡的合作学习、参与式学习，存在学生准备时间过短、对新知识的吸收不足等问题，导致教学效果不佳。基于以上原因，课堂教学改革势在必行[6-9]。

2 BOPPPS教学模型与对分课堂简介

2.1 BOPPPS教学模型

BOPPPS模型是加拿大教师技能培训中心于1976年创建并被广泛采用的教学模式[10]，该模式强调以学生为中心的教学理念，重视教学互动和反馈。根据人的注意力大约只能持续维持15min的自然规律，将课堂教学内容划分为包括导入（Bridgein）、教学目标（Objective）、前测（Pre-assessment）、参与式学习（Participatory Learning）、后测（Postassessment）和总结（Summary）六个教学小单元（如图1所示），为有效开展课堂教学提供了可操作的具体实践流程，使得课堂教学的安排更加条理化、合理化，是协助教师明确教学目标、分析教学过程、发现教学问题、提升教学成效的有效工具。近年来，这一模式被引入高校教师培训和教学实践环节，在教学质量监控、慕课建设、专业课程教学研究等教学环节进行广泛探索和应用[11]。

图1 BOPPPS教学模型

2.2 对分课堂

对分课堂（PAD）是由复旦大学心理学系教授张学新提出的学生参与式教学方法，指把课堂时间一分为二，一部分留给教师讲授，另一部分留给学生讨论[12]。对分课堂将教学分为教师讲授（Presentation）、学生内化吸收（Assimilation）以及生生讨论、师生讨论（Discussion）三个环节，又称PAD课堂。在讲授环节，教师着重讲授课程内容的基本框架、重点、难点；课后，学生根据自己节奏完成教学内容的内化吸收，并在此过程中记录未理解的问题，再回到课堂分组讨论。强调先教后学，教师讲授在先，学生学习在后，强调生生、师生互动，鼓励自主性学习和参与式学习。这种教学模式可以充分适应不同学生的知识内化速度、内化方式及内化深度，目的是使学生变被动学习为主动学习，体现出以学生为中心的个性化学习过程。而课堂讨论环节则可以实现分享收获、答疑、解惑（生生答疑、师生答疑）的功能。与此同时，由于学生在内化吸收环节已进行了充分准备，回到课堂后，可以畅所欲言，发表自己的观点或就某个问题进行深入讨论，真正实现了生生互动、师生互动，这种参与式学习的课堂模式也在各学校进行了广泛的运用，并取得了较好的教学效果[11-15]。

3 BOPPPS教学模式与对分课堂混合式教学模式的实践应用——以“一阶线性微分方程及其运用”为例

3.1 学情分析

一阶线性微分方程是微分方程的一种特殊形式，是水污染防控分析、考古年代鉴定、镭衰变规律探究、RLC电路分析等自然界诸多实际问题的数学模型，也是高阶线性微分方程、一阶线性微分方程组内容开展学习的基础。学生掌握了所需要的一元函数微积分和可分离变量微分方程的求解方法，为此节课程的顺利开展奠定了基础。

3.2 教学设计思想

在实际教学中，教师根据教学内容和需要，在遵循BOPPPS的基本框架的基础上，抓住BOPPPS核心、突出BOPPPS特性，对教学模型进行重组或合并，俗称类BOPPPS教学模型（如图2所示）。

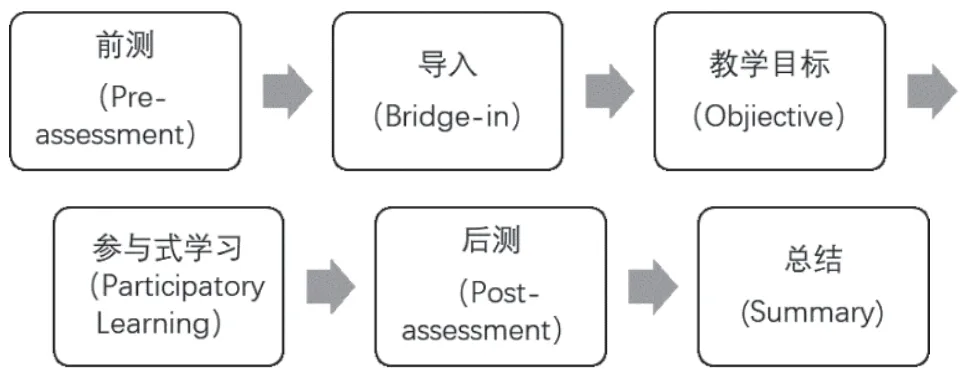
图2 类BOPPPS教学模型

如图3所示，BOPPPS结构中的参与式学习环节采用隔堂对分的模式，教师讲授重难点以及解题思路；学生在课上、课下独立内化吸收知识，完成“亮考帮”作业（总结收获、提出疑惑）；隔堂分组讨论“亮考帮”内容，进行生生互动、师生互动，促使学生主动学习、深入思考、加深印象。

图3 对分课堂教学模式

3.3 教学过程

（1）前测（P）：针对本节课的内容设计前测，要求学生课前线上完成回忆一阶齐次线性微分方程的通解以及与本节课程内容相关的不定积分求解两项任务。通过课前线上小测，检查学生对相关知识点的掌握情况，便于学生课前查缺补漏，从而上课时能够比较好地进行知识衔接，为本节课程的顺利开展奠定基础。

（2）问题导入（B）：播放阿根廷科尔福泻湖湖水受排放物污染变红的视频，对污染程度进行预测，从而为污染治理措施的制定提供依据，引发学生积极思考，从数学角度建立并求解微分方程模型。通过网络多媒体视频的播放，激发学生解决问题的兴趣。

（3）教学目标（O）：教学目标分为知识目标和能力目标，其中知识目标为：会判别给出的方程是否是一阶线性微分方程；会利用常数变易法和公式法求解一阶线性微分方程。能力目标为通过案例分析，培养学生发现问题、提出问题、思考问题、解决问题的能力。通过学生个人知识内化与反思总结，培养学生建构知识体系的能力。学生通过在知识讲授之前明确本节课的学习任务，带着任务去学习，做到有的放矢，提升课堂教学效果。

（4）参与式学习（P）：在探索知识点的过程中，通过概念引入、求解探究、知识内化、案例分析等环节，引导学生积极参与一阶线性微分方程求解过程。

在案例分析求解阶段，引导学生利用所学常数变易法或公式法，动手演算水污染数学模型根据所求结果分析案例中污染物变化的趋势，给出防治污染的必要性理论支撑。通过实际问题的求解，带领学生体会微分方程的应用。在教学过程中，培养学生理性思辨能力。同时，鼓励学生利用相关数学软件（比如MATLAB）验证所求结果的正确性，拓展学生的解题思路。

知识内化阶段是教师讲授完一阶线性微分方程的定义、求解方法以及案例解答后，给出5min时间，请学生在教师讲解的基础上，结合学习目标，以自己的节奏完成知识的内化吸收，通过绘制知识地图，独立完成知识体系的重新建构。同时，布置隔堂对分的“亮考帮”拓展作业，要求在下次课以小组的形式进行讨论，分别为展示自己掌握的内容即“亮”，考查同伴知识点掌握情况即“考”，以及就自己有疑惑的地方请求小组同伴或者教师的答疑解惑即“帮”。“亮考帮”作业的完成促进学生进行主动总结与反思，完成学习过程的自我反馈评价，实现自主性参与学习。

（5）后测（P）：后测分为三种形式，分别为课堂常规解题训练、课堂变式训练以及课后线上小测检查教学目标的达成情况。通过课堂常规习题，提升学生对常数变易法操作步骤的掌握程度，课堂变式训练是在知识内化的基础上进行知识点的变式和提升，引导学生探究一阶线性微分方程形式的本质，学会知识迁移。

（6）总结（S）：引导学生通过绘制本节课程的思维导图完成知识点的总结，学生通过自我总结完成知识的进一步建构。

4 效果反馈

笔者将BOPPPS和对分课堂混合式教学模式落实到一阶线性微分方程的教学实践中，得到参与学生的如下反馈（见图4～图7）。从反馈结果来看，BOPPPS模式的导入环节和学生的学习目标设定得到了90%以上学生的认可；而作为参与式学习实现方式的对分课堂方法，有80%的学生觉得通过对分课堂的“亮考帮”环节，加深了对知识点的理解，并且有超过60%的学生觉得“激发了主动学习的兴趣”“开拓了思维”，同时“锻炼了自身的沟通能力和表达能力”。但由于这种教学模式需要学生课后花费较多时间进行自主学习与知识建构，所以，有将近2/3的学生认为在适当的机会采用此课堂教学方法即可。

图4 导入环节学生反馈

图5 教学目标环节学生反馈

图6 对分课堂环节学生反馈

图7 实施混合式教学方法学生反馈

5 结语

运用BOPPPS和对分课堂混合式教学模式，既提供了可操作的具体课堂实践流程，同时参与式学习环节采用的对分课堂模式提高了学生的学习主动性和建构知识的能力，做到了OBE理念的以问题为导向、以学生为中心的有效课堂教学。同时需要说明的是，BOPPPS模式下的对分课堂教学法不必完全限制于固定结构，可在掌握本质、抓住精髓的前提下，根据情况做相应调整，进而实现有效教学。