基于旋转多普勒效应的自旋目标转速估计方法*

印必还 何姿 丁大志

(南京理工大学电子工程与光电技术学院,南京 210094)

旋转多普勒效应是携带轨道角动量的涡旋电磁波用于旋转目标探测时的一种重要现象.相比于传统平面波,旋转多普勒效应使得涡旋电磁波可以沿目标旋转轴方向探测到目标的自旋运动.然而,对于特定结构的自旋目标,利用整数阶轨道角动量波束进行探测仍然存在盲区.为了拓展基于旋转多普勒效应的探测方案的适用范围,本文基于时频分析方法,研究了在分数阶轨道角动量波束正入射和斜入射时自旋目标的转速估计方法.首先基于理想散射点模型,推导了其在整数阶和分数阶轨道角动量波束正入射和斜入射时的回波模型,以及理论时频曲线.其次,以三维实际目标为例,基于矩量法和短时傅里叶变换方法,得到目标在分数阶轨道角动量波束入射时的回波及其时频图,并从时频图中提取时频脊及其波动周期,以此估计目标自旋速度.结果证明,分数阶轨道角动量波束无论在正入射还是斜入射情况下均可有效地估计自旋目标的旋转速度,并且能够克服整数阶轨道角动量波束的探测盲区,在探测目标自旋运动时具有更广泛的适用性.

1 引言

自20 世纪90 年代在拉盖尔-高斯模式激光中发现轨道角动量(orbital angular momentum,OAM)以来[1],由于其理论上具备的高自由度特征,关于轨道角动量的研究迅速兴起.其中,由携带轨道角动量的涡旋电磁波引起的旋转多普勒效应是用于旋转目标探测的一种重要手段,在光学领域被发现迄今已超过20 年[2,3].旋转多普勒效应产生的根本原因是携带轨道角动量的涡旋波束具有螺旋状的等相位面[4,5],其坡印廷矢量有垂直于传播轴方向的分量,可以感知目标在传播截面内的横向运动,而此方向恰恰是传统平面波的探测盲区.目前轨道角动量的研究已逐步从光频段扩展到了射频微波频段[6−8],射频波段的旋转多普勒效应也引起了人们的关注和重视.2016 年,Zhao 等[9]提出了一种基于相位测量的间接转速估计方法,以此避免在微波波段提取微小的频移.Zheng 等[10]基于平面轨道角动量波束提出了一种矢量速度探测方案.Gong等[11]根据OAM 谱和频谱,实现了对自旋并平动目标的速度探测.Zhou 等[12]推导了在雷达单脉冲和多脉冲条件下的旋转多普勒分辨率.2022 年,本课题组[13]针对离散旋转对称体提出了一种基于分数阶轨道角动量波束的自旋探测方案,解决了在涡旋波正入射离散旋转对称体时部分整数模式失效的问题.然而,实际探测目标时,往往无法保证波束能正入射目标这种理想情况.在非理想入射情况下,回波模式的不纯导致了传统FFT 方法常常会因为边峰淹没主峰而无法提取理论峰值[10].针对这一问题,Luo 等[14],Li 等[15]和Wang 等[16]分别研究了整数模式涡旋波束在非理想入射情况下理想散射点和金属锥体的微动参数提取方法,而非理想入射情况下基于分数阶轨道角动量的相关研究目前还没有公开文献报道.本文接续此前的工作,针对非理想入射情况,研究了基于分数阶轨道角动量的自旋目标转速估计方法.文中以理想散射点模型为例,先后推导了分数阶轨道角动量波束正入射和斜入射自旋目标时的回波模型,并得到相应快速傅里叶变换(fast Fourier transform,FFT)频谱和理论时频曲线.随后以三维实际目标为例,用全波电磁计算方法获得相同场景下的回波,通过时频分析方法提取回波多普勒频率的波动周期,以此实现对自旋目标的转速估计.本文工作完善了基于分数阶轨道角动量的自旋目标探测方案,提升了其在实际目标探测中的可行性和适用性.

2 基于整数阶轨道角动量的旋转多普勒效应

2.1 理想入射情况

所谓理想入射情况,是指涡旋波束的波束轴与目标旋转轴重合并指向目标旋转中心,此时目标旋转平面与波束轴完全垂直,如图1 所示.

根据旋转多普勒理论,当被探测物体在与涡旋波束传播轴垂直的平面内绕轴旋转运动时,其轴向散射回波将在频域产生多普勒频移[17]:

其中l为拓扑电荷数或模式数;Ω为目标的旋转角速度.通常(1)式中的关系是成立的,但是在特定情况下它是不可用的.比如离散型旋转对称体(DBoR)在理想入射条件下就存在部分整数模式不可用的情况,这种结构通常有均匀对称分布的散射中心,如图2 所示.

图2 DBoR 散射中心分布情况Fig.2.The distribution of scattering centers for the DBoR.

不失一般性,假设入射波表示为[18]

其中k为波数;Al为模式l的幅度加权;ϕ为方位角.假设图2 中的N个散射点如图1 所示以角速度Ω绕轴旋转,散射系数为σ,收发机位于轴上并与目标相距R0,沿旋转轴入射,则回波可写为

根据(4)式和(5)式可以发现,只有特定的模式l=nN才是有效的,此时通过傅里叶变换得到的旋转多普勒频移和(1)式是一致的,而在其他模式下,回波相互干涉抵消.这一推导结果说明了整数模式用于探测特定结构时是存在盲区的,无论采用何种回波分析方法.

2.2 非理想入射情况

非理想入射情况有若干种,如目标旋转平面偏转[10,14],发射/接收器分置[10],目标旋转轴平移[14],波束轴偏离目标旋转中心[15,16]等.本文以目标旋转平面偏转的斜入射场景为例进行推导和仿真,而由于这些非理想情况最终都是导致辐射场模式谱和回波频谱的畸变,因此基于FFT 频谱法得到的结果和结论是类似的,并且由于这些非理想探测场景中目标的旋转在时间域上始终具有周期性特征,本文采用的回波建模方法和时频分析工具可以通用.

建立如图3 所示的坐标系,假设目标坐标系xyz和源坐标系XYZ平行且旋转轴z和波束轴Z重合,两坐标系相距Dz,目标坐标系绕x轴逆时针旋转角度ϕd得到旋转坐标系x'y'z',假设目标为一理想散射点,初始位置在x轴正半轴距离原点R处,绕z'轴以角速度Ω逆时针旋转,辐射源位于源坐标系原点处.经过时间t后,目标在自身坐标系下的坐标 (rx,ry,rz) 为

图3 目标旋转平面的偏转Fig.3.The deflection of the rotating plane.

此时目标到辐射源的距离r为

目标在源坐标系下的方位角ϕ为

沿用(2)式中的入射波表达式,此时的回波可写成:

对(9)式中和相位相关的指数项进行二阶泰勒展开可以得到[10]:

其中Rem(ϕd)是泰勒展开式的高阶余项.从(10)式可以发现,旋转平面的偏转导致了回波中出现了如 sinΩt,sin 2Ωt,sin2Ωt乃至更高次的相位调制项,这些调制项将导致回波频谱中主峰左右出现更多的边峰,从而对主峰位置的判断形成干扰.而此时回波的多普勒频率可表示为

从(11)式可以看出,该多普勒频率在时间域上是具有周期性的.

为了验证以上推论,取频率433 MHz,辐射源距离旋转平面10 m,理想散射点旋转半径0.1 m,转速300 r/s,采样率10.8 kHz,采样点512 个.下面给出了在模式1 下旋转平面偏转50°时的回波FFT 频谱和理论时频曲线.

从图4 可以看到,此时FFT 频谱出现了很高的边峰导致难以识别主峰位置,而时频曲线呈现余弦状周期波动,其周期为 2π/Ω即目标的旋转周期,以此可以估计目标转速.

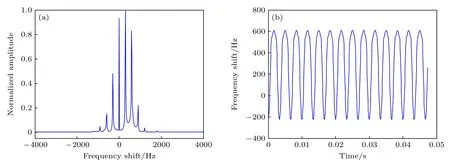
图4 回波频谱 (a) FFT 频谱;(b) 理论时频曲线Fig.4.The frequency spectrum of echo: (a) FFT spectrum;(b) theoretical time-frequency curve.

3 基于分数阶轨道角动量的旋转多普勒效应

3.1 理想入射情况

分数模式的轨道角动量可以分解为整数模式的傅里叶级数求和形式[19]:

其中的整数模式也被称为本征态,从(12)式可知,分数阶轨道角动量模态包含一系列整数模式,并且越接近分数l的整数模式m有越高的权重.这意味着分数阶轨道角动量波束用于目标探测相当于以不同权重的整数模式同时探测目标,既增加了回波包含的信息量,又避免了单一整数模式失效的问题.

同样以DBoR 模型为例,假设(2)式中的l是一个分数,将(12)式代入(2)式中可得

从(14)式和(15)式中可以看出,当l和N确定时,回波的频谱将会在f=f0+,m=nN,n∈Z 处出现峰值,并且当整数模式m越接近l时其权重越高.此推导显示了分数模式确保了回波频谱中有效模式的存在,避免了直接使用整数模式可能失效的情况.

为了证明以上推导,下面以理想辐射源进行解析计算,探测场景和图1 保持一致.令Al和σ等于1,f0=10 GHz,z0=3 m,r0=0.12 m,Ω=300 r/s.以半整数阶为例,在N和l不同取值下的回波频谱如图5—图7 所示.

图5 当 N=1 时的回波频谱 (a) l=0.5;(b) l=1.5(c) l=2.5;(d)l=3.5Fig.5.Echo frequency spectrums with N=1: (a) l=0.5;(b) l=1.5;(c) l=2.5;(d) l=3.5 .

图5 中,每个整数模式都是有效模式,并且每个半整数模式的回波频谱都有一对最高的谱线,对应于最接近l的整数模式,相邻谱线的频差为Ω/(2π),所以Ω=300×2π rad/s.图6 中,只有整数模式m=2n(n∈Z) 是有效模式而其他模式被抵消,剩下最高的谱线则对应于最接近l的有效模式,此时l1=0.5 和l2=1.5 对应的频谱是相互对称的,图6(b)和图6(c)中最高两根谱线的频差Δfd为 2Ω/(2π),所以Ω=600×2π/2=300×2π rad/s.图7 中,只有整数模式m=3n(n∈Z) 是有效模式而其他模式被抵消,此时l=1.5 对应的频谱有一对最高的谱线,在图7(b)中最高两根谱线的频差Δfd为 3Ω/2π,所以Ω=900×2π/3=300×2π rad/s.

图6 当 N=2 时的回波频谱 (a) l=0.5;(b) l=1.5;(c) l=2.5;(d)l=3.5Fig.6.Echo frequency spectrums with N=2: (a) l=0.5;(b) l=1.5;(c) l=2.5;(d) l=3.5 .

图7 当 N=3 时的回波频谱 (a) l=0.5;(b) l=1.5;(c) l=2.5;(d)l=3.5Fig.7.Echo frequency spectrums with N=3 and: (a) l=0.5;(b) l=1.5;(c) l=2.5;(d) l=3.5 .

综合以上讨论,可以总结出如下规律和结论.

1) 当N为1 时,对于任意半整数模式其回波频谱都有一对最高的谱线,例如图5.如果这两根最高的谱线频率差为 Δfd,则可以推出

2) 当N为奇数时(N＞1),对于模式l=N/2,其回波频谱具有一对最高的谱线,例如图7(b).如果这两根最高的谱线频率差为 Δfd,则可以推出

3) 当N为偶数时(N＞1),则模式l1=(N-1)/2和l2=(N+1)/2 的回波频谱是对称的,例如图6(a)和图6(b).如果频谱中两根最高的谱线频率差为 Δfd,则可以推出

至此,可以总结出基于分数阶轨道角动量的DBoR类目标的探测方案: 随着模式以l=0.5+n(n∈Z)的方式遍历,只要上述情形被识别出,则结构信息N和转速Ω可以通过(16)式—(18)式推出.

以上结果说明,分数模式在理想入射情况下不仅可以实现整数模式原本的旋转探测功能,同时还可以解决其探测盲区问题.

3.2 非理想入射情况

由于探测自旋目标时常常无法确保正好沿旋转轴方向入射,而涡旋电磁波周期性的相位梯度存在于沿以传播轴为中心的方位向上,一旦偏离此方向,回波将引入其他模式分量从而打乱原模式谱和频谱的分布规律.参考(10)式和(12)式,当模式为分数时,回波可以写为

显然,旋转平面偏转引入的相位调制项将作用到分数模式中包含的每一个整数模式上,同样会干扰各谱峰位置的判断.

下面以图7 中的问题为例,当目标旋转平面绕X轴偏转5°后(图8 所示),其回波频谱见图9.

图8 目标旋转平面偏转时的非理想入射情况Fig.8.The unideal illumination with the deflection of the rotating plane.

图9 当 N=3 时,旋转平面偏转后的回波频谱 (a) l=0.5;(b) l=1.5;(c) l=2.5;(d)l=3.5Fig.9.Echo frequency spectrums after the tilt of rotation plane with N=3: (a) l=0.5;(b) l=1.5;(c) l=2.5;(d) l=3.5 .

从图9 中可以看到,旋转平面的偏转造成回波频谱被打乱,谱线已不再具备3.1 节中所提到的规律性分布,相应的转速估计方法也由此失效.虽然在频谱上不再具备可供识别的特征和规律,但由于目标在时间域上仍属于周期性运动,其多普勒频率理论上依然遵循如(11)式所体现的周期性,而传统的FFT 变换并不能体现回波的瞬时特性,因此可以考虑用于分析非稳态信号的时频分析类方法.图10 和图11 分别给出了利用短时傅里叶变换得到的模式1.5 和2.5 对应的时频图.

图10 旋转平面偏转后模式1.5 回波时频图及其局部放大Fig.10.Echo frequency time-frequency graphs of mode 1.5 after the tilt of rotation plane and its local zoom.

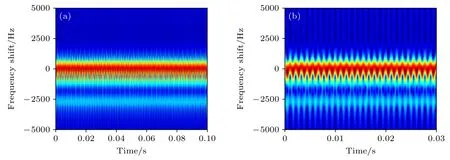
图11 旋转平面偏转后模式2.5 回波时频图及其局部放大Fig.11.Echo frequency time-frequency graphs of mode 2.5 after the tilt of rotation plane and its local zoom.

可见,时频图中的频率分量随时间呈周期性波动,并且其波动频率正比于目标自旋速度,可作为推测目标自旋速度的直接依据.

4 全波仿真与验证

本节基于全波电磁计算方法矩量法及其快速方法,验证了分数模式涡旋电磁波结合时频分析方法估计自旋目标转速的可行性.以风速仪模型(图12所示)为例,如2.1 节所述,这种典型的DBoR 结构在正入射时整数模式存在普遍的失效问题.

图12 风速仪模型Fig.12.The anemoscope model.

仿真场景和图8 类似,其中目标以20 r/s 的速度绕轴自旋,辐射源距离目标0.5 m,计算频率为10 GHz,采样率为720 Hz.分数模式OAM 波束的生成采用了文献[20]中的均匀圆阵方案,其中圆阵半径为9 cm,单元数为24,用于合成分数模式的整数模式范围为–10 到10,单元为理想电偶极子并沿Y方向放置在XOY平面内.电场的Y分量沿垂直距离0.5 m,俯仰角 8°的圆环上采样得到的辐射场模式谱和方位角相位梯度如图13 所示.

图13 辐射电场的相位梯度以及模式谱 (a) l=0.5;(b) l=1.5;(c) l=2.5;(d)l=3.5Fig.13.Phase gradients and mode spectrums of the radiation electric field with: (a) l=0.5(b) l=1.5(c) l=2.5(d) l=3.5 .

从图13 可以看到,这种方法产生的分数阶轨道角动量波束和理论一致包含了对称分布的整数模式,轻微的差异来自于场合成公式中的近似以及辐射单元的非均匀性,同时在方位角向产生了连续的相位梯度,除了在0°和360°附近由于相位不一致而导致的跳变.图14 和图15 分别给出了这些分数模式OAM波束在正入射和斜入射(目标绕Y轴偏转5°)该自旋目标时的回波FFT 频谱.

图14 当 N=3 时的回波频谱 (a) l=0.5;(b) l=1.5;(c) l=2.5;(d)l=3.5Fig.14.Echo frequency spectrums with N=3: (a) l=0.5;(b) l=1.5;(c) l=2.5;(d) l=3.5 .

图15 当 N=3 时,旋转平面偏转后的回波频谱 (a) l=0.5;(b) l=1.5;(c) l=2.5;(d)l=3.5Fig.15.Echo frequency spectrums after the tilt of rotation plane with N=3: (a) l=0.5;(b) l=1.5;(c) l=2.5;(d) l=3.5 .

从回波频谱可以看出,分数模式OAM 波束正入射该目标时的结果和理论基本一致.而旋转平面的偏转扰乱了谱线分布,例如模式1.5 对应频谱不再对称,模式2.5 和模式3.5 对应频谱峰值发生了偏移,显然此时已无法运用正入射时的相关推论进行转速估计.根据参考文献[11],本文所研究问题的回波频谱可以表示为

其中f0为载频,δ(·) 表示冲击响应函数,即回波频谱在去除载频后相当于模式谱以系数加权得到,所以模式谱的分布直接影响了回波频谱的分布.而无论整数模式或是分数模式,其连续的相位梯度都是存在于垂直于波束轴平面内的方位角向上,偏离此方向的辐射或接收都会导致模式谱的畸变,进而导致回波频谱的畸变,这也是为什么在非理想收发条件下无法直接从回波频谱获取有效信息的原因.

由于斜入射时的频域特征难以识别,考虑到目标在时间上是周期运动,通过时频分析方法获取目标运动周期是一种可行的途径.下面给出了回波经短时傅里叶变换后的时频图以及提取的时频脊.

根据图16(b)和图17(b)提取得到的时频曲线,分别测量其中8 个波动周期的长度均约为0.133 s,即每个周期约为0.0167 s,考虑到此模型每转120°即是一个周期,实际的旋转周期为0.0167×3≈0.05 s,即旋转频率约为20 Hz,即转速约为20 r/s,近似等于理论值.该全波仿真验证了利用分数模式OAM 结合时频分析方法进行自旋目标转速估计,相比于整数模式和FFT 频谱法具有更广泛的适用性和有效性.

图16 模式0.5 波束正入射目标时的时频图及时频曲线 (a) 时频图;(b) 时频曲线Fig.16.Time-frequency graph and curve under the normal incidence of the beam with mode 0.5: (a) Time-frequency map;(b) timefrequency curve.

图17 模式2.5 波束斜入射目标时(旋转平面绕Y 轴倾斜5°)的时频图及时频曲线 (a) 时频图;(b) 时频曲线Fig.17.Time-frequency graph and curve under the oblique incidence (the plane of rotation tilts around Y axis with 5°) of the beam with mode 2.5: (a) Time-frequency map;(b) time-frequency curve.

5 结论

本文讨论了基于整数阶和分数阶轨道角动量的旋转多普勒效应.相关结果证明,分数阶轨道角动量波束无论在正入射还是斜入射自旋目标时,回波时频图都具有周期性波动的时频脊,并能够以此有效估计目标自旋速度.而对于正入射离散旋转对称体时整数模式失效的情况,利用分数模式依然可以有效估计目标自旋速度.相比于此前的研究工作,本文将基于分数阶轨道角动量的旋转多普勒效应研究从正入射场景扩展到了斜入射场景,在传统FFT 方法已无法估计目标转速的情况下,以时频分析方法提取多普勒频率变化周期并以此估计目标自旋速度.该工作进一步完善了基于分数阶轨道角动量的旋转多普勒效应研究,相关结果可为基于旋转多普勒效应的雷达探测方案提供参考和借鉴.