磁性拓扑绝缘体中的量子输运现象*
刘畅 王亚愚
1) (中国人民大学物理系,光电功能与微纳器件北京市重点实验室,北京 100872)
2) (中国人民大学,量子态构筑与调控教育部重点实验室,北京 100872)
3) (清华大学物理系,低维量子物理国家重点实验室,北京 100084)
4) (量子信息前沿科学中心,北京 100084)
5) (合肥国家实验室,合肥 230088)
磁性拓扑绝缘体是过去十年里凝聚态物理学领域的一个重要研究方向,其拓扑非平庸能带结构与自旋、轨道、电荷、维度等自由度之间的相互作用可以产生丰富的拓扑量子物态和拓扑相变现象.对磁性拓扑绝缘体输运性质的研究是探索其新奇物性的重要手段,对于深入理解拓扑量子物态以及开发新型低功耗电子学器件具有重要意义.本文回顾了近年来磁性拓扑绝缘体输运实验方面的重要研究进展,包括磁性掺杂拓扑绝缘体中的量子反常霍尔效应和拓扑量子相变现象、本征反铁磁拓扑绝缘体MnBi2Te4 中的量子反常霍尔相、轴子绝缘体相和陈绝缘体相,以及在脉冲强磁场下陈绝缘体演化出的螺旋式拓扑物态.最后,本文对未来磁性拓扑绝缘体研究的方向和该体系中尚未充分理解的输运现象进行了分析和展望.
1 引言
在20 世纪80 年代,人们在低温强磁场条件下的二维电子气中观测到量子霍尔效应,开启了凝聚态物理学家关于拓扑量子物理研究的大门[1-3].由于量子霍尔效应起源于二维电子气在强磁场下形成的朗道能级,相变前后不涉及任何自发对称性破缺,因此无法用经典朗道相变理论来描述.1982 年,Thouless 等[4]基于贝里曲率在动量空间的积分,发现在量子霍尔效应中,电子波函数存在非平庸拓扑结构,建立了非零整数的拓扑不变量(称为TKNN 不变量)和量子化霍尔电导之间的普适内禀关系.这一重要发现首次将实验上可观测物理量和数学上拓扑的概念联系在一起.自此之后,寻找和实现具有量子化输运性质的新型拓扑量子物态成为凝聚态物理学的重要目标.在过去的三十年时间里,理论上提出了许多实现新型拓扑量子物态的方案.例如,1988 年美国物理学家Haldane[5,6]基于石墨烯晶格提出了一种模型,利用空间周期性磁场破坏时间反演对称性实现无朗道能级的量子霍尔效应,这一效应后来被称为量子反常霍尔效应或陈绝缘体.2003 年日本物理学家Onoda 和Nagaosa[7]考虑安德森局域化机制,提出在铁磁金属中引入无序实现量子化反常霍尔效应的理论方案.然而在很长一段时间里,由于缺乏合适的材料,实验方向一直进展缓慢,极端条件下形成的量子霍尔系统几乎是实验上实现拓扑量子物态的唯一途径.直到2005 年,拓扑绝缘体概念的提出才为后人在实验上实现多种具有量子化输运特性的新奇拓扑量子物态提供了可能[8-14].理论上,通过在三维拓扑绝缘体中引入磁性破坏时间反演对称性,可以使具有线性色散的拓扑表面态打开能隙,引起具有单个狄拉克锥的拓扑表面态出现半整数量子霍尔电导σxy=0.5e2/h,其中e是电子电荷,h是普朗克常数,这种半整数量子化现象与量子场论中的宇称反常(parity anomaly)密切相关[15-18].利用这种半整数量子化原理,磁性拓扑绝缘体可以实现量子反常霍尔效应[19-21]、轴子绝缘体相[22-25]和量子化拓扑磁电效应[26-28]等多种新奇拓扑物态和拓扑现象.这些新奇物态不仅具有重要的基础科学研究价值,而且在低功耗器件制备、标准计量和拓扑量子计算等领域具有巨大的应用潜力.因此在过去十年中,磁性拓扑绝缘体引起了全球物理学家的广泛关注,成为凝聚态物理研究的焦点和前沿.
在拓扑绝缘体中掺杂过渡族元素,是实现磁性拓扑绝缘体最广泛采用的手段之一[29-34].2013 年,由薛其坤领导的清华大学和中国科学院物理研究所联合团队[35],通过分子束外延方法成功生长了厚度为5 nm 的Cr 掺杂(Bi,Sb)2Te3磁性拓扑绝缘体薄膜,首次在实验上实现了量子反常霍尔效应,在极低温和零磁场下观测到量子化霍尔电阻率ρyx=h/e2和消失的纵向电阻率ρxx=0.两年后,日本东京大学[36]、美国加州大学洛杉矶分校[37]和麻省理工学院[38]等多个研究组也在相同体系中观测到该效应.之后几年,研究通过发展调制掺杂[39]和磁性共掺杂[40]两种方法,成功将量子反常霍尔效应的观测温度从30 mK 提升至1 K 以上.作为一种不依赖外磁场且基于全新原理的量子霍尔效应,量子反常霍尔效应为各种新奇量子态构筑和拓扑相变研究提供了新的平台.然而,随着成像和谱学研究的开展,人们发现磁性掺杂拓扑绝缘体中不可避免地存在各种无序,无序不仅破坏了系统的平移周期性,对电子输运产生显著影响,还严重制约了量子化温度的提升,极大地提高了基础研究和器件应用的门槛[41-48].因此,寻找具有本征磁序的拓扑绝缘体成为过去几年拓扑物态领域研究的一个热点问题[49,50].2019 年,一种新型的具有本征反铁磁性的拓扑绝缘体MnBi2Te4在实验上被首次发现,在凝聚态物理和材料科学领域引起广泛关注[51-55].作为实验上第一个兼备范德瓦耳斯层状特性、本征磁序以及拓扑能带的新型量子材料,MnBi2Te4完美地结合了拓扑材料和二维磁性材料的优势,研究者们可以通过分子束外延方法直接生长MnBi2Te4薄膜[51],或者通过二维材料中机械剥离的方法直接将单晶解理到薄层[56-58],同时保持其拓扑非平庸特性.此外,MnBi2Te4特殊的层内铁磁和层间反铁磁构型使得其磁结构可以通过不同方向的外磁场进行调控,极大地拓展了对磁性和拓扑之间相互作用的调控自由度[59-61].MnBi2Te4的发现为探索各种新奇拓扑量子现象开辟了新的方向.
近年来,利用输运手段,人们在磁性拓扑绝缘体中拓扑量子物态和拓扑相变研究方面取得了许多重要进展(如图1 所示)[35-40,51-58,62-82].本综述将着重介绍近年来磁性拓扑绝缘体输运研究方面的研究成果,并主要围绕作者在这两个方面的重要工作以及相关物理问题进行展开.本文第2 节将首先对磁性拓扑绝缘体的晶体结构、磁结构和电子结构等基本物性进行介绍.第3 节将介绍各种拓扑量子物态的输运性质以及他们之间的拓扑相变,其中第一部分围绕磁性掺杂拓扑绝缘体展开,主要介绍量子反常霍尔效应的优化、无序引起的不同量子反常霍尔基态以及反常霍尔效应手性问题;第二部分将重点介绍本征磁性拓扑绝缘体MnBi2Te4的输运实验进展,包括零磁场奇数层样品中的量子反常霍尔效应、零磁场偶数层样品中的轴子绝缘体相、高磁场少层样品中的陈绝缘体相以及脉冲强磁场少层样品中的螺旋式陈绝缘体相.最后,基于目前的一些最新的理论和实验工作,展望磁性拓扑绝缘体研究未来的发展方向.

图1 磁性拓扑绝缘体中关于拓扑量子物态和拓扑相变研究的关键进展时间线Fig.1.Timeline of the key developments in the studies of topological quantum state and topological phase transition in magnetic TIs.
2 磁性拓扑绝缘体的晶体、磁性和电子结构
2.1 磁性掺杂拓扑绝缘体
目前国际上研究最广泛的磁性拓扑绝缘体主要是基于Bi2Te3家族的V-VI 族化合物半导体[83-85],其成员包括Bi2Te3,Bi2Se3和Sb2Te3.在拓扑绝缘体概念被提出以前,Bi2Te3家族成员作为性能优良的传统热电材料,已经被大量应用于制冷器件中.Bi2Te3单晶可以看成由Te-Bi-Te-Bi-Te 五个原子密排组成的五原子层(quintuple layer,QL)沿c轴方向堆叠而成,其晶体结构属于斜方六面体晶系,其中每个QL 内部Bi 和Te 原子之间通过共价键方式连接,相邻两层QL 通过Te 原子之间的范德瓦耳斯作用连接.目前实验上研究最多的磁性掺杂拓扑绝缘体主要是通过在Bi2Te3家族成员中掺杂少量过渡族元素(例如如V,Cr 和Mn)取代Bi元素获得[31-33,35,38],因此其磁性在空间的分布存在一定的随机性[41-48],其层状结构如图2(a)所示.由于在材料生长过程中采用的方法和参数不同,Bi2Te3家族拓扑绝缘体在材料内部会形成各种缺陷和杂质,造成真实材料表现出严重的空穴型或者电子型掺杂.因此想要获得体态绝缘的磁性拓扑绝缘体,研究者往往需要通过能带工程,将具有不同载流子的拓扑绝缘体进行混合(例如电子型的Bi2Te3和空穴型的Sb2Te3)[86].这种合金化和磁性掺杂过程会引起磁性掺杂拓扑绝缘体中出现强烈的化学势涨落和磁无序,并对局域磁性和电子输运性质产生显著影响[41-48].尽管受到无序的影响,实验上发现磁性掺杂仍然可以在介观尺度上获得长程磁有序.通过对磁性掺杂拓扑绝缘体的输运性质和磁性进行研究,人们已经发现了Ruderman-Kittel-Kasuya-Yosida (RKKY)和Van Vleck 两种不同磁序起源的机制.2012 年,日本东京大学Tokura 研究组[31,87]在解理获得的Mn 掺杂Bi2Te3—ySey拓扑绝缘体薄片中开展了栅压调控的输运测量,发现该体系的磁性主要通过表面态狄拉克电子传导,铁磁性居里温度Tc强烈依赖于载流子浓度,其行为符合表面态电子传导的RKKY 机制,这种表面态传导的磁性机制在扫描隧道显微谱学实验中也得到了证实[88].2013 年,清华大学薛其坤研究组[19,33]生长了不同组分的Cr 掺杂(BixSb1—x)2Te3薄膜,并对其电子结构和霍尔效应进行测量,发现该体系铁磁序与载流子无关,这和理论预言的由量子力学二阶微扰引起的Van Vleck 机制相吻合,随后研究者在V 掺杂的Sb2Te3体系的低能电子能量损失谱实验中也证实了Van Vleck 机制[89],这种不依赖于载流子的铁磁序机制,保证了体态绝缘的量子反常霍尔效应样品中时间反演对称性的破缺.同年,美国加州大学洛杉矶分校Wang 研究组[34]通过改变磁性拓扑绝缘体(BixSb1—x)2Te3中的Cr 掺杂浓度,发现RKKY 和Van Vleck 两种磁性机制可以共存,这些发现激发了研究者们对磁性和拓扑相互作用的不断探索.过去十年,人们已经在磁性掺杂拓扑绝缘体中发现了许多新奇拓扑物理现象,包括量子反常霍尔效应[35-37]、轴子绝缘体[70-72]、拓扑霍尔效应[68,69,90]、拓扑磁电效应[91]和量子化法拉第效应[92,93]等,揭示了不同拓扑物态之间丰富的相变行为[36,64,67,77].在应用探索方面,人们开展了一系列基于拓扑绝缘体表面态的自旋电子学测量[94],发现了拓扑表面态引起的巨大的自旋轨道矩[95-97];通过对量子化电阻数值的精密测量,实现了利用量子反常霍尔效应进行标准电阻计量[80,98-100].
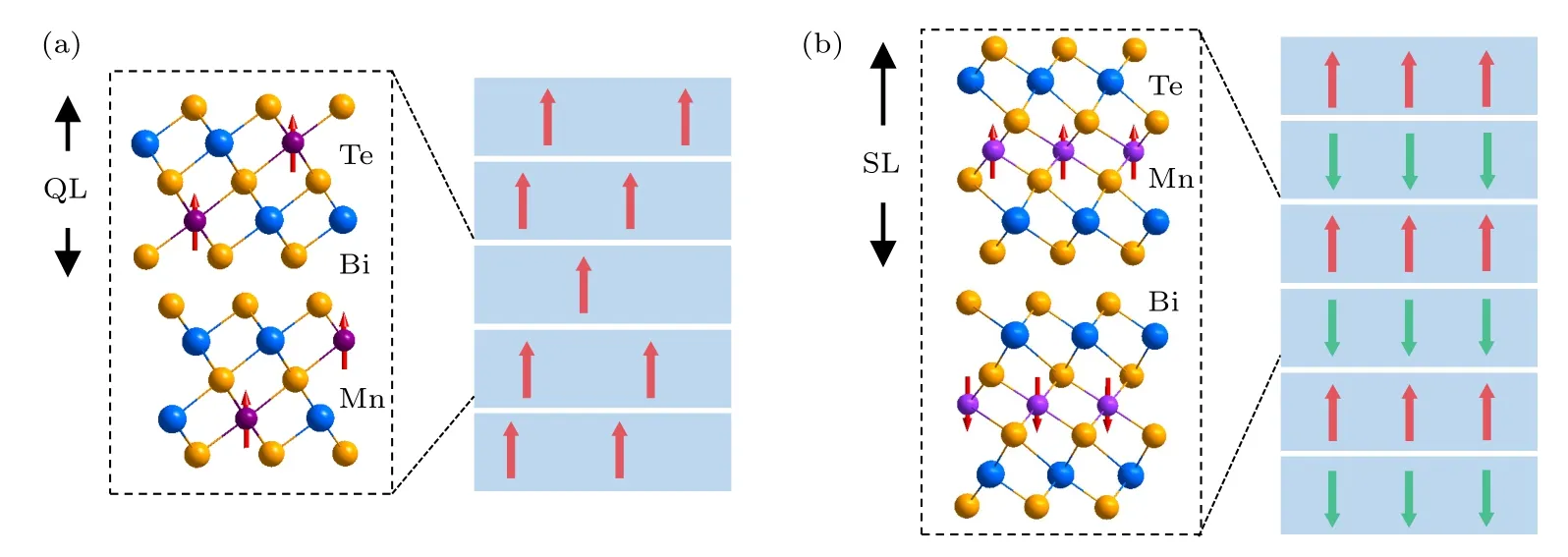
图2 磁性拓扑绝缘体结构示意图 (a)磁性掺杂拓扑绝缘体MnxBi2—xTe3 晶格结构和磁结构,红色箭头表示随机分布磁矩的磁化方向;(b)本征反铁磁拓扑绝缘体MnBi2Te4 的晶格结构和磁结构,红色和绿色箭头表示层间反平行排列磁矩的磁化方向Fig.2.Schematic layer structure of magnetic topological insulators (TIs): (a) Crystal and magnetic structures of magnetically doped TI MnxBi2—xTe3,the red arrows represent the magnetizations of the randomly distributed magnetic moments;(b) crystal and magnetic structures of the intrinsic AFM TI MnBi2Te4.The red and green arrows denote the magnetization of the oppositely aligned magnetic moments between neighboring layers.
2.2 本征磁性拓扑绝缘体
关于本征磁性拓扑绝缘体MnBi2Te4的研究最早可以追述到2013 年,韩国科学家[101]在研究V-VI 族半导体热电性质时,首先通过固态熔融方法在实验上合成了MnBi2Te4单晶,然而当时作者并没有涉及任何拓扑性的研究,因此该工作并未引起拓扑物理领域太多的关注.直到2019 年清华大学薛其坤和何珂团队[51]通过分子束外延的方法生长了MnBi2Te4薄膜,并利用角分辨光电子能谱观测到具有线性色散的狄拉克表面态,同时结合磁化测量,首次从实验上证明了该体系是一类新型的具有本征反铁磁序的拓扑绝缘体.在理论方面,2019年,南京大学张海军团队、复旦大学王靖团队、清华大学徐勇团队和西班牙CSIC-UPV/EHU 联合中心的Chulkov 团队[52,53,55]通过计算,分别预言了该体系中存在丰富的拓扑物态.通过调控磁性、维度和拓扑之间的相互作用,MnBi2Te4会在不同参数空间表现为量子反常霍尔效应、轴子绝缘体相、量子自旋霍尔绝缘体相、外尔半金属相和狄拉克半金属相等多种拓扑物态.至此之后,国际上掀起了关于MnBi2Te4中新奇拓扑物性研究的热潮[56-58,78,81,102-113].
MnBi2Te4作为一种二维材料,其块体单晶可以看成由Te-Bi-Te-Mn-Te-Bi-Te 构成的七原子层(septuple layer,SL)沿着c轴方向堆垛而成,其层状晶体结构和磁结构如图2(b)所示,和Bi2Te3中的QL 结构相比,MnBi2Te4中的七原子层可以看成厚度为1 个QL 的Bi2Te3在内部插上一层MnTe获得,因此与Bi2Te3拓扑绝缘体类似,MnBi2Te4每个SL 内部原子通过共价键方式连接,相邻SL 则通过范德瓦耳斯相互作用连接,实验上可以通过机械剥离的方式将MnBi2Te4从单晶解理到少层.在单晶生长方面,研究者们目前可以通过多种方法生长MnBi2Te4单晶,包括固态熔融法、助熔剂法和化学气相输运等方法[75,114-117].磁性方面,MnBi2Te4展现了与传统磁性掺杂拓扑绝缘体不同的特点.在传统磁性掺杂体系中,取决于过渡族元素种类、掺杂浓度以及拓扑绝缘体母体的选择,系统会表现为顺磁性或铁磁性[118].而在MnBi2Te4中,中子散射和磁力显微镜成像实验表明其单晶具有层状A 型反铁磁结构[119-121],每个SL 内部Mn 离子之间平行排列,而相邻SL 之间Mn 离子则反平行排列,因此可以通过施加不同方向的磁场调控其磁结构.不同温度下的磁化和电阻测量表明(如图3(a)所示),MnBi2Te4单晶反铁磁奈尔温度TN在25 K 左右[107],在沿着c轴方向的10 T 磁场中每个Mn 离子可以贡献3.9µB磁矩[122],在超过50 T 磁场时饱和磁化接近4.6µB,其中µB为玻尔磁矩.随着厚度的减小,MnBi2Te4中反铁磁序形成温度会逐渐下降,尽管如此,在单层极限下,实验上仍然可以在15 K 温度以下观测到长程铁磁序[113].值得关注的是,少层MnBi2Te4的磁性会表现出显著的层厚依赖的行为,例如北京大学叶堉研究组[113]和美国华盛顿大学许晓栋研究组[110]分别独立利用反射型磁圆二向色谱(RMCD),研究了不同层厚MnBi2Te4的光学信号在磁场下的响应,观测到其在低磁场反铁磁态展现出明显的奇偶振荡行为(如图3(b)所示).相比普通磁性掺杂拓扑绝缘体,MnBi2Te4最大的优势来自其严格化学配比的组分以及本征磁性,这些特点极大地克服了磁性掺杂引起的无序性,理论计算发现其在少层时表面态磁能隙可以高达38 meV,因此有望在高温实现各种拓扑量子物态[52].尽管早期有角分辨光电子能谱(ARPES)报道观测到超过60 meV 的磁能隙[53,123],然而,随着越来越多更加细致测量的开展,实验发现MnBi2Te4表面的磁能隙远小于理论预期值,大部分研究组在TN以下并未观测到明显的能隙打开过程[105-109].例如清华大学杨乐仙团队[107]通过高分辨laser-ARPES 测量了MnBi2Te4单晶在7 K 时的能带结构,发现其拓扑表面态仍然保持线性色散,在2.5 meV 的分辨率下没有任何能隙打开的迹象(如图3(c)所示).目前关于MnBi2Te4表面态能隙问题仍然存在着许多争议,特别是输运上观测到的量子反常霍尔效应[56]和轴子绝缘体超过100 MΩ 的体态电阻[57,124]都表明MnBi2Te4体态应该具有高度的绝缘性,这与ARPES 观测不到能隙并不吻合.目前理论上提出了包括反铁磁畴[107]、表面磁取向重构[106]和不同缺陷类型[125,126]等多种机制来解释实验和理论上的不一致,关于这方面的研究仍然需要未来进一步的探索.

图3 MnBi2Te4 块体和薄膜的基本表征 (a)磁化(沿着c 轴方向)和电阻随着温度变化曲线;(b)在2 K 温度下,厚度为4 SL 到8 SL 的薄膜的反射型磁圆二向色谱信号随着磁场的变化;(c)由拓扑表面态形成的线性狄拉克锥色散关系以及其在狄拉克点附近的放大图;图(a)和(c)来自文献[107],图(b)来自文献[110]Fig.3.Basic characterization of MnBi2Te4 bulk crystal and thin flakes: (a) Magnetization (with magnetic field applied along c axis)and resistance as functions of T;(b) reflective magnetic circular dichroism (RCMD) measurements as a function of magnetic field for 4 SL to 8 SL flakes at T=2 K;(c) linear band dispersion with a clear Dirac cone formed by surface states and the enlarged plot of the dispersion near the Dirac point;(a) and (c) are adopted from Ref.[107],(b) is adopted from Ref.[110].
3 磁性拓扑绝缘体中的量子输运和相变调控
3.1 磁性掺杂拓扑绝缘体
3.1.1 量子反常霍尔效应温度提升
自从在30 mK 极低温条件下的磁性掺杂拓扑绝缘体Cr-(Bi,Sb)2Te3中实现量子反常霍尔效应以来(如图4(a)—(c)所示),该领域一个重要的研究方向为优化量子反常霍尔效应并提升其量子化的实现温度.温度的提升不仅将降低量子反常霍尔效应在实验研究中的门槛,而且对于制备新型低功耗电子学器件具有重要应用价值.无序性被认为是限制量子反常霍尔效应温度的关键因素[41-48].从2015 年开始,研究者们针对这一问题开展了一系列谱学和成像的研究.美国布鲁海文国家实验室的Davis 研究组[41]利用扫描隧道显微镜对磁性掺杂拓扑绝缘体磁能隙的大小和空间分布开展研究,发现Cr 掺杂(Bi,Sb)2Te3样品中存在大量的磁性无序,这些无序会导致狄拉克点磁能隙的大小和分布在空间具有强烈的涨落.以色列威兹曼研究所Zeldov 研究组[42]利用扫描纳米超导量子干涉仪对Cr 掺杂(Bi,Sb)2Te3磁性拓扑绝缘体薄膜进行成像,首次观测到该体系在纳米尺度上存在超顺磁结构,发现磁无序会显著影响薄膜的输运和相变行为.因此从实验上降低无序被认为是实现高温量子反常霍尔效应的关键因素.美国麻省理工学院Moodera 研究组[38]提出在(Bi,Sb)2Te3拓扑绝缘体中掺杂具有更强磁各向异性的V 元素来优化量子反常霍尔效应,他们在实验中发现V 掺杂拓扑绝缘体确实会表现出更大的矫顽场,纵向输运上也表现出更低的纵向电阻,然而其反常霍尔电阻量子化的温度仍然小于100 mK.随后,日本东京大学Tokura研究组[39]借鉴二维电子气中的调制掺杂方法,将原先均匀体态掺杂的方式调整为分层掺杂,制备出“非磁-磁性-非磁-磁性-非磁”这种5 层拓扑绝缘体结构,实现了300 mK 温度下的完全量子化.2018 年,作者所在团队基于稀磁半导体领域中通过共掺杂提升磁均匀性的想法,提出在(Bi,Sb)2Te3拓扑绝缘体中同时掺杂Cr 和V 两种元素的方式,实现“1+1>2”的效果[40].如图3(d)—(f)所示,通过对Cr 和V 掺杂比例的精确调控,实验发现共同掺杂Cr 和V 能够将霍尔电阻量子化和纵向电阻消失的温度提升至300 mK,并且量子化霍尔电阻可以在超过50 V 的栅极电压范围得到保持,这一结果远大于此前Cr 掺杂拓扑绝缘体中的30 mK 量子化温度和5 V 的栅压范围.我们和美国Rutgers 大学吴伟达研究组合作,利用磁力显微镜成像的方法对单一掺杂和磁性共掺杂样品中进行成像,发现共掺杂样品中磁畴的大小和强度均高于单一掺杂样品.此外,不同于Zeldov 团队在Cr 掺杂样品发现的超顺磁现象,共掺杂样品在磁翻转过程中表现出典型的铁磁畴行为[43].这些发现都揭示了磁性共掺杂样品中量子化温度的提升主要来自于磁有序的增加.因此,选择不同的磁性掺杂元素组合,并结合调制掺杂方法,或许能在未来进一步提升量子反常霍尔效应的观测温度.

图4 磁性掺杂拓扑绝缘体中的量子反常霍尔效应 (a),(b) 5-QL 厚Cr0.15(Bi0.1Sb0.9)1.85Te3 中不同栅极电压下霍尔电阻率ρyx 和纵向电阻率ρxx 随着磁场的变化;(c)零磁场下霍尔电阻率ρyx(0)(蓝色空心方块)和纵向电阻率ρxx(0)(红色空心圆形)随栅压变化,以上数据在30 mK 温度下采集;(d),(e) 5-QL 厚(Cr0.16V0.84)0.19(Bi0.1Sb0.9)1.81Te3 在电荷中性点处霍尔电阻率ρyx 和纵向电阻率ρxx随着磁场的变化;(f)零磁场下霍尔电阻率ρyx(0)(蓝色实线)和纵向电阻率ρxx(0)(红色实线)随栅压变化,以上数据在300 mK 温度下采集.图(a)—(c)来自文献[35],图(d)—(f)来自文献[40]Fig.4.The optimization of the QAH effect in magnetically doped TIs.(a),(b) Magnetic field dependences of ρyx and ρxx at different Vg in a 5-QL Cr0.15(Bi0.1Sb0.9)1.85Te3 film;(c) dependence of ρyx(0) (empty blue squares) and ρxx(0) (empty red circles) on Vg,all the above data was measured at T=30 mK;(d),(e) magnetic field dependences of ρyx and ρxx at the charge neutrality point in a 5-QL (Cr0.16V0.84)0.19(Bi0.1Sb0.9)1.81Te3 thin film;(f) dependence of ρyx(0) (blue line) and ρxx(0) (red line) on Vg.All the data in the Crand V-codoped TI was measured at T=300 mK.(a)—(c) are adopted from Ref.[35],(d)—(f) are adopted Ref.[40].
3.1.2 磁无序引起的不同量子反常霍尔基态
由于量子反常霍尔效应发生在零磁场条件下,所以常常被简单地认为是一种零磁场版本的量子霍尔效应.然而,实现量子霍尔效应和量子反常霍尔效应的材料环境存在着截然不同的特征.前者实现于非常干净的二维电子气,器件迁移率可以轻松达到104cm2/(V·s)以上,而后者则是在磁性拓扑绝缘体中实现的,其迁移率极低,通常在100 cm2/(V·s)以下[86].此外,因为磁性是通过随机掺杂的方式引入的,量子反常霍尔效应样品中存在强烈的磁无序[41-43].无序一方面对量子反常霍尔效应温度的提升带来巨大挑战,另一方面也为探索新型拓扑物态和拓扑相变现象带来新的机遇.20 世纪90 年代,Kivelson 等[127]基于Chern-Simons 理论,提出了量子霍尔系统中的全局相图(global phase diagram),发现磁场和无序可以在二维电子气中产生量子霍尔液体和霍尔绝缘体两种不同量子基态,相关结果很快被崔琦等[128-131]在实验上证实.作为一个零磁场版本的量子霍尔效应,量子反常霍尔体系中是否存在类似的量子基态一直没有一个明确答案.不同于二维电子气中的非磁无序可以通过栅压进行调控,磁性拓扑绝缘体中的磁无序是掺杂过程中随机引入的,难以原位调控.同时,由于量子反常霍尔效应本身对生长条件敏感,进一步增加了调控无序的难度,因此过去几年实验方面的进展一直比较缓慢.
2020 年,作者所在团队[77]利用分子束外延方法在类似的条件下生长了82 块磁性掺杂拓扑绝缘体薄膜,实现了对不同磁无序区间的覆盖,从统计学角度有效解决了调节无序程度的实验难题.通过对每一块样品在不同温度、栅极电压下的电磁输运性质进行系统性测量,我们发现磁无序会在磁性拓扑绝缘体薄膜中引起此前未被认识到的新输运现象和量子基态.我们类比量子霍尔效应体系中用纵向电阻率表征无序[127-131],发现随着无序强度的增加,磁性拓扑绝缘体会从此前人们已知的量子反常霍尔相转变为一类被称为反常霍尔绝缘相的新基态,而这两种基态分别对应二维电子气中的量子霍尔液体和霍尔绝缘体.其输运行为如图5(a),(b)所示,在低无序的量子反常霍尔相中,随着温度趋向于绝对零度时,零磁场下纵向电阻率会趋向于零(~0),霍尔电阻率趋向于量子化(~h/e2),这与人们对量子反常霍尔效应中无耗散边缘态输运的认识一致.在高无序反常霍尔绝缘相样品中,研究发现其零磁场下纵向电阻率会随着温度降低呈现发散行为,同时霍尔电阻率依然保持很大数值甚至趋于量子化.更令人意外的是,在低无序量子反常霍尔相磁畴翻转的位置(矫顽场HC),纵向电阻率ρxx也会进入量子化~h/e2,并且随着温度的降低一直保持(如图5(a)中虚线所示),这种纵向电阻量子化的现象在此前量子霍尔效应和量子反常霍尔效应的研究中都鲜有报道.图5(c)总结了来自82 块样品的峰值纵向电阻率随着零磁场纵向电阻率的演化关系,趋于h/e2的行为清晰地表明磁无序会引起不同量子反常霍尔基态.在该工作中我们还研究了不同量子基态在磁场下的相变行为,如图5(d)和图5(e)所示,磁场的增加会压制磁无序,从而引起反常霍尔绝缘相到量子反常霍尔相的拓扑相变,不同温度下纵向电阻率ρxx会在磁场下交于一点.标度行为分析表明这种量子反常霍尔系统相变的临界电阻(2.6h/e2)和临界指数(0.31)均与传统量子霍尔效应相变存在显著差异[129-131].除了本项研究,国际上多个研究组在关于量子反常霍尔体系相变的实验也发现了和传统量子霍尔平台相变不一致的行为[67,132-134].

图5 磁无序引起的不同量子反常霍尔基态 (a),(b)处于量子反常霍尔相和反常霍尔绝缘体相的两块磁性掺杂拓扑绝缘体的霍尔电阻率ρyx 和纵向电阻率ρxx 随着磁场的变化,两块样品的化学组成分别是(Cr0.16V0.84)0.19(Bi0.1Sb0.9)1.81Te3 和Cr0.23(Bi0.4Sb0.6)1.77Te3;(c)从82 块样品中总结出的峰值纵向电阻率 和零磁场纵向电阻率 之间的关系;(d)处于反常霍尔绝缘体相的样品在不同温度下ρxx 随磁场变化曲线;(e)从图(d)中提取出的不同磁场下ρxx 随着温度的演化;(f)量子临界点附近关于ρxx 的标度行为分析.当临界指数κ 取0.31 时所有数据都重合在一条曲线上.图片来自文献[77]Fig.5.Distinct QAH ground states induced by magnetic disorder: (a),(b) Magnetic field dependent ρyx and ρxx for magnetically doped TIs in the ground states of QAH state and the AH insulator state,respectively,the chemical compositions of the two magnetically doped TIs are (Cr0.16V0.84)0.19(Bi0.1Sb0.9)1.81Te3 and Cr0.23(Bi0.4Sb0.6)1.77Te3;(c) relationship between peak value of longitudinal resistivity and zero field longitudinal resistivity summarized from the transport results of 82 magnetic TIs;(d) magnetic field dependent ρxx at different T in an AH insulator sample;(e) T-dependent ρxx extracted from (d) at different magnetic fields;(f) finite size scaling analysis of ρxx in the vicinity of the quantum critical point,all the curves collapse together for the critical exponent κ~0.31.The figures are adopted from Ref.[77].
目前实验上大部分关于量子反常霍尔效应的研究更多关注于低无序的量子反常霍尔相,对于处于高无序相样品的本质及其可能产生的物理效应的研究相对较少,关于这方面的探索不仅是当前量子物理研究的新的前沿,也是未来实现高质量原型器件构筑的关键.近年来,理论上在这方面的研究取得了许多进展,例如北京大学谢心澄团队[46]考虑磁无序和空间反演对称性,提出了量子反常霍尔平台相变过程可能会遵循BKT 相变机制.美国加州理工大学Alicea 团队[47]考虑磁性无序和反射对称性,发现无序会引起一类名为量子反常宇称霍尔相的新型拓扑物态,并提出可以通过测量量子化电导的方式对其进行探测.此外,除了关于磁性拓扑绝缘体本身无序性问题的讨论,在其组成的异质结中的无序性问题也受到广泛关注,特别是近年来关于能否利用量子反常霍尔薄膜-超导体异质结实现手征马约拉纳边缘模的实验在国际上引起了广泛的争议[135].例如马里兰大学Sau 研究组[136]和美国麻省理工学院文小刚研究组[137]分别从理论上提出,无序性引起的边缘态渗流和Andreev 反射机制可以给出非马约拉纳机制引起的类似实验现象,然而斯坦福大学的张首晟团队[138,139]的理论计算则表明,即使存在无序也不会影响马约拉纳费米子的出现.因此,对磁性拓扑绝缘体薄膜进行分类,明确样品的无序度,确定量子反常霍尔态在相图中的位置,对于寻找马约拉纳边缘模,探索基于手性边缘态的拓扑量子计算具有重要意义[140].
3.1.3 双手性反常霍尔效应
在磁性掺杂拓扑绝缘体的研究中,调节掺杂元素的类型和浓度,除了会改变磁有序的形成机制[31-34,88],还会引起反常霍尔效应手性的变化[141].如图6(a)和图6(b)所示,Cr 掺杂Bi2Te3磁性拓扑绝缘体的反常霍尔效应回滞在磁场下形成逆时针的闭合曲线,对应于零磁场下正的反常霍尔电阻率(>0),而对于Mn 掺杂Bi2Te3磁性拓扑绝缘体,其霍尔效应回滞则会形成顺时针闭合曲线,对应于符号为负的反常霍尔电阻率(<0).因此,利用反常霍尔效应不同手性作为不同铁磁序形成的指纹,可以对不同的磁序形成机制进行追踪.作者所在团队通过调控磁性掺杂元素Cr 和Mn 的比例,研究了不同厚度磁性拓扑绝缘体(Bi0.9MnxCr0.1—x)2Te3的反常霍尔效应演化[141].我们发现在不同层厚下,随着掺杂浓度从x=0 增大为x=0.1 时,反常霍尔效应手性会从逆时针变为顺时针,然而在不同层厚下,手性转变的临界掺杂浓度却发生了变化.当厚度从8QL 减薄到6QL 时,临界掺杂浓度会从x=0.08 降低为x=0.07,这一改变意味着Mn 元素主导的手性在二维的情况下更容易得到体现.通过对每一块样品在不同栅极电压下输运行为的系统性测量,我们发现在掺杂临界点时,反常霍尔效应的手性可以被栅压调控,进一步证明了Mn 元素主导顺时针反常霍尔效应更容易在薄层样品中得到体现.这和Mn 掺杂体系中发现的表面态狄拉克电子传导的RKKY 磁性机制相吻合.通过进一步减薄样品的厚度,利用表面态之间的杂化效应对磁序的改变,我们还在4QL 样品中实现了反常霍尔效应之外的拓扑霍尔效应[69,142].由于反常霍尔效应手性与磁性在狄拉克点打开能隙的符号密切相关,我们提出一种与3d 轨道电子自旋排布相关的唯象模型解释了手性的起源(如图6(c),(d)所示).对于Mn2+而言,当巡游电子与局域磁矩发生交换相互作用时,只有与3d 轨道占据态电子自旋相反的电子可以和局域磁矩电子发生耦合,对于Cr3+而言,这种耦合则只能发生在自旋方向相同的电子之间,因此,Mn 掺杂和Cr 掺杂体系具有符号相反的内禀交换场.近期实验上在本征磁性拓扑绝缘体MnBi2Te4中成功实现了陈数C=—1 的量子化反常霍尔效应,这与Cr 掺杂(Bi,Sb)2Te3体系C=+1 的量子反常霍尔效应形成鲜明对比,直接证明了这两种体系相反的内禀交换场.理论方面,清华大学徐勇[143]团队开展了基于磁性拓扑绝缘体材料的第一性原理计算,发现了库仑交换相互作用是影响磁性拓扑材料反常霍尔效应手性的关键机制.这些进展拓展了人们对于拓扑量子物态新奇输运行为的认识和理解.基于不同手性的反常霍尔体系,理论上还提出通过构筑Mn 掺杂和Cr 掺杂Bi2Te3异质结,用于轴子动力学和拓扑磁电效应的探测[28].

图6 两种不同手性的反常霍尔效应 (a)具有逆时针手性的反常霍尔效应回滞曲线,当磁化方向为正时反常霍尔电阻率符号为“+”;(b)具有顺时针手性的反常霍尔效应回滞曲线,当磁化方向为正时反常霍尔电阻率 符号为“—”;(c),(d)不同磁性掺杂拓扑绝缘体中狄拉克点能隙打开示意图,对于Mn 掺杂体系,巡游电子自旋方向与Mn2+离子3d 轨道占据态电子自旋方向相反,对于Cr 掺杂体系,巡游电子自旋方向与Cr3+离子3d 轨道占据态电子自旋方向相同.图片来自文献[141]Fig.6.AH effect with different chirality: (a) AH effect hysteresis with counter-clockwise chirality,the AH resistivity is “+”when the magnetization is positive;(b) AH effect hysteresis with clockwise chirality,the AH resistivity is “—” when the magnetization is positive;(c),(d) schematic illustrations of the Dirac gap opening process in different magnetic TI systems,for Mndoped system,the spin of itinerant electrons is antiparallel to the spin of the 3d electrons in the occupied states in Mn2+ ions.Whereas for Cr-doped system,the spin of itinerant electrons is parallel to the spin of the 3d electrons in the occupied states in Cr3+ions.The figures are adopted from Ref.[141].
3.2 本征磁性拓扑绝缘体
如前所述,MnBi2Te4是一种新型的二维本征反铁磁拓扑绝缘体,它的发现在国际上引起广泛关注.理论预言,MnBi2Te4在零磁场时,取决于上下表面的相对磁化,会分别表现出量子反常霍尔相(奇数层)和轴子绝缘体相(偶数层)[52,74].在外磁场存在时,体态反平行排列的磁矩会被极化到与磁场相同方向,宇称-时间反演联合对称性(PT-symmetry)将被破坏,MnBi2Te4会进入外尔半金属相.随着维度从三维降至二维,沿c方向的量子尺寸效应会引起外尔半金属能带发展为一系列二维量子阱态,MnBi2Te4会进入由不同拓扑数表征的铁磁陈绝缘体相[52,55].在更强磁场下,轨道效应和自旋效应会在铁磁性MnBi2Te4中引起拓扑相变,并产生具有螺旋式边缘态的新型拓扑量子物态.尽管目前实验领域面临着单晶质量和器件制备的双重挑战,近年来研究者们在MnBi2Te4输运方面仍然取得许多重要进展.国际上已经有6 个团队在该体系中实现了量子化输运[56-58,78,81,110-112,144].本节将回顾这方面的主要进展.
3.2.1 零磁场奇数层MnBi2Te4中的量子反常霍尔效应
量子反常霍尔效应是拓扑物理领域中最受关注的拓扑物态之一,自从2013 年该效应在磁性掺杂拓扑绝缘体中被首次发现以来,人们一直在探索如何对量子反常霍尔效应进行优化.然而,受限于合金化和掺杂过程,磁性掺杂拓扑绝缘体中不可避免地存在着大量的无序,真实材料磁能隙对应的温度(100 mK)远小于系统的居里温度(20—30 K),这使得实验上往往要在极低温环境下才能观测到量子化现象.因此,想要利用无耗散手性边缘态开展基础研究和器件应用存在着巨大的挑战.二维本征磁性拓扑绝缘体MnBi2Te4的发现为实现高温量子反常霍尔效应提供了一个理想平台.由于MnBi2Te4具有严格的化学计量配比,因此不存在磁性掺杂引起的无序性问题,理论计算表明其磁能隙可以高达38 meV,有望在室温观测到量子反常霍尔效应[52].此外,MnBi2Te4层间较弱的范德瓦耳斯相互作用使得实验上可以通过机械剥离的方式获得薄层样品,不再依赖分子束外延的薄膜样品生长方法,大大降低了对其开展基础研究的技术壁垒.2020 年,复旦大学张远波研究组[56]利用氧化铝辅助解理的方法将MnBi2Te4单晶解理到5 SL,在1.4 K 观测到量子反常霍尔效应(如图7(a)和图7(b)所示),零磁场下霍尔电阻Ryx达到0.97h/e2,纵向电阻Rxx降至0.061h/e2.通过施加面外方向磁场,实验发现霍尔电阻量子化程度得到进一步提高,在2.5 T 时达到0.998h/e2.此外,实验还通过对Rxx在不同温度下的曲线进行拟合,发现不同磁场下的Rxx很好地满足Arrhenius 公式,揭示了热激发对量子反常霍尔态输运的影响.值得关注的是,实验发现该体系的能隙在磁场下呈现非单调变化(如图7(c)所示),当磁场超过8 T 时,能隙会随着磁场的增大而减小,这种行为表明C=—1 的量子反常霍尔相中的内禀磁交换场方向与外磁场相反,也预示着该体系在更高磁场下可能会出现新的拓扑物态演化行为.

图7 厚度为5-SL 的MnBi2Te4 样品中观测到的量子反常霍尔效应 (a),(b)在1.4 K 温度下霍尔电阻Ryx 和纵向电阻Rxx 随着磁场的变化曲线,在零磁场条件下,霍尔电阻达到0.97h/e2,纵向电阻降至0.061h/e2.在磁场超过2.5 T 条件下,量子化程度被提升至Ryx~0.998h/e2;(c)通过纵向电阻数值随1/T 变化的Arrhenius 拟合获得的能隙随着磁场的变化曲线.图片来自文献[56]Fig.7.QAH effect in a five-layer MnBi2Te4 flake: (a),(b) Magnetic field dependent Ryx and Rxx acquired at 1.4 K.Ryx reaches 0.97h/e2 concomitant with Rxx of 0.061h/e2 at zero magnetic field,under magnetic field above 2.5 T,the QAH quantization is improved to Ryx~0.998h/e2;(c) energy gap as a function of magnetic field extracted from fitting the Arrhenius plots of Rxx as a function of 1/T.The figures are adopted from Ref.[56].
3.2.2 零磁场偶数层MnBi2Te4中的轴子绝缘体相
轴子绝缘体是凝聚态物理领域中另一类受到广泛关注的拓扑量子物态,其物理概念最初起源于高能物理中的粒子“轴子”,后者被视为暗物质的重要候选者之一[22,23].由于描述拓扑绝缘体磁电耦合项方程与高能物理中描述轴子动力学的方程的物理形式一致,实验上通过在拓扑绝缘体上下表面破坏时间反演对称性并打开符号相反的能隙,可以实现一种被称为轴子绝缘体的新型拓扑物态[15,24].理论预言,轴子绝缘体相不仅可以作为研究拓扑磁电效应的理想平台[70-72,93],还可以被应用于高能物理进行暗物质的探测[145-147].因此在拓扑绝缘体诞生之后,实现轴子绝缘体相就成为实验领域的一个重要目标.由于轴子绝缘体上下表面会携带符号相反的半整数量子霍尔电导σxy=(1/2)e2/h,因此观测到零级霍尔平台被认为是轴子绝缘体相存在的重要证据.2017 年日本东京大学Tokura 团队[70,71]通过生长具有不同矫顽场的磁性掺杂拓扑绝缘体异质结,首次在实现了轴子绝缘体相.随后美国宾州州立大学常翠祖团队[72]结合磁力显微成像技术,对该体系中的轴子绝缘体相的磁结构和电输运性质进行了进一步验证.然而,此前这些实现轴子绝缘体相的方案非常依赖于分子束外延生长过程中的精细调控,同时需要100 mK 以下的极低温环境和外磁场的辅助,此外,掺杂还会在样品中引入大量无序.因此在过去几年里,轴子绝缘体领域的发展受到强烈制约.MnBi2Te4的发现则为实现轴子绝缘体相提供了一个极佳的平台,其层状A 型反铁磁结构使得偶数层MnBi2Te4在零磁场下自动满足轴子绝缘体的实现条件.
2020 年作者所在团队通过机械剥离的方法将MnBi2Te4单晶解理到6SL,首次在MnBi2Te4体系中观测到轴子绝缘体相,通过施加面外磁场,还实现了轴子绝缘体到陈绝缘体的拓扑相变[57].如图8(a)所示,随着磁构型在反铁磁态和铁磁态之间的转换,MnBi2Te4在磁场下展现出丰富的输运特性,霍尔电阻率ρyx和纵向电阻率ρxx表现出一系列与层间磁性翻转相关的跳变行为[144].特别是当费米能级被调至带隙中间时(蓝色框架),MnBi2Te4会进入轴子绝缘体相存在的区间,在低磁场反铁磁态,样品在1.6 K 温度下纵向电阻率ρxx达到6h/e2,同时霍尔电阻率ρyx表现出很宽的零级霍尔平台.随着磁场增大,反铁磁态被极化为铁磁态,MnBi2Te4进入陈数C=—1 的铁磁陈绝缘体相,其纵向电阻率ρxx降至0.018h/e2,霍尔电阻率ρyx达到0.974h/e2.除了在磁场下展现出量子化霍尔平台外,不同磁场下的霍尔电阻率在栅压下也表现出清晰的量子化平台(图8(b)—(d)).在该工作中我们还通过标度分析,对反铁磁轴子绝缘体相和铁磁陈绝缘体相之间的临界行为进行拟合,发现这两种拓扑物态之间的量子相变行为和二十年前崔琦等[131]在量子霍尔系统中发现的量子霍尔液体到霍尔绝缘体的相变满足同样的临界电阻和临界指数.相比于此前研究者们在掺杂拓扑绝缘体中实现轴子绝缘体相的方案,在MnBi2Te4中实现轴子绝缘体器件制备方法简单,无需外磁场,同时观测温度提高了一个数量级.近期,美国哈佛大学许苏阳团队[79,81]通过电场调控,观测到偶数层MnBi2Te4中的层霍尔效应[81],并且他们还利用光学方法测量到了偶数层MnBi2Te4中的轴子动力学,进一步证实了零磁场下的轴子绝缘体相[79].

图8 厚度为6-SL 的MnBi2Te4 在不同电压下的输运行为 (a),(b)在1.6 K 温度时不同栅压下霍尔电阻率ρyx 和纵向电阻率ρxx随着磁场的变化曲线,当费米能级被调节到带隙中时(22 V≤Vg≤30 V,如蓝色区间所示),零磁场巨大的纵向电阻率和很宽的零级霍尔平台揭示了轴子绝缘相存在的重要证据,在高磁场下,量子化的霍尔电阻平台和消失的纵向电阻率表明系统进入陈绝缘体相;(b)零磁场纵向电阻率ρxx 和霍尔电阻率ρyx 在磁场下的斜率随着栅极电压变化图;(c) 磁场—9 T 时纵向电阻率ρxx 和霍尔电阻率ρyx 随着栅极电压变化图;(d)轴子绝缘体相和陈绝缘体相磁结构和电子结构示意图.图片来自文献[57]Fig.8.Gate dependent transport properties in a six-layer MnBi2Te4: (a) Magnetic field dependence of ρyx and ρxx at different gate voltages at T=1.6 K,when Fermi level EF lies within the band gap for 22 V ≤Vg≤30 V (blue square envelope),both the large longitudinal resistivity ρxx and wide zero Hall plateau are key signatures of the axion insulator state,at high magnetic field,the nearly quantized Hall plateau and vanishing ρxx are characteristics of a Chern insulator;(b) the Vg dependence of ρxx and the slope of ρyx vs.H measured at T=1.6 K around zero magnetic field;(c) the evolution of ρxx and ρyx as a function Vg at T=1.6 K andµ0H=—9 T,which reveals the Chern insulator state;(d) the schematic pictures of the magnetic order and electronic structure of the axion insulator and Chern insulator state.The figures are adopted from Ref.[57].
3.2.3 高磁场少层MnBi2Te4中不同陈数陈绝缘体相
除了在零磁场下不同奇偶性层厚的MnBi2Te4是量子反常霍尔相和轴子绝缘体相之外,第一性原理计算还发现,磁场极化后的MnBi2Te4是理想的第二类外尔半金属,并且只在费米能级附近存在一对外尔点[52,55,61].因此通过减薄厚度,降低维度,沿c轴方向的量子尺寸效应会导致外尔半金属体能带劈裂成一系列分立的量子阱态.实验上有机会在少层MnBi2Te4薄膜中看到具有不同陈数的陈绝缘体相.北京大学王健研究组[58]测量了厚度为10 SL 的MnBi2Te4器件在磁场下的输运性质,如图9(a),(b)所示,他们发现当磁场强度超过10 T时,霍尔电阻Ryx会量子化在—0.5h/e2,并且纵向电阻Rxx消失,这种半整数量子霍尔电阻对应着体系具有更高的陈数C=—2,同时意味着在实空间存在两支手性边缘态承载输运.除了通过改变层厚实现高陈数外,美国华盛顿大学许晓栋团队[111]通过电场调控空间反演对称性和载流子浓度,在50 mK极低温下也观察到了高陈数现象.如图9(c)—(h)所示,他们发现在特定载流子浓度n2下,随着磁场增大,MnBi2Te4首先会在4 T 左右由反铁磁态进入倾斜反铁磁态(canted-AFM),霍尔电阻率ρyx表现出量子化—h/e2的平台,同时纵向电阻率ρxx明显下降.当磁场增大到10 T 左右,倾斜反铁磁态被完全磁化,霍尔电阻率ρyx从—h/e2变为—0.5h/e2,纵向电阻率ρxx降至极小,这标志着体系进入了一个具有高陈数C=—2 的拓扑态,这种载流子浓度调控下陈数的变化意味着除了原本拓扑能带的贡献,朗道能级引起的量子霍尔态也可能会贡献输运.理论方面,北京大学谢心澄团队[148]考虑MnBi2Te4中的无序性,提出安德森局域化机制可能会引起磁场下量子霍尔效应和量子反常霍尔效应共存的现象,为MnBi2Te4中高陈数量子化现象提供了另外一种可能的解释.

图9 磁场极化的铁磁MnBi2Te4 中高陈数量子化现象 (a),(b)厚度为10-SL 样品在2—15 K 条件下霍尔电阻Ryx 和纵向电阻Rxx 随着磁场的变化.在温度为13 K 时霍尔电阻Ryx 可以达到0.97h/e2;(c)—(e)厚度为7-SL 的双栅极MnBi2Te4 器件在不同载流子浓度下n1—3 霍尔电阻率ρyx 随磁场的变化;(f)—(h)纵向电阻率ρxx 随磁场的变化,在载流子浓度为n2 时,超过10 T 的磁场可以引起了C=—2 的高陈数的量子化现象,其霍尔电阻率ρyx 为0.5h/e2,纵向电阻率ρxx 为0.05h/e2.图(a)和(b)来自文献[58],图(c)—(h)来自文献[111]Fig.9.Chern insulator quantization with high Chern number in magnetic-field polarized FM MnBi2Te4: (a),(b) Ryx and Rxx as a function of magnetic field at different Ts from 2 K to 15 K in a 10-SL sample,the Hall quantization can reach 0.97h/e2 at 13 K;(c)—(e) ρyx as a function of magnetic field under varied carrier density n1—3 for a 7-SL dual gated MnBi2Te4 devices;(f)—(h) the according variation of ρxx as a function of magnetic field under different carrier density n1—3.A C=—2 state with ρyx=0.5h/e2 and ρxx=0.05h/e2 appears when magnetic field is increased to above 10 T for carrier density n2.(a) and (b) are adopted from Ref.[58].(c)—(h) are adopted from Ref.[111].
3.2.4 脉冲强磁场中MnBi2Te4陈绝缘体的物态演化
寻找新的拓扑量子物态一直是凝聚态物理研究的重要目标,以强磁场为代表的极端条件被认为是有机会产生新物理的强有力手段.2021 年,作者所在团队利用最高61.5 T 的脉冲强磁场,对少层MnBi2Te4在极端条件下的拓扑物态演化行为开展研究,发现了一类具有螺旋式边缘态输运的新型拓扑物态[78].我们首先通过机械剥离的方法在Si/SiO2衬底上解理出厚度为7 SL 的MnBi2Te4薄膜,并通过电子束曝光的方法将MnBi2Te4薄膜制备成场效应管器件,低场输运测量表明其迁移率达到目前报道的磁性拓扑绝缘体薄膜的最高值,在电子型和空穴型一侧分别达到3114 和2098 cm2/(V·s).在此器件中,我们开展了不同栅极电压调控的脉冲强磁场输运测量,图10(a)展示了当费米能级调至能隙附近时强磁场下的输运行为,实验发现在低磁场(10 T 左右)MnBi2Te4首先进入铁磁陈绝缘体相,在输运上表现出量子化霍尔电阻Ryx=—h/e2和消失的纵向电阻Rxx=0.随着磁场增大到30 T,我们意外地发现陈绝缘体相量子化霍尔平台被压制到一个零级平台Ryx=0,同时原本消失的纵向电阻在磁场下迅速升高,并在半整数量子电阻Rxx=0.5h/e2的位置形成了一个平台,如图10(a)虚线所示.随着磁场进一步增加到61.5 T,零级霍尔平台一直保持到最高场,而Rxx继续升高到6h/e2.值得关注的是,不同于普通绝缘体中零霍尔电导平台σxy=0 可能来自张量关系和发散的纵向电阻率ρxx,在输运上直接观测到霍尔电阻Ryx=0 的平台是非常罕见的,同时与之相伴的半整数量子化纵向电阻Rxx=0.5h/e2也预示着背后可能存在拓扑非平庸的物理.在此前量子自旋霍尔效应螺旋式边缘态输运的实验中曾经看到类似的迹象,但是无论是霍尔电阻Ryx零平台还是纵向电阻Rxx量子化程度都明显弱于强场下的数据[149-152].结合第一性原理计算,我们发现铁磁态MnBi2Te4陈绝缘体相的输运主要由费米能级以下陈数C=—1 的能带贡献,在实空间对应一支拓扑保护的手性边缘态.在强磁场作用下,费米能级附近不同自旋极化的量子阱态会在塞曼效应作用下沿相反方向移动,两支原本不贡献输运的拓扑平庸能带会发生能带反转,产生一支陈数C=+1 的新拓扑能带.因此,在与原本铁磁性引起的C=—1拓扑能带的共同作用下,MnBi2Te4在强磁场下的输运由两支运动方向相反的螺旋式边缘态贡献,其能带结构和边缘态演化示意图如图10(b),(c)所示.为了进一步验证强磁场下的零级霍尔平台是由螺旋式边缘态贡献的,我们分别测量了两端法、三端法和不同构型下的非定域输运 (nonlocal transport),得到了一系列与螺旋式边缘态Landauer-Büttiker 公式预言一致的分数量子电阻(如图10(d)所示).不同于传统二维电子气中整数量子霍尔平台数值在磁场下会继续增大并进入分数态,我们发现MnBi2Te4陈绝缘体相的量子化霍尔平台在磁场下会被压制到零,这种以零级霍尔平台和量子化纵向电阻为特征的输运现象,代表着强磁场下出现了一类破缺了时间反演对称性的螺旋式陈绝缘体相.

图10 磁场在MnBi2Te4 陈绝缘体相中引起的C=0 的螺旋式拓扑态 (a)栅压在1—6 V 之间时纵向电阻Rxx 和霍尔电阻Ryx 随磁场变化曲线,栅压为4 V 时,30 T 的磁场使C=—1 陈绝缘体相被完全压制,并引起一个以极宽零级霍尔平台为主要特征的C=0 态,黑色虚线标注了零级平台出现位置时纵向电阻上的半整数量子化现象;(b)强磁场下塞曼效应引起的能带反转以及能带结构演化示意图;(c)在磁场引起的C=—1 到C=0 拓扑相变过程中边缘态演化情况;(d)不同测量构型下的两端输运、三端输运以及非定域输运测量结果,其中插图描述了不同的测量构型示意图,玫红色虚线标记了由Landauer Büttiker 公式预言的螺旋式边缘态贡献的量子化电阻数值.图片来自文献[78]Fig.10.Magnetic field driven helical state with C=0 in a MnBi2Te4 Chern insulator: (a) Magnetic field dependent longitudinal resistance Rxx and Hall resistance Ryx at 1 V≤Vg≤6 V,at Vg=4 V,the C=—1 state is completely suppressed when magnetic field is increased to above 30 T,followed by the C=0 state characterized with a broad zero Hall plateau,the black dashed line denotes the half-quantized plateau of Rxx=0.5h/e2;(b) schematic illustration of the electronic band structure evolution in strong magnetic field with Zeeman-effect-induced band inversion;(c) the evolution of edge states in the magnetic field driven topological phase transition between C=—1 and C=0 phase;(d) two-,three-terminal,and nonlocal measurements in various configurations,the insets display the schematic layouts of the experimental setup,the expected quantized values for R2T,R3T,and RNL derived from the Landauer Büttiker formalisms for helical edge transport are denoted by the broken magenta lines.The figures are adopted from Ref.[78].
4 总结与展望
本文主要对磁性拓扑绝缘体领域近年来在拓扑物相和拓扑相变方面的重要进展进行了回顾,特别关注了作者所在团队近期在量子输运实验方面所取得的研究成果.文中详细介绍了量子反常霍尔效应、轴子绝缘体相和陈绝缘体相等新奇拓扑物态的构筑与调控.然而,由于篇幅所限,本文并未能全面覆盖该领域的全部重要研究成果.
尽管磁性拓扑绝缘体领域已有十年的发展历程,针对这类体系的研究仍在蓬勃展开.近年来,随着一系列重要基础科学成果的不断涌现,以及国内外制备新型拓扑电子学器件的战略需求不断升温,磁性拓扑绝缘体领域依然有许多重要科学问题亟待深入研究.例如,近期日本东京大学Tokura团队[82]在半磁拓扑绝缘体中观测到半整数量子霍尔电导,作者所在团队[124]在MnBi2Te4轴子绝缘体相中观察到巨大的非定域边缘态输运信号,这些最新的实验进展引起了理论上很多关于磁性拓扑绝缘体中半整数量子化输运现象的热烈讨论[153-158],实验方面如何对这种无相互作用体系中出现的分数量子化现象进行有效探测和调控,是否能够在输运中成功测量到半整数量子化边缘电流,以及如何在实验上测量到量子化拓扑磁电耦合系数,都是目前尚未解决的重要科学问题.同时,拓扑体系与其他自由度相互作用产生的新效应也是目前拓扑物理研究的前沿课题之一,例如在无序作用下安德森局域化对拓扑体系相图的拓展[148,159],磁性量子相变和拓扑相变的耦合对量子霍尔平台相变普适类和动力学性质的影响[42,77,160],磁性拓扑绝缘体在超导近邻作用下产生马约拉纳边缘模的探测与非阿贝尔编织[135,138,140],强磁场、超高压和极低温等极端条件下拓扑量子物态的演化[151,152,161-163],以及转角MnBi2Te4中可能存在的平带现象和关联效应等[164].当前,关于二维本征磁性拓扑绝缘体的研究正处于起始阶段,MnBi2Te4作为实验上发现的第一个同时具备二维特性、本征磁性和能带拓扑的新型量子材料,仍是目前拓扑物理领域研究最多的材料之一.然而Mn-Bi-Te 家族中除了MnBi2Te4相之外,还存在许多具有不同拓扑性和磁结构的其他成员,例如MnBi4Te7,MnBi6Te10和MnBi8Te13等[103],这些材料同样具有巨大的研究潜力.在应用方面,提高实验上量子反常霍尔效应的观测温度,开发基于无耗散手性边缘态的新型电子学器件等问题,仍是目前极具挑战性的研究方向.因此,在未来的研究中,需要继续寻找新型二维磁性材料和拓扑材料,积极探索高质量的器件制备方法和调控技术,深入研究其拓扑量子物性,这不仅将有助于解决上述重大科学问题,还将推动拓扑物理领域的进一步发展.

