马约拉纳零能模的输运探测*

徐磊 李沛岭 吕昭征 沈洁3) 屈凡明3)4) 刘广同3)4)† 吕力3)4)

1) (中国科学院物理研究所,北京凝聚态物理国家研究中心,北京 100190)

2) (中国科学院大学物理科学学院,北京 100049)

3) (松山湖材料实验室,东莞 523000)

4) (合肥国家实验室,合肥 230000)

理论预言拓扑超导体能够承载服从非阿贝尔统计的伊辛任意子—马约拉纳零能模,因而可用于实现容错的拓扑量子计算,是凝聚态领域最受关注的前沿课题之一.本文重点回顾了电学输运手段在研究马约拉纳零能模中的应用.在简要介绍拓扑超导、马约拉纳零能模和非阿贝尔统计等基本概念的基础上,对当前实现拓扑超导的多种方案进行了总结.重点介绍了利用低温输运手段探测马约拉纳零能模的实验方法,涵盖了超导/纳米线中广泛使用的电子隧穿谱、库仑阻塞谱和非局域电导探测,以及约瑟夫森器件中使用的(逆)交流约瑟夫森效应探测和电流(能量)相位关系的探测.同时,对利用上述测量手段得到的实验结果可能存在的平庸解释进行了必要的补充和说明.最后对马约拉纳零能模的输运探测进行了总结与展望.

1 引言

自1980 年von Klitzing[1]发现整数量子霍尔效应 (integer quantum Hall effect,IQHE) 以来,研究者们在凝聚态物质中陆续发现了多种和能带拓扑相关的材料体系,包括拓扑绝缘体、拓扑半金属和拓扑超导体.在这些体系中,体能带的拓扑性导致在边界处存在无能隙的边缘态[2].而在拓扑超导体中,凭借无能隙的边缘态和超导本身的粒子空穴对称性,在边界处 (涡旋中心) 支持一种被称作马约拉纳零能模 (Majorana zero mode,MZM) 的准粒子,它的反粒子是其自身.MZM 是伊辛 (Ising)任意子,遵从非阿贝尔统计规律,对组成系统的粒子进行交换操作是非对易的,系统的多体状态强烈地依赖于交换操作过程[3-6].利用MZM 的这一特殊性质,构造受拓扑保护的高容错的拓扑量子比特成为可能,对其进行编织和融合可以实现构建通用量子计算机的基本量子门,这已经成为实现通用量子计算最有前景的方向之一[7,8].

鉴于利用MZM 构建量子比特的诸多优势,已经提出多种基于MZM 的编织方案[9-14].在物理上实现拓扑量子比特之前,首先要从实验上确认MZM的存在.当前正处于实现拓扑量子比特物理的关键时期,亟需从实验上确认MZM 的存在.目前,理论上关于寻找拓扑超导、探测MZM 的方案已经十分成熟[15-32],实验上在多种体系中的确观察到了符合理论预期的信号.例如,人们已经在本征拓扑超导体系 (FeSe0.45Te0.55[33-36],CuxBi2Se3[37])、超导/半导体纳米线 (InAs[38-46],InSb[47-54])、超导/拓扑绝缘体 (Bi2Te3[55,56],Bi2Se3[57],HgTe[58]) 及磁性原子链[59-61]等体系中观察到了零偏压电导峰 (zero-bias conductance peak,ZBCP) 以及分数约瑟夫森效应[62-71].尽管如此,上述现象仍然无法排除平庸机制的解释[72-88].因此,实验上需要给出更加确凿的实验证据,以确保这些信号的确来源于MZM.本文着重回顾了当前利用输运实验手段探测MZM的多种实验方案,包括电子隧穿谱、库仑阻塞谱、非局域电导谱、(逆)交流约瑟夫森效应探测和电流(能量)相位关系探测方案等,并对其中可能由平庸机制引入的信号进行了必要的讨论.

2 拓扑超导和马约拉纳零能模

2.1 拓扑超导

拓扑本身是一个数学概念,它描述的是物体连续形变之后保持不变的性质;在凝聚态物理中,一个系统的哈密顿量在不关闭能隙的情况下发生连续变换,也不改变其“拓扑性质”.这里的“拓扑性质”可以用拓扑不变量来表达,和数学中的拓扑有着相似的理念.譬如在最早发现的IQHE 里,Thouless 等[89]引入TKNN 不变量或陈数精确地表示量子化的霍尔电导,在系统的能隙不发生关闭和重新打开的过程时,这种量子化的电导平台总是稳定存在的.进一步的研究发现了量子自旋霍尔效应 (quantum spin Hall effect,QSHE) 的存在[90].与IQHE不同的是,它满足时间反演对称性,在体系的边缘存在着两支反向传播的螺旋态[91].这一体系由于时间反演对称性的保护,Kane 和Mele[91]引入了Z2拓扑数.Z2=0 对应常规的绝缘体,Z2=1 则对应具有QSHE 的二维拓扑绝缘体[92].在三维体系中,这一结果可以推广到4 个Z2拓扑不变量构成的新拓扑不变量(v0,v1,v2,v3),其中v0与第三维紧密相关,借此可以将三维拓扑绝缘体区分为强拓扑和弱拓扑绝缘体[92-94].

与拓扑绝缘体的分类方法类似,拓扑超导体也可以根据其固有的粒子空穴对称性与其他对称性进行分类,见表1 所列.图1 展示了在二维情况下,IQHE 和QSHE 与拓扑超导之间的类比关系[95].时间反演对称破缺的手性拓扑超导具有和IQHE 相似的手性边缘态,而具有时间反演对称性的螺旋拓扑超导则与QSHE 类似,拥有反向传播的两支边缘态.人们对拓扑超导的关注来源于其本身具有的一些奇异性质,其中最重要的是它支持具有非阿贝尔统计性质的MZM[6],这是它能用于拓扑量子计算的主要物理依据;另外,也有研究指出在拓扑超导体系中经历特定的量子相变可以在凝聚态体系中实现超对称[96].

表1 超导体的对称性和相应的拓扑不变量[7]Table 1.Symmetries and corresponding topological invariants of superconductors[7].

图1 二维手性拓扑超导和IQHE、二维螺旋拓扑超导和QSHE的对比示意图 (a) 二维手性拓扑超导和IQHE 的对比示意图,在这两个系统中,时间反演对称性破缺,其边缘态具有确定的手性;(b) 二维螺旋拓扑超导和QSHE的对比示意图,这两个系统都有时间反演对称性和无能隙的螺旋边缘态,在同一边缘上不同自旋极化的电子传播方向相反.图中虚线表明拓扑超导体的边缘态是马约拉纳费米子,其准粒子能谱中E＜0 的部分是冗余的,引自文献[95]Fig.1.Schematic comparison of two-dimensional chiral topological superconductor (TSC),IQHE,two-dimensional helical TSC and QSHE.(a) Schematic comparison of twodimensional chiral TSC and IQHE state.In both systems,time reversal symmetry is broken,and the edge states have a definite chirality.(b) Schematic comparison of two-dimensional time reversal invariant TSC and QSHE.Both systems maintain time reversal symmetry and have a helical pair of edge states,where opposite spin states counterpropagate.The dashed lines indicates that the edge states of the topological superconductors are Majorana fermions so that the E＜0 part of the quasi-particle spectra are redundant,adapted from Ref.[95].

2.2 马约拉纳零能模

1937 年,意大利物理学家埃托雷·马约拉纳(Ettore Majorana) 提出了Dirac 方程的一组实数解[97],使得场算符ψ=ψ*,这意味着这个解对应的粒子具有一个奇异的性质,即其反粒子就是它本身,因此这种粒子被称为马约拉纳费米子.最初在粒子物理领域,中微子被认为是马约拉纳费米子的最佳候选,但是直到目前仍然没有确定的结论[98].在凝聚态物理领域,丰富的准粒子激发为探究马约拉纳费米子提供了很好的平台.如果电子的产生(湮灭) 算符为c†(c),可以构造如下两个算符:

结果显示，吸烟成瘾组的男性比例高于其他两组，网络成瘾组的女性比例高于其他两组(χ2=29.066，P＜0.05)，3组被试在性别上差异有统计学意义。但在年级、民族、是否为独生子女以及家庭所在地上比较，差异均无统计学意义(P＞0.05)。见表1。

根据Kitaev 的一维p 波超导模型,在这个体系中将会出现4π 周期的约瑟夫森电流[189].这个结论对其他拓扑超导体系也适用,并得到了相应实验的支持.在常规超导体和拓扑超导体构成的约瑟夫森结中,其能量和相位的关系可分别表达为[188]:

2.3 非阿贝尔统计

MZM 遵从非阿贝尔统计规律,这意味着粒子交换操作在这个系统中是不对易的.这种性质在拓扑超导体系中普遍成立,它不依赖于具体的实现方式及MZM 局域的位置,如涡旋中心或者是纳米线的两端[6,101,102].

首先考虑只有两个MZMs (γ1,γ2)的情况,利用(1) 式可以构造单个费米子的产生和湮灭算符:.其对应的占据数可以取0 和1 两个值,这意味着由一对MZMs 组成的系统只能是两重简并的,在粒子数表象下可以分别写作|0〉,|1〉.当把这个结论推广到2N对MZMs 的系统,可以得到整个系统的简并度为2N.在由这些粒子张成的空间中,可以继续讨论它们的交换操作.理论上给出任意两个MZMs 的交换算符为[6]

其表示两个MZMs 逆时针交换一次所经过的变换(顺时针交换时,(2)式中的负号变为正号,后续讨论采用(2)式).利用(1)式可以得到马约拉纳算符的反对易关系:

由此可以得到当γi与γj交换一次后的变换规则如下:

仍然考虑只有两个MZM 的情况,假如γ1绕着γ2逆时针交换一次 (如图2(a) 所示),那么系统的状态将发生如下变换:

图2 MZMs 非阿贝尔统计原理示意图 (a) γ1 环绕 γ2逆时针旋转半圈;(b) γ1 环绕 γ3 逆时针旋转1 圈;(c) 对两对MZMs 进行编织操作的示意图Fig.2.Schematic of the non-Abelian statistics principle of MZMs: (a) γ1 winds counterclockwise around γ2 by half a turn;(b) γ1 winds counterclockwise around γ3 by one full turn;(c) schematic of braiding two pairs of MZMs.

显然在这个过程中只是积累了一个额外的相位,系统的状态并没有改变,所以这里的交换仍然是平庸的交换操作.为了实现非阿贝尔交换操作,这里需要再引入一对新的MZMs (γ3,γ4).显然,对于γ1,γ2(γ3,γ4) 之间的交换操作并不会影响另外一对MZMs 的操作,所以这里只需考察γ1,γ3之间的交换 (其余操作可类似得到).为方便起见,这里引入逻辑比特的计算基,用以表示单个量子比特,它们张成的子空间可以由本征方程-γ1γ2γ3γ4|ψ〉=|ψ〉确定[103].在计算基下,马约拉纳算符和泡利矩阵之间的关系为:σx=-iγ2γ3,σy=-iγ1γ3,σz=-iγ1γ2.现在进行如图2(b) 所示的操作,γ1绕γ3逆时针旋转一圈,这个过程相当于γ1和γ3交换了两次,其演化算符(U13)2=-γ1γ3=-iσy,这个过程中系统状态的变化即为

显然,该操作不仅会附加额外的相位,而且还会直接改变系统所处的状态,这正是非阿贝尔统计的奇异性质,图2(c) 所示的时空图再现了这一编织过程.实际上,上述讨论中已经构建了单个的量子比特以及3 个泡利门,结合理论提出的其他基本量子门的实现方案,即可实现受拓扑保护的量子计算[104-112].

从编目员视角看，视频文件不仅是节目或电视作品，而是待开发的影像内容宝库，要从中寻找有价值的部分，标注有价值的节目、资料或空镜头。这种判断也是一种再创造。将电视作品分解还原，当编目员从标引视角审视这些内容时，能否从中提取有价值的东西关键还在于对内容价值的敏感性，这种敏感性要求编目员在进行著录标引的过程中，需要对资源全方位分析，敏锐地获取外表属性和内特征，并迅速判定其潜在的价值。

3 拓扑超导的实现

拓扑超导的实现和MZM 的探测是当前凝聚态物理领域的研究热点.经过十多年的研究,在本征拓扑超导以及人工拓扑超导研究方面都取得了丰硕的成果,现总结如下.

3.1 本征拓扑超导体

本征拓扑超导体的候选体系主要包括超导拓扑半金属、非中心对称超导体、重费米子超导体和铁基超导体等.

狄拉克半金属Au2Pb[113],在1.3 K 时出现超导[114],理论计算表明,它是具有自旋极化拓扑表面态的超导体,被认为是本征拓扑超导体的有力候选者.第二类外尔半金属TaIrTe4[115,116],在1.4 K 时显示出表面超导电性,低温扫描隧道谱 (scanning tunneling spectroscopy,STS) 以及低温输运实验均表明这个体系可能存在非常规的p 波超导电性[117].第二类外尔半金属Td-MoTe2[118-120],在100 mK 时显示出超导电性[121],并且在薄层器件中观察到了不同于正常夫郎禾费衍射的锯齿形图样,被认为起源于边缘超流,表明该体系可能是拓扑非平庸的外尔超导体[122].最近,在Se 掺杂样品中观察到了超导增强[123],利用点接触谱实验观察到了ZBCP[124],以及高压μ 子自旋旋转 (muon spin rotation,μSR)实验[125],均表明MoTe2具有两带超导的特性,可能是具有拓扑的s+-态的非常规超导体.

Li2(Pd1-xPtx)3B 与CePt3Si[126,127]均是非中心对称超导体,其超导能隙内存在线节点 (line nodes),可能具有混合的s+p 波超导成分[128].在富Pt 的Li2(Pd1-xPtx)3B 体系中,更高的p 波成分可能源于强自旋-轨道耦合作用 (spin orbital coupling,SOC)[129-131].UPt3是典型的重费米子超导体[132],核磁共振实验 (nuclear magnetic resonance,NMR)支持这一体系是自旋三重态配对的拓扑超导体[133].低温下UPt3有3 个超导相,分别是超导相A (0.48 K＜T＜0.53 K,低场),超导相B (T＜0.48 K,低场)和超导相C (T＜0.48 K,高场)[132].在超导相B中,已有实验给出了该体系时间反演对称破缺的实验证据[134-138].目前超导相B 被认为极有可能是自旋三重态配对的拓扑超导体.

通过表5可以看出，浮选尾矿熔炼合金经过真空蒸馏后，在1 000 ℃、蒸馏90 min的条件下，可以获得最优的金、银直收率，同时铅、铋、碲的脱除率均较高，但随着温度的升高，挥发率增加，虽然残留物中金、银的富集倍数增加了，但是直收率却大幅度下降，经济性有所下降。锑虽然在理论计算中拥有较高的脱除率，但在实际试验中脱除效果较差，可能源于浮选尾矿熔炼合金中锑并非以二元合金的形式存在，组分较为复杂，难以挥发。

铁基超导可以视作体内常规超导和表面拓扑超导形成的复合体系,当温度降到Tc以下,拓扑表面态将被体超导邻近.角分辩光电子能谱实验已经清晰观察到FeTe0.55Se0.45具有多种拓扑相,包括费米能级附近的拓扑绝缘体态[33,139]与本征费米能级以上的狄拉克半金属态[140-142].近来,STS 实验先后在FeTe0.55Se0.45的涡旋中心观察到ZBCP和接近量子化的ZBCP[33-35],并指出在具有MZM的涡旋处,其束缚态能级序列相对正常涡旋存在半整数能级嬗移[143].CaKFe4As4可以认为是由CaFe2As2和KFe2As2自发插层形成的[144],相比之下该体系更均匀,并具有更高的超导转变温度[145].实验上已经证实了CaKFe4As4中存在拓扑非平庸的狄拉克表面态,并且可观察到与MZM 相符的ZBCP 信号[146],这使其成为研究MZM 的理想平台.LiFeAs 是化学计量比的铁基超导体系[147],与FeTe0.55Se0.45类似,其在费米面附近也存在一个拓扑绝缘体狄拉克锥和一个拓扑狄拉克半金属狄拉克锥[148].令人振奋的是,应力在该体系中诱导出了大面积、高度有序和可调控的MZM 格点阵列[149],为实现拓扑量子计算提供了高质量研究平台.

需要说明的是,在上述材料中观测到了拓扑超导的某些特征,但仍需要更系统的实验来加以确认.

3.2 人工调控拓扑超导

在自然界中,本征拓扑超导体相对比较稀少,而利用现有的体系通过人工调控实现拓扑超导则是十分有效的途径.其核心思想是: 1) 在具有拓扑性质的体系中通过人工调控实现超导;2) 在超导异质结体系中通过人工调控实现拓扑相变.下文对于这方面的研究进展进行归纳总结.

据了解，汪记严格按照国家生猪定点屠宰企业标准化建设的要求，不断完善厂区建设，增设设施设备，规范生猪屠宰操作程序，建立健全各项规章制度，配备与屠宰规模相适应的检验人员，严格落实产品检验、追溯、贮运、不可食用生猪产品无害化处理等措施。在质量管控方面，汪记配备着一套健全完备的屠宰加工管理体系。

已有研究表明可以利用包括栅极调控、掺杂以及高压等在内的多种调控手段驱动拓扑体系发生超导转变.单层WTe2是二维拓扑绝缘体[150],通过栅极调控在1 K 附近出现超导电性[151,152].最近的理论研究表明该体系的超导态是受空间反演对称性保护的高阶拓扑超导,尚有待于实验验证[153].CuxBi2Se3是通过掺杂实现拓扑超导的典型案例.在拓扑绝缘体Bi2Se3中掺入适当的金属Cu 后,该体系在3.8 K 表现出超导电性[154].随后Sasaki 等[37]在隧穿电导谱中观察到与MZM 理论相符的ZBCP信号.此外,在Bi2Se3中掺杂Sr,Nb 等也能诱导超导转变,并且研究结果表明这类体系也具有一定的拓扑性质[155-159].常压下Cd3As2是狄拉克半金属[142,160-165],8.5 GPa 时出现超导转变(Tc～2 K),并且Tc随着压强的增大而升高,在21.3 GPa 时Tc最高达到了4 K[166].同时,在针尖诱导的Cd3As2中还观察到ZBCP 信号,支持在这一体系出现拓扑超导[167].

在对畜禽养殖过程中饲料是其不可或缺的重要因素。一般情况下，在对畜禽进行管理过程中常常发现很多畜禽指标不合格的现象发生。畜禽得不到充足的饲料时在一定程度上会造成自身生长发育不健全的现象发生，很多畜禽养殖户一般都使用青饲料来作为补充畜禽的重要营养物，然而，这种饲料的转化率却非常低，长时间使用这种饲料在一定程度上对畜禽的健康生长将会带来不同程度的影响。饲料营养不充足在一定程度上对畜牧养殖也会产生不利影响。因此，相关工作人员应该以一种与时俱进的心态积极创造更多创新型、高效的管理方案，只有这样才能够保证畜牧业健康、稳定向前发展。

约瑟夫森结的微波辐射信号也可以通过集成在-样品上的基于光子辅助隧穿(photon-assisted tunneling,PAT) 的发射探测器来测量[68],如图7(d)所示.在这样的配置下,其采集结果不能像图7(b)中那样直接观察关于电压和频率的发射信号,而是基于以下公式:

4 马约拉纳零能模的输运探测

其中,e*为发射过程的有效电荷,VNW为发射结两端的电压,f0为发射信号的频率,ΔDET为探测结能隙,VDET为探测结两端的电压.如图7(e)所示,跨导关于两个结电压的峰位可由(9) 式描述,由此可以得到结发射的有效电荷e*.对于常规约瑟夫森结,其有效电荷为2e;对于拓扑约瑟夫森结,其有效电荷为1e.该实验观察到了随着平行磁场的引入,有效电荷e*从2e到1e的转变,从而验证了分数约瑟夫森效应.

4.1 零偏压电导峰

零能量是MZM 最直观的特征.它可以通过测量体系的态密度得到,在隧穿谱上对应的电导峰严格位于零能位置,在不破坏系统拓扑性质的情况下能够稳定存在,这是与平庸的安德列夫束缚态(Andreev bound states,ABSs) 的最大区别.理想状况下,当正常电子通过共振隧穿占据能隙内的态时将会产生量子化的电导.因此,量子化的ZBCP是MZM 存在的一个直接证据,并且其电导值和体系的对称性以及维度都有关系.例如在时间反演对称破缺的一维拓扑超导体中,其电导值恰好是一个量子化电导G0(2e2/h);若是在时间反演对称的拓扑超导体中,由于MZM 会形成Kramers 对,其电导值将是2G0[174];在二维、三维拓扑超导体中,对于ZBCP 的讨论还会更加复杂.实验上,由于隧穿测量的器件容易制备,所需要的实验条件容易实现,因此ZBCP 测量成为表征MZM 的首选方案.目前,实验上已经在多个体系中观察到了ZBCP 的存在,如本征的Au2Pb[114]、掺杂的CuxBi2Se3[37]、超导/半导体纳米线[38-54]、超导/拓扑绝缘体Bi2Se3[57]、超导/金属表面态Au[175]、磁性原子链[59-61]等.

早在2010 年,Yang 等[57]在利用s 波超导体和三维拓扑绝缘体构建拓扑超导时,在Sn/Bi2Se3界面处利用隧穿谱探测到显著的ZBCP,如图3(a)所示,为px+ipy超导电性的存在提供了实验支持.随后,Mourik 等[47]在NbTiN/InSb 纳米线复合结构 (图3(c))中观察到了和MZM 图像相符的ZBCP.从图3(d) 可以看出,随着平行磁场的施加出现了ZBCP,同时在旋转磁场实验中也观察到了磁场接近平行BSO时ZBCP 的消失,这与磁场驱动的拓扑相变图像吻合.同年在Al/InAs 纳米线复合结构中也报道了类似的实验结果[38].大量实验观察到的ZBCP 以及接近量子化的ZBCP[41,46]是这一领域取得的重要成果.但与此同时,理论上认为这些结果也可以通过拓扑平庸的机制解释,包括非均匀的系统参数[75]、弱反局域化[76]、耦合量子点[77,80]、Kondo 效应[78]、准马约拉纳 (空间上分离的马约拉纳束缚态,但是没有形成拓扑的MZM[81]) 以及系统的高度无序[83].材料本身质量不够高、加工过程引入界面的杂质和缺陷以及参数调控的非均匀性是引起平庸机制的重要原因,需要在后续工作中逐步优化.

图3 在超导复合结构中探测ZBCP (a) Sn/Bi2Se3 复合结构中出现的ZBCP,左、右两图分别为归一化的隧穿电导在不同温度和磁场下关于偏置电压Vbias 的关系图,Δ1,Δ2 标出了两个不同的能隙结构,在低温及低场下能观察到显著的ZBCP,引自文献[57].(b) 在超导完全覆盖的纳米线器件中观测到的MZM 迹象.左图显示了Al 完全覆盖的InAs 半导体纳米线器件的假彩色扫描电子显微镜 (scanning electron microscope,SEM) 照片,右图上方显示了隧穿电导dI/dV 关于通过纳米线的外加磁通 (水平轴) 和源漏电压 (垂直轴) 的二维图,揭示了零磁通位置的硬能隙,以及一个磁通量子Φ0 位置处的能隙内的零能态,下方显示了存在MZM情况的模拟结果,引自文献[177].(c) 第一个在超导/半导体纳米线结构中观察到ZBCP 实验中所使用器件的SEM 照片.正常金属电极Au 完全覆盖InSb 纳米线,而超导电极NbTiN 则只覆盖其中一边.下面的底门用1—4 标记,引自文献[47].(d) 图(c) 中器件在固定磁场情况下,dI/dV 与磁场转角和偏置电压V 的关系,其中A 图为当施加与纳米线平行的200 mT 磁场时,ZBCP 最大,当磁场垂直于纳米线时,ZBCP 消失,B 图为在垂直于自旋轨道耦合场BSO 的平面上施加150 mT 的旋转磁场,ZBCP 在所有角度都存在.最上方的图像显示了与A 图和 B 图中相应颜色标识处的截线,最右侧图像从上到下分别为: (i) B 垂直BSO,能隙打开,解除费米面简并,这是实现MZM 的必要条件;(ii) B 平行BSO,不同自旋能带垂直移动2EZ,在这种配置中,不会出现MZM;(iii) A 图中旋转磁场示意图;(iv) B 图中旋转磁场示意图,引自文献[47]Fig.3.Detecting ZBCP in superconducting hybrid structures.(a) ZBCP structure observed in Sn/Bi2Se3,the normalized tunnelling conductance as a function of bias voltage Vbias collected at different temperatures (left) and magnetic fields (right),with Δ1 and Δ2 indicating two different gap structures,a significant ZBCP can be observed at low temperatures and low fields,adapted from Ref.[57].(b) MZM fingerprints in full-shell nanowires.Left image shows a false-color SEM image of a full superconducting shell surrounding an InAs semiconducting nanowire.Top right shows a color map of the tunnelling conductance dI/dV as a function of external magnetic flux (horizontal axis) through the nanowire and source-drain voltage (vertical axis),revealing a hard induced superconducting gap near zero magnetic flux and a gapped region with a discrete zero-energy state around one flux quantum Φ0 .Bottom right shows the simulation results for the presence of MZM,adapted from Ref.[177].(c) SEM image of the device used in the first observation of ZBCP in superconductor/semiconductor nanowire structures.The normal metal electrode Au completely covers the InSb nanowire,while the superconducting electrode NbTiN covers only one side.The bottom gates are labelled with numbers 1 through 4,adapted from Ref.[47].(d) The relationship between dI/dV and the angle of magnetic field and bias voltage at a fixed magnetic field.Fig.A shows rotating the magnetic field |B|=200 mT in the plane of the substrate.The ZBCP is maximal when B is parallel to the nanowire and absent when B is perpendicular to the nanowire.Fig.B shows rotating the magnetic field|B|=150 mT in the plane perpendicular to BSO.Now,the ZBCP exists at all angles.The top panels show the linecuts at angles with corresponding colors in Fig.A and Fig.B.The rightmost panels show,from top to bottom: (i) The gap opening lifts the Fermi surface degeneracy when B is perpendicular to BSO,which is a necessary condition for achieving MZM;(ii) when B is parallel to BSO,different spin bands shift vertically by 2EZ,MZM is absent;(iii) schematic of the rotation of B in Fig.A;(iv) schematic of the rotation of B in Fig.B,adapted from Ref.[47].

无序导致的接近量子化的ZBCP 已经被最近的实验所证实,在相同的实验参数配置下,同时测量纳米线两端的隧穿谱,仅在一端发现了接近量子化的ZBCP,而在另一端则观察到了电导谷[84].对于MZM 和准MZM,理论研究指出其ZBCP 的峰值不会超过G0,而由无序诱导的ZBCP 有可能超过这个值.另外,对于真实的MZM,随着塞曼场的增加可能会出现马约拉纳振荡[40,176],而对于准MZM则不会出现,这些特征可以作为进一步甄别MZM的判据[85].上述实验都是基于超导半覆盖的纳米线,其优点是便于在超导覆盖的区域通过栅极调节载流子浓度或费米面;此外也有完全覆盖超导的纳米线实验[177],如图3(b) 所示,这种配置虽然通过栅极难以调节载流子浓度,但是可以有效减小其发生拓扑转变的磁场,同时降低对朗德g因子的要求,类似Little-Parks 实验[178].当通过完全覆盖纳米线的磁通为零时,实验上看到了超导邻近诱导的硬能隙 (hard gap) 结构,其中没有额外的亚能隙态 (subgap states);当引入一个磁通量子Φ0(h/(2e),h为普朗克常数,e为元电荷) 时,对应体系的缠绕数为±2π,这时在能隙内观察到稳定的ZBCP,与理论结果吻合较好.最近的实验观测到类似的实验结果,但给出了平庸的解释,他们认为实验中观测到的ZBCP 结构由隧穿结的长短决定,而与纳米线无关[86].相对于短结,在长结中总会形成量子点,当零磁场下的ABSs 能量和超导能隙接近时,在量子点基态从YSR 态向双重态 (doublet state) 发生转变的量子相变点附近,可以同时观察到零号瓣(lobe) 中的硬能隙结构和贯穿整个一号瓣的ZBCP,这个现象会被误认为是MZM.因此,需要更加完备的实验来探究ZBCP 的真正起源.

4.2 库仑阻塞谱

上文介绍的隧穿谱探测只能提供MZM 的局域信息,而利用库仑阻塞谱可以给出系统的非局域信息,作为验证MZM 的补充,下文将介绍这方面的研究进展.

图4(a) 展示了利用库仑阻塞谱探测MZM 的原理.不同颜色的曲线代表不同的输运过程.这些过程由EN(NG)=EC(NG-N)2+pNE0决定,式中EN为超导岛能量,EC为充电能,NG为栅极引起的电荷变化,N为电子占据数,pN有两个取值,pN=1 对应奇宇称,pN=0 对应偶宇称,E0为最低准粒子态能量.对于正常金属形成的岛,当调节其栅极电压时,电子将会逐个地进出岛;对于超导邻近的纳米线构成的超导岛,当体系处于拓扑平庸的状态时,若E0＞EC,电子将成对地进出超导岛(橙色曲线);若E0＜EC则以单电子的形式进出超导岛 (绿色曲线),但是随栅极电压调控会表现出两个不同的周期,对应于进出岛中的电子数目的奇偶宇称变化,这个结果反映了进入岛中的奇数电子是未配对的,并且要求额外的能量E0来实现偶数电子的配对.不过,对于拓扑体系,不需要这个额外能量,因为此时奇数电子可以占据零能量的马约拉纳态.这在实验上导致的结果是: 当调节栅极电压时,可以看到完全等周期的单电子过程 (红色曲线),前面提到的奇偶变化将会消失[179,180].该现象在实验上已经由Albrecht 等[181]观测到,他们发现随着平行磁场的增加,对应2e 电子输运的库仑峰发生劈裂,产生1e 电子输运,从So,e(奇数和偶数电子的库仑峰间距) 的图像上也确认了Se=So的结果,这与理论预期相符.并且,不同长度的超导岛器件的库仑阻塞谱和电子隧穿谱同时显示了由马约拉纳耦合带来的马约拉纳振荡及其振幅关于岛长的指数依赖行为,进一步验证了MZM 的存在.此后的实验重复了这一结果[180],从图4(b) 中的二维图可以直观地观察到,随着B//的增大,2e 周期库仑峰向1e 周期库仑峰转变的过程,下方的So,e图像显示了相应的振荡行为.此外,该实验还发现了2e 电子输运情况下岛内的奇宇称行为,图4(c) 清楚地显示了2e 周期偶宇称向2e 周期奇宇称转变的过程.他们把这种过程归结于岛中出现了负能量的基态,如图4(a) 中的青色和紫色曲线所示,当岛的基态能量为-EC(紫色曲线) 时,电子输运过程恰好重新变为2e,但是输运却发生在奇宇称的抛物线之间,这一发现进一步完善了超导岛器件的物理图像.Vaitiekėnas 等[177]在超导完全覆盖的半导体纳米线中也观察到了类似的结果,他们在单根纳米线上制作了多个不同长度的岛 (图4(d)),观察到从零号瓣到一号瓣发生2e 向1e 转变的过程,并且观察到了So,e振荡振幅与岛长度之间的指数依赖关系,结合之前发现的ZBCP (图3(b)),他们认为该体系中存在MZM.而在近期同样利用超导完全覆盖的纳米线实验中[88],虽然也观察到了类似的等周期的单电子过程,但是在相应的隧穿实验中,无论是在左端还是在右端都没有观察到ZBCP.因此,这里观察到的单电子过程被解释为拓扑平庸的机制,即体系的能隙内存在准连续态,它使得整个体系更容易发生单电子过程,数值模拟结果也支持这种解释.

图4 利用库仑阻塞谱探测MZM (a) 利用库仑阻塞谱探测MZM 的原理;(b) 上图是电导dI/dVb 关于磁场 B// 和栅极电压VPG的关系,展示了2e 周期向1e 周期转变的过程;下图展示了库仑峰间距So,e 随磁场 B// 的振荡,引自文献[180];(c) 类似 (b)图,展示了随磁场出现的2e 电子输运过程的宇称从偶宇称到奇宇称的转变,插图为转变区的放大图,引自文献[180];(d) 左上图为利用超导全覆盖纳米线制作的包含6 个具备独立栅极的超导岛器件的SEM 照片;左下图展示了电导dI/dV 关于磁场 B// 和栅极电压VG的二维图,右图为库仑峰振荡振幅A 关于岛长度L 的关系曲线,满足指数关系 A=A0e-L/ξ,引自文献[177]Fig.4.Using Coulomb blockade spectroscopy to detect MZM: (a) Principal of detecting MZM by Coulomb blockade spectroscopy.(b) Top panel shows the relationship between the conductance dI/dVb and the magnetic field B// and gate voltage VPG,displaying a transition from 2e-periodic Coulomb-peak to 1e-periodic Coulomb-peak.Bottom panel shows the Coulomb peak spacing So,e as a function of magnetic field B//,exhibiting clear oscillations,adapted from Ref.[180].(c) Similar to (b),the parity undergoes a transition from even to odd in the 2e-periodic electron transport process as the magnetic field increases.The inset shows a zoom view of the transition region,adapted from Ref.[180].(d) Top left panel shows the SEM image of six superconducting islands with individual gates constructed on a single full-shell nanowire.Bottom left panel shows the conductance dI/dV as a function of magnetic field B‖ and gate voltage VG.Right panel shows the relationship between the oscillatory amplitude A and the island length L,which satisfies an exponential relationship A=A0e-L/ξ,adapted from Ref.[177].

4.3 非局域电导

除了上述基于库仑阻塞谱的非局域测量外,理论还提出基于三端器件的非局域电导测量.通常的两端测量只能探测最接近正常电极处的态,无法给出超导邻近区域的全局性质,这种测量方式很难区分由平庸机制导致的低能态和真实的MZM.

其中Δ0为超导能隙,D为透射系数,φ为相位差.可以看到在透射率不为1 时,s(p) 波超导体的能量相位关系是2π(4π) 周期的,对应的电流相位关系(current phase relationship,CPR)也同样是2π(4π) 周期的,图6(a),(b)分别给出了两种情况下的能量和电流关于相位的关系.理论上,借助这一点可以在基于拓扑超导的实验中观察到4π 周期的超导衍射 (干涉) 图样,这一效应也被称作分数约瑟夫森效应.但实际上,我们很难从实验上直接观察到这种现象.因为准粒子中毒[190,191]会使体系的费米子宇称发生变化,体系的能量将会沿着两支能谱能量最低的部分演化,其结果是体系的能量相位关系重新回到2π 周期.因此,很难采用直流约瑟夫森效应区分它和常规超导结.为了能够从实验上观察到分数约瑟夫森效应,我们需要在MZM 弛豫时间内进行测量.实验上可以借助交流约瑟夫森效应观察约瑟夫森结的微波发射,得到在半个约瑟夫森频率fJ/2=eV/h处的发射信号;或者利用逆交流约瑟夫森效应观察奇数Shapiro台阶消失的现象,目前已经在多个体系中观测到这些现象[62-71].

图5 非局域电导探测 (a) 用于测量电导矩阵的三端器件配置,两端正常电极连接到中央接地的超导区域,其中的电势可以通过栅极控制,引自文献[186];(b) 在 L≫ξ 下,能量空间中可能的散射过程示意图,引自文献[182];(c) 电导矩阵关于磁场B 和偏置电压VL,R 的二维图,引自文献[183];(d) 电导矩阵关于磁场B 和偏置电压VT,B 的二维图,引自文献[184]Fig.5.Non-local conductance spectroscopy measurement: (a) Three-terminal device configuration.Two normal electrodes are connected to central grounded superconducting region,where the potential can be controlled by the gates,adapted from Ref.[186].(b) Illustrations of possible scattering processes in energy space when L ≫ξ,adapted from Ref.[182].(c) The conductance matrix as a function of magnetic field B and bias voltage VL,R,Adapted from Ref.[183].(d) Two-dimensional plot of the conductance matrix as a function of magnetic field B and bias voltage VT,B,adapted from Ref.[184].

其中的GLL,GRR分别对应两端的局域电导,而GRL,GLR则对应非局域电导.在L≥ξ(L为超导区长度,ξ为诱导相干长度) 的条件下,不同能量区间系统出现如图5(b) 所示的输运过程:|E|＜Δind(E为准粒子能量,Δind为诱导能隙),准粒子将被直接反射回去,对非局域电导无贡献;Δind＜|E|＜Δ(Δ为电极超导能隙),准粒子被传输到另一端,变为电子 (正常传输) 或空穴 (交叉安德列夫反射),贡献非局域电导;|E|＞Δ,超导电极吸收准粒子(传导到地).基于这一输运过程,文献[182]指出非局域电导谱可以用于探测系统的全局性质: 电极超导能隙、诱导超导能隙和诱导相干长度.这使得利用非局域电导谱探测能隙从关闭到打开的拓扑相变过程成为可能.并且,他们的研究进一步指出,在拓扑相变点,非局域电导与能量呈准线性关系,对应于I ∝V2(V为偏置电压),作者将这样的系统称为安德列夫整流器 (Andreev rectifier).

图5(c) 展示了基于InAs 纳米线三端器件测量得到的电导矩阵[183],在局域电导谱中,左右两端均观察到了稳定的ZBCP,并且在非局域电导谱中观察到了在ZBCP 出现前的能隙关闭,以及在能隙关闭处关于偏置电压的奇函数行为,与安德列夫整流器的物理图像吻合.但是,此处未观察到关闭的能隙重新打开,可能与系统的无序性有关.后续在InAs 量子阱的实验中 (图5(d)),两端局域电导谱同时观察到了稳定的ZBCP、能隙关闭再重新打开的现象,与理论预期十分符合[184].另外,对于强无序和小尺寸系统,理论提出了通过探测冯诺依曼熵的方式来弥补非局域电导探测的缺陷[185].

除上述原理外,非局域电导还可以用来探测局域BCS 电荷,基于如下公式:

◆以“出镜率极高”而著称的科普明星——其无所不知、什么主题都能讲的背后，不过是天性聪明加上临阵磨枪翻了几本书.

其中,α=R,L,E0为ABS 能量,sym (asym) 标记电导的对称(反对称)分量≡[Gαβ(V)±Gαβ(-V)]/2.这个公式给出的是局域的BCS 电荷,而dE0/dμ(μ为纳米线的化学势) 则反映整体的BCS 电荷.因此,当两者差异较大时,表明该ABS 在纳米线中心的比重更大,与MZM局域在两端的行为不符,这可以用于区分马约拉纳束缚态和平庸的ABS[186].另外,由于MZM 是中性的,在马约拉纳振荡关于磁场的转折点处,应该没有非局域的电导.实验上已经利用这一结论来分辨低能ABS 的拓扑性质[187].

由表3可知，产城融合发展水平（ici）、市场化程度（mar）和农业发展水平（agr）存在单位根，科技进步（tec）、金融支持水平（fin）和人力资本（edu）则拒绝了“存在单位根”的原假设，而各个变量的一阶差分都拒绝了“存在单位根”或接受“平稳序列”的原假设，即残差项无单位根。

4.4 分数约瑟夫森效应

4.4.2 逆交流约瑟夫森效应

(2)图书借阅类数据。阅读可以在课堂外拓宽大学专业的深度、增加学生知识面的广度，有助于学生多方面拓展思维，掌握分析问题和思考问题的新视角和新思维，也是创新能力培养不可或缺的。图书借阅类数据来源于学校图书馆的数据中心，包括学生借阅书籍报刊的类别、借阅频率、借阅书籍阅读的时间以及学生多次借阅的书籍等。

容易验证这里的γ1,γ2算符都是自共轭的,它们具有和马约拉纳费米子相同的物理.超导体中Bogoliubov 准粒子可以视为电子和空穴的叠加,根据粒子空穴对称性的要求,能量E处的准粒子产生和湮灭算符应满足γ(E)=γ†(-E),这意味着在费米能处这个关系将变为γ(0)=γ†(0),从而满足马约拉纳费米子的自共轭关系.因此,这个零能量的激发模式被称作马约拉纳零能模.为了实现可观测的MZM,要求两个MZM 在空间上分离,否则它们将重新耦合成单粒子态;另外常规的s 波超导体中的电子采用自旋单态配对,这使得它们的叠加不能满足自共轭条件.为此,需要引入一种等自旋的电子配对机制,其空间波函数最简单的形式为p 波,相应的体系称为p 波超导[5].除此之外,还有一些具有不同对称性的拓扑超导体系[7](见表1),其承载的MZM 也存在差别.譬如一维p 波超导体的两端分别存在一个MZM,具有时间反演对称的DIII 类拓扑超导存在MZM 的Krammers 对,而具有手性对称的一维BDI 类拓扑超导体两端可以存在多对MZMs[99].值得指出的是,局域存在多个MZMs 会增加对其进行编织的难度[100].

图5(a) 展示了利用三端器件探测非局域电导的配置,测量基于如下电导矩阵:

图6 约瑟夫森结的能量 (电流) 和相位的关系以及Landau-Zener 跃迁机制示意图 (a) 常规约瑟夫森结的能量相位关系 (上方)和电流相位关系 (下方) 示意图,呈现出2π 周期性,透射率分别为D=1 (橙色曲线) 和D=0.6 (蓝色曲线);(b) 拓扑约瑟夫森结的能量相位关系 (上方) 和电流相位关系 (下方) 示意图,呈现出4π 周期性,透射率分别为D=1 (橙色曲线) 和D=0.6 (蓝色曲线);在发生零次 (绿色实线) 和两次 (蓝色虚线) LZT 后,能量 (c) 和电流 (d) 关于相位φ 的关系,(c) 中灰色和红色区域分别对应于绝热和非绝热演化过程,绿色实线与蓝色虚线分别代表绝热极限 (呈2π 周期性) 和非绝热极限 (呈4π 周期性),引自文献[74]Fig.6.Energy (current) vs.phase relationship and LZT in Josephson junctions: (a) The energies and the currents in the conventional Josephson junction as functions of the phase difference φ for D=1 (orange) and D=0.6 (blue);(b) the energies and the currents in the topological Josephson junction as functions of the phase difference φ for D=1 (orange) and D=0.6 (blue);energy (c)and current (d) vs.phase φ after zero (green solid line) and two (blue dashed line) LZTs occurred,in (c),the gray and red regions correspond to adiabatic and non-adiabatic evolutions,respectively,the green solid line (2π periodicity) and blue dashed line (4π periodicity) represent the evolution in the adiabatic and the non-adiabatic limits,adapted from Ref.[74].

4.4.1 交流约瑟夫森效应

交流约瑟夫森效应,即向约瑟夫森结施加一个电压V时,在结区中将会出现高频 (fJ/2=eV/h)交变电流,并向外辐射信号.图7(a) 是在HgTe 二维拓扑绝缘体上用Al 制作的约瑟夫森结[65].为了测量约瑟夫森结产生的微波辐射,实验上将结上的直流信号和交流信号通过偏置器解耦,然后分别进入直流和交流测量线路,其中交流信号通过微波放大器后进入频谱分析仪得到结的辐射信号.图7(b)中的灰色直线标注了不同频率的发射信号,其中fJ,2fJ为常规约瑟夫森结的发射信号,而fJ/2 的信号即为拓扑约瑟夫森结的发射信号,高频处的振荡可能来自于电磁环境的影响.可以看出,拓扑结信号明显强于常规结信号,并表现出显著的展宽.常规约瑟夫森结的展宽可能来自于配对电流或者准粒子电流的波动以及环境噪声的影响;而在拓扑结中,它还和宇称弛豫以及电离到连续谱的弛豫过程有关,更大的线宽意味着更短的相干时间.除了存在使体系从4π 向2π 转变的机制外,还有使体系从2π 向4π 转变的Landau-Zener 跃迁机制 (Landau-Zener transition,LZT)[74],如图6(c),(d)所示.它可以使不同宇称的两支能谱在交叉点附近发生跃迁,从而产生4π 周期的能量演化.在单库珀对晶体管中,很早就观测到了LZT 现象[73].在图7(b)实验中,LZT 发生的激励电压存在上限 (VLZ≪6 μV),但由于实际的实验激励已经远超这个极限,因此可以排除LZT 过程导致的平庸4π 信号.

生物源于生活，服务于生活.在当前教学中，由于受传统教学模式的影响，生物教学课时安排较为紧张，生物教师很少组织学生参加野外活动、参观生产基地等生物知识类的教学活动.由于高中生物教学缺少色彩，学生只能被动、机械地学习生物，自主性学习兴趣不高涨，难以有效地将生物知识与生活相联系，生物思维得不到有效激发.

图7 交流约瑟夫森效应的探测 (a) HgTe 约瑟夫森结器件的假彩色SEM 照片,蓝色为被绝缘层覆盖的HgTe,紫色为Al 电极,黄色为栅极.并联电阻RS 使结电压保持稳定.通过测量跨越结和RI 的电压,可以直接得到V 和I.射频信号通过偏置器进入到放大电路中,最后进入频谱分析仪.引自文献[65].(b) 拓扑约瑟夫森结辐射功率关于直流电压V 和探测频率fd 的二维图,依次可以看到 fJ/2 ,fJ 和 2fJ 的发射线,引自文献[65].(c) 欠阻尼约瑟夫森结的发射线,引自文献[192].(d) 利用片上探测器探测约瑟夫森结的辐射信号,从左到右依次为: (i) 放置在3 个栅极上的纳米线约瑟夫森结的SEM 照片,插图展示了结的假彩色SEM 照片,其中外延Al 壳以青色突出显示;(ii) 纳米线约瑟夫森结 (蓝色框) 和检测结 (红色框) 之间耦合电路的光学照片;(iii) 两个并联的约瑟夫森结构成的微波探测器的SEM 照片,引自文献[68].(e) 探测器的跨导dIPAT/dVNM 关于探测器电压VDET 和纳米线电压VNW的二维图,图中标出了理论预言的2e (绿色虚线) 和1e (红色虚线) 电子行为的峰位,在磁场B=650 mT 处观察到了1e 电子发射行为 (橙色实线),引自文献[68]Fig.7.Detection of AC Josephson effect.(a) False-color SEM image of HgTe Josephson junction device.Blue represents HgTe covered by an insulating layer,purple represents Al electrodes,and yellow represents the gate.The shunt resistor RS enables stable voltage bias.The measurement of the voltage across the junction and RI is directly yields V and I.The rf signal enters the amplification circuit through the bias T circuit and finally enters the spectrum analyzer,adapted from Ref.[65].(b) The power collected from the topological Josephson junction as a function of the DC voltage V and the detection frequency fd.The emission lines of fJ/2,fJ and 2fJ can be seen in order,adapted from Ref.[65].(c) Emission lines of an underdamped Josephson junction,adapted from Ref.[192].(d) Detection of the Josephson junction radiation signal using an on-chip detector.From left to right: (i) SEM images of nanowire Josephson junctions placed on three gates.The inset shows a false-color SEM image of the junction,with the epitaxial Al shell highlighted in cyan.(ii) Optical image of the coupling circuit between the nanowire Josephson junction (blue box) and the detection junction (red box).(iii) SEM image of the microwave detector composed of two parallel Josephson junctions,adapted from Ref.[68].(e) Transconductance dIPAT/dVNM as a function of the detector voltage VDET and the nanowire voltage VNW.The dashed lines indicate the theoretically predicted peak positions of the 2e (green) and 1e (red) electron behavior.1e electron emission behavior (orange solid line) is observed at a magnetic field of B=650 mT,adapted from Ref.[68].

利用超导邻近效应在传统s 波超导体和其他材料形成的异质结中诱导出拓扑超导是目前研究拓扑超导的主流方案.其最早由Fu 和 Kane[15]提出,他们研究了在三维拓扑绝缘体表面的超导邻近效应,指出在这个体系的界面处将会形成类似px+ipy波超导,当打破时间反演对称性,将在体系的涡旋处出现MZM.在此基础上,他们提出了在s 波超导体/量子自旋霍尔绝缘体中出现时间反演对称的MZM 方案[17].类似的方案,也被其他研究者用于反常量子霍尔绝缘体[168]与拓扑半金属[169-171].当前寻找MZM 的研究主要集中于s 波超导体/强自旋轨道耦合半导体的复合体系.这一方案需要提供适当的塞曼能使系统发生拓扑相变,它可以通过磁性绝缘体[19]、少层半金属[24,25]或者施加垂直SOC的磁场[21,22]来实现.这个方案的理想载体是具有强SOC 的半导体纳米线或者二维电子气.其中,基于s 波超导体/强SOC 半导体纳米线复合结构的研究方案进展最为引人注目.此外,人们也提出利用具有更强SOC 的金属表面态来实现拓扑超导[27].在超导衬底上放置磁性原子链模拟一维Kitaev 链模型是实现拓扑超导的另一途径,旨在利用Yu-Shiba-Rusinov (YSR) 态杂化出现p 波配对[172,173].

为探测并甄别来自MZM 的信号,实验上需要利用MZM 自共轭、非局域、零能量以及非阿贝尔统计的特性来产生观测指标.首先,利用MZM 是拓扑超导边界的零能激发这一特点,通过隧穿实验可观测到ZBCP;由于MZM 在拓扑超导体中对应着单电子的过程而不是库珀对,因此可以从库仑阻塞谱中观察到对应的现象;MZM 在空间上非局域的关联特性在非局域电测量上也有所体现;不仅如此,由于拓扑超导不同于通常s 波超导的配对性质,基于分数约瑟夫森效应通过 (逆) 交流分数约瑟夫森效应与电流相位关系的测量 (current-phase relationship,CPR) 也可以找到MZM 存在的证据.

此外,根据理论计算,在欠阻尼的约瑟夫森结中,当MZMs 间的耦合强度适中时,除了常规发射线fJ(黄色虚线) 外,还会在发射线fJ/2 处 (黑色虚线) 出现两条按照贝塞尔函数振荡的发射线 (蓝色-和橙色)[192],如图7(c) 所示,这可以作为验证MZM的又一探测手段.

③如果采运本人的诊断方法,可以最大限度的避免医疗资源的浪费。本诊断中有“如果患者“四部27点规律”查体后,不符合“两部2点规律或两部2点规律以上”,则不需要拍X光、CT、MRI。这样先行压痛点检查既可避免漏诊,又可免除拍X光、CT、MRI的检查,从而最大限度的避免医疗资源的浪费,

在治疗前和治疗第2、4、8、12周末采用HAMD评判患者抑郁程度，共24项目，每项按实际情况进行打分，总分＜8分为正常无抑郁症状；8～20分为可能存在抑郁症状；21～35分为存在抑郁症状；＞35分为严重抑郁。临床疗效评分：治愈，治疗结束后抑郁评分降低超过75%；显效，治疗结束后抑郁评分降低超过50%～74%；有效，治疗结束后抑郁评分降低25%～49%；无效：治疗结束后抑郁评分降低＜25%或无改变。总显效率=治愈率+显效率。

当两个拓扑超导体耦合在一起构成约瑟夫森结时,它们的安德列夫表面态将会杂化并在结区中形成ABSs,这些束缚态将会对约瑟夫森电流产生重要影响.因此,可以借助观测特殊的约瑟夫森信号甄别拓扑超导和常规超导[188].

逆交流约瑟夫森效应,即向约瑟夫森结施加一个微波信号时,在I-V曲线上将会出现一系列台阶形 (Shapiro 台阶) 的直流分量[193].在InAs 纳米线中,已经观测到逆交流分数约瑟夫森效应[62].在3 GHz 下,第1 级Shapiro 台阶随着垂直BSO方向磁场的增加而逐渐消失,这和分数交流约瑟夫森效应所预测的奇数台阶消失、偶数台阶保留的图像吻合.后续实验也报道了该现象,图8(a) 展示了在三维拓扑绝缘体HgTe 中测量到的逆交流分数约瑟夫森效应结果[63].目前,多数实验只观察到第1 级台阶消失,个别实验观测到了第3 级乃至第9 级台阶的消失[64,194].仅通过第1 级台阶消失的现象还不能完全归因于分数约瑟夫森效应,它有可能来源于热效应[79]和LZT.对此,可以通过观测磁场驱动的拓扑转变[62,71]或多级奇数台阶的消失 (偶数台阶保留) 来排除[64,194].需要注意的是,在利用逆交流约瑟夫森效应研究拓扑超导时,微波频率对拓扑效应的观察具有重要影响[74,195].在I2π≫I4π(I2π,I4π分别为2π,4π 超流大小) 的条件下,当驱动的微波频率f＜f4π=2eRnI4π/h(Rn为正常态电阻)时,结的动力学特性φ(t) 相对更慢且非线性,对应的电压变化V(t)是非谐函数,这使得它对4π 分量的响应会更加显著,实验上更容易观察到分数约瑟夫森效应;而当f＞f4π时,V(t)变得接近正弦函数,以至于更倾向于响应2π 分量的信号,实验上仅能观察到常规约瑟夫森效应.因此,需要选择合适的微波频率观测体系的拓扑效应.

图8 探测逆交流约瑟夫森效应 (a) 在三维拓扑绝缘体HgTe 中观察到的分数约瑟夫森效应.左图为微波功率f=2.7 GHz 时,电压分布 (数据点按电压分组) 关于微波电流Irf 和偏置电压V 的二维图,右边的直方图清晰地显示第1 级台阶受到显著抑制,引自文献[63].(b) 在频率frf=0.953 GHz 时的微分电阻dV/dI 关于功率Prf 和电流I 的二维图,引自文献[67].20 mT 时在平行磁场 (c) 和垂直磁场 (d) 下观测到的电压分布关于微波功率P 和偏置电压I 的二维图,40 mT 时在平行磁场 (e) 和垂直磁场 (f) 下观测到的电压分布关于微波功率P 和偏置电压V 的二维图,引自文献[71]Fig.8.Detection of the inverse AC Josephson effect.(a) Fractional AC Josephson effect observed in a three-dimensional topological insulator HgTe.Left panel shows a 2D plot of voltage distribution (data points grouped by voltage) as a function of microwave current Irf and bias voltage V at a fixed frequency f=2.7 GHz,with the first step significantly suppressed.Right panel is a histogram showing the same result,adapted from Ref.[63].(b) Differential resistance dV/dI as a function of power Prf and current I at a frequency of frf=0.953 GHz,adapted from Ref.[67].Voltage distribution as a function of microwave power P and bias voltage V under parallel (c) and perpendicular (d) magnetic fields of 20 mT.Voltage distribution as a function of microwave power P and bias voltage V under parallel (e) and perpendicular (f) magnetic fields of 40 mT,adapted from Ref.[71].

除了观察上述Shapiro 台阶加倍现象外,在微波响应的二维图中零号台阶第一节点的打开也是4π 超流的证据之一[67],如图8(b) 所示.从电阻分路结模型 (resistively shunted junction,RSJ) 模拟的结果来看,这种节点打开的现象在理想状况下也可以出现在其他位置,但在考虑到热效应后,只出现在零号台阶的位置.利用这个现象可以在高达16f4π的微波频率下探测4π 超流成分,大大拓展了研究范围、降低了观测难度.

此外,Dartiailh 等[87]在InAs 量子阱中观察到了平庸的第一级台阶消失的现象,并将其归结于LZT 过程,这里LZT 在能谱交叉点处的概率可以表示为[72]

首先将本文方法所需数据量与文献[5]中基于矩阵分析的方法、文献[10]中基于GFFT的方法和文献[11]中基于Gröbner基改进的GFFT方法进行对比，m取值为3～8，仍然选取与图4中相同的6种RS码进行研究，且每种RS码对应误比特率分别为0.02、0.01、0.005、0.002、0.001和0.0004.本文方法在各种条件下所需数据量可由式(32)获得；对于文献[5]中方法，其分析矩阵必须满足行数大于列数，因此所需数据量至少为m2n2；基于GFFT的方法至少需要50组完整码字，相应的数据量为50mn.最终，得到对比结果如表4所示.可以看出，相同条件下本文方法所需数据量更小.

显然PLZT强烈依赖于系统的透射率D,直接导致在高透射率的器件中容易观察到这一现象.有鉴于此,Fischer 等[71]通过施加不同方向的磁场对拓扑和平庸的过程加以区分,并通过扩展的电阻电容分路结模型(resistively and capacitively shunted junction,RCSJ) 对拓扑相变进行界定.图8(c),(d)分别展示了在20 mT 平行和垂直磁场测量到的结果,其中都观察到了显著的第1 级台阶消失现象,但是理论指出垂直磁场的施加不能带来拓扑相变[26].因此,他们将这里的结果归因于平庸的LZT过程.进而在更高磁场下(图8(e),(f)),在平行磁场条件下仍然观察到第1 级台阶消失的特征,而在垂直磁场时则出现所有台阶.据此,他们指出通过平行磁场施加的磁通在 0.25＜Φ/Φ0＜0.5 时,结中的4π 超流起源于拓扑性质.

4.4.3 电流相位关系

除了上述提到的 (逆) 交流约瑟夫森效应外,直接测量CPR 也可以作为一种探测MZM 的手段.虽然在有限温度时,CPR 在平衡态下没有4π周期性,但在较低的温度下,它明显偏离正弦函数,并且从(9)式和(10)式来看,这种偏离原则上与透射率没有太大的关系,这可以用来区分常规和拓扑的CPR[188].另外,在超导与拓扑材料的复合体系中,非正弦的CPR 还反映了高透射率的边界态贡献,边界态的超导邻近是实现拓扑超导的关键[196].因此,CPR 的测量可以作为一种辅助探测MZM的手段.图9(a) 展示了在二维拓扑绝缘体HgTe中观察到的非正弦的CPR[197],同时在这个体系中还观察到了奇数Shapiro 台阶的消失[63],印证了该体系中4π 超流的拓扑起源.

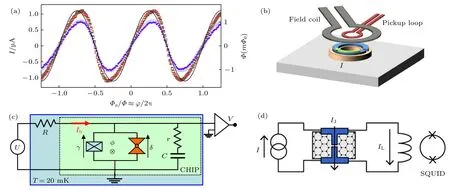
图9 电流相位关系的测量 (a) 在Nb/3D-HgTe/Nb 中测量到的CPR,相比完全对称的正弦形式 (黑色实线) 有一定的倾斜,引自文献[197].(b) 利用扫描SQUID 显微镜测量CPR 的原理图.分别显示了励磁线圈 (field coil)、拾取回路 (pickup loop)和感生电流I,引自文献[197].(c) 利用极不对称SQUID 测量CPR 的原理图.其中γ 表示参考结的相位,δ 表示待测结的相位,Ib 为激励电流,引自文献[201].(d) 利用单结耦合SQUID 测量CPR 的原理图.电流I 在结中激励起超流,并在环中产生磁通.产生的磁通通过磁通变换器耦合到SQUID,引自文献[203]Fig.9.Measurements of current-phase relationships.(a) Measured CPR in Nb/3D-HgTe/Nb,exhibiting a slight forward skewness compared to the perfectly symmetric sinusoidal form (black solid line).Adapted from Ref.[197].(b) Schematic of measuring CPR using a scanning SQUID microscope.The field coil,pickup loop,and induced current I are shown.Adapted from Ref.[197].(c) Schematic of measuring CPR using a highly asymmetric SQUID.Here,γ represents the phase of the reference junction,δ represents the phase of the measured junction,and Ib is the excitation current,adapted from Ref.[201].(d) Schematic of measuring CPR using a single junction coupled to a SQUID.The current I excites a supercurrent in the junction and generates magnetic flux in the loop.The generated flux is coupled to the SQUID through a flux transformer.Adapted from Ref.[203].

尽管测量CPR 有多种方式,但其核心都是确定超流变化过程中的对应相位,具体方法如下.i) 利用扫描超导量子干涉器 (superconducting quantum interference device,SQUID) 显微镜测量.其工作原理如图9(b) 所示,通过施加磁场在单结SQUID 样品中激励超流的同时,测量其互感电流反馈的磁场,通过激励电流和反馈电流之间的关系得到样品的CPR[197,198].ii) 将样品和一个超流远大于它的结并联组成一个极不对称的SQUID[199-201],如图9(c)所示,此时两个结相位和磁通的关系为φ2-φ1=2πΦ/Φ0(φ1,φ2分别为两个结的相位差,Φ为外加磁通),而对应的总的CPR 为Is(Φ)=Is1(φ1)+Is2(φ2)(Is1,Is2分别为两个结的超流).当Ic1≫Ic2(Ic1,Ic2分别为两个结的临界超流) 时,可以近似认为φ1≈φc1(结1 临界超流的对应相位),此时CPR 变为Is(Φ)≈Ic1+Is2(2πΦ/Φ0+φc1) .因此,只要从实验上得到该SQUID 的临界超流与磁通的关系,便能够得到第2 个结的CPR.实验上,这样的SQUID 可以通过栅极电压对两个结区分别调节或者让待测结并联一个超流远大于它的参考结来实现.iii) 利用互感电路将单结SQUID 耦合到一个SQUID 磁力计来测量通过单结SQUID 的磁通,通过公式Φ=2πVSQUID/VΦL(VSQUID为磁力计的电压,VΦ为磁通变换器的转移函数,L为单结SQUID 电感)得到单结的相位差[202,203],如图9(d)所示,从而得到其CPR.

4.4.4 能量相位关系

除了测量CPR 外,直接测量能量和相位之间的关系也可以用于探测MZM.从常规超导与非常规超导构成的约瑟夫森结的能量相位关系(9)式和 (10) 式可知,对于偏离弹道极限 (D→1) 的情况,在π 相位时,拓扑超导的能隙是完全关闭的,而常规超导则是打开的.因为ABSs 的存在会在点接触谱上反映出来,因此利用正常电极可以探测结区能隙的变化.图10(d) 所示的实验利用点接触谱,在排除了由于电极的尺寸效应所带来的信号改变后,得到了和理论模拟结果相符的能隙关闭的点接触谱信号.图10(e) 展示了在结区中心处,通过半个磁通时,观察到的微能隙几乎完全关闭的点接触电阻行为.这些结果证实了Pb/Bi2Te3复合结构中受拓扑保护的超导能隙的存在[204].在另一个基于Bi2Te3拓扑绝缘体实现Fu-Kane 约瑟夫森三结模型的实验 (图10(a)) 中,用同样的方法再次验证了这个结果.除了观察到微能隙的关闭,该工作还验证了10 多年前Fu-Kane 模型所预言的约瑟夫森三结的相图[205],如图10(b) 所示.这为后续基于该模型进行编织乃至基于表面编码方式[206]实现通用拓扑量子计算奠定了基础.

图10 能量相位关系的探测 (a) Bi2Te3 约瑟夫森三结的假彩色SEM 照片.在Bi2Te3 薄片表面制作了一个由两个超导回路 (蓝色)连接的约瑟夫森三结.使用两个半匝线圈在回路中施加局部磁通.Au 电极用于检测三结的中心和末端处的ABSs,引自文献[205].(b) 在T=0.25 K 处测量得到的dV/dIb 关于电流IR 和IL (施加磁通) 的二维图,测量结果大体上和理论预测的约瑟夫森三结相图吻合,引自文献[205].(c) 利用隧穿结测量能量相位关系的原理图.超导环 (蓝色) 构成SQUID,激励电流IIN 用作超流干涉 (衍射) 测量,电压VT 用作隧穿测量,引自文献[208].(d) Bi2Te3 约瑟夫森结的假彩色SEM 照片.Pb 作为超导电极,Pd 电极用来探测点接触谱,A、B 和C 分别代表结的两端和中心,引自文献[204].(e) 红色和黑色曲线为接近π 相位时的接触电阻随电流Ib 的变化,蓝线为正常态电阻,可以观察到～95%的峰高变化,反映了能隙的关闭.引自文献[204].(f) 态密度 (density of states,DOSs) 关于能量E 和磁场 ΔB⊥ 的二维图,图像显示了几条离散的ABSs,引自文献[208]Fig.10.Detection of energy-phase relationships: (a) False-color SEM image of a Josephson trijunction fabricated on the surface of Bi2Te3 with two superconducting loops (in blue).Local magnetic flux is applied to the loops using two half-turn coils.Au electrodes are used to detect the ABSs at the center and ends of the junction.Adapted from Ref.[205].(b) The dV/dIb as a function of the currents IR and IL (for applying magnetic flux) measured at T=0.25 K,in good agreement with the theoretically predicted Josephson trijunction phase diagram.Adapted from Ref.[205].(c) Schematic of measuring energy-phase relationships using a tunnel junction.The superconducting loop (blue) forms a SQUID,and the excitation current IIN is applied to observe supercurrent interference(diffraction),while the voltage VT is applied for tunneling spectroscopy.Adapted from Ref.[208].(d) False-color SEM image of a Josephson junction in Bi2Te3.Pb is used as the superconducting electrode,and Pd electrodes are used to detect point-contact spectra at points of A,B and C,which correspond to the ends and center of the junction,adapted from Ref.[204].(e) Contact resistance as a function of current Ib near the π phase.The blue line represents the normal state resistance.The peak height change ratio of～95% from 147 Ω (red) to 8 Ω (black) reflects the closing of the energy gap,adapted from Ref.[204].(f) Density of states (DOSs)as a function of energy E and perpendicular magnetic field ΔB⊥,showing several discrete ABSs,adapted from Ref.[208].

实际上,利用隧穿谱测量,也可以直接给出约瑟夫森结中ABSs 能谱关于相位的关系[207].图10(c)展示了利用隧穿探测能量相位关系的原理图[208],这里超导电极构成了一大一小结组成的SQUID,并在第一个结 (JJ1) 处增加了超导的探测电极.这种结构的优点在于,它可以同时进行多种测量: 利用隧穿探测电极可以进行隧穿探测,利用SQUID可以进行超导量子干涉实验,还可以利用栅极对结区调控,将其中一个约瑟夫森结隔离开,实现对另外一个结的单独测量.这种测量方式可以尽可能多地获取样品的信息,为MZM 的存在提供更加准确的实验证据.因此,它弥补了单一测量方式的不足(隧穿或者约瑟夫森).图10(f) 展示了基于该方案的测量结果 (利用退卷积从电导谱变换到态密度谱),可以清晰地观察到存在几条不同透射率的ABSs 能谱.另外,利用得到的能谱还能进一步提取CPR,并与基于极不对称结 (调整结区大小或调节栅极电压) 的测量结果进行比较,从而实现多种测量结果的交叉验证.

5 总结与展望

MZM 遵从非阿贝尔统计,这是利用其实现拓扑量子计算的基础,而拓扑超导则被认为是MZM的理想载体.目前,已经在本征拓扑超导和人工拓扑超导研究方面取得了许多令人振奋的进展.在实验上,人们利用输运手段已经观察到了稳定的ZBCP、马约拉纳振荡、超导岛单电子库仑阻塞谱、分数约瑟夫森效应、非正弦的CPR 等与MZM 相关的特征,这为进一步利用编织操作确认其非阿贝尔统计性质打下了基础.此外,研究MZM 的输运手段与当前的半导体制程工艺相兼容,这为今后构建拓扑量子比特,搭建通用量子计算机提供了技术支持.

尽管人们已经观测到与MZM 相符的诸多输运行为,但不容忽视的是,当前探测MZM 的实验结果还存在拓扑平庸的解释.为了得到更加可靠的MZM 信号,实验上需要同时进行多种测量手段来相互佐证.这类实验包括: 同时对纳米线两端进行隧穿探测[84,88,209]、隧穿谱和库仑阻塞谱的联合探测[177]、三端器件的电导矩阵探测[183,184]以及约瑟夫森器件上的隧穿探测[208,210]等.同时,实验上还需要对已有的测量手段进一步优化.譬如,在接触式探测实验中,探测电极的引入会增强准粒子中毒过程,对MZM 的实现和探测都十分不利[211,212].为此,可以利用非接触式的实验方案来代替接触式测量,包括约瑟夫森超流谱[213]、微波谱[31,214-216]、扫描SQUID 显微谱[217,218]和快速电荷感应测量[219,220]等.另外,传统的低频探测手段很容易受到准粒子中毒的影响.因此,借鉴超导量子比特的高频测量有望获得更加可靠的特征信号[221-223].

选取2017年2月～2018年8月进行冠脉PCI术的心房颤动患者72例作为研究对象，以随机分配法将其划分为实验组与对照组。其中，实验组男20例，女16例，平均年龄（60.3±5.8）岁，存在高血压与高脂血症疾病各16例，8例存在糖尿病，充血性心衰与甲状腺功能异常各4例，2例存在外周血管性疾病；对照组男19例，女17例，平均年龄（60.5±5.6）岁，16例存在高血压，15例有高脂血症，8例存在糖尿病，5例有充血性心衰，4例为甲状腺功能异常，存在外周血管性疾病者2例。对两组患者一般资料比较，差异无统计学意义（P＞0.05）。

当实验上确定了MZM 的存在之后,人们需要通过编织实验来验证其非阿贝尔统计性质.理论上已经提出了多种编织MZM 的方案,如约瑟夫森三结[15]、三结纳米线[224]、磁通涡旋编织[6]以及手性边缘模编织[225]等.利用这些编织方案可以构建受拓扑保护的量子门操作,结合基于MZM 的拓扑量子比特,最终有望实现容错的拓扑量子计算.