基于机器视觉的图像高维特征智能提取算法

李明磊，赵俊杰，李 翔

（1.中信戴卡股份有限公司，河北秦皇岛 066011；2.广州引力波信息科技有限公司，广东广州 510000）

高维特征能够反映出目标图像中像素节点的分布形式，在进行参量提取的过程中，能够提供大量的可参考信息。然而，随着原始图像存储空间的不断增大，所选定投影向量与真实向量之间的差值水平也会逐渐增大，这就会对主机元件准确提取图像高维特征参量造成较大压力[3]。以3D 轮毂模型为例，改进SIFT 提取方法虽然能够准确定义投影向量的长度值水平，但却并不能将其取值结果控制在既定数值区间之内，这就使得投影向量与真实向量之间的差值水平始终难以得到有效控制[4]。

为解决上述问题，引入机器视觉技术的应用思想，并以此为基础，设计一种新型的图像高维特征智能提取算法。

1 基于机器视觉的图像特征匹配

1.1 视觉坐标系

图像的基础处理只能得到高维特征节点在二维空间内的像素坐标信息，而在机器视觉理论的认知中，线性摄像机模型反映的却是所选择特征节点的三维空间坐标信息，故而在实施图像特征匹配处理的过程中，应按照像素节点的三维分布形式构建视觉坐标系[5-6]。一个完整的机器视觉坐标系应同时包含X、Y、Z三个物理坐标轴，且坐标轴正方向的选取必须遵循像素点坐标由小至大的排列原则。具体的视觉坐标系求解表达式如下：

1.2 图像参数标定

图像参数描述了所选像素节点对于高维特征参量的承载能力。一般来说，为使机器视觉技术得到充分发挥，在选择标定节点时，应注重对其中所承载的高维特征参量进行统计，尽可能将参量数值相近的节点归为一类，且一类像素节点的图像参数水平也必须保持一致[7-8]。设ε表示所选像素点的位置系数，xε、yε、zε分别表示该像素点坐标在X轴、Y轴、Z轴方向上的数值分量，δx、δy、δz分别表示X轴、Y轴、Z轴方向上像素参量的初始赋值，可将基于机器视觉的图像参数标定表达式定义为：

为避免所选像素点与视觉坐标系源点重合，在求解图像参数时，要求系数ε的取值不能等于0。

1.3 线性摄像机模型

线性摄像机模型决定了机器视觉技术的实际作用能力，对于图像高维特征提取任务而言，独立线性摄像机模型中所包含的高维特征参量种类越多，主机元件在执行提取指令时所具有的选择空间也就越大，在此情况下，所获得的参量提取结果也就越符合实际应用需求[9]。由于图像高维特征参量的分布状态并没有明显的规律性，所以在建立线性摄像机模型时，还需对既定节点在X轴、Y轴、Z轴三个方向上的数值分量进行综合考虑。设ex表示图像高维特征参量在X轴方向上的数值分量，ey表示Y轴方向上的数值分量，ez表示Z轴方向上的数值分量，线性摄像机模型表达式为：

式中，β表示视觉坐标系中的像素特征提取系数，φ表示图像高维特征在视觉坐标系中的布局系数。在机器视觉技术的约束作用下，只有线性摄像机模型对于图像高维特征参量的容纳能力足够强，最终所得的图像特征提取结果才能够符合实际应用需求[10]。

2 图像高维特征智能提取

2.1 尺度空间金字塔的构建

尺度空间金字塔是一种行为标准，能够按照既定顺序将待处理图像特征参量排列起来，从而避免投影向量之间出现相互遮挡的情况，实现对所得向量与真实向量之间长度差值水平的有效控制[11-12]。在图1 所示的尺度空间金字塔模型中，视觉坐标系的数值容纳能力最强，这就表示所有待提取图像特征参量的定义形式都必须满足视觉坐标系的划分标准。

11月5日，国家主席习近平出席首届中国国际进口博览会开幕式并发表题为《共建创新包容的开放型世界经济》的主旨演讲，强调：回顾历史，开放合作是增强国际经贸活力的重要动力；立足当今，开放合作是推动世界经济稳定复苏的现实要求；放眼未来，开放合作是促进人类社会不断进步的时代要求。各国都应该积极推动开放合作，实现共同发展，开创人类更加美好的未来。中国推动更高水平开放的脚步不会停滞，推动建设开放型世界经济的脚步不会停滞，推动构建人类命运共同体的脚步不会停滞。

图1 尺度空间金字塔的结构简图

设s表示图像高维特征参量的纵向排列系数，γ表示横向排列系数，表示图像尺度向量均值，ι1、ι2表示两个不相等的空间标记向量。联立上述物理量，可将图像高维特征的尺度空间金字塔表达式定义为：

尺度空间金字塔模型不但可以对图像高维特征参量进行重排处理，还可以保证待运算数据的收敛性能力。

2.2 高维特征提取

对于图像高维特征参量而言，由于不同信息所属的层级类别不同，所以与之相匹配的收敛性条件也就有所不同。简单来说，收敛特性是处理主机判定图像高维特征参量所处层级组织的关键条件，在机器视觉理论的影响下，收敛性强的图像高维特征参量在尺度空间金字塔中所对应的存储位置也就相对较高；反之，若图像高维特征参量的收敛性能力较弱，就表示其在尺度空间金字塔中所处的存储位置也就相对较低[13-14]。

设i表示高维特征，r表示低维特征，且两者的初始取值都等于自然数1，可将图像高维特征提取模型表示为：

式中，di表示高维存储向量，dr表示低维存储向量，f表示图像特征分辨系数，表示收敛性指征。随着待处理图像高维特征参量赋值条件的改变，复杂度智能参量表达式的求解结果也会不断发生变化。

2.3 复杂度智能参量

复杂度智能参量是一项矢量化指标，可以根据图像高维特征节点的收敛特性，判断当前所执行的机器视觉复原机制是否能够满足提取特征参量指征的处理需求[15-16]。

在尺度空间金字塔框架结构中，待复原图像高维特征参量的收敛性能力越强，相邻参量节点之间的映射关系也就越明显，在此情况下求解所得的复杂度参量指标也就越能反映出图像高维特征参量的实际排列形式。设c1,c2,…,cn表示n个不同的图像高维特征智能参量节点定标值，g表示基于机器视觉复原机制的特征映射系数。在上述物理量的支持下，可将复杂度智能参量表达式定义为：

在复杂度参量的支持下，按照机器视觉复原机制的执行标准，对相关系数指标进行处理，完成图像高维特征智能提取算法的设计与应用。

3 实例分析

3.1 实验准备

选择轮毂结构作为实验对象，利用图2 所示3D视觉软件对其进行复原处理。在复原后图像中选择八个连接轴作为监测向量，分别利用实验组、对照组方法，对监测图像高维特征进行提取处理。

图2 3D轮毂的视觉复原图像

3.2 数据分析

投影向量与真实向量之间的长度差值能够反映出所选监测方法对于图像高维特征的提取能力。在不考虑其他干扰条件的情况下，投影向量与真实向量之间的长度差值越小，表示所选监测方法对于图像高维特征的提取能力越强。

表1 为3D 轮毂连接轴真实向量长度及其投影向量的理想长度数值。

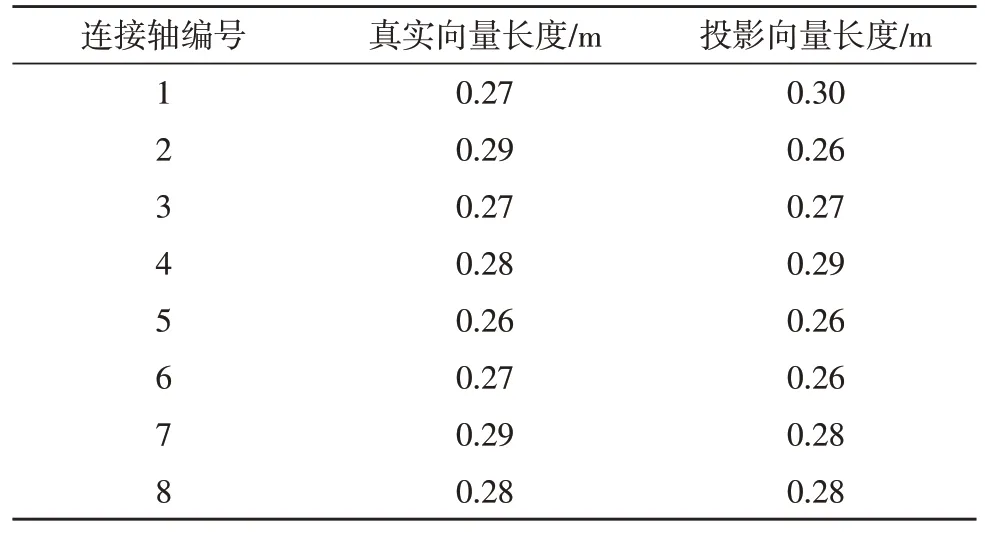
表1 3D轮毂连接轴数值

利用表1 数据，对比在实验组、对照组提取算法作用下3D 轮毂连接轴投影向量的长度数值，测试结果如图3 所示。

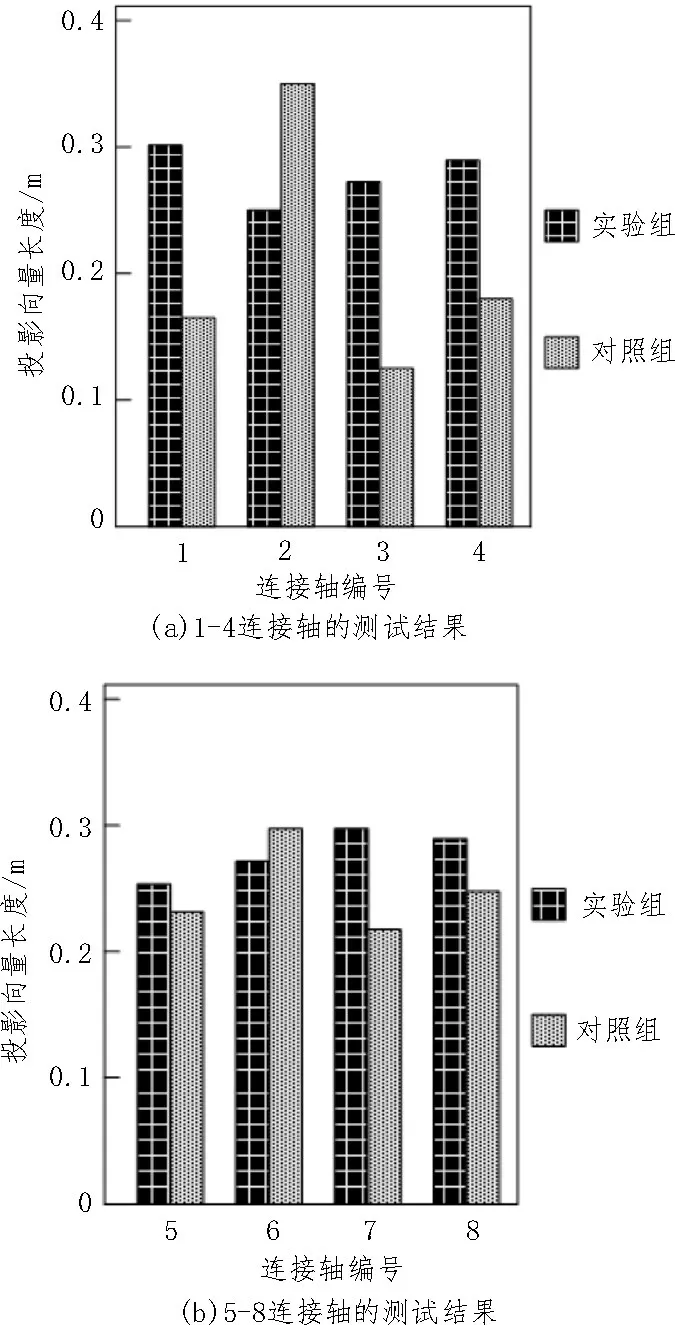
图3 投影向量的对比测试

根据图3 的测试结果可知，3D 轮毂连接轴真实向量长度均值为0.276 3 m，该文方法下3D 轮毂连接轴投影向量长度均值也为0.275 0 m，与真实向量长度下相差不大，相比之下，对照组发3D 轮毂连接轴投影向量的长度与真实情况出现较大偏差，说明该文方法应用效果较优。

综上可知，对于3D 轮毂模型而言，随着机器视觉技术的应用，所选监测对象投影向量与真实向量之间的差值水平得到了有效控制，与改进SIFT 的提取方法相比，更符合准确提取图像高维特征的实际应用需求。

4 结束语

在改进SIFT 提取方法的基础上，新型图像高维特征智能提取算法按照机器视觉理论的实践标准，对图像参数进行标定处理，又根据尺度空间金字塔建立原则，判断图像高维特征的收敛特性，从而得到准确的复杂度参量指标计算结果。在实用性方面，随着机器视觉理论的应用，图像投影向量与真实向量之间的差值水平可被控制在0.01 m 左右，在准确提取图像高维特征方面能够起到较强的促进性作用。