“三式”复习样态 实现深度学习

陈洪

有效的数学复习课应该是建立在尊重学生已有认知的基础上，从学生已有的知识水平出发，顺应学生学习规律而实施的课堂。教师应该建设一种让学生期待的复习模式，即设置一些综合性强，以及需要学生调动相关知识进行思考、整理的数学问题，促进学生的知识库存有效运转，形成户枢不蠹的“能源”。同时，促使学生学习动力被有效激发，学生充满张力地抓住“核心问题”，顺理成章地理顺“核心关系”，水到渠成地建立“核心结构”，在复习课上展开深度学习，提升复习效率。

一、提纲挈领式的问题导入，直面“核心问题”

众所周知，问题能够引导学生探究，教师在数学复习课上设置的问题必须精炼、重点突出，并富有思考性。一经抛出就要有能引发学生追寻答案的强烈兴趣，促进学生主动探究，实现“一石激起千层浪”的效果。

例如，在六年級总复习课中复习与“平面图形面积”相关的内容时，通常是先对面积计算公式进行复习后再展开系列复习活动，学生们按部就班地进入程序性复习历程，这样的复习课并不能激起学生积极思考的兴趣。其实同样的复习内容，笔者认为可以在课的起始阶段就抛出算式6.28×2，并直接推出问题：“你能想起哪些平面图形的面积可以通过这个算式来计算呢？”通过这样诱导式的复习问题，激发学生积极搜寻相关图形面积的计算方法，特别是圆的面积公式，为后续的问题作准备。学生通过对问题的讨论，汇报了可以符合该算式的各种平面图形的面积计算，如长方形、三角形、平行四边形等。教师提出：“刚才大家所说的是平面图形中最基础的知识。现在再回头看看，为什么这些图形的面积都可以用6.28×2来计算？”从此问题出发去复习公式的推导过程，引导学生思考：“是否也可以通过看起来比较复杂的梯形面积计算公式反向推导出像长方形这样简单的图形面积计算公式呢？”教师组织小组合作探究，通过尝试推导、交流沟通后，学生出现了以下见解：（1）我们可以将梯形下底中的一个顶点向内移动，这样下底b慢慢变小，当下底减小到跟上底a相等时，这时梯形就变形为平行四边形，再导入数据通过梯形面积计算公式推导得出平行四边形面积的计算公式S=ah；（2）继续移动下底b上的这个顶点，使下底的两个顶点完全重合了，这时梯形变成了三角形，再导入数据通过梯形面积计算公式推导出公式S=ah÷2；（3）假设梯形为直角梯形，当我们移动下底的顶点（非直角边上的顶点），让下底逐渐变短，变成和上底一样长的时候，它就变成了一个长方形，通过梯形面积计算公式推导出公式S=ab（此处b为梯形的高）；（4）在上述步骤（3）的基础上很容易通过长和宽相等的数据导入公式，推论正方形的面积计算公式就是S=a2，教师应注意此处应引导学生思考：“理论上，这里可以推论出正方形的面积计算公式，但是从‘6.28×2算式出发可行吗？为什么？”让学生用正方形边的特性否定算法的可行性；（5）教师再次提出问题：“想一想，圆可否从梯形出发顺利推导出来呢？”大部分学生认为不太可能实现。此时，插入微课“出入相补的梯形”动态演示变化过程，教师把等腰梯形平均分成若干个等腰三角形（三角形的高等于梯形的高），当分成的等腰三角形个数足够多、足够小时，再拼补成圆，最后通过梯形面积公式推导，得出公式：S=πr2。

由此可见，基于学生的知识基础，用提纲挈领式的问题能帮助学生展开深度学习，让学生学会主动探究，自主回忆学习活动中运用到的知识内容，将教师提供的问题变成提升学生自主思考能力的“原料”，用追根溯源的方式，直面“核心问题”，提升复习课的效果。

二、抽丝剥茧式的活动过程，理顺“核心关系”

通常组织一节复习课教师要提供许多复习材料，让学生逐题思考演练，但这种方式往往收效甚微，学生甚至根本不明白各项材料之间的关联，无法掌握复习的要领。这就需要教师精挑细选，合理提炼材料之间的关系，让学生面对材料能展开有效的思考，合理整理自己原有的知识“库存”。

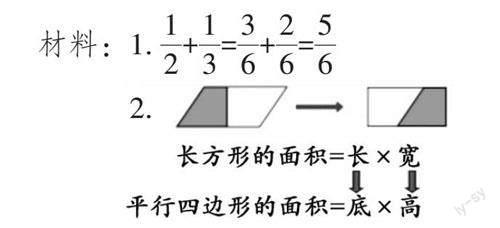
在六下期末复习阶段可以设计这样一节课“转化”。课的开始就用课件演示一份材料（如下图），教师提出相关要求：“（1）找出材料1和材料2之间的共同点，并请你提供类似的数学材料。（2）你能否用适当的语言将这份学习材料所能提供的数学信息表达出来？”学生通过讨论，明白材料中异分母加减法的计算方法与平行四边形的面积公式推导二者都隐藏着重要的数学思想——转化，随着学生举出的例子越来越多，他们也深刻体会数学知识学习过程中转化思想运用的普遍性。此时，教师趁热打铁追问：“同学们想一想，在这些知识的学习过程中所运用的转化思想可以分成几类？”促使学生往深处去思考，由此得出：数与数、形与形、数与形三类转化方式。至此，学生在教师的引领下不知不觉地进入“卷入式”的学习空间，展开对知识抽丝剥茧式的“深加工”，实现对数学方法的深入复习。

材料：1. [12]+[13]=[36]+[26]=[56]

2.

三、自主反思式的课堂总结，建立“核心结构”

数学向来都被定义为结构的科学，所以笔者以为，站在教育生态学、教育心理学的角度审视数学课堂生态结构，良好的课堂总结有助于课堂教学活动的开展，并能紧扣数学知识的核心结构。良好的课堂总结应具备立足教材，基于学生知识基础等要素，让学生徜徉于知识学习的过程中，不断思索、善于反思，能够逐渐自主建构相应的数学知识体系。

所谓知识的建构，就要让学生通过纵向联系建立长程的知识链条，从整体上把握知识构成。例如，与长度、面积、体积相关的度量单位的学习虽然被分散在不同的年级，却具有知识结构的一致性。因此，教学时必须组织学生参与单位标准的建立，体验单位累积的过程。因此，笔者认为面对这一系列知识点的教学时，必须要抓住“种子课”，舍得花大力气上好它。以“立体图形体积”的复习教学为例，可让学生借助数格子的方法回顾面积的大小其实就是面积单位的累加，链接整数乘法的意义，得出长方形的面积=长×宽；继续通过数小正方体的方法回顾长方体的体积计算方法，再链接整数乘法的意义得出长方体的体积=长×宽×高。再组织学生展开想象：“只要符合什么条件的立体图形就能用V=sh来计算？”这一系列看似简单的复习过程，学生已在潜移默化中体验了转化的思想在几何知识学习中的应用。最后，教师追问：“请你简要地说一说图形的面积和体积的学习有什么异同点。”让学生自主追溯圆面积的转化—平行四边形面积的转化—长方形的面积（长方体的体积），最后回归长方形面积的计算方法——数格子。这样在教学过程中，学生不仅能自主地将单一的知识点归入自我已有的知识体系中，还在学习的过程中潜移默化地感受转化思想在数学学习中的强大功用，让数学思想方法渗入脑海。

（作者单位：福建省闽侯县实验小学 责任编辑：宋晓颖）