长河坝水电站特高心墙堆石坝双防渗墙渗流控制特性反演分析
王相烜,刘得潭,何传凯,张志银,黄章鑫,徐力群
(1.四川大唐国际甘孜水电开发有限公司,四川 康定 626001; 2.大唐水电科学技术研究院有限公司,广西 南宁 530007; 3.河海大学水利水电学院,江苏 南京 210098)
土石坝工程的渗流控制特性对其安全稳定运行至关重要[1-2],为保证土石坝渗流安全稳定,众多学者对土石坝渗流问题进行了诸如监测资料分析、防渗系统方案比选与优化设计、数值计算模型参数确定、影响因素敏感性分析等一系列研究。宋锦焘等[3]引入正态分布和瑞利分布函数描述库水位和降水量对土石坝渗流滞后的影响,同时采用智能算法求解模型参数,构建符合监测资料的渗流监控模型。王硕等[4]在保证某电站首部枢纽工程年渗漏量小于坝址多年平均径流量5%的前提下,通过方案比选,提出了减小防渗帷幕一定深度以及缩短左右岸灌浆洞长度的设计优化方案,可有效降低防渗系统建设成本、缩短建设工期。王学武等[5]研究了覆盖层上高土石围堰防渗墙的设计深度,指出仅增加防渗墙深度并不经济,建议对左右岸岩体进行帷幕灌浆。Tan等[6]利用人工智能算法IPSO反演得到了包括防渗帷幕在内的面板坝各分区材料的渗透系数。岑威钧等[7-8]分别计算分析了防渗墙深度、覆盖层深度和渗透性对土工膜防渗堆石坝渗流场的影响。Zhang等[9]以华阳河上一个土石坝为例,研究了渗漏量对防渗帷幕的深度和长度以及石灰岩层的渗透系数的敏感性。甘磊等[10]计算分析了土工膜不同缺陷位置、缺陷孔径对膜下压力水头以及渗漏量的影响。
垂直防渗作为发展比较成熟的技术,在土石坝坝基覆盖层防渗中被广泛应用,其主要形式有混凝土防渗墙、灌浆帷幕和其他材料防渗墙等,同时,一些工程采用2道防渗墙防渗[1]。目前,针对双防渗墙形式的研究集中在应力变形方面[11-13],渗流特性方面研究较少,且以单因素敏感性研究为主。徐颖等[14]针对瀑布沟砾石土心墙坝,研究了主、副防渗墙不同渗透系数组合以及墙下不同帷幕深度组合对坝基渗流场的影响。王正成等[15]通过物理试验,研究了渗流量和出逸坡降在双防渗墙不同深度组合以及不同间距下的变化。然而,单因素敏感性分析难以比较各因素间的敏感性强弱,因此可以通过设计正交试验,实现多因素敏感性分析。目前,基于正交试验的多因素敏感性分析方法在水利工程的结构、渗流等研究中被广泛使用[16-20],这些研究均为合理选择各自模型参数提供了重要依据。
长河坝砾石土心墙堆石坝坝址处覆盖层最厚达79.3m,设计中采用2道全封闭混凝土防渗墙进行坝基防渗[21]。双防渗墙相较于单防渗墙存在分担阻挡水头的现实问题,长河坝水库蓄水后,大坝主防渗墙阻挡水头比例远大于设计阶段的计算值。为更有目的性、针对性地反演材料渗流参数,本文将基于正交试验的多因素敏感性分析法应用于长河坝双防渗墙渗流控制特性研究中,定量判断各材料渗透系数敏感与否,分析各材料渗透系数对坝基主、副防渗墙承担水头比例的敏感性强弱;然后将敏感性分析成果作为材料渗透参数反演的依据,拟合坝基渗流场,以期能为双防渗墙工程渗流特性研究提供参考。
1 设计参数下长河坝渗流性态分析
1.1 工程概况
四川省甘孜州长河坝水电站位于大渡河干流上游金汤河口以下约4~7km河段。工程以单一发电为主,电站总装机容量2600MW(4×650MW)。水库正常蓄水位1690m,极限死水位1650m,正常蓄水位以下库容10.15亿m3,调节库容4.15亿m3,具有季调节性能。
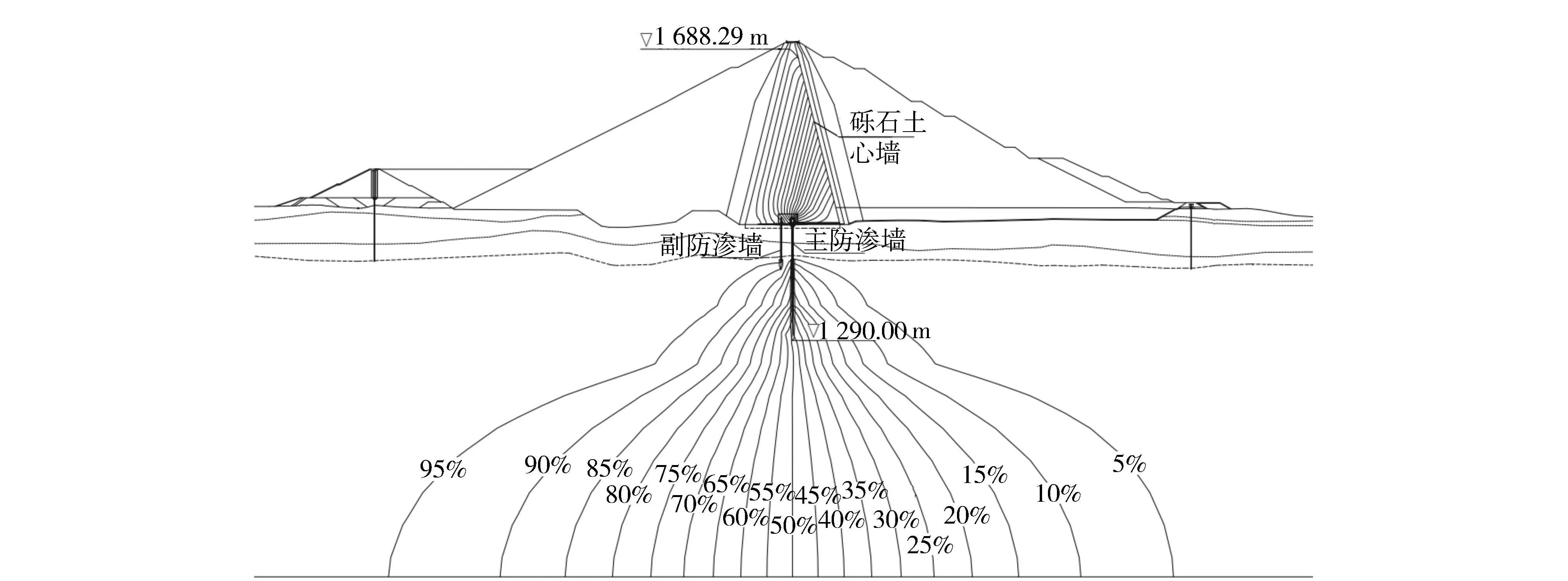
枢纽建筑物主要由拦河大坝、引水发电系统、泄洪洞和放空洞等组成。拦河大坝为砾石土心墙堆石坝,最大坝高240m,属特高坝,心墙与上、下游坝壳堆石之间均设有反滤层、过渡层,防渗墙下游心墙底部及下游坝壳与覆盖层坝基之间设有水平反滤层。覆盖层设置主、副两道全封闭混凝土防渗墙,主防渗墙布置于坝轴线平面,厚1.4m,副防渗墙位于主防渗墙上游,厚1.2m,两墙净距14m;覆盖层以下坝基及两岸基岩防渗采用灌浆帷幕防渗,主防渗墙下防渗帷幕伸入透水率小于等于3Lu的基岩不少于5m,副防渗墙下灌浆帷幕深度为30~40m,底部最低高程为1380m。大坝坝体典型剖面如图1所示。
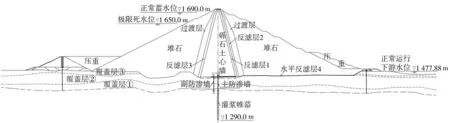
图1 坝体典型剖面
1.2 有限元模型
根据渗流分析的一般原则和计算要求,结合工程的结构布置图,构建三维有限元模型,如图2所示。模型左岸截取至(纵)0-449.0m断面,右岸截取至(纵)0+878.2m断面,库内上游边界截取至(坝)0-850.1m断面,河道下游边界截取至(坝)0+709.1m断面,底高程截取至建基面以下约2倍坝高处,底高程为972m。
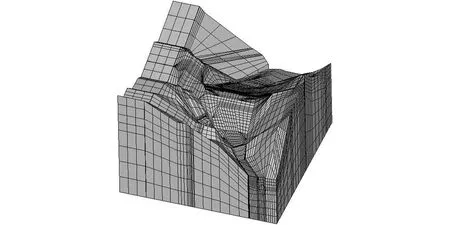
图2 三维渗流有限元模型
1.3 计算参数
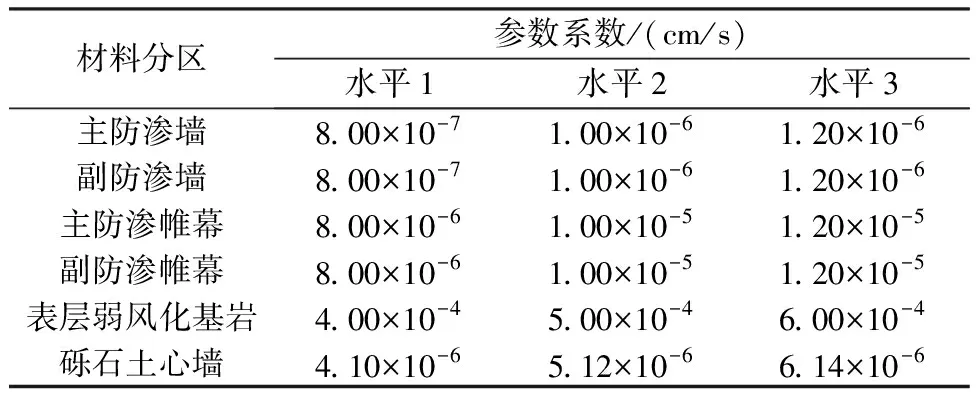
三维有限元渗流计算参数主要根据检测成果及地质提供参数建议值确定,防渗墙和防渗帷幕的渗透系数取其设计控制标准,各材料参数具体取值见表1。2021年9月20日至10月20日之间,库水位变幅较小,取该时间段的上、下游平均水位作为渗流计算的已知水头边界,分别为1688.29m和1477.93m。
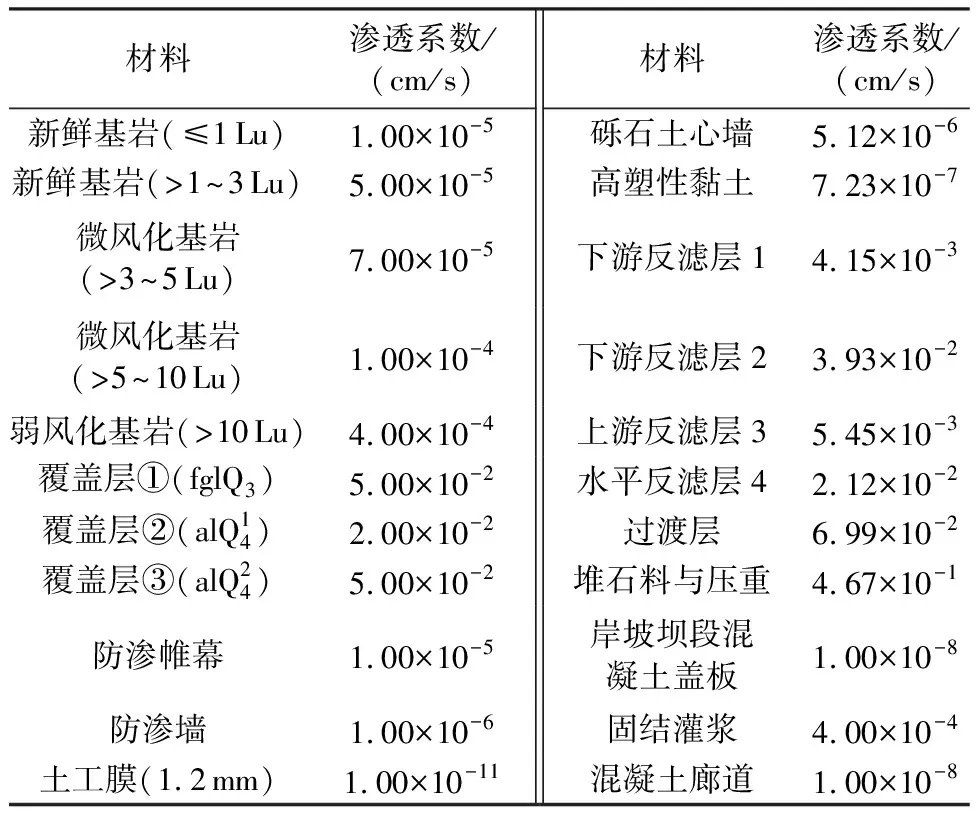
表1 坝基及坝体各分料区渗透系数
1.4 设计方案坝基渗流场分析
基于饱和-非饱和渗流理论,经有限元计算得到大坝渗流位势分布如图3所示,可以看到,副防渗墙与主防渗墙各阻挡约30%和70%的水头。
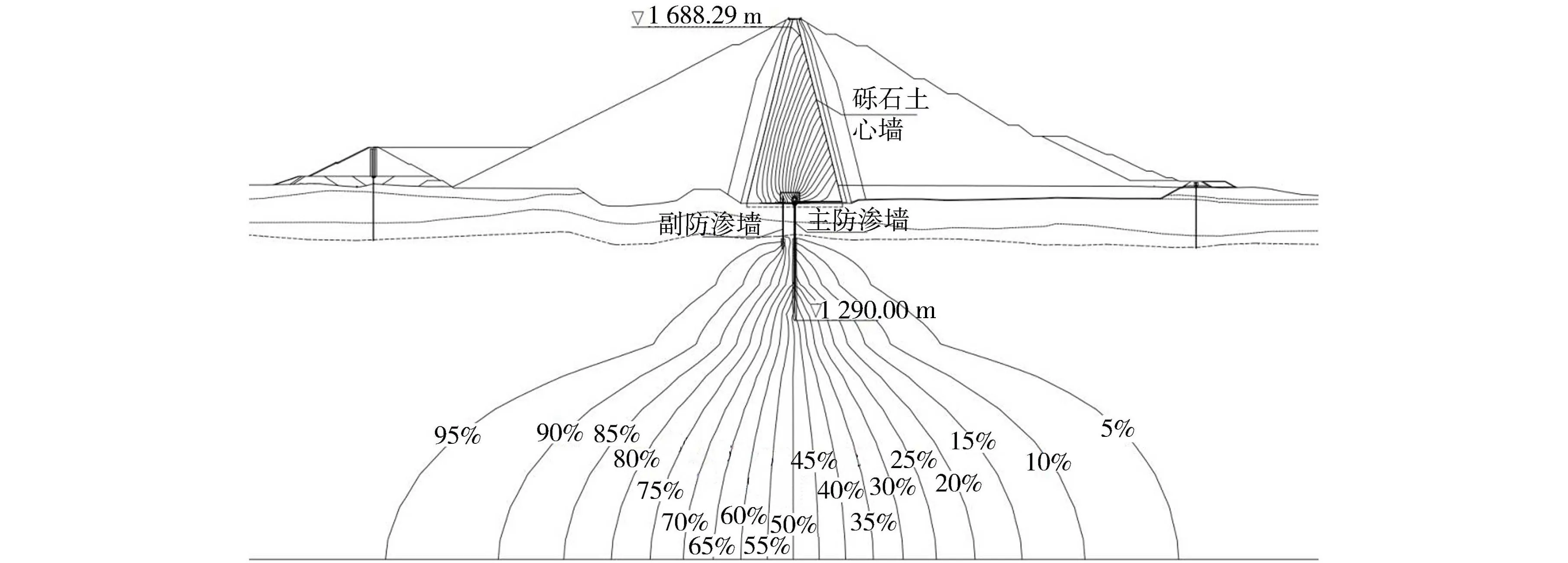
图3 设计方案最大断面渗流位势分布
1.5 现状监测资料分析
为判断大坝基础防渗系统的工作效能,安全监测设计在坝(纵)0+213.72m、(纵)0+253.72m、(纵)0+303.72m桩号每个监测断面主防渗墙后及主、副防渗墙之间各布置1支渗压计,各桩号测点编号及具体位置见表2。
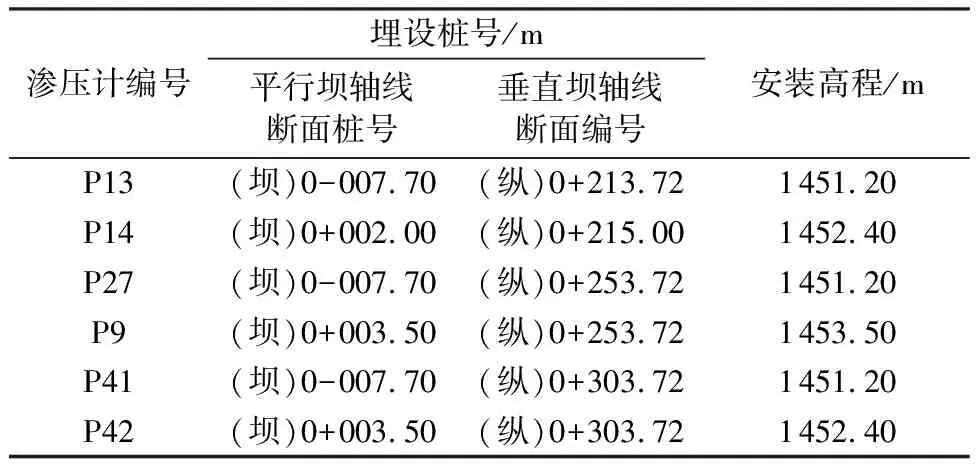
表2 坝基防渗墙渗压计安装位置
由图4可知,主、副防渗墙之间的渗压计(P13、P27、P41)测值在蓄水后出现了较大升高,且渗压水头基本受库水位控制;主防渗墙后的渗压计(P14、P9、P42)测值基本与下游水位相同,变化较小,说明大坝防渗系统整体防渗效果较好。2021年10月20日,在(纵)0+213.72m桩号,副防渗墙阻挡水头比例为12.89%,主防渗墙阻挡水头比例为86.61%;在(纵)0+253.72m桩号,副防渗墙阻挡水头比例为11.29%,主防渗墙阻挡水头比例为88.23%;在(纵)0+303.72m桩号,副防渗墙阻挡水头比例为10.43%,主防渗墙阻挡水头比例为88.92%。在设计阶段,防渗墙厚度主要根据其阻挡水头大小以及允许渗透坡降确定,主防渗墙实际阻挡水头高于设计方案计算结果,对其渗透稳定不利。
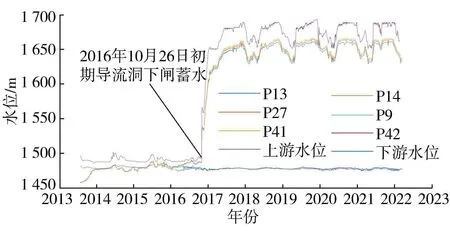
图4 坝基部分渗压计测值过程线
2 敏感性分析
2.1 敏感性分析原理
对于多因素的敏感性分析,因素水平数一定时,如果穷举试验方案,那试验方案将随影响因素数量的增加而呈指数形式增多,计算每一个方案不现实。正交试验则通过规格化的正交表挑选具有代表性的试验,使因素和水平均匀分散、整齐可比,可有效减少试验次数。正交表作为正交试验的关键,是根据正交原理设计的规范化表格,用Ln(rm)表示,其中,L为正交表代号,n为试验总次数,m为正交表的列数,即对试验指标可能有影响的变量个数,r为因素的水平数,即每个因素可能处的状态数。本文选用的L18(2×36)表示考虑7个变量,其中1个变量有2个水平(作为误差列),6个变量有3个水平(研究6个材料渗透系数的影响),共需做18次试验。正交试验结果的分析常采用极差分析法和方差分析法。
极差分析法作为一种直观分析方法,因计算简单易懂而在正交试验结果分析中被广泛使用[19]。其通过计算各因素的极差Rj判断因素的敏感性强弱,Rj越大,该因素对试验指标的影响越大。
极差分析时,并未将各试验方案结果间的差异分解为由因素水平变化引起的和试验误差引起的两部分,也无定量的标准判断该因素究竟敏感与否,而方差分析法可弥补这些缺陷[18]。方差分析法通过敏感性统计量Fj判断因素敏感性强弱。当Fj>F0.01时,认为因素j对指标有非常显著的影响;当F0.05≤Fj≤F0.01时,认为因素j对指标有显著的影响;当Fj (1) 其中 fj=r-1fe=r(q-1) 式中:Sj、Se分别为因素和误差的变动平方和;fj、fe分别为因素和误差的自由度;q为各水平重复的次数;xki为因素j在水平k下的第i次试验的结果。 本文研究大坝防渗系统各材料以及表层基岩的渗透系数对主、副防渗墙阻挡水头比例的影响,因此对三维有限元模型材料分区进一步细化,具体研究的材料共6个,分别为主防渗墙、副防渗墙、主防渗帷幕、副防渗帷幕、表层弱风化基岩(>10Lu)、砾石土心墙,其中,为方便表述,主、副防渗帷幕分别指主防渗墙平面的防渗帷幕和副防渗墙平面的防渗帷幕;设置3个水平,分别为0.8、1、1.2倍设计渗透系数(表3)。 表3 正交试验各因素渗透系数的水平取值 选择L18(2×36)正交表,并将2水平的第一列作为误差列,同时将表3中各因素的不同水平对应填入正交表内,计算得到各试验方案下主、副防渗墙阻挡的水头比例(表4)。 表4 正交试验方案及计算结果 表4中副防渗墙阻挡水头比例,由上游库水位Hup减去主、副防渗墙之间3只渗压计位置点处水头的平均值H1,再除以上下游水头差ΔH得到,即(Hup-H1)/ΔH,主防渗墙阻挡水头比例的计算同理。 以副防渗墙阻挡水头比例和主防渗墙阻挡水头比例共同作为指标进行极差分析,得到各因素在各水平下极差(表5)。各因素中对两道防渗墙阻挡水头最为敏感的是表层弱风化基岩的渗透系数,其极差达到0.174,主防渗帷幕渗透系数对该指标也较为敏感,极差为0.125;其余各材料渗透系数对该指标的敏感性较小,其极差均小于等于0.024。 表5 主、副防渗墙阻挡水头比例影响因素极差分析 以主防渗墙下游侧总阻挡水头比例作为指标进行极差分析,各因素的敏感性规律与以副防渗墙阻挡水头比例和主防渗墙阻挡水头比例共同作为指标的情况一致,材料渗透系数敏感性从强到弱依次为表层弱风化基岩、主防渗帷幕、副防渗帷幕、副防渗墙、主防渗墙、砾石土心墙,极差分别为0.348、0.250、0.048、0.030、0.015、0.013。 对主、副防渗墙阻挡比例和总折减水头比例这2种指标进行方差分析,计算得到各因素的变动平方和Sj、自由度fj和敏感性统计量Fj,如表6所示,敏感性规律与极差分析一致,材料渗透系数敏感性从强到弱依次为表层弱风化基岩、主防渗帷幕、副防渗帷幕、副防渗墙、主防渗墙、砾石土心墙。根据误差列自由度以及各因素的自由度查F分布表可知F0.01=98.50、F0.05=18.51,根据前文敏感性划分标准,表层弱风化基岩和主防渗帷幕对防渗墙阻挡水头比例有显著影响。 表6 主、副防渗墙阻挡水头比例影响因素方差分析 由于两道防渗墙对覆盖层进行了全封闭处理,防渗墙底部的防渗帷幕及基岩表层成为坝基绕渗的主要通道,而副防渗帷幕深度并未达到相对不透水层(透水率≤3Lu的基岩),主防渗帷幕伸入相对不透水层(透水率≤3Lu的基岩)不少于5m,因此表层弱风化基岩和主防渗帷幕对坝基渗流控制特性的影响最大,敏感性分析结果符合一般性规律。 根据敏感性分析,着重反演表层弱风化基岩与主防渗帷幕的渗透系数,同时调整副防渗帷幕以及主、副防渗墙的渗透系数,砾石土心墙则采用现场检测结果,最终确定的反演结果如下:主、副防渗墙的渗透系数分别为1.12×10-7cm/s和3.00×10-6cm/s,主、副防渗帷幕的渗透系数分别为6.99×10-6cm/s和2.79×10-5cm/s,表层弱风化基岩的渗透系数为6.23×10-4cm/s,最大断面位势分布如图5所示。经反演后参数计算,各渗压监测点的计算值与监测值之间的相对误差均小于5%,满足工程应用要求。 图5 反演后最大断面渗流位势分布 a.材料渗透系数对2道防渗墙各自阻挡水头比例的敏感性从强到弱依次为表层基岩、主防渗帷幕、副防渗帷幕、副防渗墙、主防渗墙、心墙,且表层基岩和主防渗帷幕有显著影响,其极差分别为0.174和0.125,敏感性统计量Fj分别为60.96和31.43,其余材料无显著影响。 b.在敏感性分析成果的基础上,有限元模型参数的反演更具有针对性和目的性,大大减小了反演工作量,反演计算结果中主、副防渗墙分别阻挡约90%和10%水头,计算值与测点实测值之间误差不超过5%,可满足工程应用要求。2.2 正交试验设计及计算成果
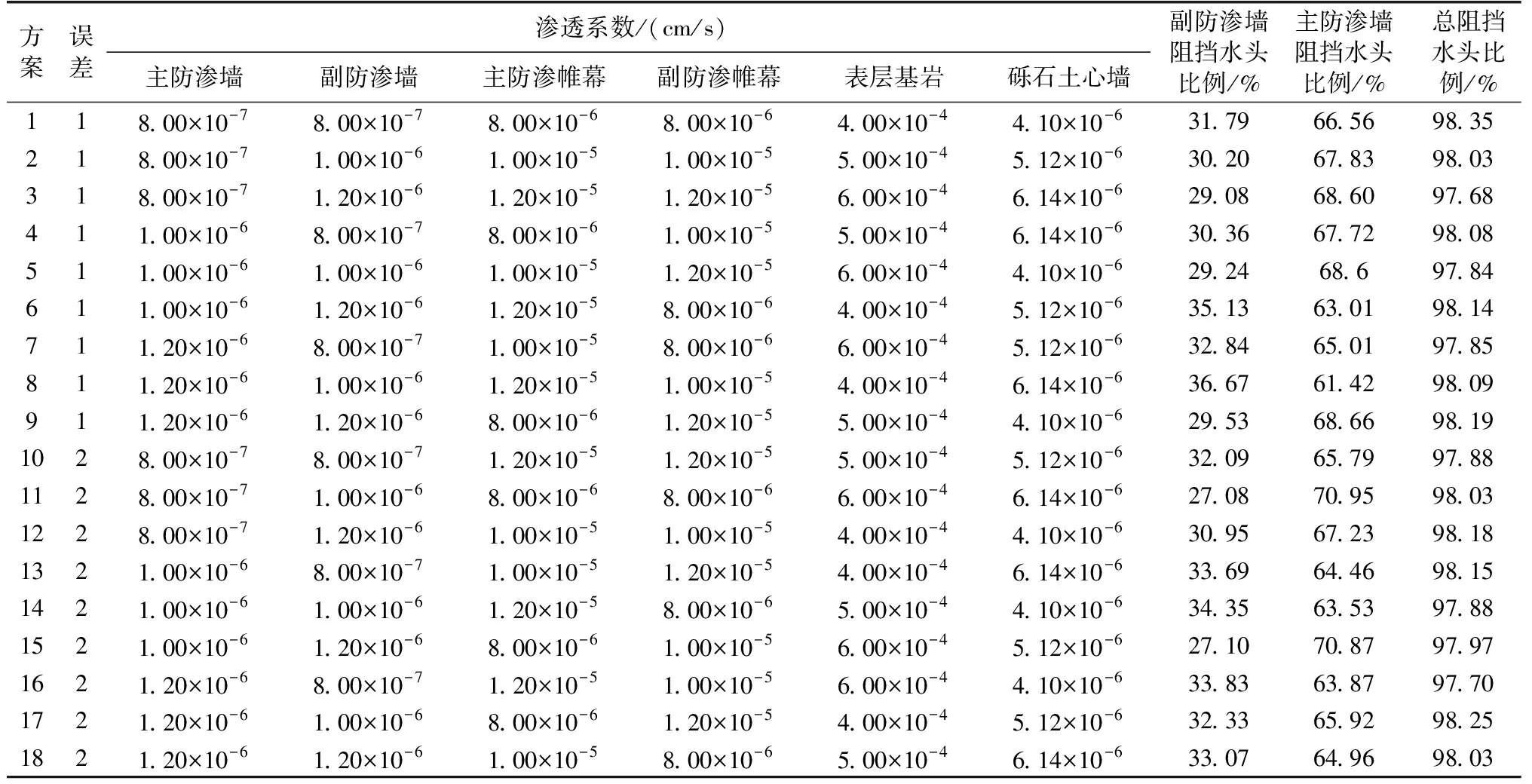
2.3 极差分析
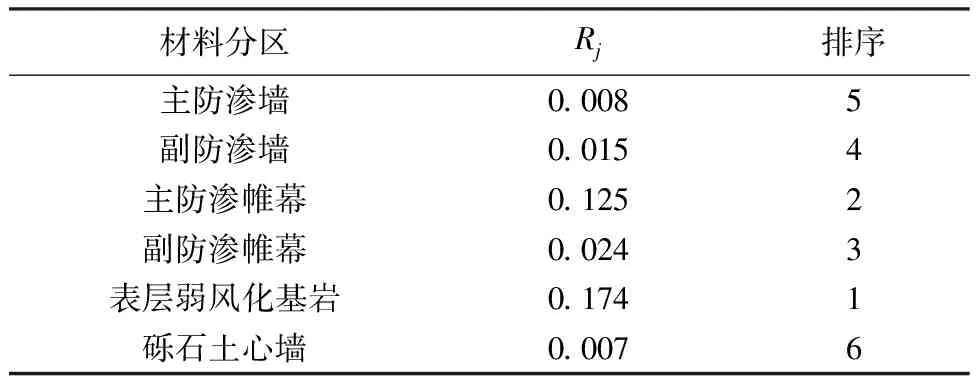
2.4 方差分析

3 模型参数反演结果
4 结 论

