GF(2m)域双参数ECDSA算法优化设计
方应李,方玉明
(南京邮电大学 集成电路科学与工程学院,江苏 南京 210023)
在数字签名方法中,文献[1~2]提出的基于离散对数的椭圆曲线密码体制具有更高的安全性,该密码体制得到了密码学界的重视与推广。文献[3]提出了经典的椭圆曲线数字签名算法(Elliptic Curve Digital Signature Algorithm,ECDSA),用户A使用私钥进行签名,用户B通过用户A的公钥对签名进行验签。签名算法中包括两次模逆、3次点乘以及若干次模乘运算。
文献[4]表明模逆运算的时耗是模乘运算的80倍。由于点乘运算中至少存在1次模逆运算,所以点乘运算是影响ECDSA安全性和效率的关键之处,因此业界学者集中研究点乘和模逆运算。文献[5]提出了无模逆运算的数字签名算法,简化了运算的复杂程度。文献[6]改进了模乘运算,提出了一种新的签名算法。虽然减少模逆运算可以提升签名效率,但也会引起伪造签名等安全性问题。因此,业界学者在改进签名效率问题的同时还应考虑到算法的安全问题。文献[7]提出一种高效的串行乘法器。文献[8]提出在二元爱德华曲线上进行标量乘。文献[9]提出了一种新的Itoh-Tsujii算法模逆算法,不仅提高了签名速度,且能更好地利用现场可编程门阵列硬件资源。
本文针对算法的时耗和安全性问题,提出了一种双参数ECDSA的改进方案,包括3次点乘和0次模逆运算,提高了算法的签名效率和安全性。权衡资源消耗与运算速度之后,本文提出一种基于二进制域的ECDSA的高性能实现方案。充分利用硬件并行优势[10],在模乘、模逆、点乘以及整体系统结构上进行了优化,取得了良好的效果。
1 双参数椭圆数字签名方案
1.1 数字签名算法描述
双参数ECDSA算法流程如图1所示。用户A选取随机数k、私钥d和椭圆上一点G,计算出消息M的签名信息(r,s,k1)。签名加密结束后,将公钥Q=dG、消息M以及签名信息(r,s,k1)一同发送给用户B。用户B进行签名验证后,通过对比计算结果判断签名是否成功。签名成功则说明消息M在传输过程未受到篡改;反之,消息M则被第三方攻击。
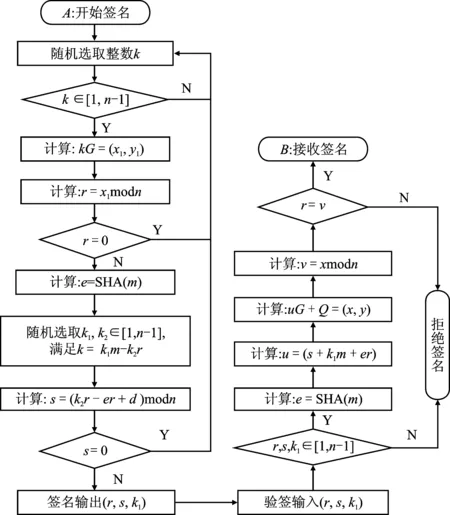
图1 双参数数字签名算法流程Figure 1. Flow of double parameters signature algorithm
式(1)可证明双参数ECDSA算法逻辑的正确性。
(1)
式中,r、s为签名信息;e为消息的离散值;d、Q为私钥和公钥;k、k1、k2均为随机数;G为椭圆上一点。
签名运算的耗时主要集中于模乘、模逆和点乘3种运算。由表1可以看出,新签名方案中没有模逆运算且仅使用了3次点乘运算,提高了签名效率。
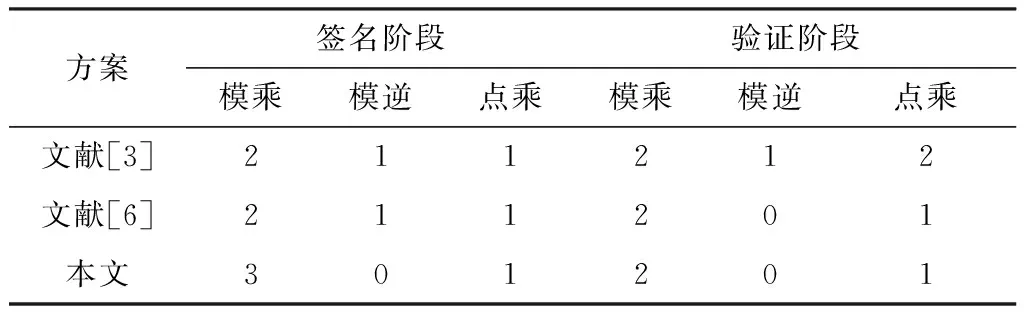
表1 签字方案效率对比Table 1.Efficiency comparison of signature schemes
1.2 椭圆曲线算法理论基础
通常在有限域上定义椭圆曲线,常用的有限域包括素数域GF(p)和二进制域GF(2m)。由于GF(2m)域中的运算无法进位,故更适合硬件实现。因此,本文选用GF(2m)域实现ECDSA算法,GF(2m)域上多项式基表示方法如式(2)所示
(2)
其中,ai∈{0,1}。
椭圆曲线加密体制的运算层次如图2所示。最上层的算法协议通过调用群运算层中的点乘(Point Multiplication,PM)、点加(Point Addition,PA)和倍点(Double Point,DP)实现。最底层为4种有限域模运算,是实现群运算层的基础。因此,实现椭圆曲线加密的高效设计需针对不同运算层次进行优化设计。
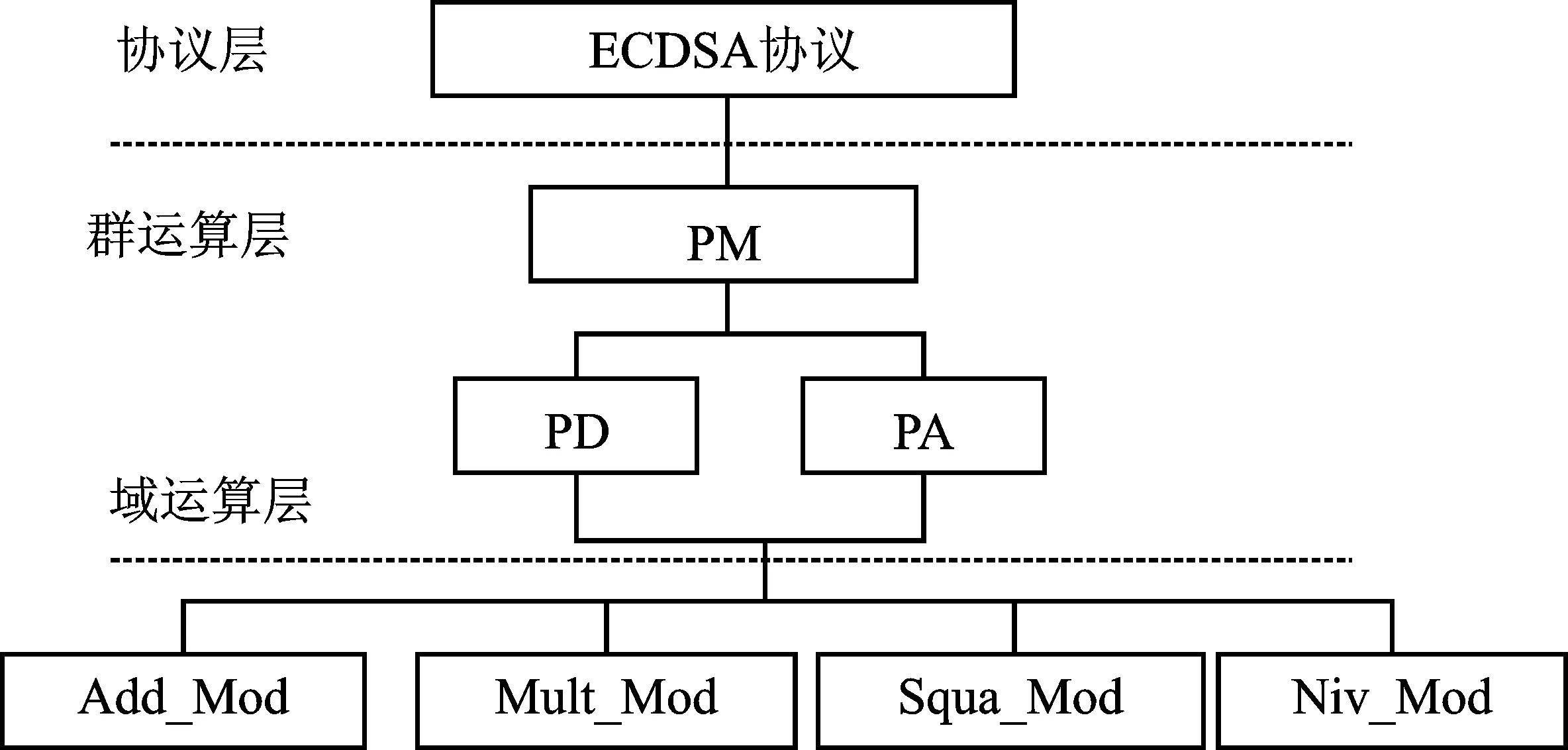
图2 椭圆曲线加密体制的运算层次Figure 2.Operation level of elliptic curve encryption system
2 运算模块的优化设计
2.1 域运算优化设计
本文选用233位域宽的GF(2m),对应的不可约多项式F(x)如式(3)所示。GF(2233)域上的模加运算通常使用异或运算来完成,对应的硬件电路可以利用233个异或门进行实现。
F(x)=x233+x74+1
(3)
2.1.1 模乘运算设计
模乘运算是影响点乘运算效率的关键之处,包括多项式乘法和模约减运算两个步骤。本文提出基于移位相加和异或运算的串并混合快速模乘运算,主要步骤如下所示:
步骤1输入A(x),B(x),C(x)∈GF(2233);
步骤2模乘值的初始化,C(x)=0;
步骤3将233位宽的数据A(x)分段,如
A(x)={a7,a6,a5,a4,a3,a2,a1,a0}
(4)
步骤4进行8轮乘法和取模运算,具体为
C(x)=aiB(x)+C(x),i∈[0,7]
(5)
如果C232=0,则C(x)保持不变;反之,C232=1时,C(x)执行式(6)取模运算;
C(x)=C(x)⊕F(x)
(6)
步骤5输出A(x)和B(x)的模乘值C(x)。
本文提出的串并混合快速模乘运算流程如图3所示。将输入多项式数据A(x)分为8段32位的子数据,最后一段32位子数据通过补零实现。每个时钟进行一次32位的移位相加和取模运算。可以看出,需要(232/32)+1个时钟便可完成一次模乘操作。
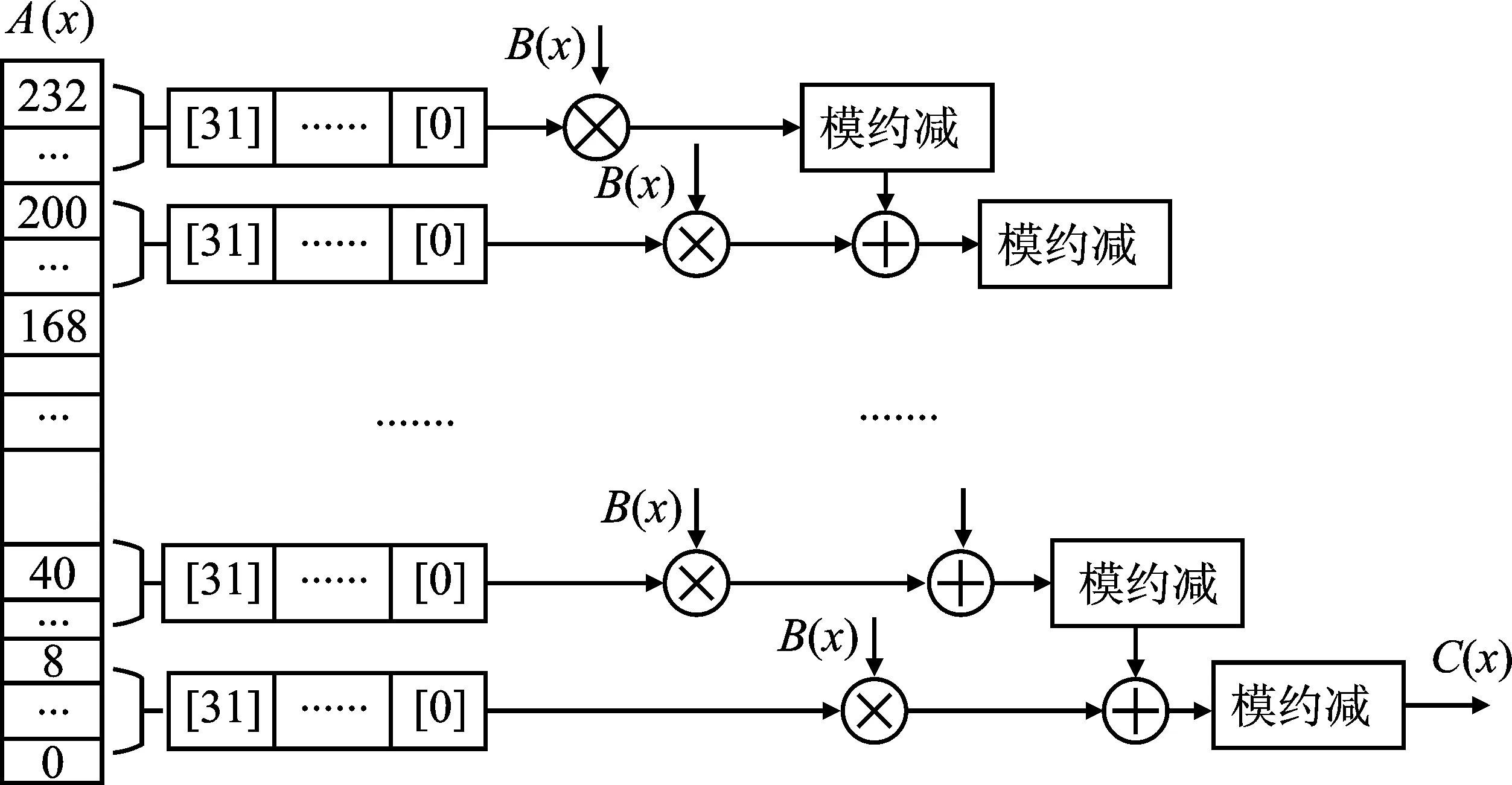
图3 串并混合快速模乘运算Figure 3. Serial parallel hybrid fast modular multiplication
2.1.2 模平方运算设计
模平方运算是两个相同数的模乘运算。由于模乘运算耗时大且硬件电路复杂,因此本文提出基于GF(2233)域的快速模平方运算,从而提高了签名算法的效率。具体步骤如下所示:
步骤1输入多项式A(x)∈GF(2233)。
步骤2遍历i从0到73。若i为偶数,则执行式(7);若i为奇数,则执行式(8)。
C(i)=A[i/2]⊕A[196+i/2]
(7)
C(i)=A[117+(i-1)/2]
(8)
步骤3遍历i从74到147。若i为偶数,则执行式(9);若i为奇数,则执行式(10)。
C(i)=A[i/2]⊕A[196+(i-74)/2]
(9)
C(i)=A[117+(i-1)/2]⊕A[117+(i-75)/2]
(10)
步骤4遍历i从148到233。若i为偶数,则执行式(11);若i为奇数,则执行式(12)。
C(i)=A[i/2]
(11)
C(i)=A[117+(i-1)/2]⊕A[117+(i-75)/2]
(12)
步骤5输出A(x)的模平方值C(x)。
2.1.3 模逆运算设计
4种有限域模运算中最复杂和最耗时的是模逆运算,常用的模逆运算有基于欧几里德算法和费马小定理两种[11-12]。如式(13)所示,本文采用费马小定理将模逆运算转换为模乘和模平方运算,使用Itoh-Tsujii计算式减少模乘的次数。模逆运算的计算过程如表2所示。

表2 模逆运算过程Table 2. Modular inverse operation process
A(x)-1=A(x)2m-2
(13)
2.2 群运算优化设计
群运算是在椭圆曲线上使用两个点计算第3个点的过程,若两个点相同为PD运算,反之则为PA运算。群运算的计算过程只涉及点的横坐标,适合在硬件上实现。本文选择如式(14)所示的仿射坐标下的椭圆方程,为避免群运算中使用模逆运算,当Z≠0时,令x=X/Z且y=Y/Z,将式(14)转换为Lopez-Dahab(LD)投影坐标系下的方程,如式(15)所示[13]。
y2+xy=x3+1
(14)
Y2+XYZ=X3+Z4
(15)
ECDSA采用目前最流行的抗侧通道攻击的蒙哥马利点乘运算,包括初始化、主循环和坐标转换3部分[14]。主要步骤如下所示:
步骤1输入多项式k∈GF(2233)及椭圆上一点P(x,y)。
步骤2初始化坐标,将仿射坐标转化为LD投影坐标。遍历i从m-1到0,如果ki=1,则P1=(X1,Z1)=(x,1),P2=(X2,Z2)=(x4,x2)。
步骤3在主循环过程中一直调用PA、PD两个运算模块。遍历j从i-1到0,若kj=1,则P1=P1+P2,P2=2P2;反之kj=0,则P1=2P1,P2=P1+P2。
步骤4在坐标转换运算中存在唯一的模逆运算,将LD坐标转换仿射坐标。
X3=X1/Z1
(16)
(17)
步骤5输出仿射坐标系下的点乘坐标(X3,Y3)。
在主循环过程中,PA与PD之间的运算数值没有互相依赖。因此,本文采用部分并行PA和PD两种运算来提高PM运算的效率。根据如图4所示的并行运算流程,计算PA和PD的输入输出数据,如表3所示。
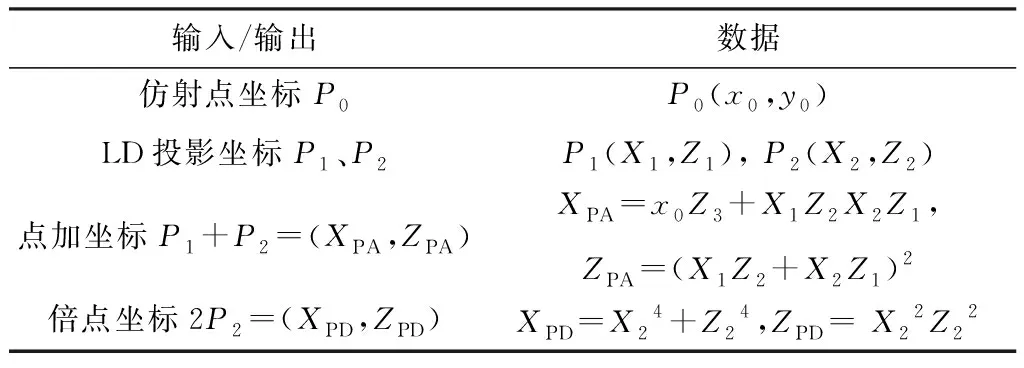
表3 PA、PD并行模型的输入输出Table 3.Input and output of PA and PD parallel models
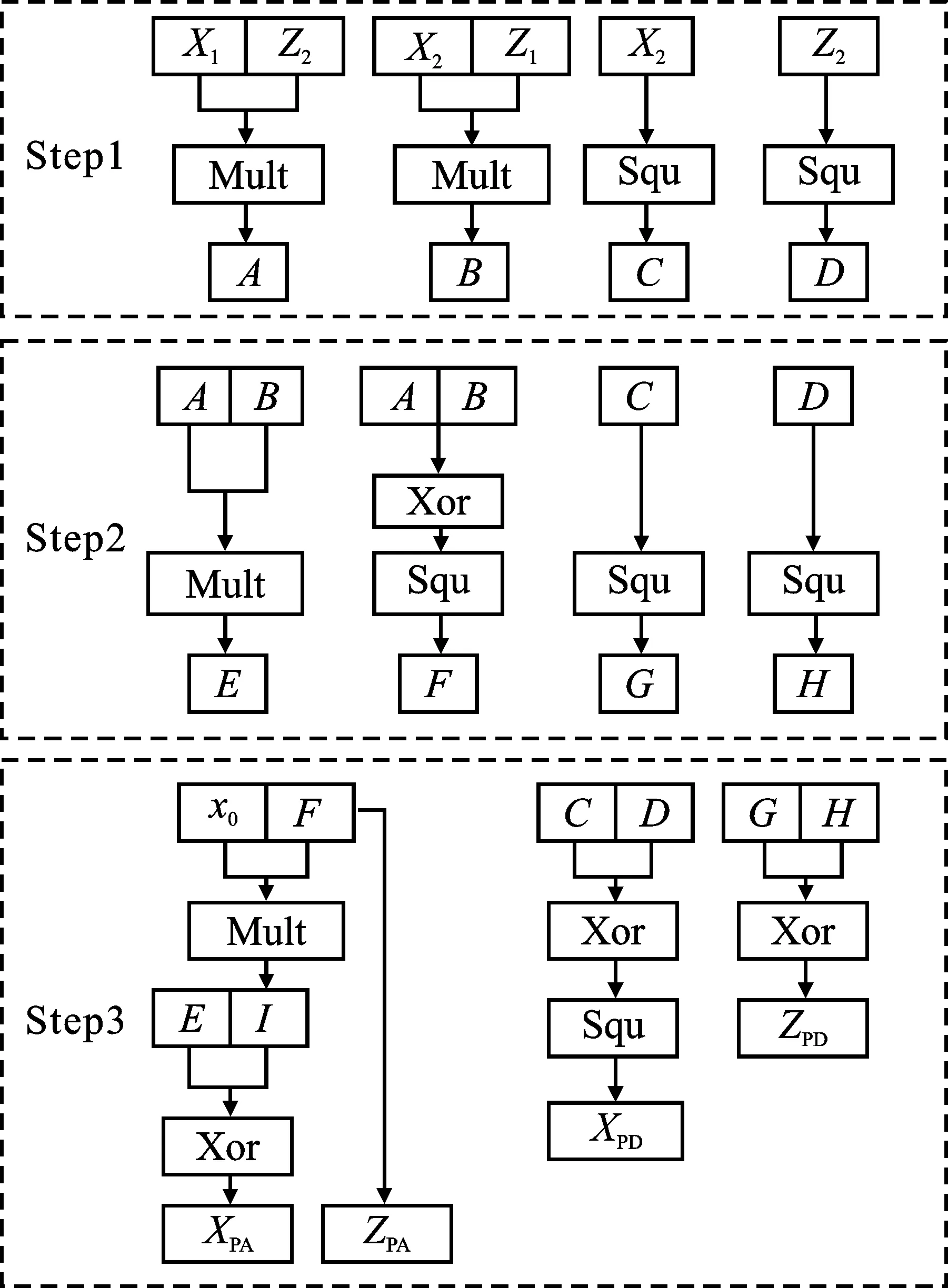
图4 PA和PD并行运算Figure 4. Parallel operation between PA and PD
3 双参数ECDSA方案仿真
3.1 加解密模型设计
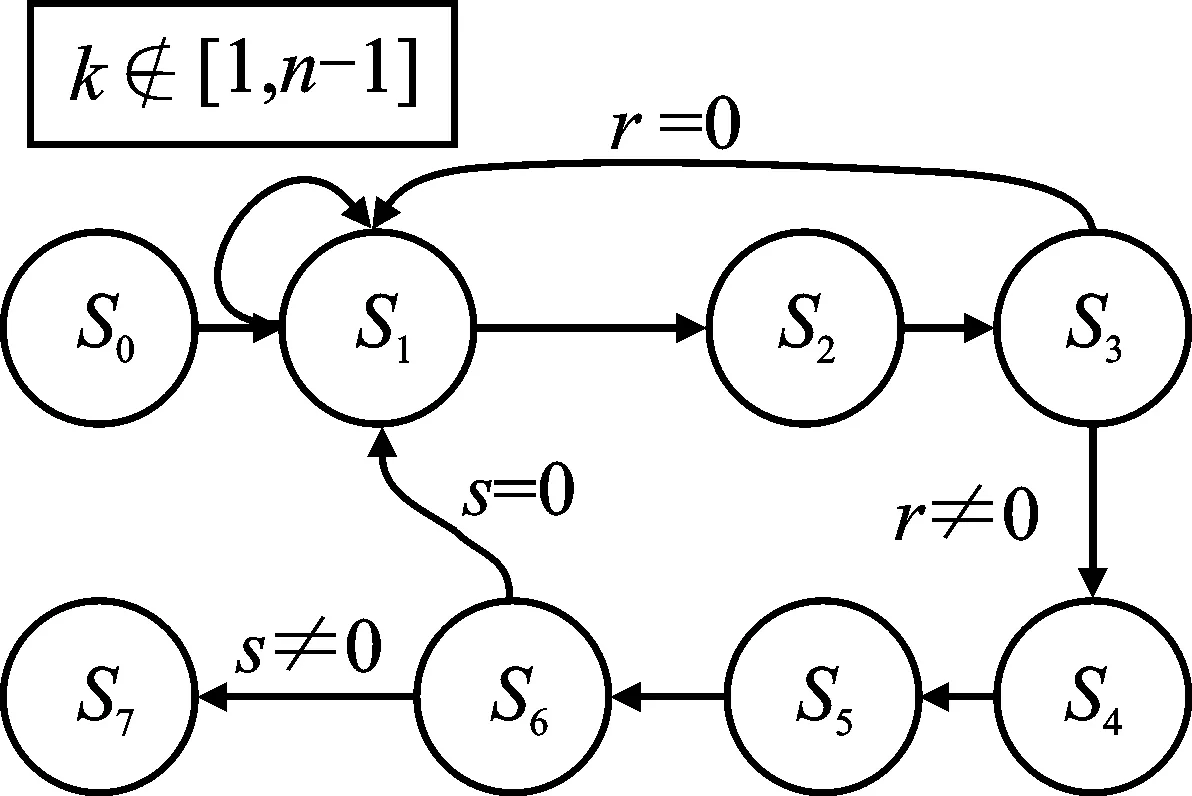
通过上文介绍的双参数数字签名流程,设计有限状态机来调用群运算层和GF(2233)域运算层以此实现数字签名验证系统。签名状态转移如图5(a)所示,具体步骤如下所示:
(a)
(b)图5 状态转移图(a)签名加密 (b)签名验证Figure 5. State transition diagram(a)Signature encryption (b)Signature verification
步骤1S0为初始状态,用户A配置签名参数,包括消息M、椭圆曲线上的一点G,再选择一个私钥d和产生公钥P=dG发送给用户B。
步骤2S1状态随机选取k,若k∈[1,n-1],则进入S2状态计算点乘kG=(x1,y1)。
步骤3S3状态将横坐标x1赋值给签名信息r。若r=0,返回S1状态,反之进入S4状态。
步骤4S4状态计算消息M的离散值e。
步骤5S5状态中随机选取k1、k2。S6状态计算签名信息s=(k2r-er+d)modn,若s≠0,进入S7状态,将签名信息(r,s,k1)传递给B用户。
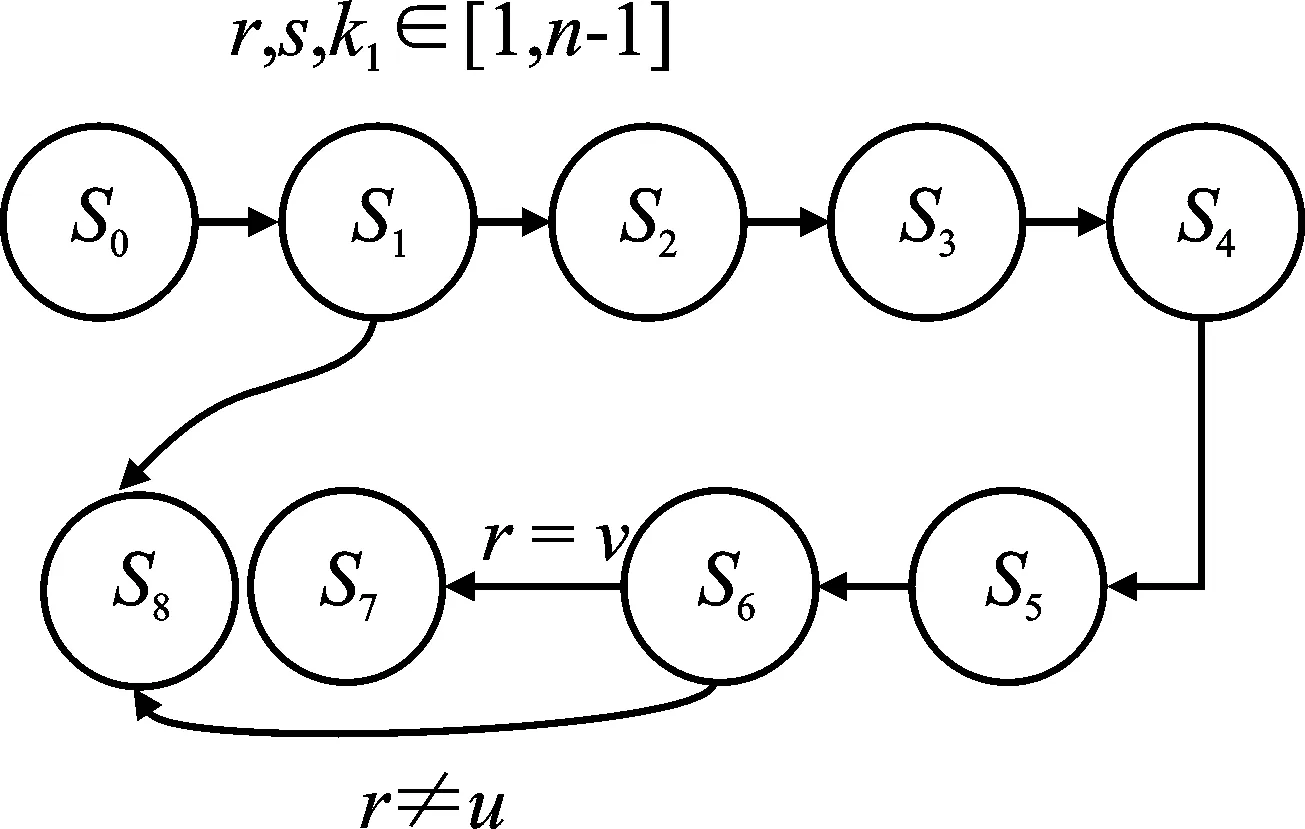
签名验证状态转移如图5(b)所示。用户B对用户A的签名信息(r,s,k1)进行的具体步骤如下所示:
步骤1在S0状态中用户B收到签名信息,进入S1状态验证r,s,k1∈[1,n-1]。若验证失败,则进入S8状态拒绝签名。
步骤2S2状态计算消息M的离散值e;S3状态计算出参数u=(s+k1m+er)。
步骤3S4状态计算点乘uG,S5状态进行点加运算计算uG+Q=(x,y)。
步骤4若S5状态中x≠0,则S6状态将x赋值给参数v。若r=v,进入S7状态签名成功,反之进入S8状态拒绝签名。
3.2 仿真波形分析
图6是通过软件布局布线后生成的ECDSA加密和解密的顶层模块。其中端口M_i、s_o、r_o、k1_o、success_o分别为输入的待处理消息、加密后输出的3种签名信息以及签名验证成功信号。
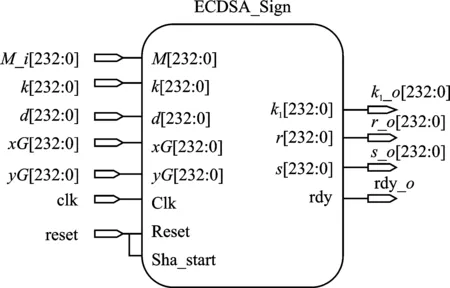
(a)
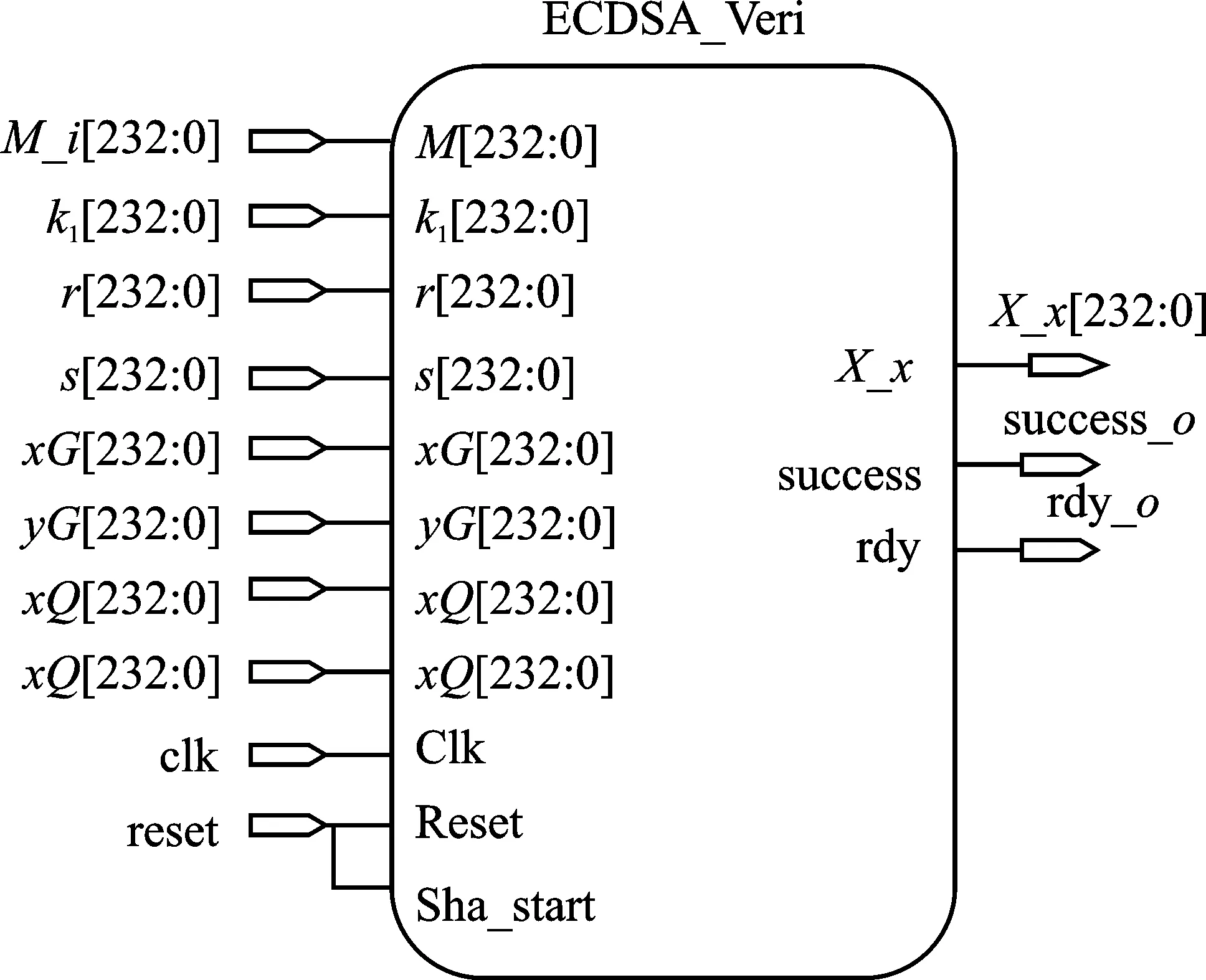
(b)图6 ECDSA加解密顶层模块(a)签名加密 (b)签名验证Figure 6. ECDSA encryption and decryption top-level module(a)Signature encryption (b)Signature verification
本文通过Vivado软件利用Verilog语言对双参数ECDSA架构进行完整的功能仿真,数字签名运算结果如图7所示。待签名消息M=233’h0f1571c947d9e8590cb7add6af7f6798,私钥d=233’h15,随机数k=233’h6a,输出签名消息k1=233’h129、r=233’h0e15ae1d3e035c8d4653ce24cb569e01a62c9cda208cc698c4eb3f3c87a、s=233’h12506c8a4f9be86b284c118269d774e926d19d03ee49250e1f1da7df3db。

图7 数字签名运算的仿真结果Figure 7. Simulation results of digital signature operation
用户A完成数字签名后,将签名信息(r,s,k1)、消息M与公钥Q发送给用户B进行验证签名。签名验证仿真结果如图8所示。输出结果X_x为233’h0e15ae1d3e035c8d4653ce24cb569e01a62c9cda208cc698c4eb3f3c87a。从结果可以看出X_x=r,此时success_o信号出现高电平,表示数字签名方案成功,消息M未受到第三方篡改。

图8 签名验证的仿真结果Figure 8. Simulation results of signature verification
3.3 改进签名算法分析
在本文提出的双参数ECDSA算法中,非法用户窃取到私钥d或者公钥Q其中一个,无法通过Q=dG来求解另一个,此方案具有前向安全性。非法用户将签名消息(r,s,k1)替换为(r′,s,k′1),接收方不能通过签名验证,此方案可以抵御签名消息伪造攻击。无论是伪造私钥d或者伪造消息M来进行数字签名时,得到的都是伪签名信息,签名验证过程无法得到有效的输出,此方案可以保证消息和私钥的完整性和真实性,可以防止数据篡改。非法用户伪造随机数k'发起伪造攻击,进而得到伪造的签名信息,此方案可以抵御替换随机数的伪造攻击。
该方案通过数字签名技术实现了双向认证,非法用户不能冒充任何一方,有效地防止了中间人攻击[15]。接收方基于发送方发送的(r,s,k1)进行验证工作,以保证发送方事后不可抵赖。将改进后的方案与现有的方案进行了安全性对比,3种方案的性能差距如表4所示。

表4 签字方案安全性对比Table 4.Security comparison of signature scheme
本文对基于并行PA和PD运算模块的蒙哥马利点乘法进行仿真实验,表5中列出本文与其他文献方案之间的比较。本文的点乘算法运算过程占用了23 087个逻辑单元,在时钟频率100 MHz下运行4.77 μs完成一次点乘运算。在本文与文献[18]的逻辑单元基本相同的情况下,完成一次点乘运算需要的时钟数减少75%。本文的逻辑单元数略高于文献[17],但完成一次点乘运算时的钟数减少90%。综上,本文提出的点乘运算在面积和速度上均取得较好的折中效果。
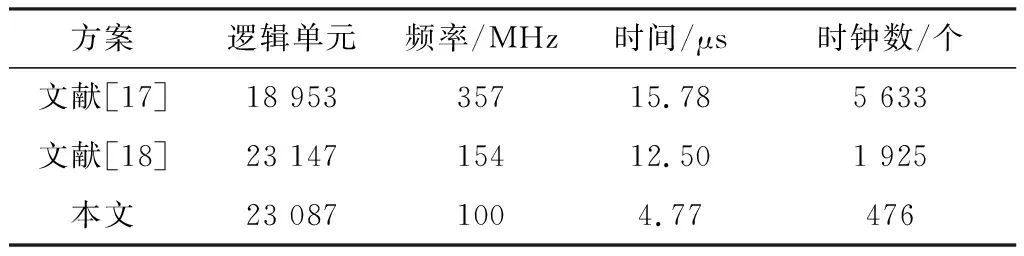
表5 二进制域上PM性能比较Table 5.Performance comparison of PM on binary field
4 结束语
本文针对数字签名的安全性低和运算效率低等问题提出了可证明安全性的双参数ECDSA,并通过GF(2m)上的模运算来实现。本文优化设计串并混合快速模乘运算和Itoh-Tsujii模逆运算,使用并行PA和PD运算提高点乘的运算效率。此外,本文使用LD射影坐标系减少曲线运算中的模逆运算次数。安全性分析结果表明,改进后的签名算法不仅能抵抗伪造攻击,还能有效地抵抗随机数替换。签名算法在Vivado软件上仿真测试结果表明,该算法有效地实现了数字签名验证,确保消息传递过程中的安全性。点乘运算过程占用23 087个逻辑单元,在时钟频率100 MHz下仅需要4.77 μs便完成一次点乘运算。点乘性能对比分析结果表明,利用优化后的模乘、模逆运算和并行运算的思想能提高点乘运算的效率。接下来的研究工作是将ECDSA算法与其他对称加密算法混合使用,实现更加安全有效的密码系统设计。

