基于粒子群优化的TDOA声源定位方法
张大桂,周志峰,张 怡,王立端
(1.上海工程技术大学 机械与汽车工程学院,上海 201620; 2.上海市松江区新桥职业技术学校,上海 201612; 3.上海司南卫星导航技术股份有限公司,上海 201801)
声源定位系统[1-2]常用于设备的故障诊断[3],也可用于新产品的噪声源定位,在语音人机交互中发挥着重要作用。声源定位算法分为最大输出功率波束形成法、高分辨率谱估计法和到达时间差(TDOA)的声源定位方法[4]。前两种方法多用于声源方位角估计,算法复杂度高且计算量大,而TDOA的声源定位算法结构简单且计算速度快,常用于估计声源三维坐标。
TDOA分为时延估计和位置估计两个步骤。第一步时延估计[5]的方法有广义互相关方法[6]、自适应最小均方方法[7]、自适应特征值分解法[8]等。针对广义互相关的时延估计算法,文献[9]提出了一种改进PHAT加权函数的方法,提升了时延估计性能。为了提升时延估计的抗噪能力,文献[10]提出广义互相关的SCOT/PHAT联合加权时延估计算法。TDOA声源定位算法的第二步是位置估计。在对声源位置进行解算的方法如下:在嵌入式的应用中,为了追求计算简单常采用直接计算的方法,但是其抗干扰能力和定位精度都不高。牛顿迭代法[11]也常被用于位置估计,但其定位准确性依赖于初始值,且运算时间长。球形插值法[12]由于计算速度快,定位精度相对较高,得到了广泛应用。但是其抗噪性能较弱,不适用于对定位精度要求较高的场合。文献[12]介绍了基于球形插值法求解声源位置的TDOA方法,并将其应用到了SRP-PHAT(Steered Response Power-Phase Transform)的优化过程中,但并没有针对TDOA算法进行改进。文献[13]在五元三维立体麦克风阵列的基础上设计了一维空间搜索法计算声源的位置,但是此法仅适用于三维立体的阵列。
本文为了解决平面麦克风阵列的声源三维坐标定位问题,在广义互相关算法作为时延估计算法的TDOA声源定位算法中引入粒子群优化算法,将其用于TDOA声源定位的位置估计过程中,从而使TDOA声源定位算法适用于平面麦克风阵列。此外,本文研究发现相较于传统的直接计算法、牛顿迭代法和球形插值法,基于粒子群优化的TDOA声源定位方法具有更好的鲁棒性、定位精度和抗噪性能,能够弥补TDOA声源定位算法在位置解算过程中的不足。
1 时延估计
假设两个麦克风接收到的信号为xi(n)和xj(n)
xi(n)=s(n-τi)+ni(n)
(1)
xj(n)=s(n-τj)+nj(n)
(2)
其中,s(n)为声源信号;ni(n)和nj(n)分别为两个麦克风接收到的噪声;τi和τj分别为两个麦克风相对于参考麦克风接收到的声源时延,所需估计的时延差τij如式(3)所示。
τij=τj-τi
(3)
广义互相关函数法[13]Rgcc(τ)为
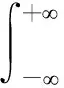
(4)
其中,Gxixj=Xi(ω)Xj*(ω)为互功率谱密度函数;Xi(ω)和Xj(ω)分别为xi(n)和xj(n)傅里叶变换后的结果;Xj*(ω)是Xj(ω)取共轭;ψij为加权函数;e表示欧拉数。当加权函数为PHAT函数时,如式(5)所示时,此加权方式在不改变相位信息的情况下,对功率谱函数进行了白化处理,具有良好的抗噪性能。
(5)
求得Rgcc(τ)的值并对其进行峰值检测,即可得到时延估计结果。广义互相关法求时延估计的原理如图1所示。

图1 广义互相关法原理Figure 1.Principle of generalized cross-correlation method
2 粒子群优化的位置估计算法
假设声源在空间中的位置为Ss=[xs,ys,zs]T,第i个麦克风的位置为mi=[xi,yi,zi]T,则声源到达麦克风j和麦克风i的时间差τij表示为
(6)
式中,c表示声速,一般取340 m·s-1。式(6)中声源位置的坐标是待求解的未知数,至少需要3个方程联列才能求得,以1号麦克风为参考麦克风,选取4个麦克风,列出方程组。由于本文研究平面麦克风阵列,所有麦克风均分布在xoy平面,即zi=0,i=1,2,3,4。为了简化计算,以(x1,y1,z1)作为声源定位系统中三维笛卡尔坐标系的原点,列出如式(7)所示的方程组。
(7)
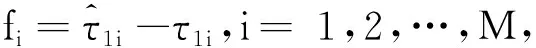
(8)
关于非线性多参数目标函数优化的问题,粒子群优化方法相比于遗传算法速度更快,相比于最速下降法更容易找到全局最优解,因此本文引入粒子群优化算法对声源位置进行搜索。
粒子群优化[14-18]的步骤如下所示:
步骤1初始化粒子的位置和速度,多个粒子组成种群;
步骤2计算所有粒子的适应度值F;
步骤3当F小于粒子的历史最佳位置对应的适应度时,用粒子的位置替换Pbest=(p1,p2,…,pd)中对应粒子的最佳位置,Pbest为所有粒子的历史最佳位置;
步骤4当所有粒子的历史最佳位置计算出的最小目标函数值小于全局的历史最佳目标函数值时,用对应最小目标函数值的粒子位置替换全局历史最优位置Gbest=(g1,g2,…,gd);
步骤5按照式(9)更新粒子的速度,按照式(10)更新粒子的位置
(9)
xi(t+1)=xi(t)+vi(t+1)
(10)
其中,c1和c2分别为粒子学习因子和种群学习因子;r1和r2是两个随机数;t是迭代次数;vi=(vi1,vi2,…,vid)和xi=(xi1,xi2,…,xid)分别表示第i个粒子的速度和位置。在声源定位的位置估计中,粒子的位置即声源的位置,因此空间维数d为3。在式(9)中,惯性权重w的引入使粒子群算法搜索的过程发生了改变。w值越大,则vi(t)值越大,粒子在全局范围内搜索,适用于算法迭代初期,使得粒子能够快速聚集到最优解附近,加快算法的收敛;w值越小,则vi(t)值越小,此时粒子在局部范围内搜索,更擅长在小范围内接近最优解,可提高算法收敛精度,适用于最后接近最优解的迭代。因此,本文选用一种随迭代次数线性减少的惯性权重的设置方式,其计算式为
(11)
式中,wmax和wmin分别为权重最大值和最小值;t和tmax为当前迭代次数和最大迭代次数;
步骤6满足迭代停止条件,输出全局历史最优位置,不满足则返回步骤2。
基于粒子群优化的声源定位流程如图2所示。
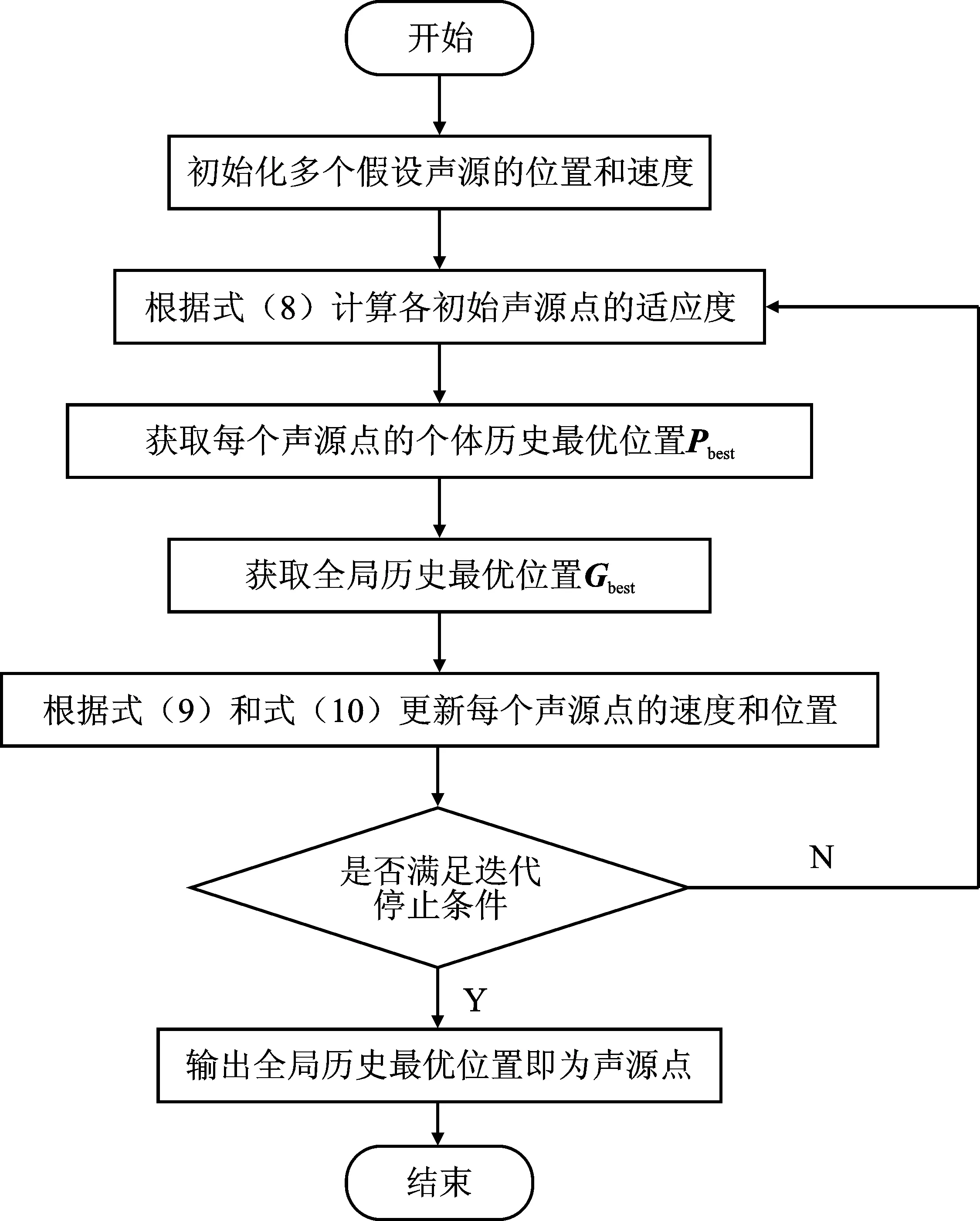
图2 基于粒子群优化的声源定位的流程Figure 2.Flow of sound source localization based on particle swarm optimization
3 算法仿真分析
本文以如图3所示的十六元平面阵列为声源定位仿真的麦克风阵列,以如图4所示的汽车鸣笛的信号为声源信号,对本文提出的基于粒子群空间搜索的声源定位算法进行仿真实验。
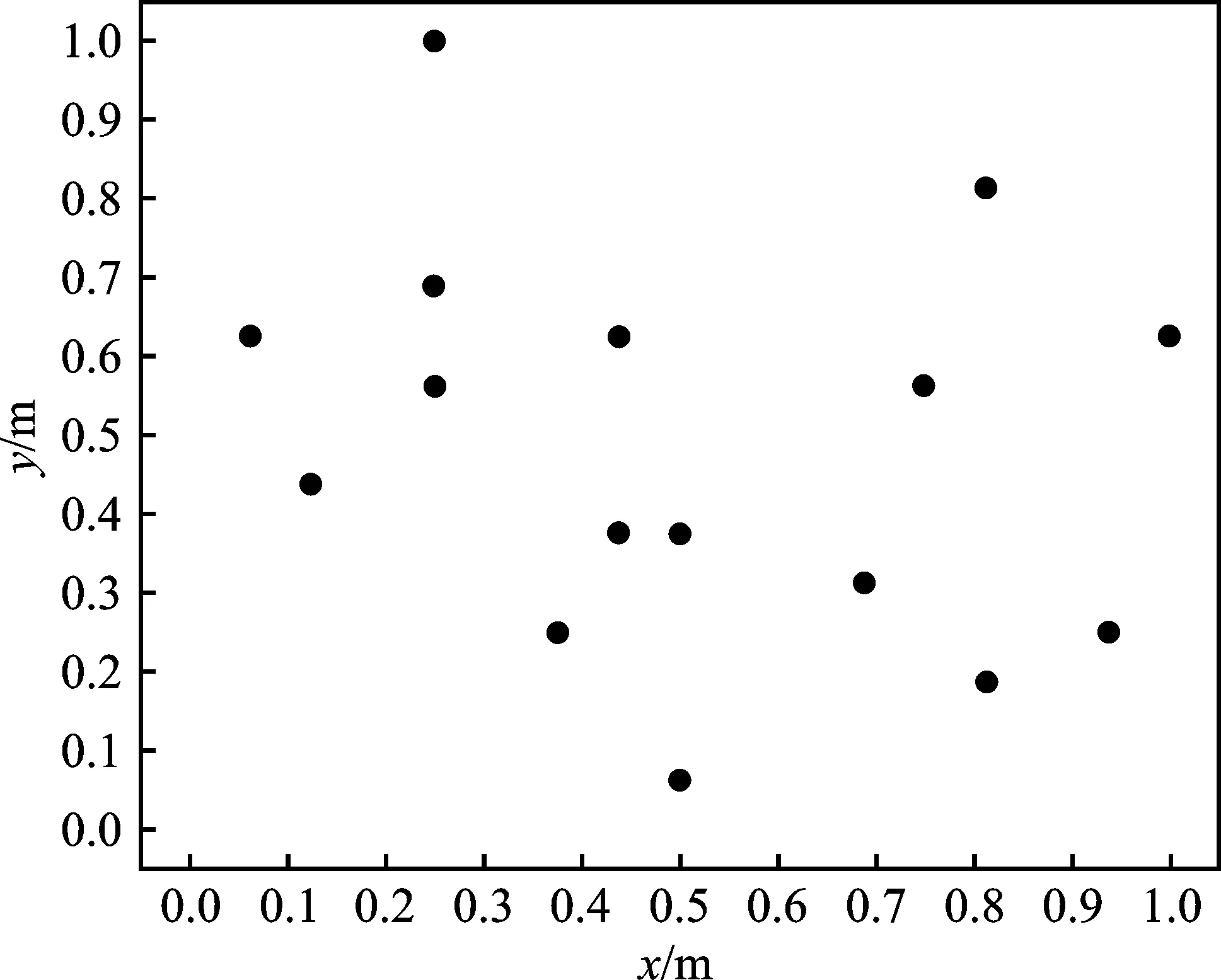
图3 平面麦克风阵列Figure 3. A planar microphone array
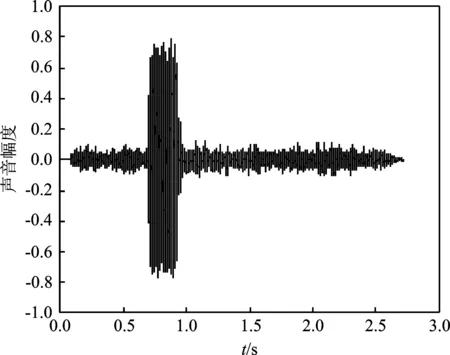
图4 汽车鸣笛声源信号Figure 4. Car whistle sound source signal
3.1 计算效率仿真
在处理器为Intel i7-9750H,内存为32 GB的硬件条件下,分别对直接计算法、牛顿迭代法、粒子群空间搜索法以及球形插值法进行了100次仿真实验,各算法完成位置估计所用的平均时间如表1所示。

表1 各算法计算效率Table 1.Computational efficiency of each algorithm /s
在表1中,牛顿迭代法的迭代停止条件为误差小于10-3时的计算时间。在基于粒子群优化算法的空间搜索法中,将种群数量设置为1 000,迭代次数设为60,c1=c2=0.5,速度限制为[-1,1],惯性权重设为[0.40,0.95]。
由于直接计算法和球形插值法是根据理论推导出的计算式直接进行求解,不涉及迭代过程,所以两者速度最快。由表1可知,虽然引入了迭代过程,但是基于粒子群的空间搜索法与直接计算法、球形插值法计算速度相近。在牛顿迭代法中,初始值的选择影响结果的准确性,误差精度的设置影响迭代次数,对牛顿迭代法的计算速度产生影响,并且牛顿迭代法的计算涉及求导计算。相比于牛顿迭代法,基于粒子群的空间搜索法的迭代次数和种群数量可以根据实际要求进行人为设置。基于粒子群的空间搜索法计算效率相较于牛顿迭代法具有较大提高。
3.2 算法灵敏度分析
在TDOA的声源定位算法中,声源的定位结果受第一步时延估计的影响较大。在实际声源定位中,时延估计会出现偏差,在安装麦克风时也会引入偏差。本文将两者误差统一转换为各麦克风与参考麦克风声程差的误差。
(12)
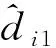
(13)
δ表示所有M-1对麦克风声程差误差的最大误差,即在不同的最大误差δ的情况下,所有麦克风的误差绝对值都要小于等于设定的最大误差δ的绝对值。关于声源定位的位置估算的结果误差定义如下所示。
x轴坐标的误差为
(14)
y轴坐标的误差为
(15)
z轴坐标的误差为
(16)
声源定位结果相对误差为
(17)
随着声程差最大误差δ的不同,声源定位的结果误差也随之发生变化,本文部分实验设置最大误差δ的范围为[-2%,2%]。在此范围内,麦克风与声源的距离偏差都在1 cm以内,以此来验证位置估计算法的灵敏度。
由于直接计算法较为简单,性能较差,牛顿迭代法计算速度慢且依赖于初始值的选取,因此在以下仿真实验中不对这两种方法进行实验对比。球形插值法是基于最小二乘的闭式估计算法,可利用几何关系计算的距离差和时延估计得到的距离差求得矩阵方程的闭式解。其误差方程与式(8)形式类似,且球形插值法在TDOA声源定位方法中应用广泛,因此在下述算法性能分析实验中,将粒子群空间搜索法与球形插值法进行仿真实验对比。
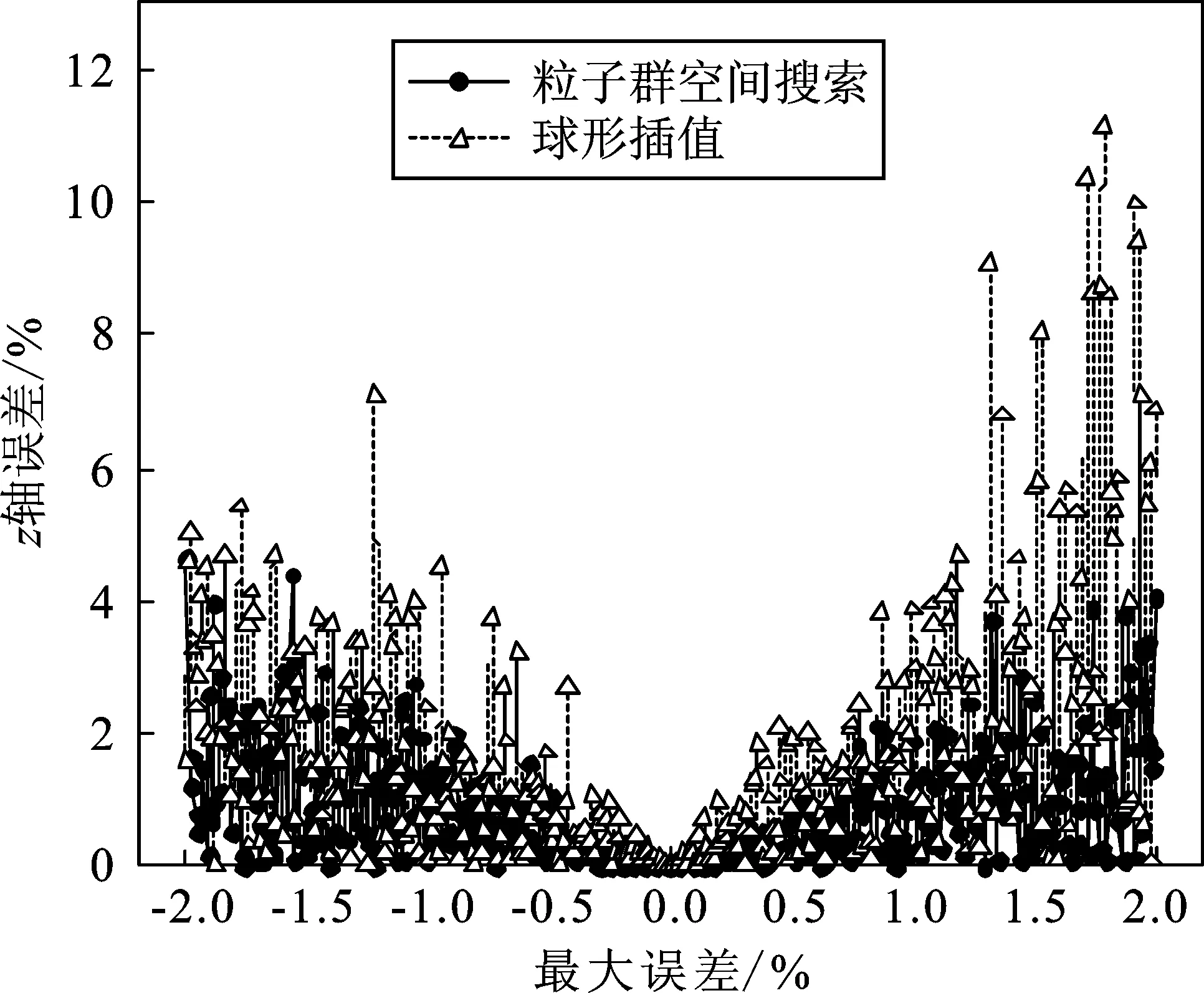
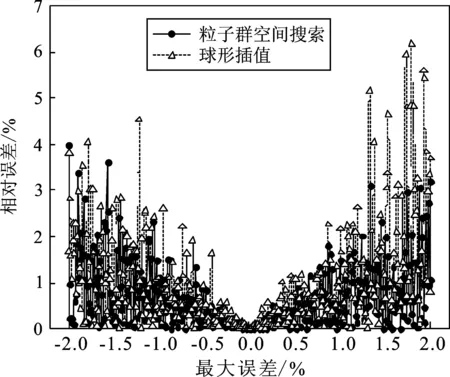
图5是在不同最大误差下,分别利用粒子群空间搜索法与球形插值法对坐标为(6 m, 5 m, 9 m)的声源进行位置估计所得到的位置误差结果比较图。

(a)

(b)
(c)
(d)图5 位置估计误差结果比较(a)x轴误差 (b)y轴误差 (c)z轴误差 (d)相对误差Figure 5. Comparison of position estimation error results(a)x-axis error (b)y-axis error (c)z-axis error (d)Relative error
由图5可知,无论是粒子群空间搜索法还是球形插值法,两者位置估计的误差都随最大误差的增大而增大,其中粒子群空间搜索法在4种误差中普遍小于球形插值法的误差,并且大部分的误差都能保证在3%的误差范围内,只有个别误差会达到4%左右。而球形插值法随着最大误差的增大,其结果误差变化较大,z轴的坐标误差甚至达到了10%左右。
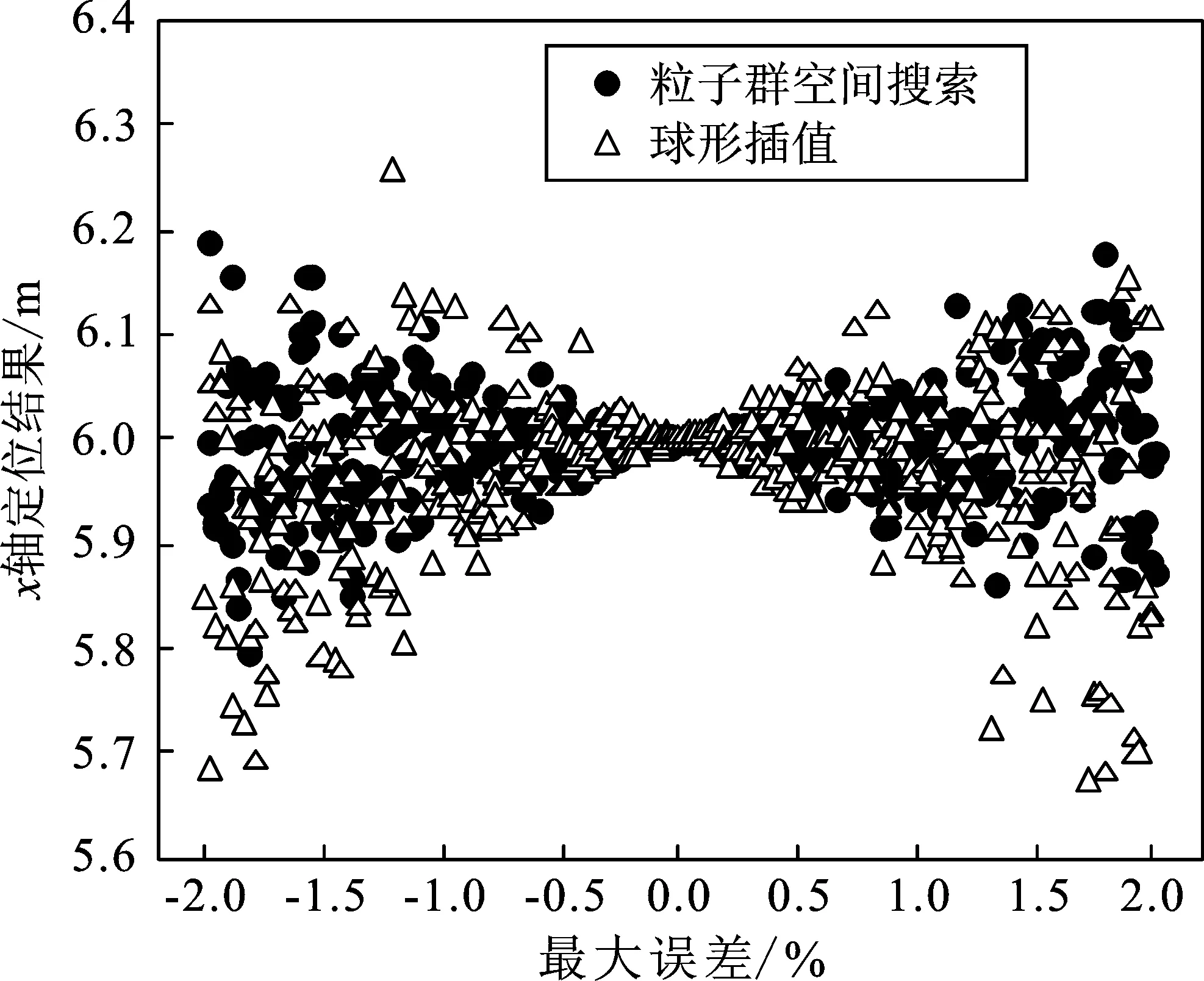
以最大误差为横坐标,以位置估计的结果为纵坐标,得到如图6所示的位置估计结果比较。由图6(a)和图6(b)可知,粒子群空间搜索的x轴和y轴定位结果和真实值的误差在±0.2 m之间,而球形插值法则达到了-0.3 m的误差。由图6(c)可知,两种算法z轴定位结果误差比x轴和y轴坐标的误差更大,大部分误差在±0.4 m的范围内,但是球形插值的结果误差会达到-0.6 m左右。综合上述结果可知,粒子群空间搜索法的定位误差在各方面都要小于球形插值法的定位误差,具有较好的鲁棒性。
(a)

(b)

(c)图6 位置估计结果比较(a)x轴定位结果 (b)y轴定位结果 (c)z轴定位结果Figure 6. Comparison of position estimation results(a)x-axis positioning result (b)y-axis positioning result (c)z-axis positioning result
3.3 不同信噪比下的定位性能
将时延估计的计算结果加入到声源定位的仿真实验中,在不同的信噪比下完成从时延估计到位置估计的整个声源定位算法的仿真。随机生成100个声源位置坐标,其中x的取值范围为[0 m,10 m],y的取值范围为[0 m,10 m],z的取值范围为[2 m, 20 m]。如图4所示的汽车鸣笛信号为仿真信号,在不外加噪声的情况下,粒子群空间搜索法和球形插值法的声源定位误差如图7所示。

(a)

(b)
(c)

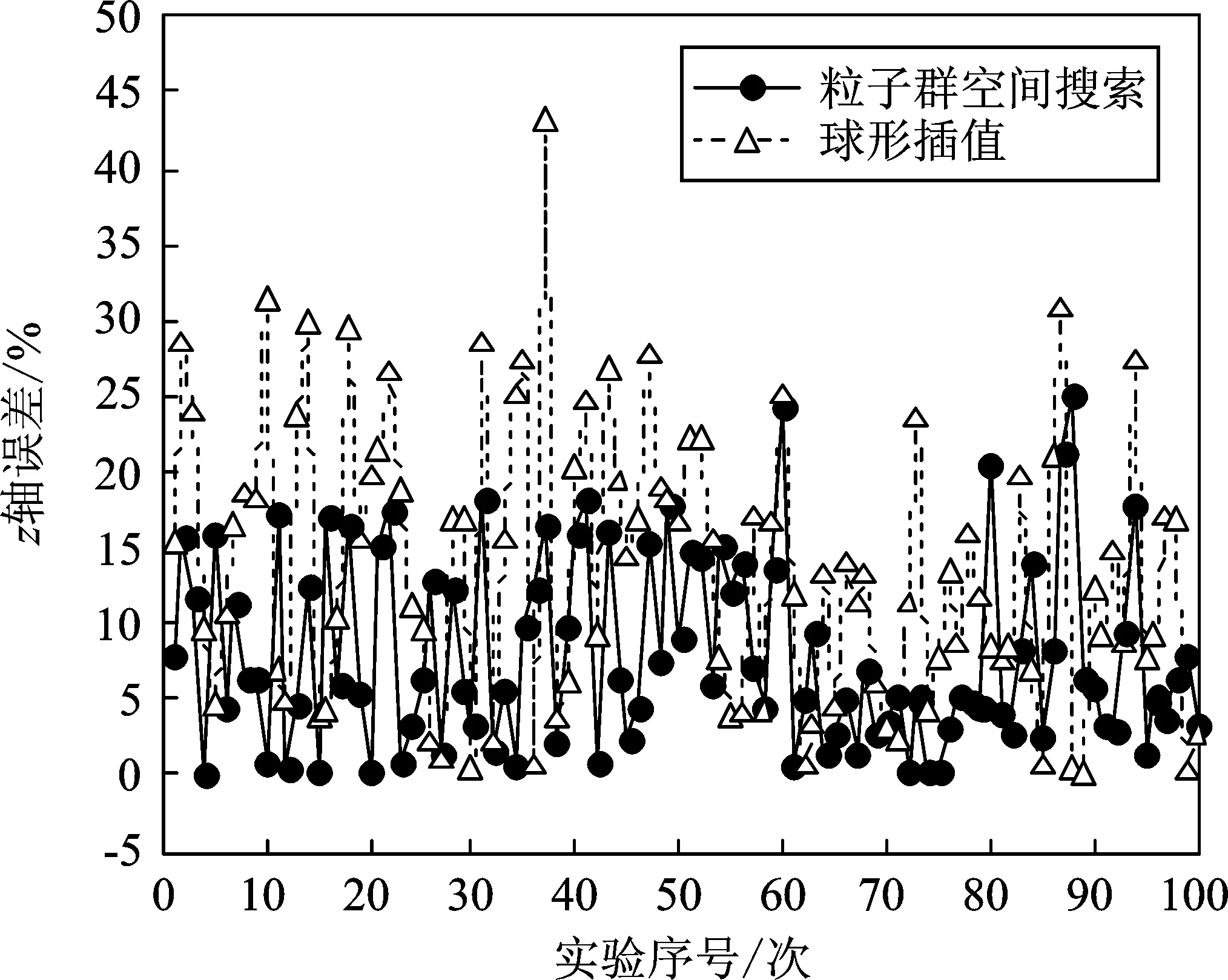
(d)图7 仿真信号位置估计误差结果比较(a)x轴误差 (b)y轴误差 (c)z轴误差 (d)相对误差Figure 7. Comparison of position estimation error results of simulation signal(a)x-axis error (b)y-axis error (c)z-axis error (d) Relative error
由图7可知,粒子群空间搜索法的误差在15%左右及以下,球形插值法的误差大都超过了20%,表明粒子群空间搜索法的定位结果优于球形插值法。将图5中各误差的均值和方差进行统计,结果如表2所示。

表2 无噪声情况下的定位误差Table 2. Positioning error without noise
由表2分析可得,粒子群空间搜索法的每一项误差的均值都要比球形插值的误差均值小5%左右。从方差部分可以看出,粒子群空间搜索法的误差的稳定性也优于球形插值法。在无噪声的情况下,两种方法均出现了一定误差,导致产生误差的因素为时延估计算法在时延估计时的偏差和原始信号夹杂着噪声。当在仿真信号中人为地加入高斯噪声的干扰,设置信噪比为5 dB、0 dB和-5 dB,粒子群空间搜索法和球形插值法的声源定位误差的均值和方差分别为表3~表5所示。

表3 信噪比为5 dB的定位误差Table 3. Positioning error with signal-to-noise ratio of 5 dB

表4 信噪比为0 dB的定位误差Table 4. Positioning error with signal-to-noise ratio of 0 dB

表5 信噪比为-5 dB的定位误差Table 5. Positioning error with signal-to-noise ratio of -5 dB
由表3~表5可知,在信噪比从5 dB降到-5 dB的过程中,粒子群空间搜索法的各项误差均值以大约10%的误差进行扩大,而在此过程中,球形插值法的误差均值随着信噪比的降低而迅速增大。当信噪比为5 dB时,球形插值法的误差均值为40%~50%。当信噪比为0 dB及以下时,球形插值法已经无法有效地实现声源定位。粒子群空间搜索法在-5 dB时的误差均值要优于球形插值法在5 dB时的误差均值,表明粒子群空间搜索法在不同信噪比下的定位性能都要优于球形插值法。
4 结束语
本文将粒子群优化算法应用于TDOA声源定位算法的位置估计中,提出了以时延真实值和估计值差值的平方和为适应度函数的粒子群算法的空间搜索法。
在计算效率方面,本文通过仿真对比了直接计算法、牛顿迭代法以及球形插值法,并在灵敏度和不同信噪比下的声源定位性能这两个方面对比了基于粒子群算法的空间搜索法和球形插值法。仿真结果表明,粒子群空间搜索法和球形插值法在计算速度上相近,且粒子群空间搜索法在鲁棒性、准确性和抗噪性能方面均优于球形插值法。

