基于块效应谱分析的JPEG图像旋转角度估计
党良慧,张玉金
(上海工程技术大学 电子电气工程学院,上海 201620)
图像数字化的过程主要分为3个步骤[1]:采样、量化和编码。目前JPEG(Joint Photographic Experts Group)格式是互联网上较常见的图像格式,也是获取信息的主要来源之一。图像编辑工具的普及使得JPEG图像易被篡改,因此JPEG图像的取证研究具有重要的理论意义和现实意义。与传统主动取证相比,被动取证不需要更多额外信息(水印或签名),因此其具有更广泛的应用前景[2]。在图像拼接篡改中,对局部拼接区域进行重采样处理(例如旋转、缩放等)可以使伪造图像在几何视角上更加逼真[3]。因此,检测局部图像区域经过重采样处理有助于定位篡改区域,本文主要针对JPEG图像的旋转角度估计展开进一步研究。
文献[4]提出期望最大化(Expectation Maximization,EM)算法进行检测重采样,该方法不仅耗时且对初始值较为敏感。文献[5]采用了一个线性预测器,并提出了一种基于p-map的自动检测器,降低了算法的计算复杂度。文献[6]应用二维差分信号的Radon变换来估计旋转角度。文献[7]采用二阶循环平稳法检测重采样引起的周期性。在此基础上,文献[8~9]进一步对两次复合重采样处理进行了理论分析,提出了一种面向图像复合重采样的取证方法。文献[10]利用旋转图像中每一行的相位差来鉴定旋转和缩放因子。文献[11]研究了频域图像二阶导数中不同尺寸窗口内的归一化能量密度,并利用该特征推导出一个19维的特征向量,利用SVM(Support Vector Machine)分类器进行训练以鉴定重采样因子。文献[12]采用一维信号的最大似然估计和分段线性插值来估计重采样因子,通过计算给定图像块的奇异值分解(Singular Value Decomposition,SVD)和测量图像块的每行/列的饱和像素[13]区分原始图像和重采样图像,并在文献[14]中对该方法进行了的改进。
当待测图像未经过JPEG压缩或者压缩率较低时,上述图像重采样检测方法能够取得较好的性能,然而这些方法易受JPEG块效应影响。针对JPEG图像重采样因子估计问题,文献[15]引入秩统计理论并结合光谱分析法进行JPEG图像下采样因子的估计。文献[16]在文献[8~9]的基础上利用循环谱分析来估计JPEG图像旋转角度。上述JPEG图像重采样取证方法适用于图像块尺寸较大、旋转角度较大的情形。当JPEG图像被重采样后,其块效应网格会产生一定程度的偏移。文献[17]提取JPEG图像的块效应网格并将其转换到傅里叶变换域,通过分析傅里叶谱的峰值特性以鉴定JPEG图像是否经历重采样处理。然而,复杂的图像纹理会对提取块效应网格产生一定的干扰,该方法的检测精度还有提升空间。本文引入变异蚁群算法将图像的像素强度值转化为人工蚂蚁在图像中留下的信息素值,根据累积的信息素提取图像的边缘得到二值图像[18]。参考二值图像中边缘的位置,将JPEG图像中属于边缘位置的内容移除。以上步骤可削弱图像内容的影响,提取受纹理干扰较小的块效应网格,进而利用傅里叶谱分析进行JPEG图像旋转角度的估计。
1 移位的块效应网格特征
对一幅图像进行JPEG压缩的基本流程主要包括彩色空间转换、8×8分块离散余弦变换、量化、Huffman编码等步骤,解压缩是上述压缩步骤的逆过程。由于每个图像块都被单独量化,块内部区域较平滑,而块与块之间的过渡较为剧烈。这种现象在整个图像的水平和垂直方向上周期性地出现,形成块效应网格(Block Artifact Grid,BAG)。压缩率越高,图像的质量越低,BAG也会越明显。通过分析BAG的周期性特性可以为区分JPEG单压缩和双压缩提供有效依据,进而定位JPEG图像拼接篡改区域[19]。
给定一幅大小为M×N的JPEG压缩图像,BAG以水平线和垂直线组成,当JPEG图像经过旋转之后,BAG也以同样的角度发生了旋转[17],该过程如式(1)所示
(1)
式中,T为块效应网格的周期;δ(·)为Dirac-Delta函数。原始JPEG图像块效应网格的周期性为8,图像旋转会对BAG的周期性产生相应的影响,导致其变为移位的块效应网格(Shifted Block Artifact Grid,SBAG)。为了分析BAG的周期性,本文使用傅里叶变换将其变换到频域,如式(2)所示。
(2)
由式(2)可以看出,只有当u或者v是M/T或者N/T的整数倍时,F(u,v)是非零值,非零值的位置呈现峰值状态。因此,第一象限(kM/T,lN/T)在网格上有T2个峰[17],对应的幅值分量如式(3)所示
(3)
式中,n1和n2是整数,并且n1,n2∈[1,T]。频谱中峰的类型可以分为原点峰、坐标轴峰和网格峰3类。相应的峰值分别用|F(O)|、|F(A)|和|F(G)|表示。根据式(3)计算可得式(4),如下所示。
(4)
未经历重采样的JPEG图像由于压缩会产生周期为8的块效应,当其经历重采样(旋转、缩放)后,导致原本周期为8×8的网格改变大小。当网格缩小为一个像素时将导致块效应完全消失,因此本文选取T>2来避免这种情况的发生。再结合式(4),可以进一步得到3类峰值对应的关系,如式(5)所示。
|F(G)|<|F(A)|<|F(O)|,|F(G)|<0.3|F(O)|
(5)
由式(5)可知,网格峰的幅值小于原点峰和坐标轴峰的幅值。因此,可以通过设定阈值去除网格峰的干扰,进而通过高斯高通滤波移除原点峰的干扰,最后保留坐标轴峰。当JPEG图像被旋转一定角度后,块效应网格发生了相应的偏移,坐标轴峰也会被旋转相应的角度。图1为JPEG图像及其旋转前后的坐标轴峰变化。
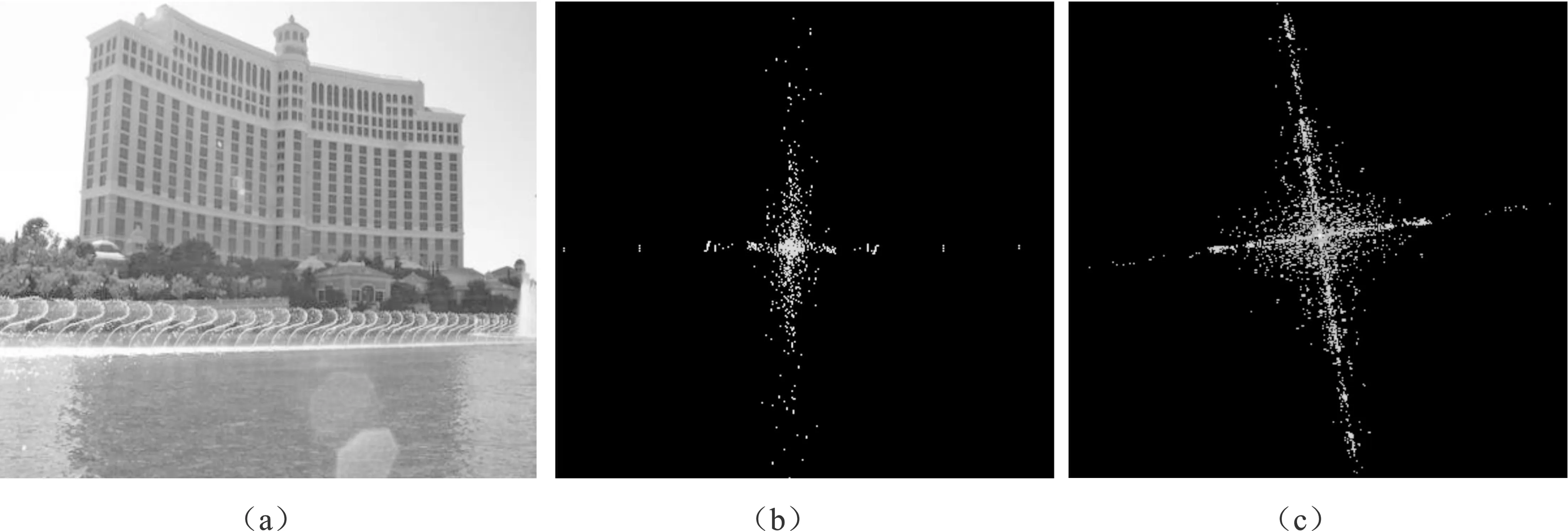
图1 JPEG图像及其旋转前后的坐标轴峰变化(a)质量因子为60的JPEG图像 (b)未旋转的JPEG图像块状效应网格的频谱图(c)旋转10°之后块效应网格的频谱图Figure 1. JPEG image and the variation of its axis peaks before and after rotation(a)JPEG image with a quality factor of 60 (b)Spectrogram of block artifact grid of the unrotated JPEG image (c)Spectrogram of the block artifact grid after rotating by 10°
2 本文算法
由前文可知,JPEG图像旋转操作会产生移位的块效应网格(Shifted Block Artifact Grid,SBAG),然而SBAG的提取易受图像内容干扰,这种干扰在图像块尺寸较小、旋转角度较小时尤为明显。因此,本文引入基于变异蚁群的图像边缘检测算法,以此减小图像内容的影响。在此基础上,提取块效应网格,通过傅里叶变换进行频谱分析,估计JPEG图像的旋转角度。图2为本文算法的主要流程,具体的算法步骤如下所示:
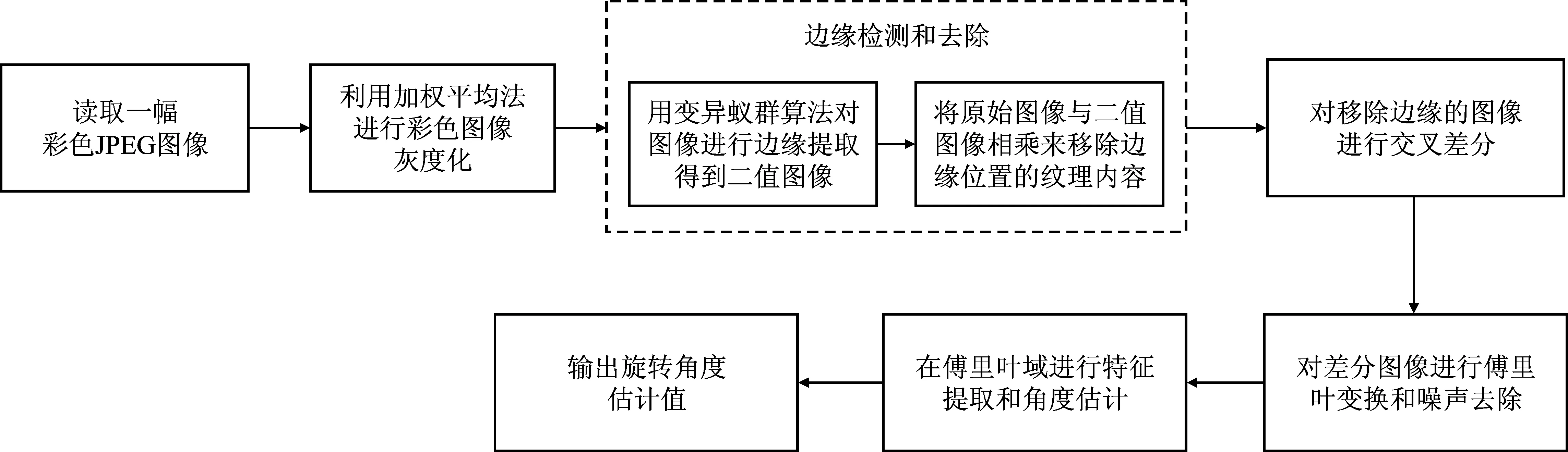
图2 旋转角度估计算法流程Figure 2. Flow of rotation angle estimation algorithm
步骤1读取一幅彩色JPEG图像;
步骤2采用加权平均法对旋转后的彩色图像进行灰度化处理得到图像I,I=0.299R+0.587G+0.114B;
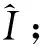
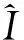
步骤5对步骤4得到的差分图像进行傅里叶变换和噪声去除处理;
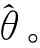
2.1 边缘检测与去除
图像边缘是像素强度变化剧烈的区域集合,对应图像中物体的轮廓特征。图像边缘检测旨在提取图像中物体呈现的边缘,对于理解图像的内容较为重要[20]。图像中与内容相关的边缘对JPEG图像块效应网格提取会产生干扰。传统的边缘检测是基于数字微分方法例如Sobel、Roberts、Laplacian算子等,容易导致破碎的边缘伪影,干扰边缘检测与移除的准确性。针对此问题,本文引入变异蚁群算法[18],利用优化后的智能蚁群系统构建图像的感知图,可以更完整地提取图像的边缘特征,削弱边缘伪影的影响,之后将其移除以突显块效应网格。
基于变异蚁群算法边缘检测的主要思想是:蚂蚁在图像上根据像素值变化的大小构建信息素矩阵,以信息素值表示图像强度值,从而对图像进行边缘检测和提取。其中,蚂蚁的运动方向根据输入灰度图像中的像素值差异的强弱来确定,蚂蚁更倾向于向像素值差异变化较强的方向移动。蚂蚁在变化较强的地方留下的信息素会越来越多,从而形成一个正反馈。给定大小为M×N的图像I,像素点为蚂蚁进行选择的路径节点,边缘为蚂蚁要选取的路径。蚂蚁从某个像素点出发,可以在该像素点的邻域节点活动,并根据节点信息素强度和启发式函数计算转移概率,同时会在经过的节点上释放信息素。经过多次迭代后,信息素较高的区域为图像边缘。具体步骤如下所示:
步骤1初始化过程。将L只人工蚂蚁随机放置在图像的像素点上,将每个像素点的初始信息素值即τinit设置为0.000 1。
步骤2节点过渡规则构建过程。在第h次迭代过程中,蚂蚁在像素点(r,s)选择其邻域任意一个像素点即(x,y)的概率如式(6)所示。
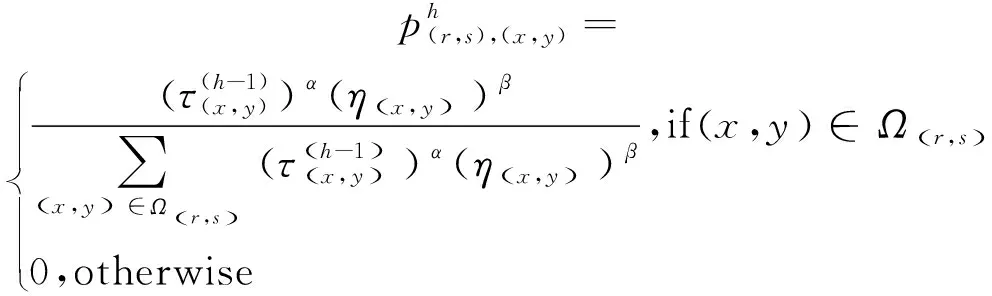
(6)
其中,τ(x,y)和η(x,y)分别表示蚂蚁在像素点(x,y)信息素强度值和启发式信息值;α和β分别表示信息素浓度和启发式信息在计算概率时的影响权重。若α=0,说明启发信息在概率计算中占据主导地位;若β=0,说明信息素浓度在概率计算中占据主导地位。
如图3所示,该方法采用8连通性邻域来确定蚂蚁在节点(r,s)上允许移动的范围,用集合Ω(r,s)表示,被选中的节点为(x,y)∈Ω(r,s)。为了提高蚂蚁感知节点的能力,本文将启发式函数定义为式(7)
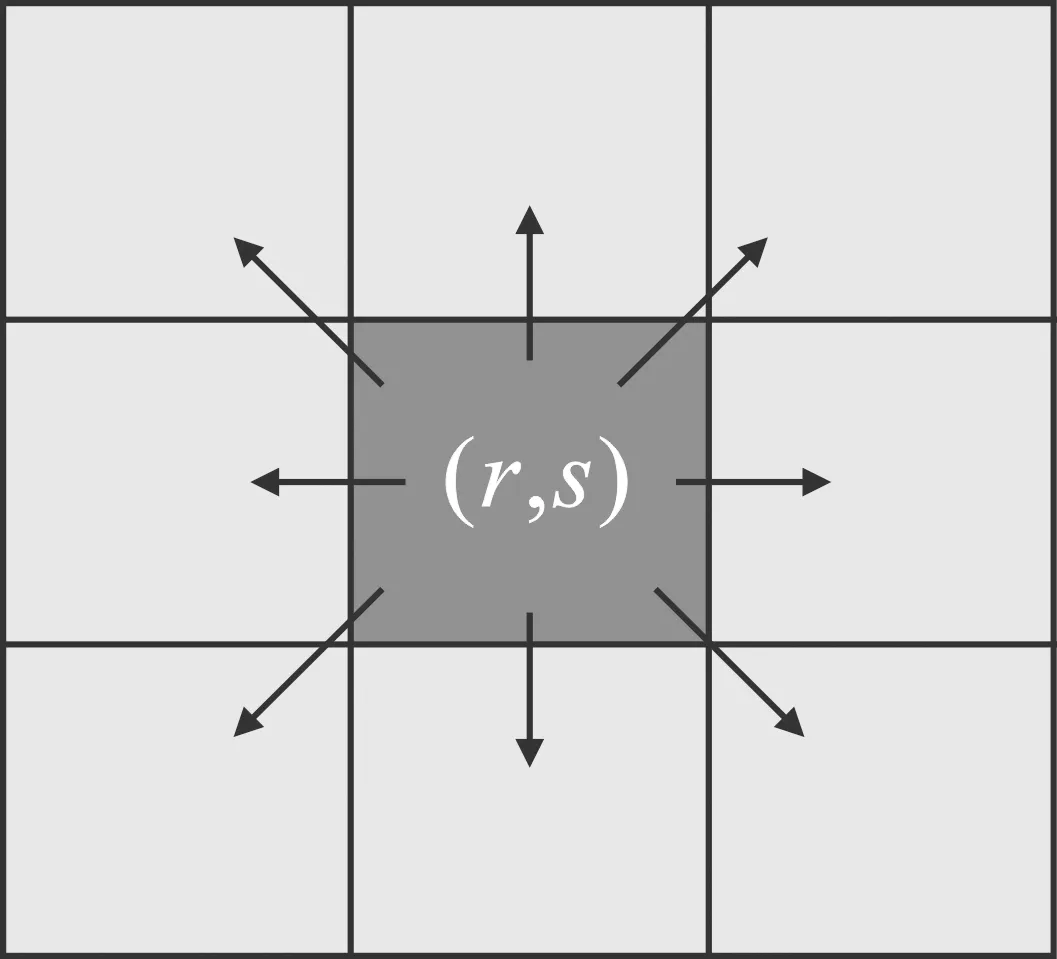
图3 蚂蚁在节点(r,s)移动的邻域范围Figure 3. Admissible range of the ant movement at node (r,s)
(7)
其中,u∈{0,1,2},v∈{-2,-1,0,1,2};Imax为图像I的最大强度值;I(x,y)为节点(x,y)处的强度值;max(·)是两个节点强度差的绝对值最大值。
步骤3信息素更新规则。在每一个构造过程中,L只人工蚂蚁移动完后,信息素值按照如式(8)所示的规则更新
(8)
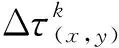
(9)
其中,k(x,y)=1表示第k只蚂蚁访问了节点(x,y);T为自适应阈值,用于控制信息素更新过程中信息素的沉积,该参数只允许蚂蚁在沿启发式信息值T以上的边缘移动时存储信息素。
步骤4终止准则。达到最大迭代次数后,算法终止。
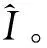

表1 相关参数设置Table 1. Related parameters setting
2.2 无关峰值移除和角度估计
通过基于变异蚁群算法的边缘检测和移除、交叉差分处理,图像纹理的干扰被有效地减弱。由于JPEG图像块效应网格具有周期性,对其进行傅里叶变换可以在频域上展现出明显的峰值,因此可以对块效应网格进行傅里叶变换转换到频域,通过检测频谱的峰值从而实现特征提取和角度估计。操作过程如图4所示,具体操作步骤如下所示:
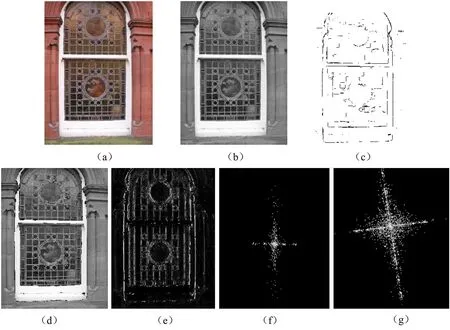
图4 图像旋转前后的块效应谱分析实例(a)JPEG原图(b)灰度图(c)边缘图(d)边缘削弱图(e)差分图(f)未篡改图像频谱图(g)旋转9°之后的频谱图Figure 4. An example of block artifact spectrum analysis before and after image rotation(a)JPEG image (b)The corresponding grayscale image (c)The edge image (d)The edge reduction image (e)The difference image (f)Spectrum of an untampered image (g)Spectrum after 9° rotation
步骤1将经过处理后得到的差分图采用零值填充,进而得到一个大小为M×N的方阵,其中N是2的整数次幂。
步骤2使用快速傅里叶变换将方阵转换到频域,然后将零频分量转移到中心位置,之后在频谱图上沿着网格(kM/T,lN/T)(大小为M×N的图像)可以观察到如式(3)所示的较为明显的峰值。
步骤3移除无关峰值,以减少干扰。网格峰的峰值比较微弱,容易被破坏。为了减少网格峰的干扰,本文应用阈值τ|F(0)|从频谱图中去除网格峰,其中τ是一个实数,取值区间为0.3<τ<1。实验结果表明,当τ=0.7时,能更好地移除网格峰。
针对去除网格峰后的频谱图,应用高斯高通滤波器去除原点峰和一些低频分量。其中高斯高通滤波器(Gaussian High-Pass Filter,GHPF)的计算式如式(10)所示
(10)
其中,D0表示通带半径;e为欧拉数;D(u,v)是到频谱中心(M/2,N/2)的距离(u,v)(欧氏距离),如式(11)所示。
D(u,v)=[(u-M/2)2+(v-N/2)2]1/2
(11)
步骤4坐标变换。经过以上步骤,频谱图中只保留了坐标轴峰,再对频谱图的尺寸进行归一化后,未经历重采样的图像其坐标轴上的峰位于频谱图的1/8、1/4、3/8、1/2位置(以原点为参考点)。当JPEG图像经历旋转操作后,坐标轴峰在频率域也会旋转到相应的角度,峰与原点的距离仍然保持不变[17]。
步骤5角度估计。为了提取JPEG图像经过旋转后所留下的特征,本文通过坐标变换的方式对傅里叶变换前后的f(x,y)和F(u,v)进行极坐标变换,得到f(r,θ)和F(ω,φ),然后就有f(r,θ+θ0)⟺F(ω,φ+φ0),即空间域图像旋转角度与频域图像旋转角度相同。本文将频谱图转换到极坐标中,其中极角坐标的取值区间为[0,2π],极径坐标的取值区间为[0,N/2]。JPEG图像的旋转角度对应于极坐标中的峰值位置,通过提取极坐标中峰值的位置得出角坐标的大小从而得到旋转角度的估计值。由于傅里叶域的对称性,本文仅在第一象限提取峰值。
3 实验结果与分析
为了定量评价本文所提方法的性能,从Dresden image database[21]获取200张未经压缩的彩色图像。为了避免相机内部可能产生的CFA插值的干扰,本文使用最近邻核函数将每张图像下采样两倍[22-23]。现有基于光谱分析的JPEG图像旋转角度估计算法大多受到图像块像素大小和旋转角度强弱的影响,对于旋转角度位于[1°,15°]内的64×64尺寸的图像块,算法检测误差较大。为了验证本文方法对小尺寸图像块和旋转角度较小时的检测性能,以当前较难检测的双三次核插值对图像旋转进行实验,首先用给定的5种压缩质量因子{50, 60, 70, 80, 90}对选取出的未压缩图像进行JPEG压缩,然后从这些压缩图像中选取64×64的中心区域,以1°为步长、[1°,15°]为区间的旋转角度生成待测图像进行评估。
本文采用平均绝对误差[16]作为JPEG图像旋转角度估计的性能评价标准,平均绝对误差定义如式(12)所示
(12)
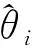
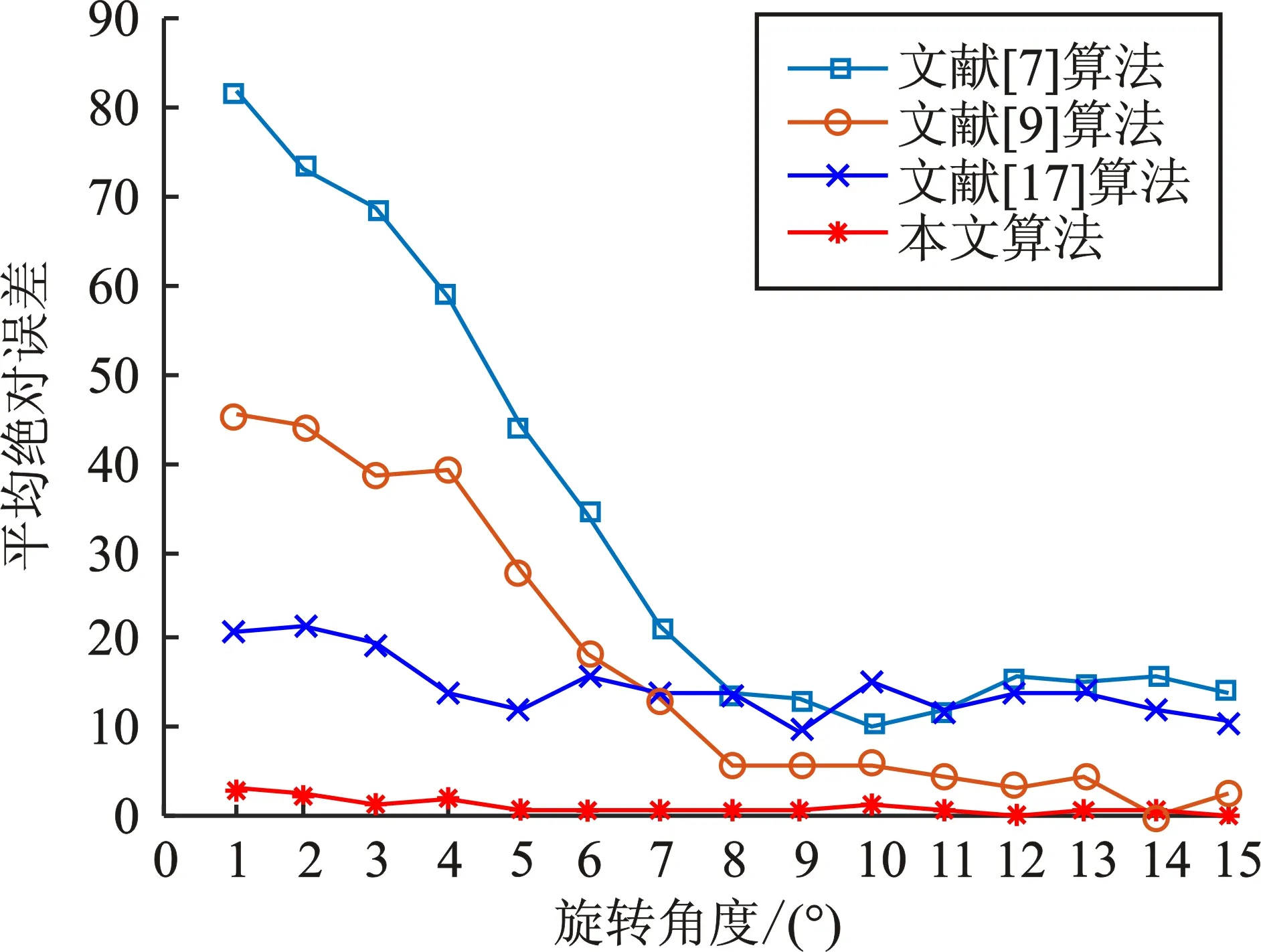
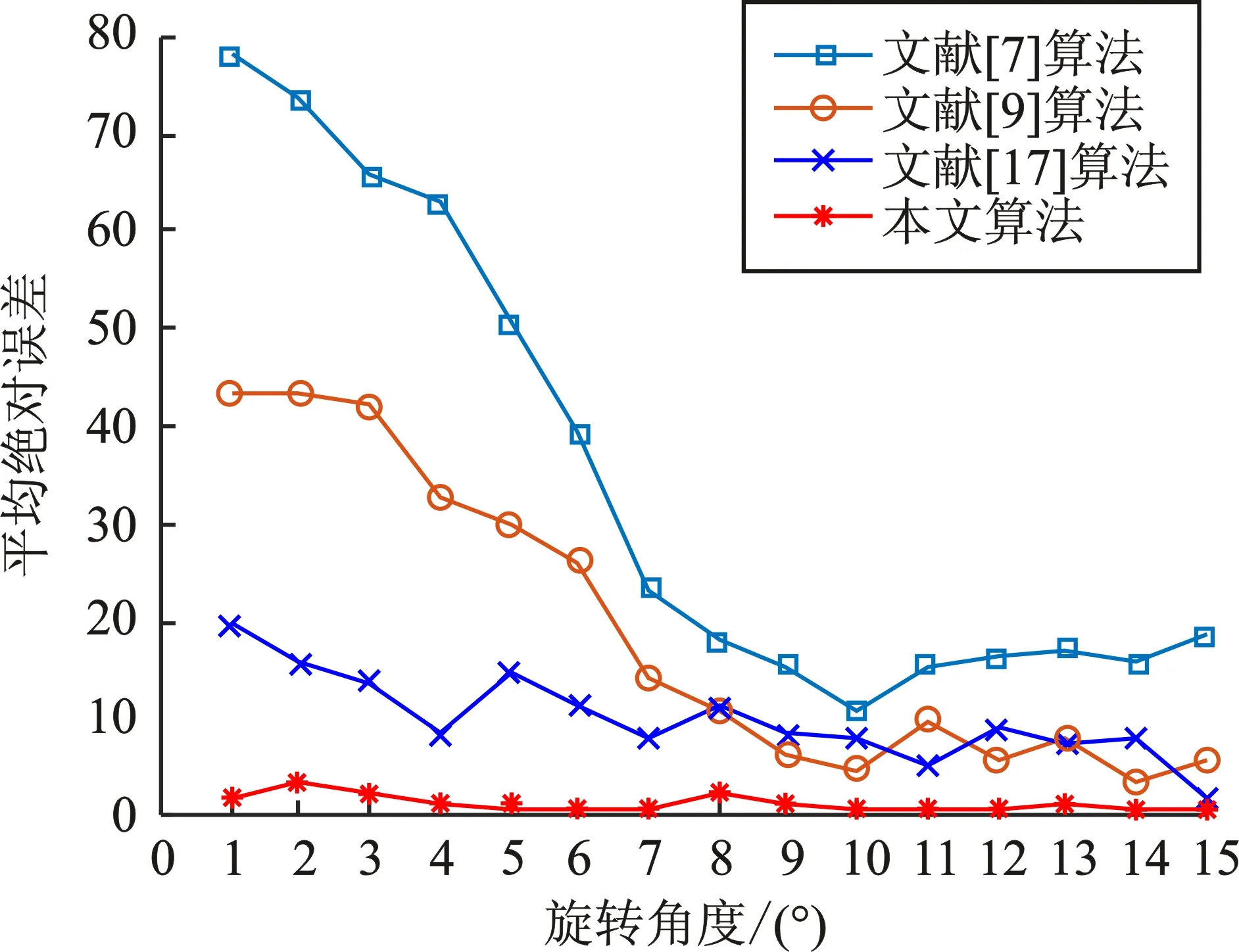
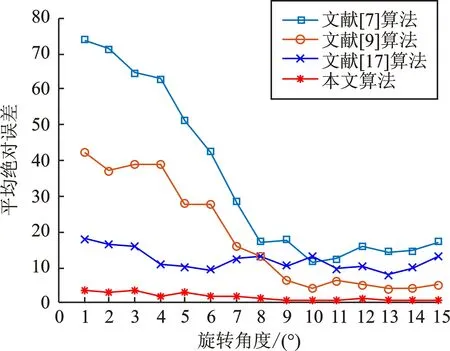
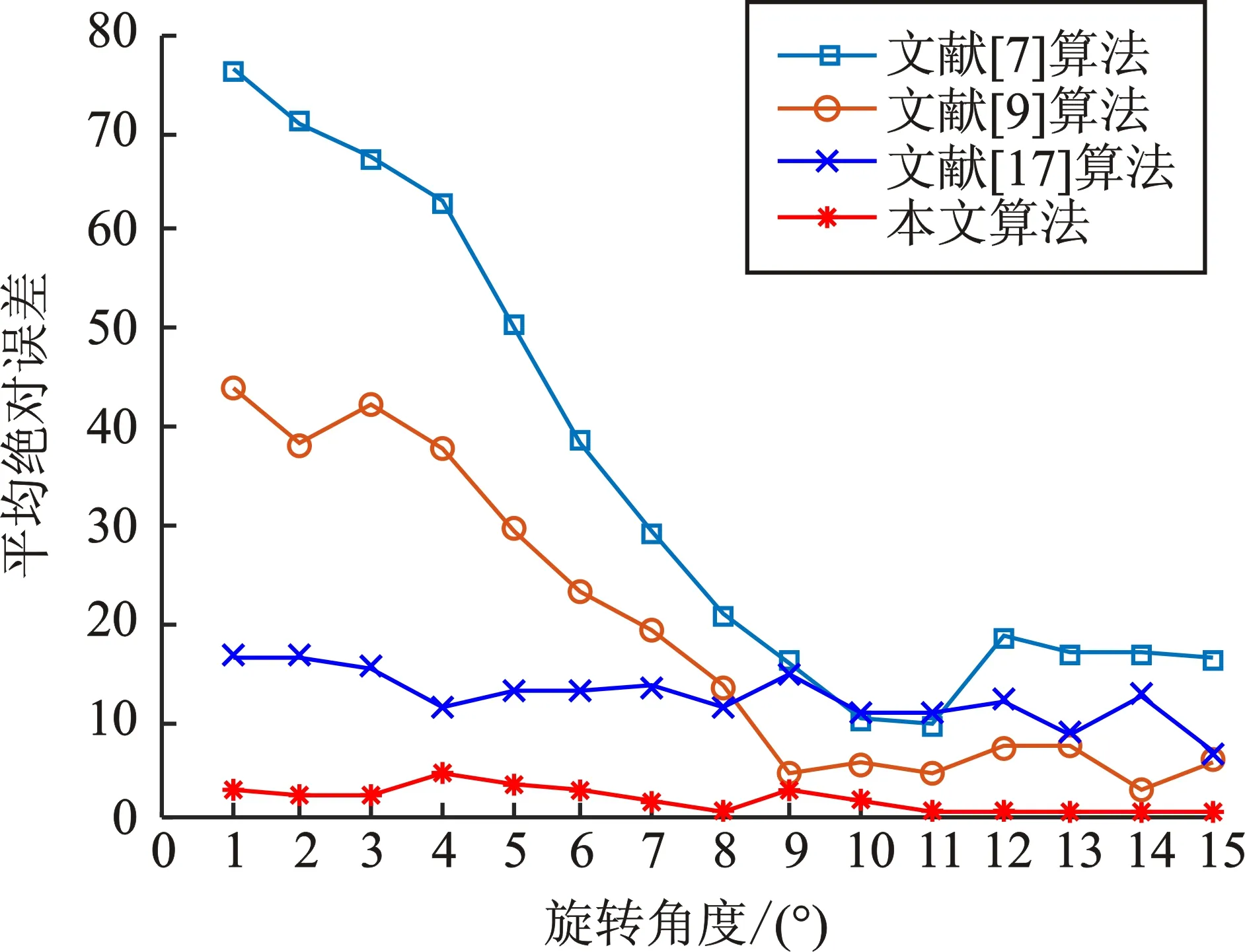
图5显示的是不同质量因子(Quality Factor,QF)下的JPEG图像旋转角度估计性能对比。当旋转角度为1°~8°和9°~15°时,本文方法与现有方法在不同质量因子下的平均绝对误差对比结果如表2和表3所示。其中,最小的检测误差以粗体表示。通过对图5、表2和表3进一步分析,可以得到如下结论:
(a)
(b)
(c)
(d)
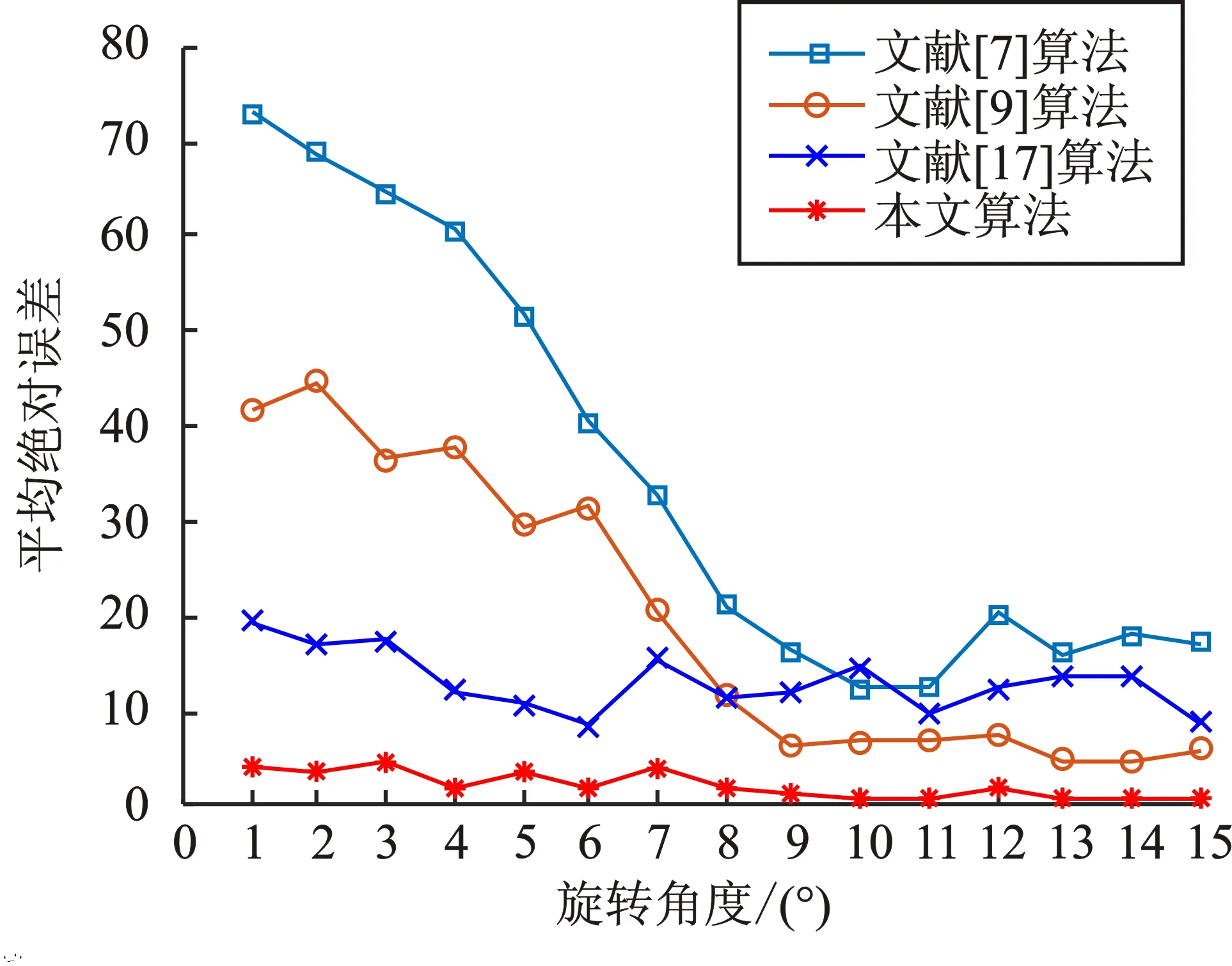
(e)图5 不同质量因子下的JPEG图像旋转角度估计性能对比(a)QF=50 (b)QF=60 (c)QF=70 (d)QF=80 (e)QF=90Figure 5. Comparison of JPEG image rotation angle estimation performance with different quality factors(a)QF=50 (b)QF=60 (c)QF=70 (d)QF=80 (e)QF=90
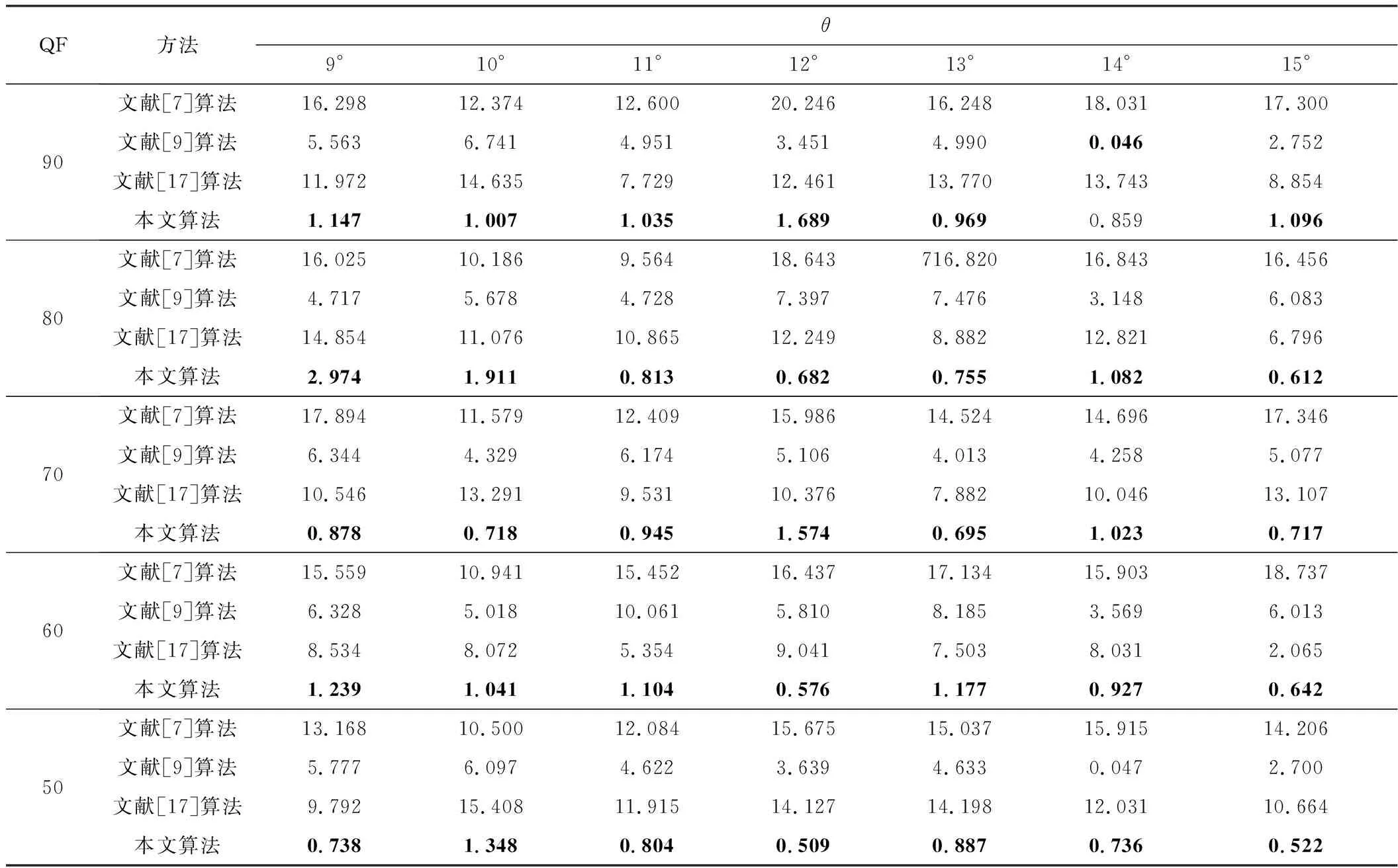
表3 旋转角度在9°~15°时,不同质量因子下4种算法的平均检测误差Table 3. Average detection error of the four algorithms for different quality factors at rotation angles of 9°~15°
1)当旋转角度在1°~8°时,本文方法比现有方法的平均检测误差低且鲁棒性更好。其主要原因是本文采用的变异蚁群边缘检测与去除算法能够更完整地提取块效应网格进行谱分析,有效解决了旋转角度较弱时重采样峰难以被检测及旋转角度估计不准确的问题。
2)当旋转角度在9°~15°时,现有方法的平均检测误差逐渐减小并趋于平稳。这是因为虽然随着旋转角度增大,文献[7]和文献[9]方法的重采样周期性较容易被检测,但本文方法和文献[17]方法的性能仍然要优于上述两种方法。
3)针对旋转角度位于[1°,15°]区间内的小尺寸图像,对于不同压缩质量因子,本文方法均能够有效消除图像纹理对块效应网格的干扰,从而较准确地提取坐标轴峰进行旋转角度估计,比现有方法具有更好的鲁棒性。
4)当旋转角度不变时,质量因子越小,其检测性能越好。主要原因在于:JPEG图像质量因子越小,图像压缩率越高,图像块效应网格更容易被提取进行频谱分析,进而可以更准确地进行旋转角度估计。
为了进一步评估本文算法对JPEG图像局部区域旋转检测与定位的有效性,图6给出了一幅JPEG图像篡改检测与定位实例。首先选取一幅大小为1 500×2 100的未压缩图像,对其进行JPEG压缩得到图6(a)(QF=50、90);然后将图6(a)旋转5°后得到图6(b),利用PhotoShop软件从图6(b)中抠出小鸟并粘贴到图6(a)中,得到篡改后的图6(c),其中篡改区域用白色轮廓线标出;最后对图6(c)进行灰度化处理得到图6(d),利用本文算法进行篡改检测与定位的结果如图6(e)和图6(f)所示。从图6可以看出,本文算法能够有效地检测与定位JPEG图像局部区域的旋转处理,且品质因子越小,其检测与定位效果越好。

图6 图像篡改检测与定位实例(a)原始JPEG图像 (b)旋转角度为5°的图像 (c)合成的篡改图像 (d)篡改图像灰度图(e)QF=50时的检测与定位结果 (f)QF=90时的检测与定位结果Figure 6. An example of image tampering detection and location(a)An original JPEG image (b) The image rotated by 5° (c)The composite tampered image (d)The grayscale version of the tampered image (e)Detection and localization result with QF=50 (f)Detection and localization result with QF=90
4 结束语
本文提出了一种针对小尺寸JPEG图像的旋转角度估计算法,对块效应谱中峰值和旋转角度的对应关系进行分析。JPEG图像被旋转后,其块效应网格随图像旋转而旋转相应的角度。图像纹理边缘的复杂性加大了块效应网格提取的难度,对块效应谱分析带来一定影响,进而导致图像旋转角度估计不准确。首先,利用变异蚁群算法进行JPEG图像的边缘检测并去除以突显块效应;其次,通过交叉差分方式,有效削弱了图像纹理的干扰;再次,通过设定阈值和高斯高通滤波去除无关峰值对坐标轴峰的干扰;最后,通过坐标转换到极坐标形式,依据极坐标中峰值的极角坐标来估计旋转角度。针对旋转角度位于[1°,15°]内的64×64尺寸的JPEG篡改图像,实验结果验证了针对不同质量因子下的JPEG图像,本文方法可以有效地降低估计误差。本文主要探索了图像单次旋转的检测,今后将进一步针对JPEG图像复合重采样(例如旋转后再缩放、缩放后再旋转等)进行研究,探索并利用JPEG图像重采样痕迹进行图像局部篡改检测与定位。

