基于时域模型的电-气综合能源系统分布式鲁棒状态估计

潘 浩，卫志农，黄蔓云，孙国强，陈 胜，孙 康

（河海大学能源与电气学院，江苏省 南京市 211100）

0 引言

随着电力系统和天然气系统耦合关系的不断加深，协同合作、灵活高效的电-气综合能源系统（integrated electricity-gas system，IEGS）开始受到广泛关注，打破了传统多能源系统单独设计、规划与运营的模式，在提升能源使用效率、消纳新能源出力、促进节能减排等多方面发挥着重要作用［1-2］。状态估计（state estimation，SE）作为能量管理系统的基石，为后续IEGS 的潮流计算、安全评估和优化调度提供数据支撑。因此，准确实时的IEGS-SE 具有重要意义［3］。

在电力系统SE 研究［4-5］的基础上，国内外学者计及气网稳态和动态运行的不同工况，开展了较多面向IEGS-SE 的研究。文献［6-9］基于Weymouth方程进行气网稳态建模，适用于时间尺度较长的气网SE 场景；而当系统发生频繁扰动时，相较于电网的快速响应能力，气网较长的暂态过程会使稳态模型产生较大的估计误差，无法满足状态实时跟踪监测、系统安全稳定运行的要求。因此，须构建合适的气网动态SE 模型。

天然气在管道中传输的动态特性遵循流体力学定律，其模型通常由一组质量守恒与动量守恒偏微分方程组描述［3］，难以用解析法直接求解。目前，提出的气网简化模型包括有限元模型［10-11］、“管存”模型［12-13］和统一能路模型［14］等。文献［15］采用Lax-Wendroff 差分法构建气网有限元模型，并提出了基于加权最小二乘法（weighted least squares，WLS）的多时间断面IEGS-SE 方法。文献［16-17］则采用Euler 差分法构建气网有限元模型。文献［16］提出异步分布式IEGS-SE 策略，自适应调整SE 执行周期，实时跟踪系统动态变化。文献［17］将指数平滑法和气网动态模型集成到卡尔曼滤波（Kalman filter，KF）中，并提出时变标量矩阵来克服坏数据影响。文献［18］针对由电、气子系统多时间尺度特性导致的量测时延问题，提出了一种实时IEGS-SE 方法。上述研究均通过有限元差分法将气网偏微分方程转为代数方程求解，但会引入大量时空微元，增加模型复杂度，随着系统规模增大，计算效率大幅下降。文献［14］建立了基于统一能路的气网动态SE模型，将气网由时域映射至傅里叶域计算，兼顾SE精度和计算效率，但在实际工程中须额外增加时域-频域等价转化条件。

鉴于此，文献［19］提出了一种准确刻画气网动态特性以及多时间断面之间状态量传递关系的时域模型，避免了时空微元的递推迭代，在计算效率和收敛性方面具有显著优势。在此基础上，本文提出了基于时域模型的IEGS 分布式鲁棒SE 方法：基于时域模型推导出以真实节点压强为状态量的气网状态空间模型，提高SE 计算效率；提出有限边界信息交互的分布式IEGS-SE 策略，保证子系统隐私安全；采用噪声自适应算法，降低系统波动及量测异常时噪声参数误差的影响。最后，通过仿真算例验证了所提方法的有效性。

1 基于时域模型的气网状态空间建模

1.1 支路时域模型

天然气在管道中进行一维等温传输时，主要满足质量守恒和动量守恒两大定律，其管道内部特性由以下线性偏微分方程组描述［19］：

式中：t和x分别为时间和管道距离；p和q分别为天然气的气体压强和流量；va为气体声速；S、D、λ分别为管道的横截面积、内径和摩擦系数；w为管道平均流速；g和θ分别为重力加速度和管道倾角。

假设在管道水平条件下，不考虑重力加速度g和倾角θ的影响，上述方程组可由统一形式下的线性偏微分方程表示［19］：

式中：u为气网状态量，由气体压强p和流量q构成；K1和K2为常系数矩阵，如式（3）所示。

由于偏微分方程式（2）难以用解析法直接求解，采用中心差商和隐式差分格式将其转换成代数方程近似求解［20］：

式中：下标i和t分别为空间和时间网格编号；μ1、μ2、μ3为常系数矩阵，其解析式见附录A 式（A1）。

代数方程式（4）仅描述了相邻时空微元间状态量的数值关系。而支路状态量的变化本质在于多段时空微元的累积传递，因此，根据式（4）可构建支路首末端状态量u0，t、uM，t的函数关系式如下［19］：

式中：M为支路空间差分段数；ut-1为t-1 时刻支路分段状态量构成的向量，可看作t时刻的初始条件；α和β为常系数矩阵；μ4=μ3+μ-12μ1。

采用气体压强p和流量q表征状态量u，将式（5）由单一支路推广到整个网络，并重新分类排序得到：

式中：p0，t、pM，t和q0，t、qM，t分别为气网各支路首、末端节点压强和流量构成的向量；α1至α4为常系数矩阵；γp，t和γq，t分别为各支路初始条件对pM，t、qM，t的传递分量。此时，式（6）的输入为支路首端状态量和初始条件传递分量，输出为支路末端状态量，构成气网支路时域模型。

1.2 网络时域模型

为构建天然气网络时域模型，需要在支路时域模型的基础上添加天然气网络的拓扑约束，即节点注入流量守恒和支路首末端压强等于所处节点压强两类约束，可表示为：

式中：qn，t为t时刻节点n注入流量向量；Ain和Aout分别为节点-支路流入、流出关联矩阵；pn，t为真实节点压强向量；Apn1和Apn2分别为支路首、末端节点关联矩阵［19］。

利用矩阵分块思想，将式（6）改写为采用支路首、末端节点压强表征支路流量的函数关系式，推导过程见附录B。

式中：K11、K12、K21、K22为常系数矩阵；K0，t和KM，t分别为初始条件对q0，t、qM，t的传递分量。

将式（8）、式（9）代入式（7），可得到天然气网络时域模型为［19］：

式中：Yn为气网广义导纳矩阵；bt为初始条件对qn，t的传递分量。

1.3 气网状态空间建模

气网的状态空间模型主要包括状态方程和量测方程两部分，文献［19］推导的时域模型有助于构建气网量测方程，即式（9）、式（10）。气网量测量包括真实节点压强pn，t、节点注入流量qn，t和支路首、末端流量q0，t、qM，t。因此，以pn，t作为状态量可构建如下量测方程：

而状态方程负责描述相邻时刻状态量的波动变化，提供系统动态的基本信息，若状态方程不准确，在进行预测和更新状态估计值时则会引入更多误差。因此，需要对状态方程进行精确建模，文献［19］中对气网状态方程的建模并未有所探究。

考虑到传递分量γp，t、γq，t与状态量p0，t-1、pM，t-1存在关联，根据式（5）、式（6），可构建其函数关系式如下：

式中：β1至β4为常系数矩阵；λp，t-1和λq，t-1分别为除p0，t-1、pM，t-1外其余初始条件对γp，t和γq，t的传递分量。

结合式（9）、式（14），将bt的解析式（12）改写为：

式中：K31、K32、Yb为常系数矩阵；Kb，t为初始条件对bt的传递分量。上述参数解析式见附录C 式（C1）。

将式（15）代入式（10）得到：

对式（16）进行调整，构建气网状态方程如下：

式中：Fg和Gg，t分别为气网状态转移矩阵和控制变量。计算过程中，Fg为常系数矩阵，与管道参数和运行特性有关；Gg，t与节点注入流量qn，t和传递分量Kb，t有关，其中，qn，t可由Holt 两参数指数平滑法预测获得。

根据式（13）、式（17）构建气网状态空间模型如下：

式中：xg，t=pn，t为气网状态向量；zg，t为气网量测向量；Hg和Bg，t分别为气网量测系数矩阵和初始条件对zg，t的传递分量，其解析式见附录C 式（C2）；wg，t为气网过程噪声向量；vg，t为气网量测噪声向量。

2 基于时域模型的IEGS-SE 建模

在气网建模的基础上，本章进一步构建电网状态空间模型，并以燃气轮机（gas turbine，GT）和电转气（power to gas，P2G）为边界，建立电、气双向耦合模型，为IEGS-SE 提供模型支撑。

由于电网和气网分属不同的管理主体，存在行业壁垒，而海量的用户数据作为电、气子系统能源运营商重要的价值资产，使得隐私和数据安全成为一个更加敏感的话题。因此，需要实时共享全局信息的集中式IEGS-SE 方法难以适用。本文提出的IEGS-SE 方法采用分布式架构保障子系统间通信的安全性与隐私性，并以KF 算法为基础，通过添加过程噪声和量测噪声自适应算法，增强SE 的鲁棒性，实现对IEGS 运行状态的实时精准感知。

2.1 电网状态空间建模

本文建立的电网状态空间模型是一种准稳态模型，适用于系统负荷波动不大、稳态运行的场景。状态方程采用Holt 两参数指数平滑法［21］构建，该方法是一种较为普遍的短期预测方法；而量测方程则与传统电网静态SE 相同。选取节点i的电压幅值Vi和电压相角θi为状态量，量测量包括Vi，节点注入有功、无功功率Pi、Qi以及支路ij的有功、无功功率Pij、Qij。因此，电网状态空间模型可表示为：

式中：xe，t和ze，t分别为电网状态向量和量测向量；Fe，t-1和Ge，t分别为电网状态转移矩阵和控制变量，可通过Holt 两参数指数平滑法获得；h(xe，t)为电网量测方程，见附录C 式（C3）；we，t为电网过程噪声向量；ve，t为电网量测噪声向量。

2.2 耦合元件建模

IEGS 中天然气能与电能一般通过GT 和P2G实现双向传递。GT 通过燃烧天然气产生电能，可平抑电网的负荷波动；P2G 消耗过剩的电能生成氢气，而由于氢气存储和传输困难，需通过化学反应将氢气合成天然气后，注入天然气网络进行大规模存储和传输，实现节能减排。GT 和P2G 输入（生成）气流量和输出（消耗）电功率的函数关系为［22］：

式中：PGT和PP2G分别为GT 和P2G 输出/消耗的电功率；qGT和qP2G分别为GT 和P2G 燃烧/生成的气流量；ςGT和ςP2G分别为GT 和P2G 的能量转换效率；LHV为天然气低热值；ηGT和ηP2G分别为等价后GT 和P2G 的能量转换系数。

2.3 基于时域模型的IEGS 分布式鲁棒SE

2.3.1 分布式IEGS-SE 算法

本文所提的分布式IEGS-SE 算法［16，23］采用去中心化架构，在电、气子系统进行局部SE 后，无需中央处理器协调电、气SE 结果，仅需通过耦合区域边界信息的交互，迭代更新各子系统状态信息，直至边界条件收敛。在此过程中，除耦合区域边界信息交互共享外，电、气子系统的量测信息、状态信息仅受各自数据能量管理中心访问和控制。本文电网为非线性系统，气网为线性系统，分别选择扩展卡尔曼滤波（EKF）和线性KF 作为两个子系统局部SE 的方法。

1）预测步

令k=e，g 分别表示电、气子系统，相应电、气状态预测值和预测协方差矩阵可表示为：

2）滤波步

边界信息交互前电、气状态估计值x̂k，t(0)和估计协方差矩阵Pk，t(0)可表示为：

3）边界信息交互

分布式IEGS-SE 算法在电网和气网间仅存在能量层面的信息交互，不涉及状态信息，所以IEGS中边界信息主要为与GT、P2G 关联的节点注入流量、节点注入有功功率估计值q̂c，t(h)、P̂c，t(h)及其估计协方差矩阵Pgc，t(h)、Pec，t(h)，其中，Pgc，t(h)和Pec，t(h)可表示为：

式中：下标t(h)表示第h次信息交互的时刻；Hgc为气网耦合节点注入流量对应的量测系数矩阵；Hec，t(h-1)为电网耦合节点注入有功功率对应的雅可比矩阵，需在信息交互中实时更新。

具体边界信息交互形式如下：

式中：ξgc=ηcHgc，其中，ηc为能量转换系数构成的对角矩阵；为电网耦合节点注入有功功率的预测值；ξec，t=Hec，t(h-1)；ψec，t=ηcBgc，t，其中，Bgc，t为Bg，t中气网耦合节点注入流量对应的部分。当max|＜υ时，边界信息交互结束，其中，υ为收敛阈值。

2.3.2 过程噪声自适应算法

电网的状态方程通过时间序列预测方法建立，气网的状态方程也须考虑各节点注入流量的预测值，存在一定的建模误差。电、气负荷一直处于波动状态，负荷波动导致状态发生突变，易使过程噪声统计参数变化。若设置过程噪声方差矩阵Qk，t为恒定方差矩阵，则不能正确描述状态方程的预测误差，影响滤波效果，严重时甚至导致运算病态。本文采用一种过程噪声自适应算法［24］，在保证Qk，t满足半正定性的条件下，尽量维持校正信息的完整性，以准确跟踪时变过程噪声参数，表示如下：

式中：dt为权重系数；Dk，t为状态估计值与预测值的差值；Kk，t为卡尔曼增益矩阵；P͂kz，t为量测预测协方差矩阵。

上述参数解析式可表示如下：

式中：o为遗忘因子且0.950 ≤o≤0.995，当系统波动越剧烈时o的取值越大［24］；Rk，t为量测噪声协方差矩阵。

2.3.3 量测噪声自适应算法

受现场环境、运行状态等影响，IEGS 中不可避免地出现通信干扰、仪表故障等异常情况，导致量测噪声参数与真实噪声情况不匹配，KF 算法无法准确修正状态预测值及跟踪系统状态变化。本文基于Huber 的鲁棒M 估计理论［25］，在对量测噪声统计特性进行实时判断后，动态修正Rk，t得到Rˉk，t，以抑制坏数据对SE 的影响：

式中：ϕk，t为修正尺度矩阵，ϕki，t为ϕk，t的第i个对角元素；c为残差阈值［25］，取值通常为1.3～2.0；z͂k，t为量测预测向量；rk，t为归一化量测预测残差向量，rki，t为rk，t的第i个元素。

2.3.4 本文方法整体框架

考虑到电网和气网动态特性的不同，气网的量测采样频率相对较低，在子系统时间尺度允许范围内，设电网、气网SE 周期Δte、Δtg分别为5 min、15 min，且不考虑量测时延影响。

1）当电网须进行SE 时，即时间戳t=teps，se，由于气网的慢动态特性，此时气网无须执行动态SE，仅需单独执行电网EKF。

2）当气网须进行SE 时，即时间戳t=tngs，se，则需在电网、气网各自完成滤波步后，进行边界信息交互，实现状态信息的迭代更新，直至达成边界条件约束。

在SE 过程中，噪声自适应算法并不改变KF 算法原有架构，仅添加噪声估计步骤以跟踪调整噪声参数，能够较好贴合动态SE 场景，计算方便、额外工作量小。基于时域模型的IEGS 分布式鲁棒SE框架如图1 所示。

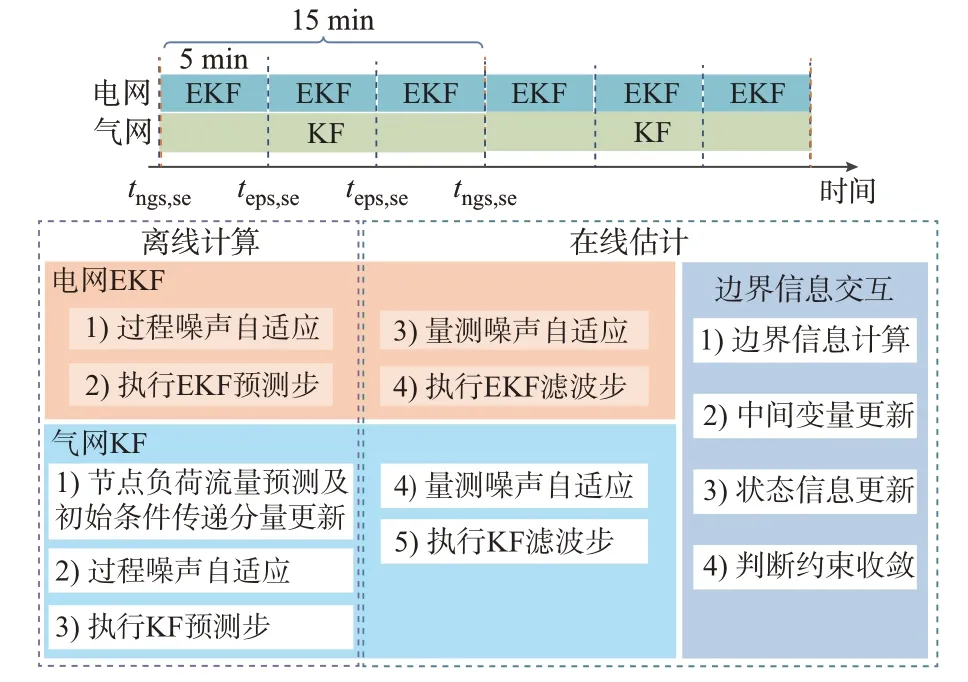
图1 基于时域模型的IEGS 分布式鲁棒SE 框架Fig.1 Framework of distributed robust IEGS-SE based on time-domain model

3 算例分析

本文基于IEEE 24 节点电力系统和修改的比利时20 节点天然气系统［26］构建IEGS-SE 算例，共包含39 条输电线路、21 条管道和2 座加压站，IEGS 通过2 台GT 和2 台P2G 设备耦合，系统拓扑如图2 所示。假设加压站为电驱动类型，其功率消耗对电网影响较弱。因此，仅考虑其对气网节点压强的约束，可将加压站末端节点等效为虚拟节点处理。

仿真实验中，设耦合元件GT 和P2G 能量转换效率分别为40%、60%，则GT和P2G的能量转换系数分别为20.776（MW·s)/kg 和86.567 (MW·s)/kg。气网管道摩擦系数和气体声速分别设为0.002 和340 m/s。气网差分空间步长和时间步长分别设置为2 km 和15 min。初始情况下估计协方差矩阵和过程噪声协方差矩阵的对角元素均设为10-6。气网潮流真值通过文献［19］的方法计算获得，IEGS 中电压、气压量测通过在潮流真值的基础上叠加相对标准差为0.005 的高斯白噪声来获得，功率、流量量测则通过叠加相对标准差为0.01 的高斯白噪声来获得。仿真环境建立在Intel Core i7-10700 CPU 和16 GB RAM 的计算机上，通过MATLAB 2016b 进行求解。

3.1 IEGS-SE 滤波性能测试

本文中IEGS-SE 仿真总时长为24 h，在全量测配置且量测误差服从高斯分布条件下进行SE。以IEGS 电网节点1 至5 支路首端无功功率和气网节点1 注入流量量测为例，结合量测值、估计值与真实值的相对误差进行分析，仿真结果如图3 所示。可见，量测量的相对估计误差明显小于量测误差，说明本文方法具有良好的滤波效果。

图3 IEGS 量测估计结果Fig.3 Measurement estimation results of IEGS

在IEGS 参数设置相同的情况下，采用控制变量法评估过程噪声及量测噪声自适应算法对本文方法SE 效果的影响。设置如下4 种方法：

M1：两种自适应算法均采用，即本文方法；

M2：仅采用过程噪声自适应算法；

M3：仅采用量测噪声自适应算法；

M4：未采用噪声自适应算法。

各场景进行500 次蒙特卡洛仿真实验后，引入状态量的均方根误差均值衡量滤波效果：

式中：F为蒙特卡洛仿真次数；T为时间断面数；m为状态量数量；x̂i，t和x̑i，t分别为状态量估计值和真实值的第i个元素。

仿真结果如表1 所示。由表1 可知，当量测服从高斯分布时，M1 和M2 方法由于采用过程噪声自适应算法，滤波效果更优，而M3 和M4 方法效果相对下降。可见，在动态SE 过程中，过程噪声自适应算法增强了对时变噪声参数的跟踪能力，能有效提升滤波性能；而量测噪声自适应算法在遇到部分正常量测数据时序波动较大时，为保证SE 的鲁棒性，会主动修正其对应的噪声参数，降低其对估计结果的影响，导致误差略微增大，但对整体滤波性能影响不大。

表1 不同自适应算法下的估计结果Table 1 Estimation results with different adaptive algorithms

3.2 分布式IEGS-SE 性能测试

为测试本文采用的分布式算法对IEGS 滤波效果的影响，表2 给出了在参数设置不变和两种噪声自适应算法均采用的情况下，各子系统单独SE 时的状态量RˉMSE和采用文献［15］中提出的集中式IEGS-SE 方法所测得的状态量RˉMSE。

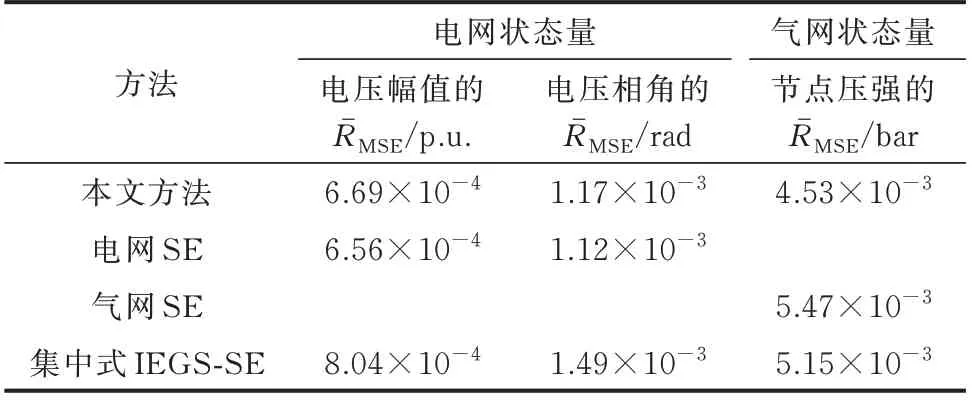
表2 不同估计策略下的估计结果Table 2 Estimation results with different estimation strategies

图4 展现了不同估计策略下电、气耦合量测相对估计误差。结合表2 和图4 可知，相较电网和气网单独进行鲁棒SE，分布式IEGS-SE 通过交替迭代达成边界条件收敛后，气网滤波效果有较为明显的提升。这是因为电网量测冗余度高，SE 精度相对较高，在边界信息交互过程中，通过耦合约束将高精度的电网SE 结果转化为气网的冗余量测，可改善气网SE 精度；而采用气网SE 结果作为电网的冗余量测时，由于气网SE 精度相对较低，对电网的滤波效果提升较弱。与文献［15］的方法相比，本文方法精度优势主要在于采用预测辅助的SE 方法，预测信息一定程度上增加了量测冗余，并使用噪声自适应算法增强了系统状态的跟踪能力。

图4 不同估计策略下耦合量测相对估计误差Fig.4 Relative estimation errors of coupling measurements with different estimation strategies

3.3 IEGS-SE 抗差性能测试

为测试本文方法在坏数据影响下的抗差性能，假设6～8 h 时IEGS 中电网节点2 至4 支路首端有功功率和气网节点10、11 支路首端流量量测丢失（即量测值为0），进行动态SE。图5 展示了IEGS 量测丢失下的SE 结果。若不添加量测自适应算法，6～8 h 时丢失量测下对应的估计值将大幅偏离真实值，而本文方法在此期间仍能较好地跟踪系统状态变化。

图5 IEGS 量测丢失下的估计结果Fig.5 Estimation results with measurement loss of IEGS

为进一步说明本文方法抗差性能的普适性，除较为严重的量测数据丢失外，当量测受通信干扰或仪表故障影响时，量测误差也将远大于正常量测噪声。假设每个时间断面下，坏数据在潮流真实值基础上叠加10 倍标准差的高斯白噪声随机生成，数量占子系统量测的1%～5%。在不同坏数据比例下，进行500 次蒙特卡洛仿真实验，并使用RˉMSE来评估方法的抗差性能，仿真结果见表3。

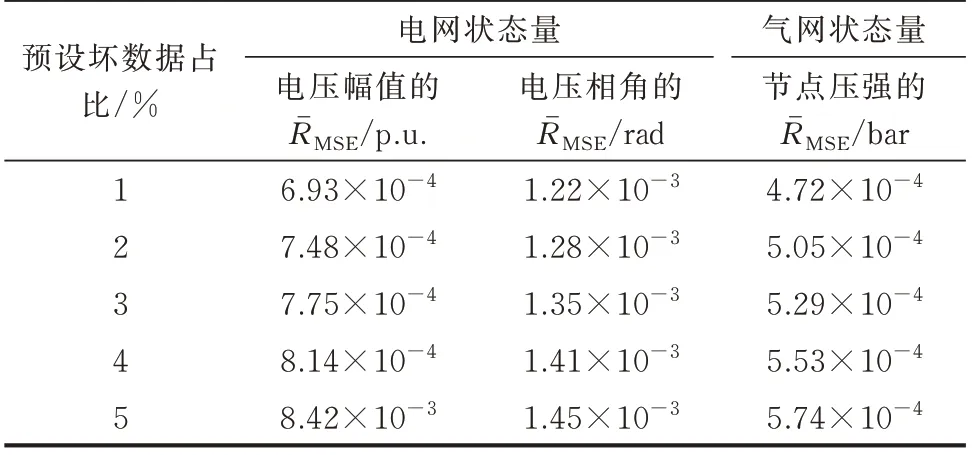
表3 不同坏数据比例下的估计结果Table 3 Estimation results with different bad data ratios

由表3 可知，随着坏数据比例的增加，IEGS 状态量的RˉMSE会有所上升，但仍能维持在同一数量级，与正常量测下估计结果相比数据波动不大。其主要原因在于，基于Huber 的鲁棒M 估计理论能在各时间断面的滤波步中实时判断并更新量测噪声的统计特性，若发现可疑量测数据则会降低其对SE的影响。因此，本文方法在面对坏数据干扰时，具有良好的鲁棒性。

3.4 IEGS-SE 计算效率测试

本文所提的IEGS-SE 方法分为在线估计和离线计算两部分：在线估计指IEGS 收到实时量测信息后进行电网和气网滤波步计算，并通过交互迭代达成边界条件收敛；离线计算指电网和气网的预测步，因为其仅涉及历史状态信息或负荷预测信息计算，无须占用实时算力资源。表4 列出了单时间断面下本文方法SE 各步骤计算耗时，并与文献［15］所提方法进行对比。

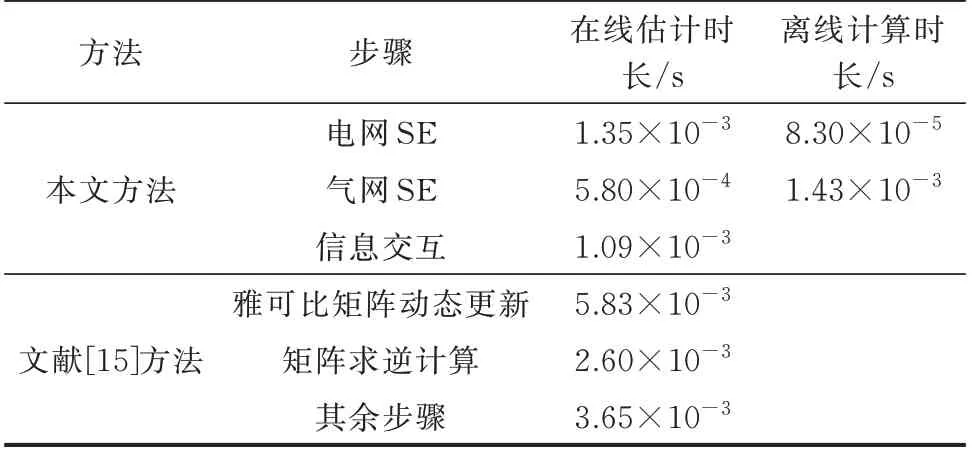
表4 IEGS-SE 计算效率统计数据Table 4 Statistical data of calculation efficiency for IEGS-SE

如表4 所示，本文方法在SE 计算效率方面具有明显优势，整体在线计算时间仅需约3×10-3s，相较文献［15］所提方法缩短了75%。具体原因如下：1）模型差异，文献［15］采用有限元差分模型状态变量较多，矩阵计算规模大，导致计算效率下降，以气网差分空间步长2 km 为例，差分模型含所有节点（包括虚拟节点）压强和管道分支流量在内的544 个状态量，而时域模型仅有真实节点压强在内的18 个状态量，在线计算简便；2）方法差异，文献［15］基于WLS 构建IEGS-SE 模型，只有在接收到实时量测信息后才能进行实时SE，因此，该方法没有离线计算时长。此外，由于集中式SE 的状态数量较多，单时间断面下IEGS-SE 通常需要迭代4～5 次才能达到收敛阈值，雅可比矩阵动态更新和矩阵求逆计算耗时长，而本文采用分布式策略，仅使用部分耦合边界信息在初始滤波步的基础上迭代修正状态量，如式（24）所示，迭代1～2 次即可达成边界条件收敛，避免了全局SE 的低效。

值得注意的是，由于气网采用状态空间模型，需在预测步中实时更新初始条件（即传递分量），因此，离线计算时长相较电网预测步略长。综上所述，本文所提气网状态空间模型在大规模IEGE-SE 应用中具有良好的工程价值，实现了气网模型的简化和降维，缩小了系统状态量的规模，能够通过离线计算减少在线估计的工作量，提高计算效率，满足调度人员实时监管的需求。

4 结语

为实现对IEGS 动态过程全面实时的感知，需要着重考虑电、气状态空间建模及其联合动态估计建模方法。本文提出了一种基于时域模型的气网状态空间模型，在保证计算精度的前提下，解决了传统有限元差分法计算复杂度高的问题。在此基础上，引入动态分布式策略和噪声自适应算法构建了IEGS 分布式鲁棒SE 模型，并给出了相应的求解方法。仿真算例表明：

1）所提模型具有良好的滤波效果，噪声自适应算法可有效跟踪过程噪声参数变化，抑制IEGS 量测坏数据影响，提升SE 精度；

2）分布式策略能够保证子系统通信交互隐私安全，保证耦合量测SE 结果满足边界条件约束，改善气网的滤波效果；

3）通过算例对比，证明本文基于时域模型提出的IEGS 分布式鲁棒SE 方法在计算效率方面具有显著优势，为大规模IEGS-SE 实时应用奠定了基础。

由于本文方法根据气网线性偏微分方程原理进行状态空间建模，当各管道流速在设定平均流速附近波动时，本文方法有较高精度；而对于气网负荷波动较大的场景可能会产生一定范围内的误差。因此，后续将在SE 流程中设计兼顾计算代价与估计精度的管道流速自适应更新步骤。此外，耦合元件精细化建模、电气量测时延、异步估计策略、线路参数不确定性等因素对IEGS-SE 的影响也需要深入探索和研究。

附录见本刊网络版（http：//www.aeps-info.com/aeps/ch/index.aspx），扫英文摘要后二维码可以阅读网络全文。