基于深度强化学习的新型电力系统调度优化方法综述

冯 斌，胡轶婕，黄 刚，姜 威，徐华廷，郭创新

（1.浙江大学电气工程学院，浙江省 杭州市 310027；2.之江实验室，浙江省 杭州市 311121）

0 引言

新型电力系统是以确保能源电力安全为基本前提，以绿电消费为主要目标，以坚强智能电网为枢纽平台，以源网荷储互动及多能互补为支撑，具有绿色低碳、安全可控、智慧灵活、开放互动、数字赋能、经济高效基本特征的电力系统［1］。随着“碳达峰·碳中和”目标的提出，新能源在电力能源供给中的占比逐渐增加，将形成新能源占比逐渐提高的新型电力系统［2］。未来，电力占终端能源形式的比例需提高至80%［3］，非化石能源在生产侧的占比要达到80%，光伏、风电等清洁能源装机容量势必逐年增长。新能源的广泛接入与迅速发展使得新型电力系统的随机性、不确定性显著增加，这给传统的调度优化方法带来了极大的挑战。

强化学习（reinforcement learning，RL）拥有强大的自主搜索和学习能力，与监督学习、无监督学习并称现今3 种机器学习范式［4］，其侧重于学习实现目标的最优策略。而深度学习（deep learning，DL）［5］通过多层的网络结构，可以对高维数据特征进行抽取，更侧重于对事物的特征提取与感知理解。结合RL 与DL 的深度强化学习（deep reinforcement learning，DRL）在适应复杂状态环境的同时，能够无需依赖于预测数据即可实现在线实时的调度控制，目前已经在游戏［6］、围棋［7］、机器人控制［8］、城市智慧交通［9］、ChatGPT 智能对话等领域得到了广泛应用，在很多场景下甚至能够超越人类表现。

DRL 起源于动态规划，其实质是解决一个动态优化问题，理论源于动态规划与马尔可夫决策过程（Markov decision process，MDP），相较于启发式搜索算法更具备理论基础。DRL 作为一种数据驱动方法，能够从历史经验中学习决策调度方法，针对非线性、非凸问题具有很好的自适应学习决策能力。目前，大多通过无模型的算法处理，避免了对不确定实时变化的物理模型进行建模，适用于复杂多变的场景。相较于其他传统优化方法，DRL 对同一问题模型的不同数据具有更好的泛化能力，以及在相似问题之间具有更好的迁移性，并已在电网频率控制［10］、电压控制［11］等领域得到应用。

本文从DRL 原理出发，对DRL 算法在新型电力系统调度中的应用现状进行了总结。

1 新型电力系统调度问题

随着新能源接入比例的提高、电网规模的不断扩大，为提高系统整体运行的经济性与可靠性，应协调调度电网的发电资源与用电资源。新型电力系统中的调度问题是为了解决电力系统供需平衡的高维、不确定性强的优化问题。其中，电力系统经济调度（economic dispatch，ED）、最优潮流（optimal power flow，OPF）和机组组合（unit commitment，UC）问题是电力系统运行中的3 个关键问题。

1）经济调度问题是以最小化电力系统的总运营成本为目标、满足电力需求和各种运行约束的优化问题。传统的经济调度问题是在满足功率平衡和机组功率边界的前提下，确定各火电发电机组的有功出力，使得总燃料耗量（发电成本）最小。随着新能源出力不确定性的增加，系统的约束条件更加复杂、不确定性更强。

2）最优潮流问题［12］是指在满足电力系统潮流等式约束，以及节点电压、线路潮流、发电机爬坡等不等式约束的情况下，在主网中实现发电成本最小或在配电网中实现网损最小的优化问题。最优潮流与经济调度问题的区别主要在于是否考虑电力系统潮流等式约束。新型电力系统所含风电、光伏等间歇性新能源使得电力系统最优潮流问题，尤其是交流最优潮流问题［13］的求解更加复杂。

3）机组组合问题是在满足系统负荷需求和其他约束条件时实现系统运行成本最小的机组启停计划优化问题。随着大量新能源接入，机组组合方案繁多，不确定性增加，求解更加困难。

传统的优化调度方法往往需要对系统做出一系列假设，同时也难以应对系统动态变化的挑战。随机优化、鲁棒优化、分布式鲁棒优化、启发式优化算法等传统优化算法被用于解决新型电力系统的不确定性问题，但它们都依赖于精准的预测，难以应对新能源出力与负荷需求多变的场景。随机优化常通过采样、机会约束生成等方式将不确定性问题转化为确定性问题，但是算法复杂度随着场景的增加而增加；鲁棒优化通过给出不确定集的方式解决不确定性问题，但是通常其给出的优化结果仅面向最恶劣的场景，过于保守；启发式优化算法，如遗传算法、粒子群算法等，容易陷入局部最优，而且动作复杂度的增加给启发式的优化算法带来严重的维数灾问题，难以稳定收敛。

DRL 因其实时决策、不断反馈修正的特性，能够更好地应对新型电力系统新能源的不确定性，可为新型电力系统调度问题提供新的解决途径。

2 DRL 原理

2.1 从RL 到DRL

RL 借鉴了行为主义心理学，是一类特殊的机器学习算法。与监督学习和无监督学习的回归分类目标不同的是，RL 是一种最大化未来奖励的决策学习模型，通过与环境交互建立的MDP［14］解决复杂的序列决策问题。RL 中常见的概念包括智能体、环境、状态（state，S）、动作（action，A）、奖励（reward，R）。如图1 所示，智能体处在环境中，执行动作后获得一定的奖励，而环境由于智能体执行的动作发生状态的变化。依据每一步获得的奖励，通过特定的算法最大化未来的累计奖励是RL 算法的核心。详细RL 原理见附录A。

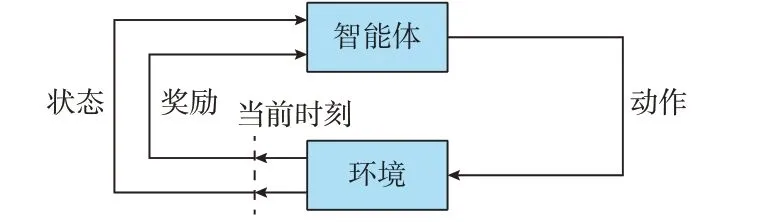
图1 智能体与环境的交互过程Fig.1 Interaction process between agent and environment

在传统的RL［15］中，一般可以通过迭代求解贝尔曼最优方程获得最优动作价值函数与状态价值函数，进而指导智能体做出选择。但是在实际场景下，存在着迭代效率低、计算代价大等问题。为此，通常采用参数化的神经网络来近似估计最优动作价值函数和状态价值函数，这也就形成了DRL。

2.2 DRL 算法

依据是否有模型，将DRL 算法分为基于模型的DRL 和无模型的DRL。其中，基于模型的DRL 是指智能体可以学习到环境动态变化的参数。在无模型的DRL 中，依据智能体的动作选择方式，又可分为基于价值、基于策略、执行者-评论者的算法，其中，执行者-评论者算法也可以看做是结合了基于价值与基于策略的算法。

2.2.1 基于模型的DRL 算法

基于模型的DRL 算法需要对环境进行建模，然后，基于模型给出策略选择或者动作规划，因而其采样效率较高。该环境通常指状态转移模型，即真实环境的动态变化模型。

结合无模型微调的基于模型的RL［16］（modelbased RL with model-free fine-tuning，MBMF）是一种基于学习到的环境进行模型预测控制的算法。MBMF 首先基于数据集训练神经网络动态模型去学习环境；然后，针对该动态模型执行模型预测控制，并将控制器产生的运行结果进一步添加到神经网络动态模型中进行训练。重复整个迭代训练过程，直至MBMF 达到所需的性能表现。

AlphaZero［17］是一种利用已有环境的基于模型的DRL 算法。它是AlphaGo［7］的改进，可实现从围棋到各类棋类游戏的智能博弈，通过自主学习环境规划搜索策略。AlphaZero 与MuZero［18］通过蒙特卡洛树搜索（Monte Carlo tree search，MCTS）［19］对所学习得到的策略函数进行搜索，实现了动作的多样性探索。

2.2.2 基于价值的DRL 算法

基于价值的DRL 算法是通过迭代或者训练得到最优动作价值函数，智能体依据最优动作价值函数选择获得最大的最优动作价值函数所对应的动作，从而实现了策略选择。常见的基于价值的DRL算法包括深度Q 学习（deep Q-learning，DQN）［6，20］及其改进算法、优先经验回放［21］、Double Qlearning［22］、Dueling DQN［23］和值分布RL 算法中的C51［24］以及Rainbow DQN［25］等。

最早提出的RL 算法是基于价值的Q 学习［15］与状态-动作-奖励-状态-动作（state-action-rewardstate-action，SARSA）［26］算法，它们是通过采用最优贝尔曼方程更新Q 值表的方式，迭代得到最优动作价值。

随后，文献［6，20］将卷积神经网络（convolution neural network，CNN）与传统RL 算法中的Q 学习算法结合，提出了DQN 模型。为避免蒙特卡洛更新带来的巨大方差问题，DQN 采用时间差分算法更新最优动作价值函数，更新目标如式（1）所示。

式中：yt为t时刻由时间差分算法得到的目标动作价值；rt为动作得到的奖励；γ∈[0，1]为奖励衰减因子；Q(st+1，at；wt)为动作价值的神经网络函数；st+1为t+1 时刻的状态；at为t时刻的动作；wt为t+1 时刻神经网络参数。

随后，为解决DQN 过高估计最优动作价值函数的问题，在Double DQN［22］中引入目标网络，在Dueling DQN［23］中采用竞争架构分别估计优势函数和状态价值函数。采用差异化的优先经验回放［21］提高训练效率，添加高斯噪声以提高动作的探索能力［27］。为充分利用动作价值函数的分布信息，进一步提出了分布式价值的C51 算法［24］以及学习分布分位数值的分位数回归深度Q 学习（quantile regression DQN，QR-DQN）算法［28］，以及结合上述所有改进的Rainbow DQN［25］算法。

虽然Rainbow DQN 算法在离散动作空间的游戏策略问题上取得了不错的效果，但是只能针对离散动作空间进行建模。对于实际问题中常见的连续动作空间则需要进行离散化处理，可能会造成一定动作空间的损失和维数增多的问题。

2.2.3 基于策略的DRL 算法

基于策略的DRL 算法也可称作是基于策略梯度的DRL，相较于基于价值的DRL，其策略函数可以直接映射到连续动作空间，对于连续控制问题具有更好的效果。

基于策略的DRL 是通过最大化奖励较高动作的出现概率，实现未来期望奖励的最大化。这是一种端到端的学习方式，直接优化策略的期望奖励。常见的基于策略的RL 算法有：经典的策略梯度RL算法［29］、置信域策略优化（trust region policy optimization，TRPO）［30］算法、近端策略优化（proximal policy optimization，PPO）［31］算法等。

在基于策略的DRL 中，采用参数为θ的神经网络来代替策略函数。策略梯度表示形式如式（2）所示。

式中：g为策略梯度值；R为奖励；b为不依赖于动作的基线；st为t时刻的状态；T为该情节所经历的时间步；π(at∣st；θ) 为策略函数。 梯度项logπ(at∣st；θ)为希望将情节获得的奖励向上提高的梯度。

参数更新时将在现有参数θ上加上αg，实现梯度上升，其中，α为学习率。上述训练过程将最大化较高奖励动作的出现概率。

RL 算法［29］使用蒙特卡洛方法更新策略梯度，具有较好的稳定性，但是采样效率较低，会带来较大的估计方差。为此在策略学习中减去基线，可有效减少方差。由于基于策略的RL 对步长十分敏感，上述方法难以直接选择合适的步长，如果新旧策略差异过大则不利于学习。TRPO［30］通过约束限制新旧策略动作的KL（Kullback-Leibler）散度，避免了策略发生过大参数更新步的情况，解决了策略梯度更新步长的问题。而PPO［31］则通过模型自适应地调整新旧策略动作的KL 散度，以保证策略梯度的稳定更新。但是TRPO 和PPO 都是采用同步更新策略的算法，其每次更新都需要采样大量样本，算法复杂度高、训练效率低，并且其应用也需要大量算力支撑。

2.2.4 执行者-评论者DRL 算法

执行者-评论者DRL 算法中的执行者算法类似于基于策略的DRL 算法，评论者算法类似于基于价值的DRL 算法。因此，执行者-评论者DRL 算法同时学习策略和价值函数，其框架图如图2 所示。执行者-评论者也可以被认为是一种基于策略的DRL 算法，特殊之处在于它使用了状态价值函数作为式（2）的基线b，减小了方差，即Aπ(st，at)=Qπ(st，at)-Vπ(st)，其中，Qπ(st，at)为动作价值，Vπ(st)为状态价值。Aπ(st，at)也被称为优势函数，若优势函数大于0，则表示该动作优于平均值，是合理的选择。

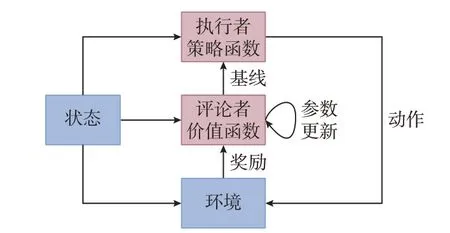
图2 执行者-评论者DRL 算法框架Fig.2 Framework of actor-critic DRL algorithm

它既结合了基于价值和基于策略DRL 算法的优点，也在一定程度上继承了二者的缺点。常见的执行者-评论者DRL 算法包括确定性策略梯度（deterministic policy gradient，DPG）算法［32］、深度确定性策略梯度（deep deterministic policy gradient，DDPG）［33］算法、柔性执行者-评论者（soft actorcritic，SAC）［34］算法、异步优势执行者-评论者（asynchronous advantage actor-critic，A3C）［35］算法、双延迟确定性策略梯度（twin delayed deep deterministic policy gradient，TD3）算法［36］等。

DPG 每次确定性地探索一个动作，降低了采样需求，能够处理动作空间较大的问题，但为保证未知动作的探索能力，必须采用异步策略更新方法。DDPG 在DPG 的基础上借鉴了DQN 在Q 学习基础上改进的思想，利用深度神经网络拟合DDPG 中的Q 函数，采用异步的Critic 估计策略梯度，使训练更加稳定简单。TD3 在DDPG 的基础上引入了性能更优的Double DQN，并通过取2 个Critic 之间的最小值避免过拟合，解决了过高估计以及方差过大的问题。过高的估计会使得更新方向与理想情况有偏差，而方差过大会使得训练不稳定。SAC 建立在非策略最大熵RL 框架［37］上，在实现策略预期回报最大化的同时也具有最大熵，可提升算法的探索能力。

上述异步策略更新算法可以在策略更新时重复利用过去的样本，对样本利用效率高。目前，常见的异步策略更新的DRL 算法，均是以DPG 为基础的确定性策略算法，如DDPG、TD3 等。但是，基于确定性策略的算法对超参数敏感，收敛难度较大。A3C 中有多个智能体在中央处理器（central processing unit，CPU）多线程上异步执行，使得样本间的相关性很低。因此，A3C 中也没有采用经验回放的机制，而是直接采用同步策略更新机制。

2.2.5 多智能体与分层DRL 算法

在DRL 的基础上，结合多智能体、分层级等理论，提出了一些适用于更加复杂场景的DRL 算法。

1）多智能体DRL 算法

考虑到现实复杂的实际环境中，往往不止一个动作发出者，即有许多智能体通过共同交互信息实现合作或竞争，其主要目标是实现共同奖励的最大化与多智能体之间的均衡。早期的多智能体RL，考虑多智能体之间的互相博弈提出了Nash-Q 学习算法［38］，这类算法需要大量的存储空间存储Q 值，适用于规模较小的问题。

近年来，随着DDPG、A3C 等算法拥有更优的性能表现，目前，多智能体DRL 大多基于执行者-评论者算法框架，其中，最具有代表性的是多智能体深度确定性策略梯度（multi-agent deep deterministic policy gradient，MADDPG）［39］和反事实基线的多智能体执行者-评论者［40］。它们均采用集中式训练、分布式执行的算法模式，利用所有状态信息集中训练出评论者，每个智能体仅采用自身观测到的信息，执行各自的动作。在智能体动作执行期间，解决了多智能体间信息及时共享的问题。在新型电力系统调度问题中，常见的多区域电网、微电网（microgrid，MG）、综合能源系统都可以采用多智能体DRL 算法进行求解。

此外，在基于价值分解的多智能体DRL 算法中，多个智能体通过简单加和局部价值函数［41］或采用非线性混合网络［42］联合价值函数，将各主体观测到的局部价值函数合并为联合价值函数。因此，此类算法大多用于共同合作问题。

2）分层DRL 算法

一个复杂问题往往会有庞大的状态空间与动作空间，导致实际奖励是非常稀疏的，而分层DRL 算法的提出将改善奖励反馈稀疏的问题。分层DRL［43］可以在一些复杂的DRL 任务环境下，将最终任务转变为多个子任务的形式，实现DRL 任务的分解。通过各子主体策略来形成有效的全局策略。

经典分层强化学习方法是将复杂问题建模为半马尔可夫过程，底层策略建模为MDP 问题。经典的分层强化学习算法包括Option［44］、分层抽象机（hierarchies of abstract machines，HAMs）［45］、

MAXQ［46］算法等。当今，结合深度学习的分层DRL算法采用2 层结构：上层结构每隔一段时间进行调用，根据调用时观测到的状态，给出下层子任务；下层结构作为底层结构，根据当前目标状态和子任务产生动作。例如，分层DQN［47］的双层均采用DQN网络，上层制定一个下层能够实现的小目标并由下层网络实现，待小目标实现后或达到指定时间后，重复指定新的小目标；子策略共享分层DRL 算法［48］将子策略参数共享，以提升子任务的训练效率。文献［49］将分层DRL 算法应用于多微电网经济调度模型，实现了长短期利益结合的分布式经济调度。

3 DRL 在新型电力系统调度中的应用分析

将DRL 应用于新型电力系统调度问题时，需要定义DRL 中的智能体、环境、状态、动作以及奖励。智能体指动作的发出者，也可认为是系统运行人员；环境指电力系统；状态指环境中各个设备当前的运行状态，如发电机上一时刻出力、电热功率需求、风光实时功率、目前所处的时段等；动作指系统中可以人为控制调节的变量，如发电机出力、储能等；奖励通常是需要实现的目标，如最小化系统运行成本、最大化新能源消纳、最小化电压频率偏差等。关于DRL 应用于新型电力系统调度的文献详见附录B。

3.1 经济调度问题

在经济调度问题中需要决策的变量均为连续变量。因此，常采用DDPG、A3C、PPO 等具有连续动作空间的DRL 算法。

1）大电网

针对含有风光储的大电网经济调度问题，文献［50］在考虑备用的情况下，采用DDPG 应对风光荷不确定性以实现系统的动态经济调度，但DDPG 不能够实现异步采样。文献［51］依据电网调度运行指令下发的实际特点，考虑联络线功率、风电场出力，采用A3C 算法实现多场景并行学习的智能经济调度。

当涉及多区域电网经济调度问题时，由于模型复杂，涉及动作空间大，常采用多智能体的算法降低动作空间复杂度。文献［52］提出的基于通信网络架构（CommNet）的分布式多智能体DRL 算法，在训练过程中可使各区域智能体间无须共享光伏、负荷预测数据和设备参数等信息。为避免有效决策信息的损失，文献［53-54］没有利用预测信息，直接采用端到端决策来进一步提升调度的经济性。

2）微电网

针对含有风光储的微电网经济调度问题，文献［55-59］的动作对象均为储能充放电，实现的目标分别为光储充电站收益最大化、微电网经济稳定运行、负荷需求与发电功率的精准匹配、最小化运行成本（并网）和尽量满足负荷需求（孤岛）。文献［59-60］都考虑能源出力的随机性，构建了运行期望最小化奖励函数。考虑到多微电网的动作空间维度以及学习复杂度，需要采用分层分布式的方式实现在线经济调度［49］。

3）虚拟电厂

针对含有风光储的虚拟电厂（virtual power plant，VPP）经济调度问题，文献［61］将工业用户中的可控负荷作为一种调度资源，考虑了光伏、风电、微型燃气轮机的环保与经济成本，基于A3C 算法的三层边缘计算框架实现经济运行策略的高效求解。文献［62］考虑了储能系统，基于对抗生成网络生成的场景数据集以及DDPG 算法实现虚拟电厂的鲁棒经济调度。但上述文献并未考虑响应信号在虚拟电厂内部的分解，文献［63］则考虑了上级总的响应信号分解问题，并采用锐度感知最小化算法［64］，提升了算法对环境和奖励的鲁棒性。

4）综合能源系统

在含有热、电、天然气等综合能源系统（integrated energy system，IES）经济调度问题中，文献［65］采用DDPG 算法使综合能源系统中的热电联供机组的电功率、燃气锅炉输出的热功率、储能的充放电功率的经济调度动作空间处于连续状态。由于DDPG 对超参数敏感且动作空间探索不足，采样效率较低，文献［66］采用SAC 算法，解决了电-气综合能源系统中天然气系统利用传统优化方法难以凸化和收敛的问题，可有效应对源荷不确定性，并实现RL 智能体模型秒级优化调度决策。

考虑到DRL 算法对复杂动作空间探索难度大，文献［67］采用双层RL 模型，上层采用RL 算法实现电池出力调度，下层采用混合整数线性规划求解综合能源系统经济调度问题，避免了约束作为惩罚项带来的DRL 算法复杂度增加问题，提升了模型计算效率。

然而上述方法在保证约束的安全性上仍有一些欠缺，需要采用一些保障安全的算法。文献［68］采用循环神经网络构建新能源预测模型［69］，并引入了安全引导函数来保障策略的安全性，实现了综合能源系统的安全低碳经济运行。

相较于大电网、微电网、虚拟电厂，综合能源系统可以实现多能源利用互补。例如，通过热电联供机组实现电力和热量的同时生产；通过燃气锅炉输出热功率；通过电转气单元将电力转换为气体。随着需要控制的设备种类及参数增多，动作空间也将增加，会导致神经网络的训练收敛速度下降，甚至造成维数灾难。多智能体DRL 作为一种有效处理多智能体参与的决策方法，也逐渐在大规模综合能源系统的经济调度问题中得到应用。文献［70］将综合能源系统中的多个利益主体建模为多智能体，文献［71-72］将多综合能源区域（园区）建模为多个主体，而文献［73］将电力系统和热力系统分别建模为2 个主体。它们均取得了比单一智能体DRL 算法更优的收敛速度和经济效益。同时，通过集中训练分散执行的算法流程，可以解决各利益主体之间数据共享的问题。

3.2 最优潮流问题

文献［74］将传统Q 学习算法应用于电力系统最优潮流计算领域，实现电力系统有功、无功、多目标的最优潮流计算。

但是，传统的Q 学习采用离散动作，会损失一部分动作空间，为此需要采用基于策略或者执行者-评论者的DRL 算法。文献［75］基于CloudPSS 仿真云平台，验证了基于DDPG 的最优潮流计算的可行性；由于DDPG 中的评论者网络难训练、不稳定，文献［76］虽然基于DDPG 算法构建了执行者网络，但没有使用评论者网络，而是基于拉格朗日数学解析推导得到了确定性梯度。由于PPO 相比于DDPG具有更高的采样效率、更稳定的学习策略，以及更容易调节的超参数，文献［77-78］采用基于模仿学习的PPO 算法求解交流最优潮流问题。

前述的最优潮流问题是针对主网的，而配电网由于没有大型发电机组，其研究对象是在满足潮流约束的同时，通过潮流合理分配使得网损最小。文献［79］基于PPO 算法控制储能有功功率、无功功率以及风电的无功功率，实现了在不违反电压和电池储能容量约束的情况下配电网网损的最小化。文献［80］采用完全分布式的PPO 算法，实现了不平衡配电网的光伏有功功率最大化输出与电压稳定。

针对互联的微电网，由于其动作空间大，传统单一智能体算法难以满足计算需求，需要建模为多智能体DRL 问题求解。文献［81］依据智能体的连续离散动作空间，设置了双层DRL，并将潮流等式约束设置在环境中；文献［82］将潮流等安全约束构建成梯度信息，保证最优控制策略产生安全可行的决策方案。

由于并不是所有场景下的调度问题都是非凸的，可以将凸的子问题抽离出来，构建优化问题与DRL 结合的双层求解结构。文献［83］将居民微电网的最优运行成本问题建模成混合整数二阶锥的优化问题，并将其转化为MDP 主问题与最优潮流二阶锥优化子问题，主问题采用MuZero［18］算法得到较优的在线优化结果。文献［84］针对互联微电网在信息不全情况下的潮流能量管理问题，考虑在配电网层面只能获取公共连接点（point of common coupling，PCC）处的功率信息，设计了双层算法。在上层基于改进的Q 学习实现互联微电网购售电成本最优，在下层针对单个微电网实现最优潮流。文献［81］虽然也采用了双层DRL，但实际上是将离散动作空间和连续动作空间作为前后2 层DRL 的决策空间。

安全约束最优潮流［85］增加了可靠性约束来确保电力系统能够承受一定预想故障的冲击。由于安全约束最优潮流需要搜索预想故障集，如果采用基于优化的交流最优潮流，其计算量也非常大；而DRL 方法的提出，将有助于在交流最优潮流的基础上实现安全约束最优潮流。文献［86］以最小化约束越限为奖励，以提升系统在各种随机场景下的N-1安全性为核心，采用A3C 算法结合电力领域知识在减小负荷削减量的同时降低了系统运行成本。

DRL 算法能够在一定程度上解决电力系统交流最优潮流的精确求解问题，尤其是在非凸约束增多时，优化求解复杂度会急剧提升。而DRL 在处理类似问题时可以进行精确建模，而不必为实现凸优化而损失模型精度，甚至可以得到比凸松弛后的交流最优潮流优化问题更经济的解。此外，DRL 算法在需要大规模搜索时也有一定优势。

由于最优潮流问题需要考虑潮流等式约束，因而相较于经济调度问题，其动作空间受到一定的限制，这也是当前基于DRL 算法求解最优潮流的难点。这需要保证在潮流等式约束被满足的同时，处理新能源出力的不确定性并寻求最优发电调度计划。现阶段文献主要将潮流等式约束放在环境中处理，较少文献将潮流等式约束融合至策略产生的约束中，形成安全的策略［82］。

3.3 机组组合问题

文献［87］采用RL 算法求解机组组合问题，而文献［88］采用分布式Q 学习算法，因仅涉及局部通信，提高了求解的鲁棒性。但是，Q 学习算法的动作空间受Q 表格的限制，难以处理高维动作状态。为此，文献［89］采用深度神经网络逼近Q 函数的DQN算法实现高维机组组合动作空间的探索。为应对新能源出力的不确定性，文献［90］针对随机波动的光伏出力，采用全连接神经网络拟合Q 值求解考虑光伏出力的机组组合问题。

由于机组组合的动作空间随着机组数量而急剧增长，在现有文献中，Q 学习算法最多仅能应用于含12 台机组的算例。为进一步克服机组动作空间随机组数量呈几何增长的问题，文献［91］采用引导树搜索方法实现了对动作空间的快速高效搜索，可求解30 台机组组合问题，相比于混合整数线性规划算法，可减少机组的频繁动作，并在降低系统运行成本的同时减少了负荷损失概率。

通常在机组组合问题中，除决策机组启停的离散量外，还需要同时给出机组出力的连续决策变量。文献［89，91］采用Lambda 迭代法进行求解；文献［88］将机组组合和经济调度问题建模为一个问题，将连续机组出力作为动作对象，动作空间则满足机组启停等约束。文献［92］采用SAC 确定机组启停计划，然后通过Cplex 求解器求解单时段优化问题得到机组出力。而文献［87，90］并未提及机组出力的决策过程。

在机组组合问题中，机组启停动作空间是一个离散的动作空间。采用诸如DQN、PPO 等一般的DRL 算法难以有效应对机组数增加而带来动作空间维度呈指数增长的问题。因而，基于一般的DRL算法仅能够解决机组数较少的机组组合问题，并且较少涉及新能源接入。但一般的DRL 算法对环境的探索能力有限，需要结合树搜索算法或者智能体提前预知一定的环境模型信息，进而提升或引导智能体对高维动作空间的探索效率。

机组组合问题作为一个长时间序列决策问题，即使采用先进的DRL 技术也难以实现较好的决策，目前在仿真算例中仍存在较多的问题亟待解决。其中，一个较为关键的问题是用电计划无法完全被满足。在理论研究中，常将用电计划满足程度表述为失负荷风险。由于机组组合的动作空间极大，在机组数量较多、测试时间较长的情况下，失负荷通常是不可避免的。因此，后续的研究重点是改进动作空间的建模形式或采用学习能力更强的算法等以确保用电计划完全满足。

3.4 应用前景分析

由于电网对于安全性和供电可靠性要求较高，实际落地应用不可能一蹴而就。考虑到决策的稳定性、安全性以及误决策的危害，可以先在配电网或用户侧进行一些尝试，然后，再从小区域低电压等级慢慢推广到大区域高电压等级。在配电网侧，由于涉及的设备种类多样、波动性较大，对于算法的实时性要求高，可以采用DRL 算法进行实时经济调度、设备出力控制、电压控制等，以实现配电网众多设备的安全实时经济运行。在用户侧，可以实时获取价格信号和屋顶光伏等新能源出力信息，采用DRL 算法实时控制需求响应、家用电器、温控负荷等。文献［93］将RL 算法应用于美国科罗拉多州一个包含27个家庭的微电网中， 应用结果表明，采用RL 算法可大幅度降低用户用电成本，实现秒级别的优化控制。文献［94］采用拟合Q 迭代算法实现电热水器的控制。该项目是住宅需求响应试点项目的一部分，其中，10 台电热水器用于直接负荷控制，每台电热水器配备了8 个温度传感器和1 个可控功率加热装置。在试点项目中，相比于恒温控制器，采用RL算法可使电热水器的总能耗成本降低15%。2021年5—6 月，上海某写字楼中央冷水机组采用RL 算法控制冷却机组和冷却水泵来重设定点温度［95］，实现了近似专家系统的控制效果，并验证了RL 决策系统的鲁棒性、稳定性和学习速度。

在大电网侧，随着新能源广泛接入，源荷波动愈加剧烈，系统对于日内实时优化的需求上升。可以先采取数据接入、辅助决策方式进行试点运行。如果在试点过程中出现错误，则需要对算法进一步校验，必要时可以增加一些人工调度经验规则，采用数据知识混合驱动的方法保证决策的正确性。常见的实时调度场景包括日前和日内的实时计划动态快速调整、电力市场实时的报价出清策略等。文献［96］所研发的电网脑于2019 年11 月部署在中国江苏电网调控中心安全Ⅰ区。电网脑能在满足调控需求的前提下，在20 ms 内对电压、潮流越界等问题提供解决方案，快速消除风险，同时降低约3.5%的网损。该成果可用于辅助调度员对电压与联络线潮流进行控制，进一步可作为全自动化调度的基础技术手段。

在海量数据场景下，DRL 作为一种数据驱动的决策方案，能够在保证目标最优性的同时更快速地求解目标函数，获得比传统方法更高效经济的策略［86，91］。例如，在风险评估中，DRL 可以快速搜索高风险级联故障［97-98］，也可以将DRL 与电力系统运筹优化方法深度结合，通过DRL 加速优化计算或者实现精确建模与求解。

4 研究方向展望

DRL 算法能够对智能体进行针对性训练，并能够根据场景的变化快速求得最优管理策略，满足电网运行的实时性要求。但DRL 作为一种基于深度神经网络的算法，需要大量学习仿真数据，并且所得到的结果较难解释。电力系统调度是电力系统的核心环节，一般不允许出现差错。若DRL 在电力系统调度中获得应用，还需要在以下方面做进一步深入的研究。

1）建立真实的电网仿真环境

DRL 需要大量学习仿真数据。在电力系统中，通常需要单独搭建适配于电力系统的环境，智能体在与环境交互的过程中，产生大量情节，这也就是DRL 需要学习的仿真数据。DRL 的目标是最大化奖励，因此，可以通过奖励的设置对违反的约束给予惩罚，将需要实现的经济性、安全性目标设置在奖励中。考虑到DRL 的训练需要搭建类似于Gym［99］的电网环境，当前已有不少开源工作者构建了类似的开源环境库，例如，Gym-ANM［100］、PowerGym［101］、Grid2op［102］等。未来，需要基于数字孪生，搭建电网仿真系统，加强数字资源的积累，为应用提供基础。

2）算法性能的提升

随着建模对象和环境逐渐复杂，在大规模复杂环境下DRL 收敛求解时间也会随之增加。如果在实际中求解一个大规模复杂新型电力系统调度问题时，必然会遇到维度灾难问题。当动作空间维数过大时，可搜索的动作空间将很大，进而影响DRL 收敛速度和动作的准确性。此外，如果是类似机组组合问题的0-1 离散变量过多，也会加剧DRL 训练的难度。随着DRL 理论的不断发展，未来可以考虑引入模仿学习、元学习的思想［103］，以便缩短复杂环境下智能体的培训时间，提高性能。

在与环境交互计算方面，当前智能体与环境的模拟交互过程以及数据的传输通信仍然是通过CPU 完成的。如果能够开发类似于Isaac Gym 的图形处理器（graphics processing unit，GPU）环境，环境的模拟和神经网络的训练都将置于GPU 内，使得数据直接从内存传递到GPU 的训练框架中（如PyTorch），不受CPU 数据传输限制，则将大大加快目前的训练速度，进一步提高DRL 求解大规模复杂问题的性能。

3）安全性研究

由于DRL 方法输出的决策存在不确定性，其安全性不如传统优化算法，可能会给出不符合电网安全运行的结果，这时便需要算法有能力给出规避机制，实现电力系统的安全稳定运行。对于新能源全部消纳的要求，可以允许存在一定的弃风弃光，但在有严格物理安全约束要求时，如果DRL 不能够完全确保得出的决策满足安全约束，将会导致系统安全问题。当前许多研究基于DRL 的调度文献未涉及系统安全约束的问题，即使是涉及系统安全性的文献，也基本是将约束建模成奖励函数惩罚项的形式，极少从数学理论上证明DRL 算法可满足安全约束条件。也有将约束在建模过程中直接融合在MDP过程中，形成安全可靠的DRL 算法。进一步，也可尝试采用安全RL 算法［104］保证策略操作的安全性。

4）可解释性研究

传统基于价值或基于策略的DRL 算法，具备强逻辑性和可解释性。但神经网络模型也被称为黑盒子模型，缺乏一定的解释性。而DRL 是在RL 的基础上，引入了神经网络来拟合价值函数或（和）策略函数，对复杂问题的建模具有更好的实验效果。但是，神经网络的引入不利于其可解释性，难以在实际应用中从原理上说服调度人员依据DRL 算法给出的决策进行操作。未来，可结合可解释性机器学习给出可解释性的策略动作，提升DRL 的可解释性，让调度人员更易于接受人工智能算法的决策结果。

5）迁移性和鲁棒性研究

目前，研究性论文中智能体所处的环境都是电力系统仿真模拟环境，数据均为理想化的数据，不存在数据干扰的情况。而在实际运行的电力系统环境下，如何保证DRL 算法的正确性、保证模型的鲁棒性是值得考虑的问题。文献［63］通过使用锐度感知最小化［64］实现了噪声的鲁棒性，此外，在DRL 算法领域也出现了鲁棒DRL 算法［105］，这也是未来可以尝试的解决方法。

5 结语

本文介绍了新型电力系统调度问题，阐述了基于模型、基于价值、基于策略和执行者-评论者的DRL 算法原理，以及在调度中可尝试应用的DRL算法。在经济调度问题中，分别从大电网、微电网、虚拟电厂、综合能源系统角度总结了DRL 应用的结果；在最优潮流问题中，以交流最优潮流模型为基础，总结了主网、配电网、微电网以及安全约束最优潮流问题的DRL 解决方案；在机组组合问题中，总结了火电发电机组的机组组合和考虑新能源的机组组合问题。最后，分析了当前应用前景，并论述了未来研究方向。

本文受国家自然科学基金项目（52007173,U19B2042）资助，谨此致谢！

附录见本刊网络版（http：//www.aeps-info.com/aeps/ch/index.aspx），扫英文摘要后二维码可以阅读网络全文。