基于ADDPG策略的超立方体卫星编队控制

苗峻,涂歆滢,殷建丰,彭靖,李海津,陈子匀

1.中国空间技术研究院 钱学森空间技术实验室,北京 100094

2.中国空间技术研究院 北京空间飞行器总体设计部,北京 100094

3.中国人民解放军66136部队,北京 100042

1 引言

卫星编队通过彼此协同工作可以完成单一卫星难以完成的空间任务,具有灵活性高、功能多和容错性强的特点[1-2],而高精度的卫星编队可以大幅提高对地观测的精度,可广泛应用于地球重力场观测、地磁观测等需要超高精度对地观测的科学任务中[3]。由于高度集成化和自动化技术快速发展,卫星市场需求量不断扩大,大规模卫星编队的研发和部署掀起前所未有的热潮[4]。

目前针对高精度编队控制算法,常见的方法有模型预测控制[5]、模糊控制、滑模控制以及LQR控制等[6],然而现有研究主要集中在针对较小规模卫星的高精度编队方法进行研究。文献[7]提出了一种基于非线性干扰观测器和人工势函数的分布性协同控制方法,对4星组网卫星编队控制进行了仿真验证。文献[8]在考虑避障的情况下,基于特殊的人工势能函数设计了一种航天器编队自适应协同控制律,以1颗主星3颗从星的4星组网航天器编队为例进行了分析仿真;文献[9]提出一种基于Lyapunov 方法的自适应控制器,可以消除初始编队构型误差补偿外界扰动,维持编队期望构型,并在双星编队中进行了仿真验证;文献[10]提出了一种自适应滑模变结构连续控制方法,并在双星编队上进行了验证;文献[11]针对“一主三从”的4星静止轨道卫星编队构型保持,提出了一种管道模型预测控制方法,实现了卫星编队的鲁棒控制;文献[12]提出了一种网络李雅普诺夫算法,并在“一主三从”的4星编队上取得了良好的闭环控制效果;文献[13]基于随机矩阵理论,针对4星多智能体卫星编队设计了一种分布式无模型自适应迭代学习控制算法,将卫星编队控制在期望误差内;文献[14]针对双星编队提出了一种最优控制策略;文献[15]提出了一种编队弹性控制策略,以减少编队控制的能耗,延长编队寿命,并应用于10颗卫星的较大规模编队。通过对近期相关文献的分析可以看出,目前在卫星大规模高精度编队控制方面的研究还不够完善,所涉及问题的规模都比较小。

近年来,深度强化学习结合了深度学习和强化学习(RL)优点,大大提高了RL的性能。更进一步的,为了提高算法解决复杂问题的能力,2016年DeepMind团队提出了基于actor-critic 双重网络框架的深度确定性策略梯度算法(deep deterministic policy gradient,DDPG)[16]。DDPG结合了DQN(deep Q networks)算法的特点,构造非常简单,仅需要一个基本的 actor-critic 框架和只需要进行微调的学习算法,就能提高训练效率,较好地完成在高维连续动作空间中的行为决策[17],因此被引入到导弹制导一体化控制[18]、无人机控制[19-20]、舰船自动控制[21]等多种领域。但相关技术在卫星编队控制领域研究较少[22-23]。

现有的文献很少研究较大规模卫星编队,传统方法直接应用于大规模编队控制器太复杂,精度不高或者控制策略较难以大规模应用,而深度强化学习方法在连续动作的控制上表现优异,可以很好地解决类似编队卫星的连续控制。本文首次提出了一种基于吸引法则的深度确定性策略梯度ADDPG编队控制算法,旨在探索一条新的可用于大规模卫星高精度编队控制方法。通过充分挖掘利用已有信息,利用深度强化学习简单结构网络延展解决复杂问题的能力,设计了基于虚拟中心的编队控制奖励函数、状态空间、动作空间,在满足高精度编队需求的同时,尽可能减少编队卫星能量消耗,实现大规模高精度卫星编队“又精又省”控制,为未来地球重力场观测、地磁观测等需要超高精度对地观测的科学任务进行技术储备。

2 超立方体拓扑结构

理想的网络拓扑具有对称性高、容错性好等特点,与其它的网络模型相比,超立方体拓扑结构具有结构简单、连通度高、容错性和扩展性强等诸多优越性质,便于实现卫星大规模物理组网。针对超立方体的拓扑结构可以减少大规模编队通信时间延迟,大幅度提高编队卫星间通信效率。

超立方体编队卫星之间的拓扑信息关系使用加权无向图来表示。加权无向图G=(V,E,A)由节点集V={υ1,…,υn},边集E⊆V×V和n维加权邻接矩阵A=[αij]组成。若图G中的每个节点的度都为k,则称图G为k正则。

n维超立方体(记为Wn)是一个无向图,可以定义为:Wn=,V为含2n个节点的集合,每个节点都可以用一个n位二进制字符串来表示,即为该节点坐标。H为Wn中不相交的边集。Wn中当且仅当两节点坐标有且仅有一位不同时,有边相连。

超立方体W1、W2和W3如图1所示,4维超立方体W4如图2所示。Wn是正则的,共有2n个节点和n2n-1条边,每个节点都有n个邻接点。

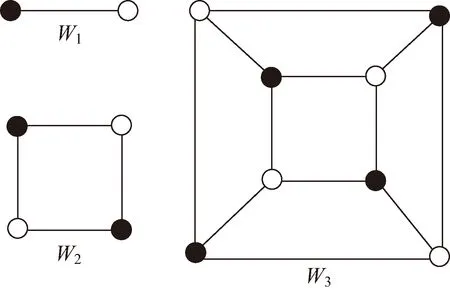
图1 超立方体示意

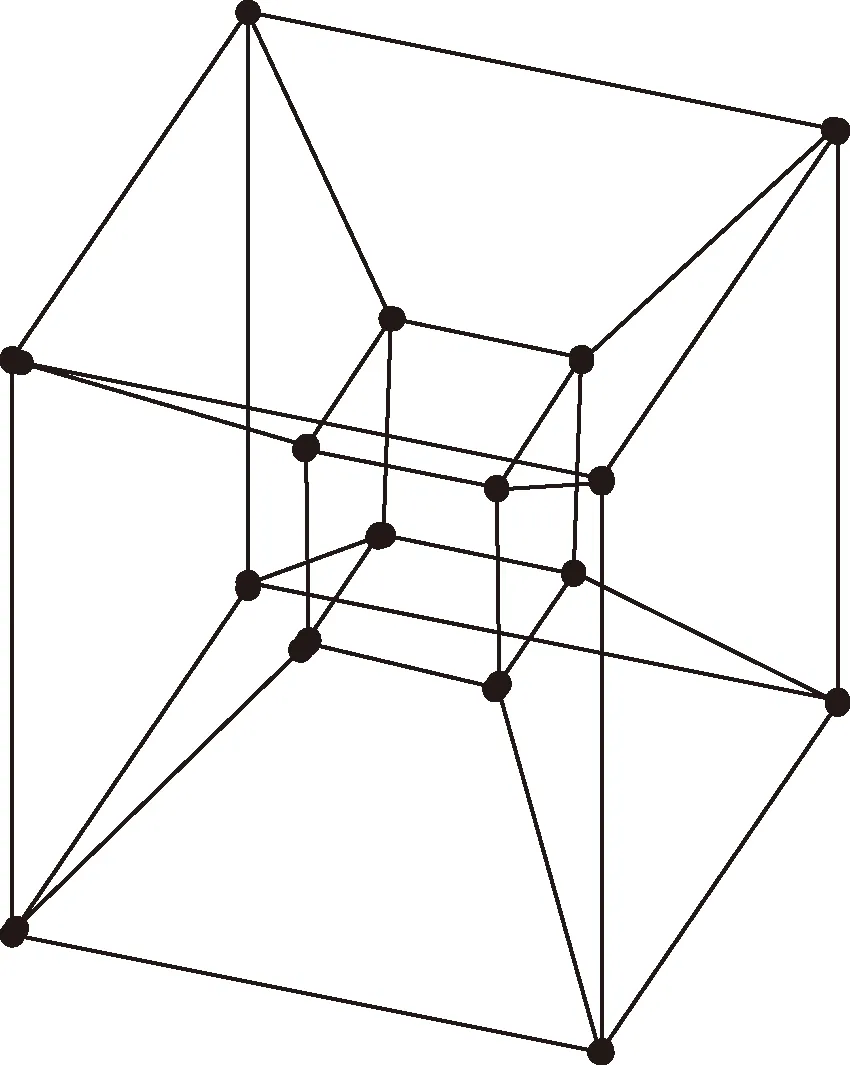
图2 四维超立方体示意

在大规模卫星编队系统中,超立方体拓扑结构具有高度冗余通信链路和扩展的能力。

1)容错性。在大规模的卫星编队中,每当有节点卫星或通信链路出现故障,就有可能会导致整个卫星系统任务失败。在n维超立方体拓扑结构中,网络中任意两个不同节点之间均有n条不相交的平行路径。

2)扩展性。例如两个9维超立方体网络W9之间仅通过增加一条链路,就可以形成10维超立方体网络W10,可以通过低维超立方体网络不断组成更高维超立方体。因此可以通过节点卫星构建子超立方体网络,后续再逐级构建不同等级规模的卫星编队网络,具有良好的嵌入性和扩展性。

3 卫星编队动力学模型

卫星编队的空间相对运动使用Hill坐标系,如图3所示,Ti表示第i颗卫星的位置,定义x轴指向卫星的运动方向,y轴垂直于轨道平面,z轴指向地心。经过推导可以得到卫星运动的C-W方程:

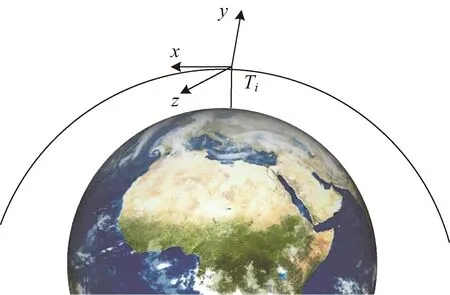
图3 卫星运动示意

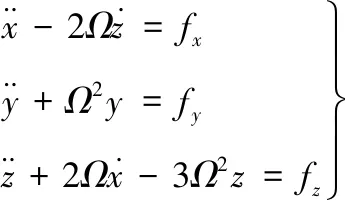
(1)

式(1)易于求出近似解析解,得到卫星相对运动轨迹,是本文构型设计的基础。通过设计合理初值,可得卫星编队的构型,可应用于圆轨道或近圆轨道,编队半径为几百米到几十千米的编队半径远小于轨道半径的编队。

式中:

4 编队虚拟中心设计

大规模卫星组网编队控制的目的分为对编队卫星构型整体相对于预期轨道的控制,以及组网编队中各子卫星的轨道保持。为了反映编队整体的运动状态和趋势,保证编队整体不会“ 漂移”,结合传统多智能体控制中领航-跟随者和虚拟结构两种思想,设计编队“虚拟中心”去衡量编队的整体状态,为基于ADDPG的控制策略设计奠定基础。

在超立方体卫星编队中节点集V={υ1,…,υn}中每一个节点代表一颗小卫星,根据一致性理论,多智能体卫星编队中节点数目有限,若其中任意互为邻域节点的两个节点信息达成一致,则多智能体卫星编队达成一致。信息一致性的过程具有空间Markov性,而Markov随机场等同于Gibbs随机场,故事件节点υ1取得状态ηi的概率可写为Gibbs分布:

式中:T是分布中熵的度量,在编队系统中可用势能的均方差表示编队的失衡程度。

U(ηi)是一个能量函数,定义为:

U(ηi)=D1(ηi)+∑D2(ηi,ηj)

式中:D1为单节点势能函数;D2为双节点势能函数。

D1(ηi)=(‖ηi-〈ηc〉i‖-dic)2

D2(ηi,ηj)=(‖ηi-ηj‖-dij)2

式中:dic为连通图的直径。根据平均场理论,某一特定节点受邻域内其他所有节点的影响,可以用一个平均作用近似获取,则节点υ1及其邻域的虚拟中心〈ηR〉i可以定义为:

如图4所示,以4维超立方拓扑为例,16颗卫星分为4个子方形编队,即图中蓝色方形。通过虚拟中心设计确定每个子编队的虚拟中心的目标点和路径,其中每个蓝色方形编队的虚拟中心,即为蓝色大方形的顶点,此处不设置实际卫星。4维20星超立方体卫星编队可以用于对地重点目标高精度立体观测、多个密集重点目标多重观测以及陆地海洋快速运动目标的高精度识别确认和预警。

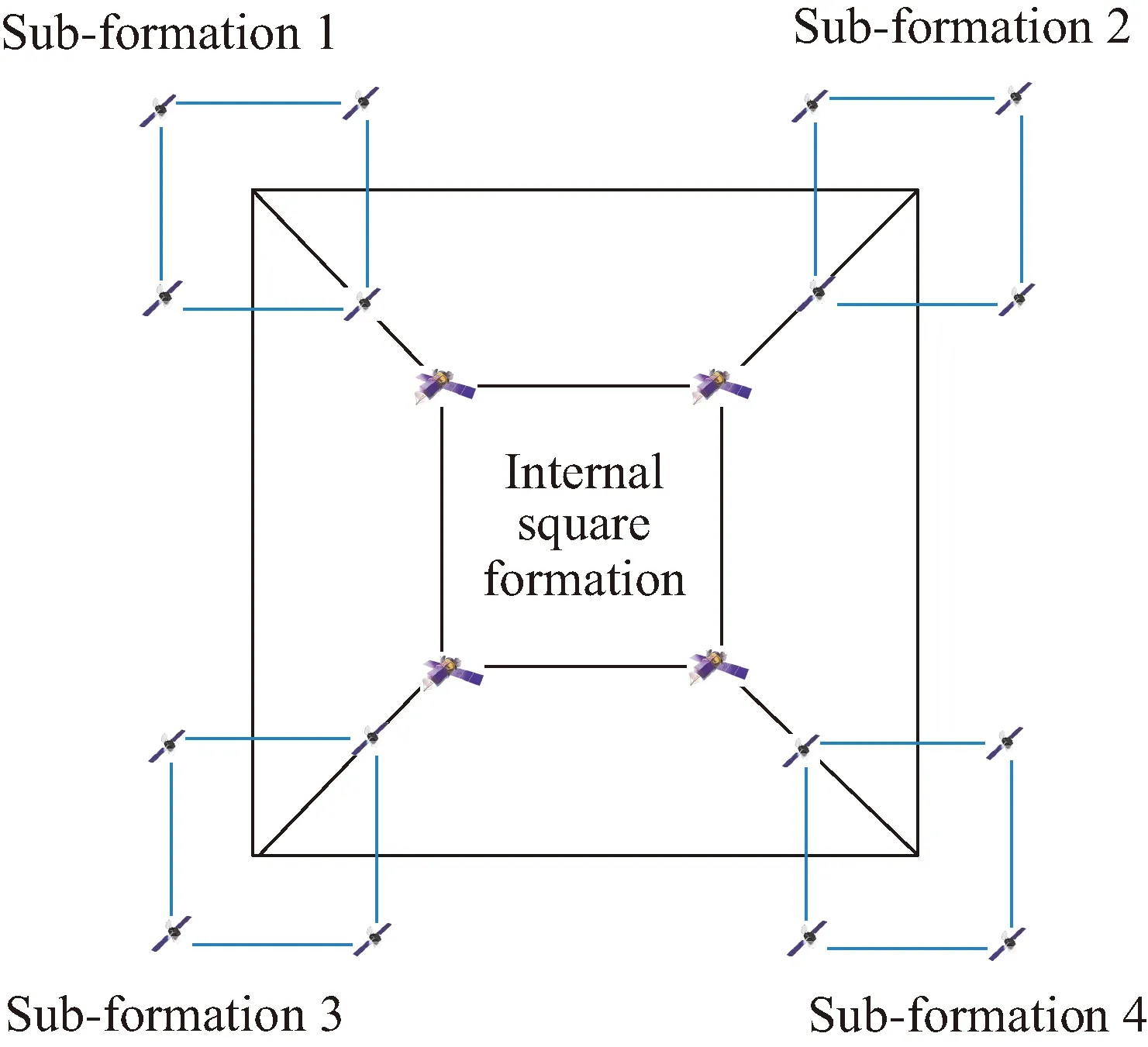
图4 超立方体拓扑结构编队

5 基于ADDPG算法的编队控制策略

设计好的卫星编队构型会受到模型误差、空间摄动力以及随机干扰等各种因素影响,要保证稳定的构型以顺利完成任务,需要进行编队控制使得编队卫星的状态偏离保持在任务允许的误差范围内。

DDPG 算法是一种融合了基于值迭代和策略迭代的深度强化学习算法[24]。可以针对任意大小的状态空间和行为空间进行最优策略的学习,在与环境的交互过程中,根据环境状态、动作和奖励得到最优策略,使卫星编队具有更好的性能表现。

DDPG网络架构由在线动作网络、目标动作网络、在线评价网络、目标评价网络4个网络组成。将策略网络和价值网络分别拷贝一份作为目标网络,实时与环境交互的网络称为在线网络。基于DDPG算法的编队控制问题可以用(s,a,p,r)框架形式进行表示。其中s为状态集;a为动作集,是编队卫星执行机构行动空间的集合;p为状态转移概率;r为奖励函数。

5.1 状态空间和动作空间

状态集s由编队内各卫星的三轴方向的位置和速度组成。状态空间s如下:

s={(ux,uy,uz)i,(vx,vy,vz)i}

(2)

动作空间:卫星的轨道控制通过装在各卫星上的轨道推力器提供冲量实现。

定义动作空间a={ax,ay,az},其中

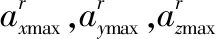
5.2 设计奖励函数Reward

强化学习过程是智能体在与环境交互过程中获得最大奖励的过程。满足编队构型精度要求的基础上考虑能耗。引入一致性协调控制的相关思想,将位置、速度误差结合成为一致误差,定义编队综合误差为:

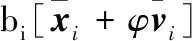
(3)

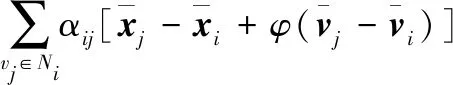
从航天器编队的功能属性本质要求分析,其一方面应满足编队的构型任务要求,另一方面应尽可能满足构型保持过程中的能耗。

奖励函数是各编队卫星在环境中执行动作得到的奖惩反馈信号,奖励函数设计如下:

r(s,a)=∑γ1ei+∑γ2ai

(4)

式中:γi(i=1,2)为各成分在奖励函数中的权重;ei为编队综合误差(负);ai为当前状态下采取的行动,即卫星控制力。关于γi(i=1,2)的选取参考如下。

γ1:训练首先要保证编队的整体期望构型和个体期望状态,γ1选取比较小的数值,当训练结果保证编队精度后可以适当增大取值。

γ2:类似终端奖励,初始可以设置较大的值,参数值过大可能无法到达控制目标,参数取值过小有可能导致控制能耗过高。

5.3 ADDPG算法

在DDPG中,每个状态-动作对都有相对应的一个Q值,通过反复迭代学习计算选择执行状态对应的最大Q值下的动作,并获得按该行动策略执行下的回报值,不断尝试各状态可能执行的动作,使Q值不断趋向于最优。要取得较高的回报,行动策略应按最大Q值所对应的动作执行,然而,当算法处于初期,在不断学习迭代的过程中,Q值存在一定波动,不能完全精准地评估状态-动作对的回报。当算法处于学习中期阶段时,完全执行最高Q值对应的动作,即算法一直处于扩张状态,可能使得算法陷入局部最优。探索是寻找并执行即使当前评价不是最优,但从长期来看回报最大的动作,可以给出帮助算法跳出局部最优的策略,然而如果算法一直处于探索状态,将会大幅降低系统的学习效率。

为提高DDPG的学习效率,本文提出ε-吸引策略,采用ε-attraction动作选择策略平衡探索与扩张。吸引策略,是指编队内卫星会被精度比它高的其他卫星吸引,模仿精度比他优异的其他卫星的状态和动作,并参考其状态更新自己的动作。

考虑随着卫星i距离卫星j越远,其面对的环境对卫星j的参考性越弱,定义ψij为编队卫星i与卫星j的相对距离,则卫星i与卫星j的吸引力βij(ψij)表示为:

(5)

式中:β0为最大吸引力,通常取β0=1;ζ∈[0.01,100]为吸引系数,标志吸引力变化。

ADDPG充分融入已学习信息进行探索,通过引入探索率ε使系统以概率ε进行探索,以1-ε选择当前Q值最高对应的动作。

当编队卫星以ε的概率从动作集合选择动作时,卫星参考优异的编队卫星的状态信息和选择动作,而不是盲目地随机选择。ε-attraction动作策略a*表示为:

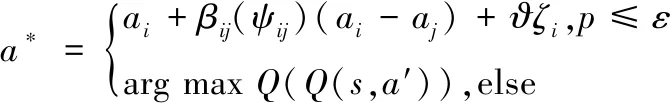
(6)

式中:ϑ为常数,一般取ϑ∈[0,1];arg maxQ(Q(s,a′))为状态s下选择最大Q值的动作;ζi为高斯分布的随机数;p为探索扩张概率,p∈[0,1]。

5.4 网络结构深度确定性梯度通行策略求解方法

采用ADDPG 算法实现超立方体卫星编队控制,编队卫星在与环境的不断交互控制中学习控制策略,更新网络参数。同时根据ε-attraction动作选择策略调整动作a,得到回报函数值r和下一时刻系统状态s′。交互过程中所产生的信息(s,a,r,s′)均被保持到经验池中。

其中,在线动作网络更新策略梯度为:

∇θμJ≈Est～ρβ{∇θμQ(s,a∣θQ)∣s=st,a=μ(st∣θμ)}=

Est～ρβ{∇aQ(s,a∣θQ)∣s=st,a=μ(st)·

∇θμμ(s∣θμ)∣s=st}

式中:∇θμQ(s,a∣θQ)∣s=st,a=μ(st∣θμ)为策略网络对动作a的梯度值;θμ为在线策略网络的参数。在线评价网络采用最小化损失函数完成更新过程,损失函数L定义为:

式中:yi=ri+γiQ′(si+1,μ′(si+1|θμ′)θQ′)。

在线网络定期将学习好的权重参数复制给对应的目标网络,通过软更新的方式更新目标网络参数。

目标动作网络为:

θμ′=λθμ+(1-λ)θμ′

式中:θμ′为目标策略网络的参数;λ为软更新率。

目标评价网络更新方式为:

θQ′=λθQ+(1-λ)θQ′

式中:θQ为在线价值网络的参数;θQ′为目标价值网络的参数;式中λ为远小于1的参数,由于是采取“软更新”的方式,可以实现目标网络的参数循序更新,增强网络的稳定性,保证ADDPG 算法稳定性提升。

6 仿真与分析

编队卫星参数:长20cm、质量1kg的立方体卫星,仿真实飞环境考虑地球扁率、大气阻力、太阳光压、日月引力等摄动干扰。编队构型整体在太阳同步轨道上运动,利用编队间的稳定几何关系,实现高精度对地观测等任务。

卫星初始位置的轨道根数分别为:半长轴7078.137km,偏心率e=0.0010441,轨道倾角i=98.1880°,近地点幅角ω=90°,升交点赤经Ω=0°。

编队中内部小方形边长1000m,即编队半径707m;外部子编队虚拟中心应处于3000m边长方形上,即编队半径2121m;外部子编队为边长1000m方形,即相对于子编队自身虚拟中心编队半径707m;卫星编队构型同图4,ADDPG算法参数设置见表1。

表1 ADDPG算法参数设置

20颗卫星进行组网和编队保持的位置误差变化、速度误差变化以及控制加速度分别如图5～9所示,图5和图6分别为采用ADDPG方法编队中4个子编队中各卫星的位置误差以及内部正方形编队和虚拟中心的速度误差,图7和图8分别为采用4个子编队中各卫星的速度误差以及内部正方形编队和虚拟中心的速度误差。图中蓝、红、橙、紫线分别代表该子编队内序号1到4的组网卫星状态信息。图10描述了20颗组网卫星的三维相对位置。

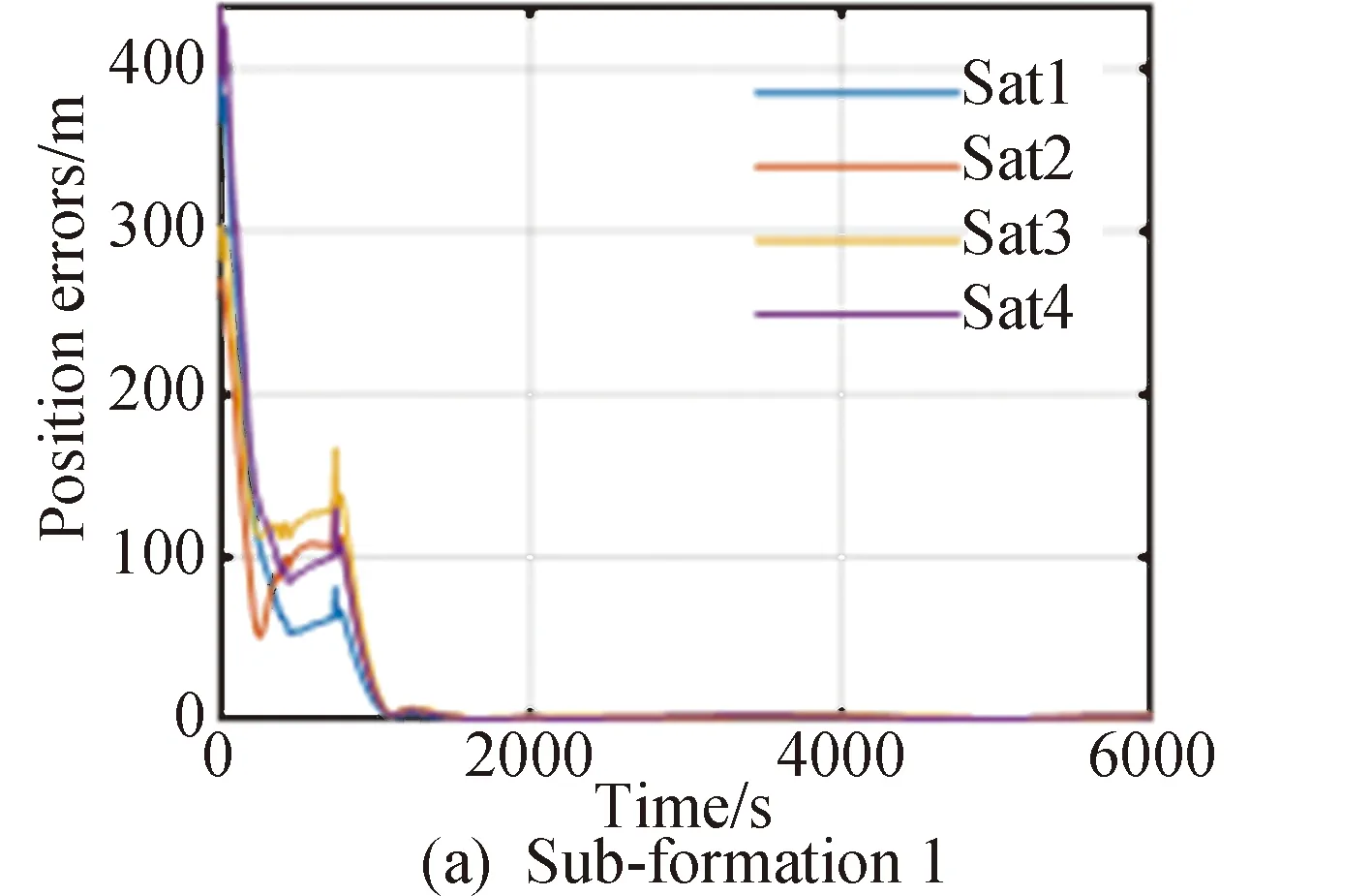
图5 各子编队内各组网卫星位置误差

图6 内部正方形编队及虚拟中心位置误差

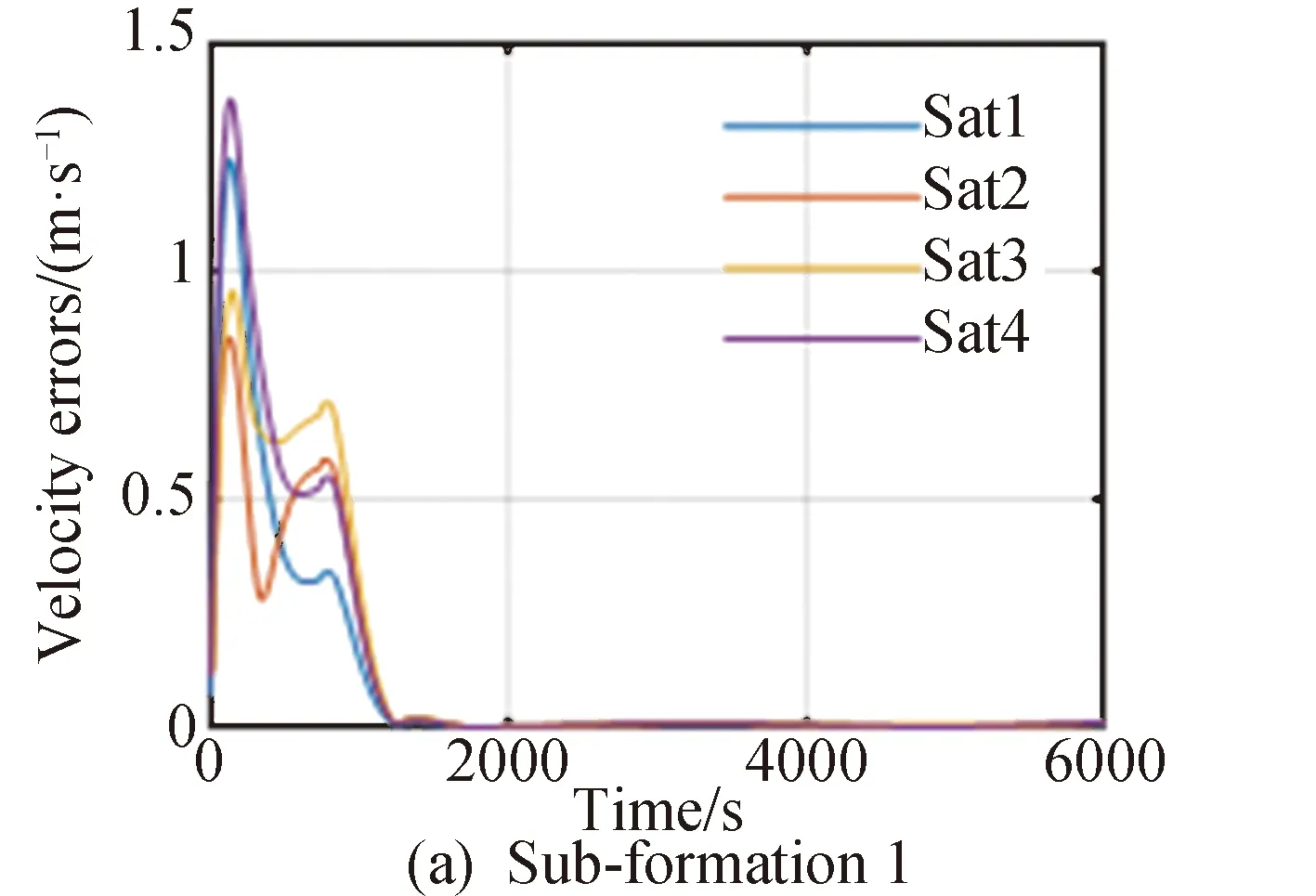
图7 子编队内各组网卫星速度误差

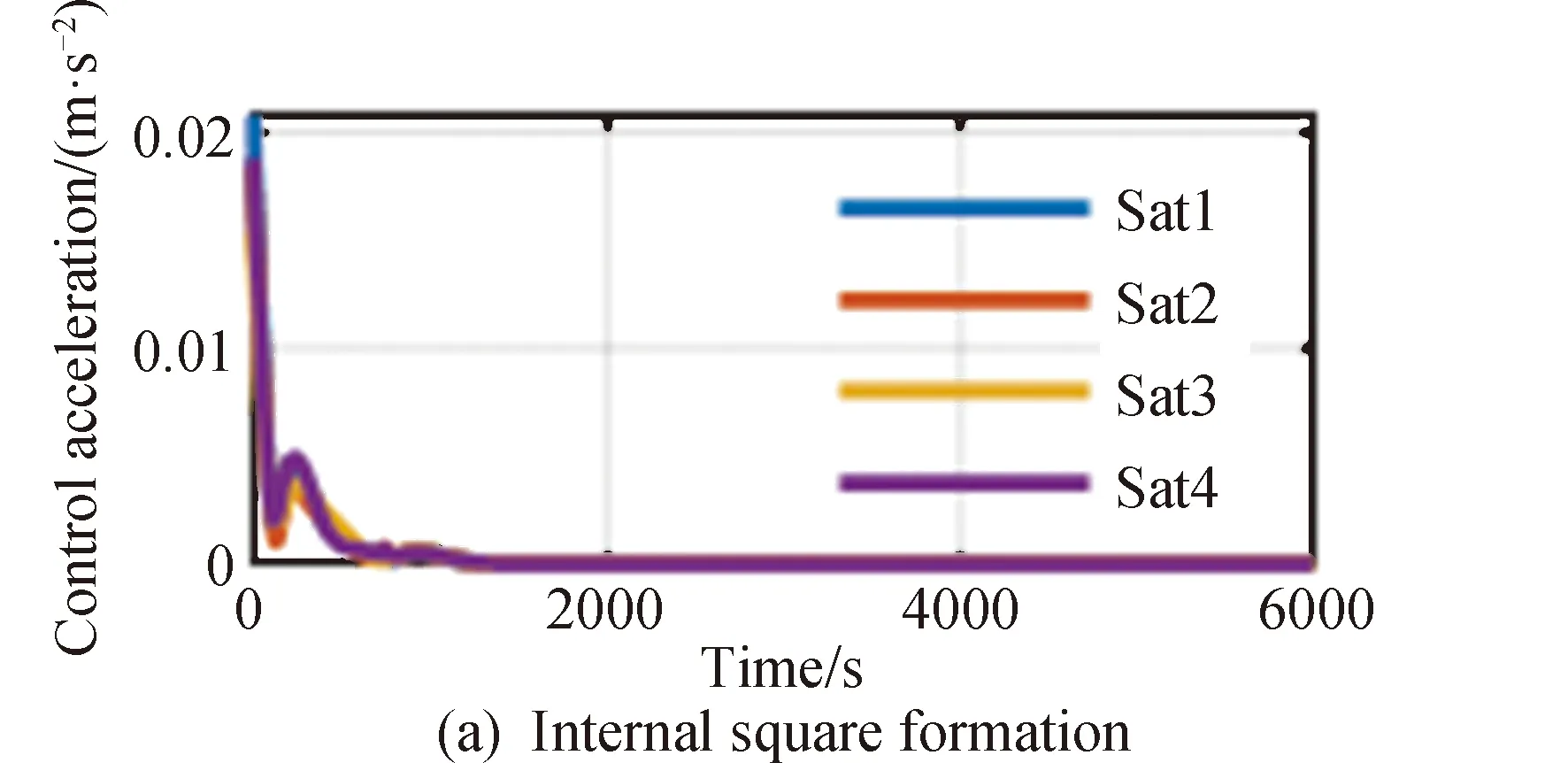
图9 各组网编队控制加速度

图10 超立方体组网拓扑结构编队相对运动三维图

在使用本文提出的ADDPG策略下,编队能够在1500s以内的时间完成高精度重构;在轨道保持阶段内部正方形编队位置误差可保持在0.3m以下,外围各子编队位置误差可保持在0.8m以下;内部正方形编队速度误差可保持在0.0015m/s以下,外围各子编队速度误差可保持在0.004m/s以下,能够较精确地完成控制任务。

将本文提出ADDPG算法和传统DDPG算法进行比较,结果如图11所示,图中红线表示基于DDPG算法得到的各编队以及虚拟中心的综合位置误差,蓝线表示基于ADDPG算法得到的各编队以及虚拟中心的综合位置误差。

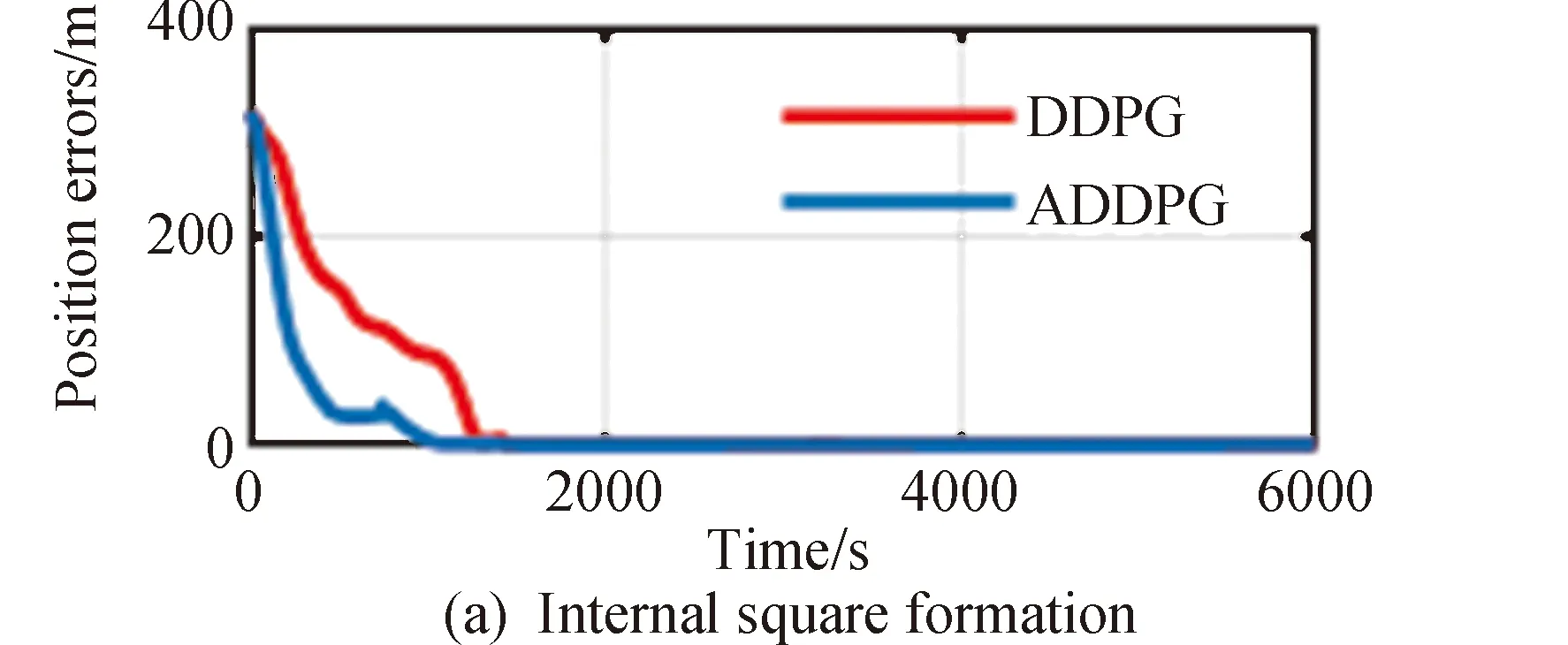
图11 DDPG和ADDPG对比

从图11可以清晰看到,ADDPG算法能较快地降低误差,ADDPG平均耗时1073s可达到收敛,DDPG算法平均耗时1271,使用ADDPG算法可以提高收敛速度14.79%。

同时,为进一步验证算法的有效性,采用本文方法和近两年在卫星编队方面国际上较权威的LMM[25]、RFFC[26]方法进行对比。为了公平方便地对比,相关主要参数与对应文献一致,结果如图12所示。

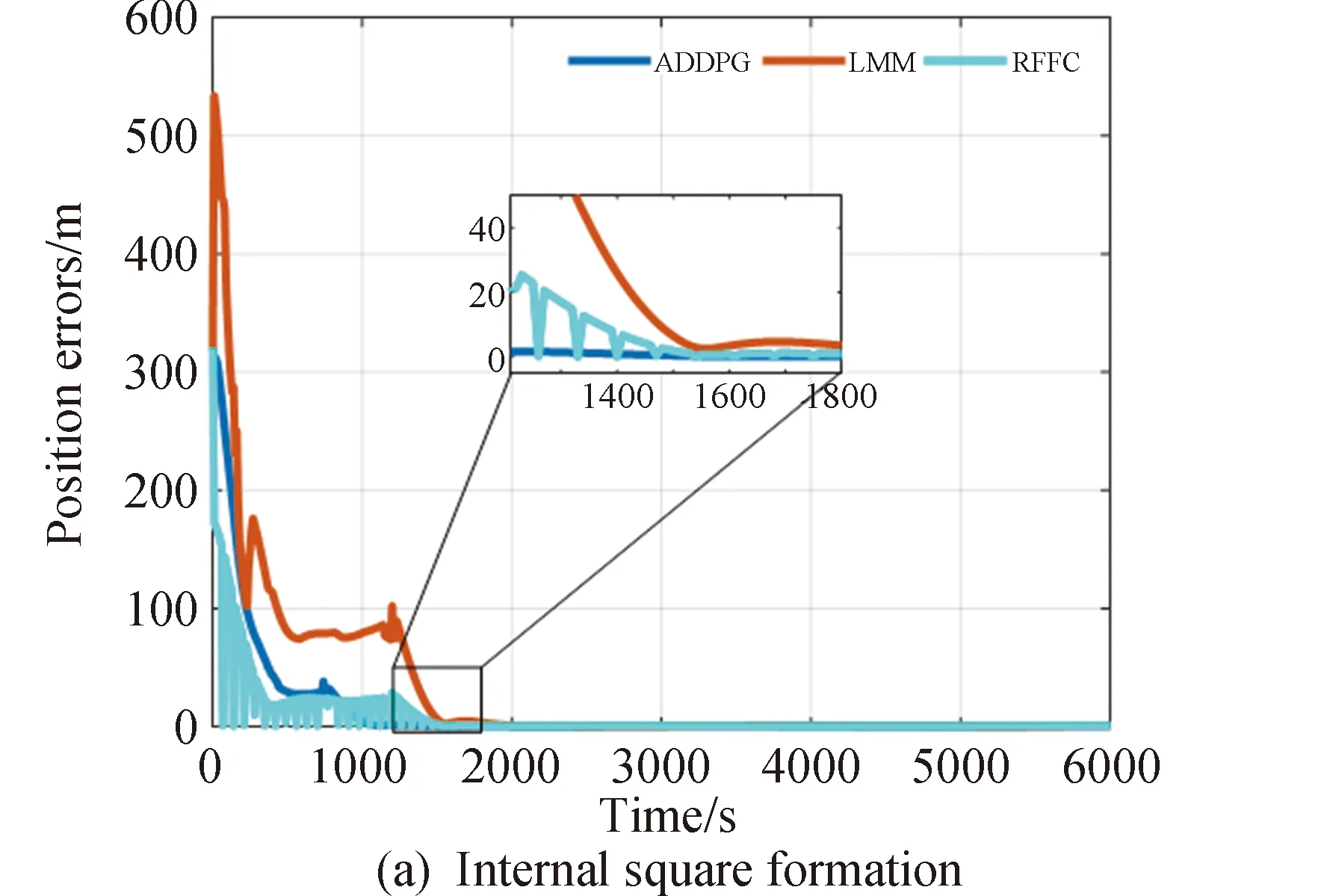
图12 误差对比

图12中蓝线、红线和青色曲线分别代表采用本文方法、 LMM方法、RFFC算法得到各编队以及虚拟中心误差。从图12可以看出,3种方法最终都能达到较高精度的稳定控制,其中ADDPG算法实现了最快收敛稳定,RFFC次之,LMM收敛较慢,RFFC虽然在子编队控制中较快达到了较高精度的比编队构型,但由于其设计的非线性控制器增强了对未知不确定性的估计控制,导致系统震荡较大,收敛时间较慢,但收敛后能达到较高的控制精度。

表2反映了3种策略条件下超立方体卫星编队内各卫星平均位置误差及卫星能耗对比。

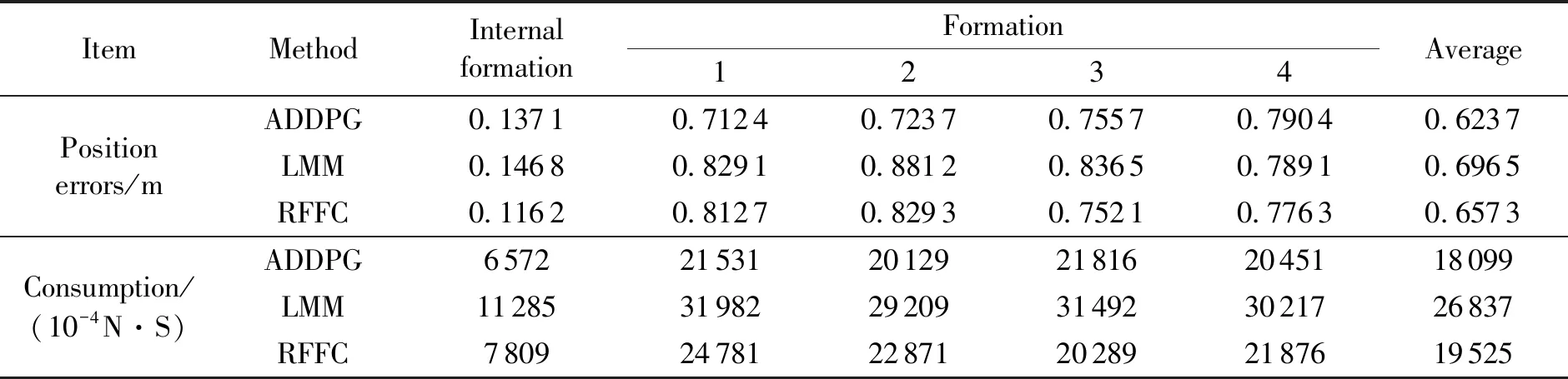
表2 超立方体卫星编队保持阶段仿真结果

由表2可以看出,采用基于ADDPG策略的卫星编队管理策略相比采用LMM方法、RFFC算法通过和环境交互学习,不断优化,平均误差相比LMM和RFFC分别减少10.43%,5.09%,同时采用ADDPG算法,能耗减少32.56%和7.3%,可实现在高精度编队位置保持的同时减少控制消耗,提高编队在轨寿命。

7 结论

本文针对大规模卫星编队控制,设计了基于ε-attraction动作选择的DDPG策略应用于卫星编队协同控制,主要结论如下:

1)超立方体拓扑结构对称、构型简单,良好的连通性和很强的扩展性适合大规模卫星编队系统组网设计。

2)通过建立编队动力学模型和超立方体拓扑图论理论,通过基于虚拟中心建立了编队整体漂移模型,有效实现了对卫星编队状态的衡量。

3)基于虚拟中心的奖励函数设计,既考虑了编队整体漂移控制,又考虑了各子编队卫星个体控制,将个体和整体进行协调控制,使算法规划出的编队综合代价最小。

4)基于ε-吸引策略在平衡算法探索和扩张的同时通过参考其他优异的编队卫星的状态信息和选择动作,降低学习模型初期探索过程中的盲目试错,提高了算法的收敛速度。以20星组网编队为例,仿真结果表明ADDPG策略可以用更低的能耗达到更高的精度,平均误差相比LMM和RFFC可以减少10.43%,5.09%,同时能耗可以减少32.56%和7.3%,算法在大规模卫星集群的智能控制发展方向上具有较大的应用前景。