改进小波包降噪与RSSD的滑动轴承声音诊断方法

汪思梦, 田中旭, 鲁洪江

(上海海洋大学 工程学院,上海 201306,E-mail:smWang1115@163.com)

滑动轴承结构简单、承载能力强,作为柴油机、内燃机等大型旋转机械中最重要的支撑部件[1],针对其进行监测,及时了解其运行状态和发现运行故障,对于保证滑动轴承的安全运行具有重要意义[2]。

目前,对于滑动轴承进行故障诊断主要基于振动信号[3]。文献[4]利用滑动轴承的振动信号,提出了基于EMD的全矢谱故障特征提取新方法。文献[5]提出了一种基于多重共振稀疏分解与多尺度符号动力学熵相结合的往复压缩机滑动轴承故障诊断方法成功实现滑动轴承的故障诊断。然而一些含滑动轴承的大型机械设备一般处在高速旋转以及高温、高压等复杂工作环境下,加速度传感器等接触式传感器的不易安装[6],利用振动信号对滑动轴承进行故障诊断受到限制。近年来,很多学者开始利用声音信号进行机械运行状态监测[7]。采集声音信号的传感器安装不受环境限制,不仅可以获取与振动相关的信息,还可以获取设备更多的状态信息。文献[8]提出一种基于改进形态-小波阈值降噪的轴承复合故障诊断声音诊断方法,即对采集到的故障轴承声音信号进行降噪处理,最终提取出了轴承故障特征频率。文献[9]利用改进的局域均值分解方法,分离声音信号中的不同成分,滤除了多个振源信号的噪声干扰,实现了齿轮箱故障监测。文献[10]利用速度波动的电机轴承,通过对原始瞬态声音信号的角度重新采样,实现了变速电机轴承故障诊断。

本文将声音信号应用于滑动轴承故障诊断当中,但基于声音信号的设备故障诊断目前存在很多仍需解决的问题,其中最主要的是噪声干扰问题[11]。首先,传声器采集到的信号除旋转部件旋转产生的声音信号之外,还包括设备其他部件例如电机等产生的噪声,相较于振动信号受到噪声干扰更加严重;同时声音信号传递到传声器的过程中在空气中会有所衰减,信号特征更加微弱,造成传声器中采集到的信号成分十分复杂,给研究带来了很大的难度。此外,滑动轴承还存在润滑状况和摩擦磨损等特征在声音信号中体现非常不明显的问题,导致利用声音信号进行滑动轴承故障诊断研究难度大、研究少。

针对上述问题,提出改进小波包降噪和共振稀疏分解(RSSD)的滑动轴承声音诊断方法,降低滑动轴承故障声音信号中的噪声干扰,分离故障特征信号,提取故障特征频率。

1 改进小波包降噪与RSSD的滑动轴承声音诊断方法

1.1 改进小波包降噪

滑动轴承在运转时,其声音信号显示出非线性非平稳的特点,且故障特征在声音信号中体现不明显,受到严重的噪声干扰。因此,在进行滑动轴承故障诊断时需要有效抑制噪声干扰。

本文提出的改进小波包降噪方法主要包括两个部分:一是对小波包分解进行优化,二是对小波包降噪进行改进。

一般情况下,人为设定小波包降噪参数具有随机性。因此,在对声音信号进行小波包降噪处理之前需要研究小波基函数、分解层数对降噪效果的影响,利用网格搜索法筛选最佳参数组合对滑动轴承声音信号进行小波包分解。

传统阈值仅与信号长度相关,然而噪声成分多存在于高频部分,随着分解尺度的增加而减少,所以传统固定阈值会滤除有用成分[12]。因此针对不同的小波分解尺度,需要选择与分解尺度相适应的阈值。针对传统阈值计算并未考虑到小波包分解尺度的问题,提出一种与分解尺度相适应的阈值对滑动轴承声音信号进行小波包阈值降噪处理。

1.2 共振稀疏分解

当滑动轴承发生故障时,其声音信号中会产生大量冲击成分,因此滑动轴承故障诊断的关键在于提取故障特征信号。共振稀疏分解方法基于信号的共振属性,可以有效将信号中的不同成分进行分离。将共振稀疏分解方法应用于滑动轴承故障声音信号中有望从故障复合信号中分离出故障冲击信号。

▲图1 滑动轴承声音诊断方法流程图

共振稀疏分解[13-14]方法具体实现过程为:首先利用可调品质因子小波变换对信号进行双通道滤波,获得相应的小波基函数库,信号里的不同成分可以用小波基函数库稀疏表示;再利用形态分量分析建立目标函数,采用分裂增广拉格朗日搜索算法对目标函数进行迭代,计算出目标函数的最小值,得到目标函数最小值对应的高、低共振系数以及对应的高、低共振分量,实现信号中不同成分的分离。

本文提出改进小波包降噪与RSSD的滑动轴承声音诊断方法流程如图1所示,具体步骤如下。

(1) 采用网格搜索法筛选最佳参数组合对滑动轴承声音信号进行小波包分解;

(2) 由于噪声信号多存在于高频段,利用本文提出与分解尺度相适应的阈值对分解后的高频系数进行阈值量化处理;

(3) 利用小波包分解后的低频系数和经过阈值量化的高频系数进行信号的重构,达到声音信号降噪的目的;

(4) 对降噪后的滑动轴承声音信号进行共振稀疏分解,分离出声音信号中的故障特征信号,即低共振分量;

(5) 对低共振分量进行包络分析,提取出故障特征频率。

2 信号采集

实验采用DHRMT-1转子实验台,转子实验台(图2),实验台由转子控制器、电机、光电测速仪、两个滑动轴承和两个平衡盘构成。两个电容式传声器灵敏度分别为47.31 mv/Pa和44.66 mv/Pa。将两传声器分别安装在三角支架上,为有效采集滑动轴承声音信号,将两个传声器放置在靠近电机端和远离电机端的两滑动轴承前;两个传声器与滑动轴承之间的距离保持一致;为了避免声音反射干扰,将传声器与加速度传感器分别布置在转子两侧。声音信号的采集使用8通道阵列信号采集仪,采样频率为12 000 Hz,采样时间为0.5 s。远离电机端的滑动轴承声音信号和振动信号对比如图3、4所示。

从图3中可以看出,声音信号和振动信号都显示出非线性非平稳的特点,其中声音信号受到噪声干扰更加严重。从图4中可以看出,振动信号的频谱图按照基频呈现存出周期性的特性,声音信号的频谱图无规则,且频率特征几乎淹没在噪声当中。因此,利用声音信号对滑动轴承进行故障诊断有两个重要的步骤,首先需要对声音信号进行降噪处理,其次是从降噪后的声音信号中分离出故障信号,提取故障特征频率。

▲图2 实验台测点布置

▲图3 声音信号与振动信号对比

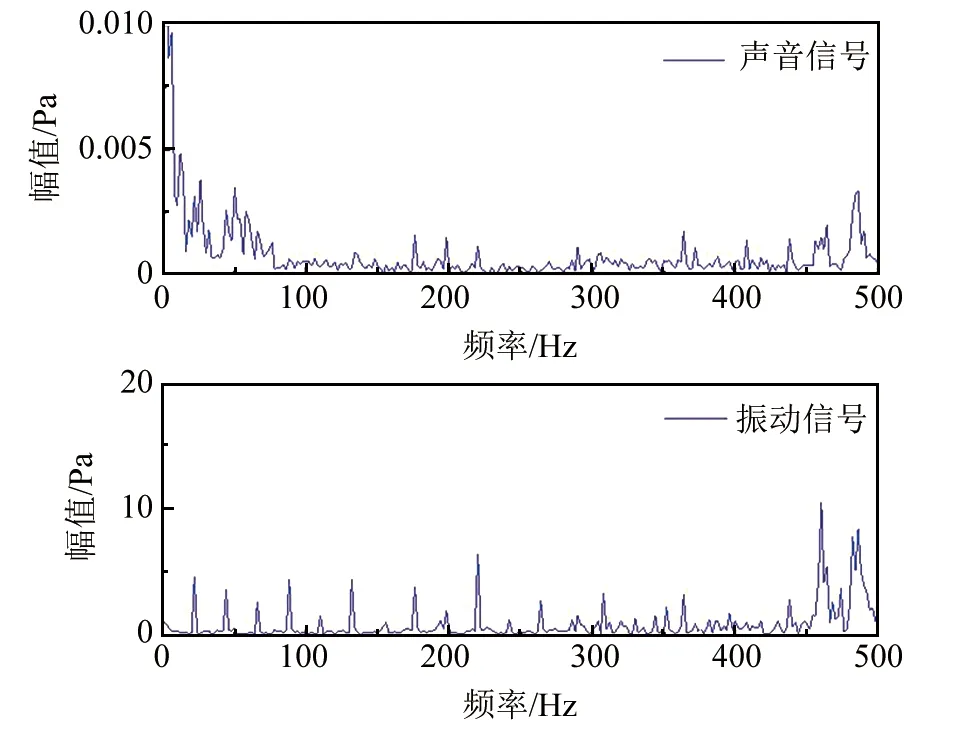
▲图4 声音信号与振动信号频谱对比

3 滑动轴承故障实验方法与分析

3.1 滑动轴承声音信号降噪实验分析

由于转子台控制器后的风扇转动产生大量噪声,靠近电机端的传声器采集到的声音信号受噪声干扰更加严重,因此选择此信号来研究各参数对降噪效果的影响规律。

本文以信噪比(SNR)和均方误差(MSE)作为评价小波包降噪效果的指标。在信号不发生畸变的情况下,信噪比越大,均方误差越小则说明降噪效果越好。

(1)

(2)

式中:x(n)为原始信号,y(n)为经过降噪处理后的信号,n为采样点的数目。

3.1.1 小波基函数对降噪的影响

选择常用的Sym、dB、Coif小波基函数,分别对声音信号进行小波包降噪处理。分解层数3层,“shannon”熵,阈值函数为软阈值,阈值类型选择“sqtwolog”阈值。结果如表1所示。

表1 小波基函数对信噪比和均方误差的影响

从表1中可以看出,Sym、dB、Coif小波基函数降噪后的信噪比随消失矩的增大而增大,均方误差随消失矩的增大而减小。

综合上述表格,经Coif5小波基函数降噪后,在保证信噪比较大的同时能保证较小的均方误差。因此,本文选择Coif5小波基函数。

3.1.2 分解层数对降噪的影响

选择Coif5小波基函数,通过改变分解层数,分析比较降噪效果。当分解层数较多时会导致信号畸变,分解层数较少会降低信号降噪效果,所以将分解层数聚焦在3～5之间。结果见图5。

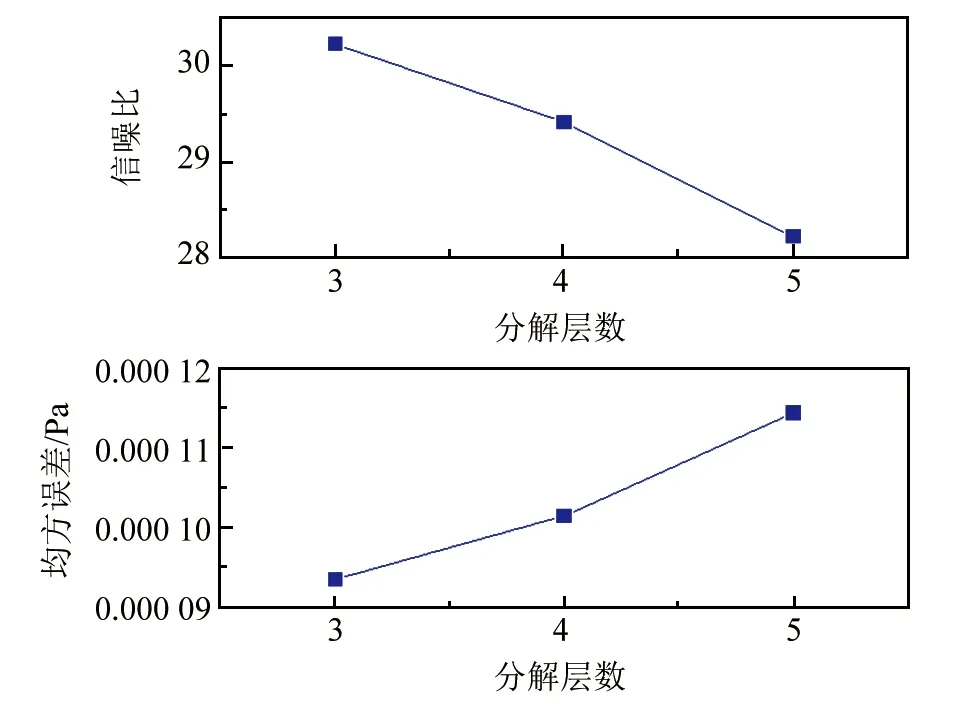
▲图5 分解层数的影响

从图5中可以看出,信噪比随着分解层数的增加而降低,均方误差均随着分解层数的增加而增加;当分解层数为3层时,信号的信噪比较大且均方误差都较小。因此,本文选择分解层数为3层。

3.1.3 阈值对降噪的影响

软阈值函数的定义为:

(3)

传统阈值λ计算公式为:

(4)

式中:σ为噪声标准差;N为信号长度。

(5)

median|wjk|为小波包分解第一层高频系数绝对值的中值,0.674 5为高斯噪声标准方差调整系数。

本文提出与分解尺度相适应的阈值,阈值设定为:

(6)

当j=1时,与式(5)计算结果相同,当j>1时,λj<λ,并随着j的增大而降低,符合噪声随小波变换的分布规律。

根据2.2和2.3节分析可知,最佳参数组合为Coif5小波基函数3层分解。对比传统阈值计算形式与本文提出与分解尺度相适应的阈值降噪后的声音信号信噪比与均方误差,结果如表2所示。

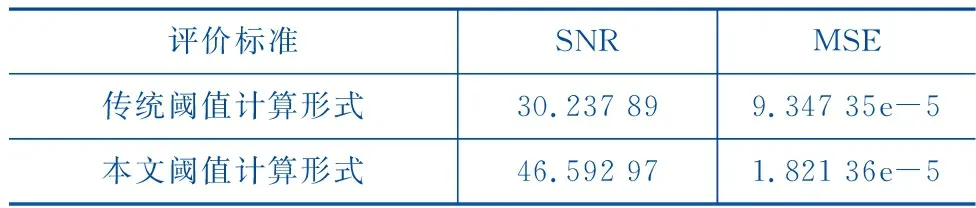
表2 本文阈值与传统算阈值降噪效果对比

经过计算,本文提出的阈值计算形式,在其余参数相同的情况下,将小波包降噪后声音信号的信噪比提高了54.09%,均方误差减小了80.51%。

3.1.4 对比传统小波包降噪

传统小波包降噪方法下的参数是人为设定的,为与本文提出的小波包降噪方法进行对比,随机选择sym4小波基函数4层分解、rigrsure无偏似然估计阈值类型。实验采集了转子实验台四种不同转速下滑动轴承的声音信号,两种方法降噪处理结果如表3所示。

表3 不同工况下本文降噪方法与传统降噪方法降噪效果对比

从表3中可以看出,对不同工况下的转子实验台滑动轴承声音信号进行降噪处理,利用本文改进的小波包降噪方法进行降噪处理后的不同工况下的滑动轴承声音信号的信噪比相较于传统方法下的滑动轴承声音信号信噪比大大提高,同时均方误差大大降低,证明本文的改进小波包降噪方法降噪效果显著。

3.2 分离滑动轴承故障信号实验分析

为模拟滑动轴承松动故障,卸除了实验台远离电机端的滑动轴承中的橡胶垫圈。滑动轴承正常运转和故障状态下的时域图如图6所示。

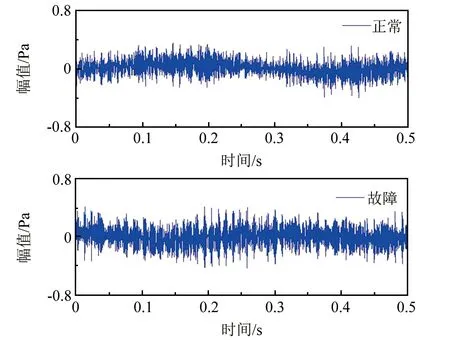
▲图6 滑动轴承正常运转和故障状态下的时域图

从图6中可以看出,当滑动轴承发生故障时,声音信号的振幅明显增大,且由于卸除了滑动轴承中的橡胶垫圈导致间隙过大产生了大量冲击成分。因此,冲击信号是分析提取轴承故障特征的目标信号。

共振稀疏分解算法可以依据信号中各种成分品质因子的不同,实现信号中不同成分的分离,有效分离出信号中的冲击成分,提高信号的冲击特性。本文选择高品质因子Q1=9、低品质因子Q2=3,冗余因子r=3。

首先对滑动轴承故障声音进行改进小波包降噪处理,结果如图7所示。

从图7中可以看出,经过改进小波包降噪方法降噪后的滑动轴承故障声音信号滤除了一部分噪声,同时较好的保留了信号原始的峰值和趋势。

对经过改进小波包方法降噪后的信号进行共振稀疏分解结果如图8所示。

从图8中可以看出,分离出的低共振分量中冲击特征明显,是滑动轴承故障特征信号。但时域图上无法观察不出频率信息,因此对分解后的低共振分量进行包络分析,结果如图9所示。

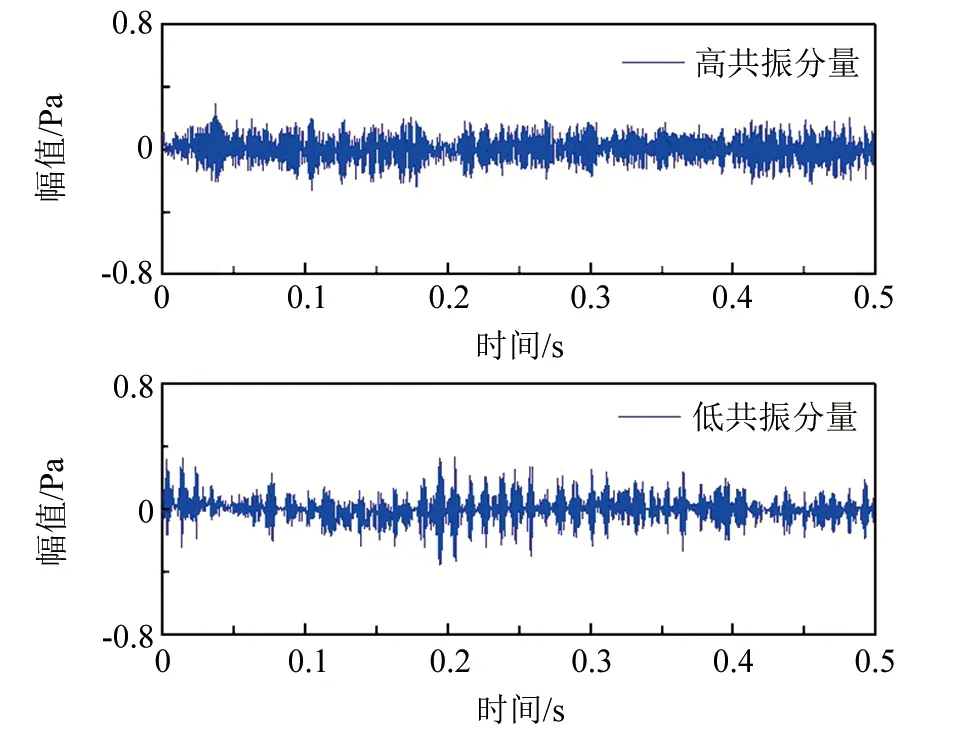
▲图8 共振稀疏分解结果图

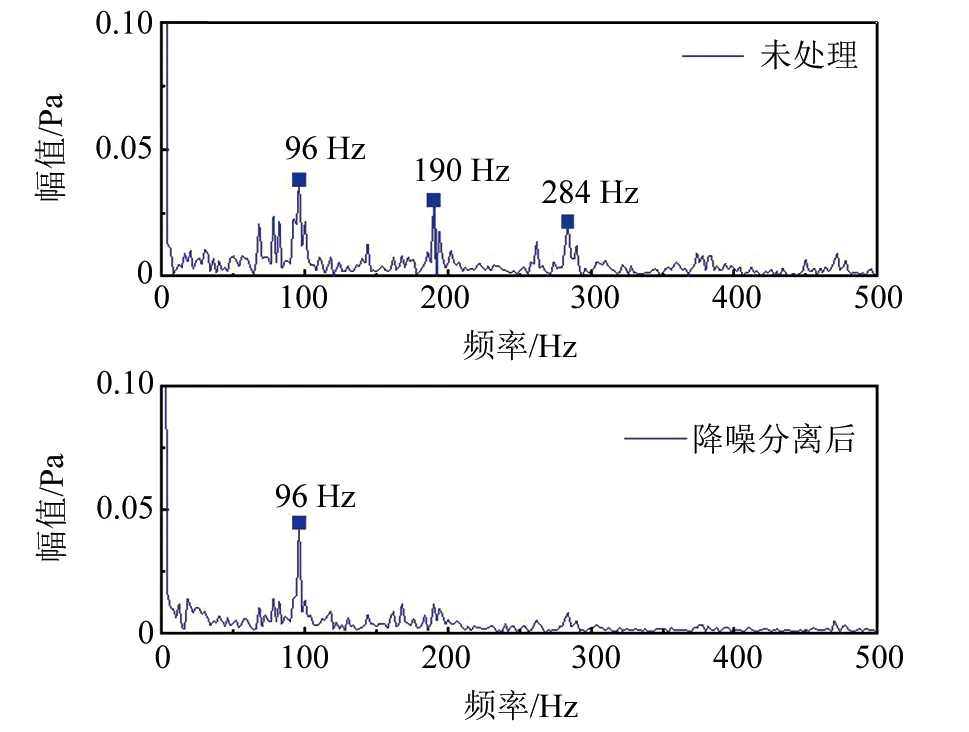
▲图9 故障声音信号的包络谱对比图

从图9中可以看出,未经降噪分离处理的原始滑动轴承声音信号故障特征频率淹没在噪声与干扰当中,无法利用包络谱准确判断滑动轴承的故障频率;然而经过改进小波包降噪处理以及共振稀疏分解分离后的声音信号的包络谱可以明显看到96 Hz的频率存在显著的谱线,这是由于间隙过大产生的冲击频率,说明本文方法成功分离出了信号中的冲击成分,提取出了滑动轴承声音信号中的故障特征频率为96 Hz。

4 总结

本文以含滑动轴承的转子实验台为实验对象,改进了小波包降噪方法,有效抑制了滑动轴承声音信号中的噪声干扰,应用共振稀疏分解方法分离并提取出了滑动轴承故障特征信号和故障特征频率,实现了利用声音信号进行滑动轴承故障诊断。经过研究,总结如下:

(1) 以信噪比和均方误差为标准,研究了小波基函数、分解层数对降噪效果的影响规律。Sym、dB、Coif小波基函数降噪后的信噪比随消失矩的增大而增大,均方误差随消失矩的增大而减小;信噪比随着分解层数的增加而降低,均方误差均随着分解层数的增加而增加。

(2) 利用网格搜索法筛选出最佳参数组合为Coif5小波基函数3层分解时,小波包分解效果最佳。

(3) 提出了与分解尺度相适应的阈值,通过计算分析,相较于传统阈值计算形式降噪后信号的信噪比提高了54.09%,均方误差减小了80.51%,具有更优的降噪效果。

(4) 应用共振稀疏分解算法成功分离出滑动轴承故障声音信号中的冲击成分,包络分析显示故障特征频率96 Hz谱线突出。

(5) 改进小波包降噪与RSSD的滑动轴承声音诊断方法去噪效果显著,能够有效提高信噪比,解决滑动轴承声音信号的噪声干扰问题,成功分离滑动轴承发生故障特征信号,提取故障特征频率。

(6) 本文方法为滑动轴承故障诊断提供了新的思路,具有工程应用价值。