气浮重力补偿装置变论域模糊控制策略设计

周 鑫, 赵 勇

(上海交通大学 上海市复杂薄板结构数字化制造重点实验室,上海 200240, E-mail:zhaoyong@sjtu.edu.cn)

卫星太阳能帆板作为卫星的重要能源装置,它的顺利展开是卫星能在太空环境下正常工作的前提。因此在发射卫星之前,需要在地面环境上进行多次的太阳能帆板微重力展开实验。气浮重力补偿装置是用气浮法实现重力补偿的关键部件,对气浮重力补偿装置的控制效果直接影响太阳能帆板地面展开实验的实验效果[1]。

由于受到地面不平度和气膜自身振动的干扰,对气浮重力补偿装置的控制难度较大。普通的模糊PID控制策略由于其论域范围固定不变,对PID控制参数调整不当,控制精度和稳定性下降,难以满足帆板在地面环境中进行展开实验的控制性能要求。

自李洪兴提出变论域模糊控制方法以来,变论域控制思想得到了广泛的应用[2]。近年来,国内外学者对变论域模糊控制方法进行了深入研究。文献[3]提出一种基于变论域模糊PID的串级控制算法来解决四旋翼无人机系统存在的控制精度差和鲁棒性低的问题。文献[4]为提高汽车乘坐的舒适性和行驶的平顺性,提出一种基于变论域理论的自适应模糊PID汽车主动悬架控制策略。文献[5]将叉车的侧倾状况进行分析,采用变论域模糊控制方法设计控制器,仿真与实验结果表明该策略可有效提高叉车的横向稳定性。文献[6]对于导弹的飞行控制,设计了一种自适应变论域模糊PID复合控制策略,实验结果表明该方法具有抗干扰性强,响应速度快的特点。国内外学者主要采用普通PID或模糊控制策略来整定传统的气浮轴承式重力补偿装置的控制参数[7-10],对于悬浮气垫式重力补偿装置以及变论域模糊控制策略研究较少。

由于变论域模糊控制具有不依赖被控对象精确数学模型的优点,结合气浮装置本身的非线性,难以建立准确数学模型的特点,本文根据气浮重力补偿装置主要组件的分析建立了装置的控制模型,分析了地面不同工况干扰以及气膜自身振动干扰对支撑点位置的影响,并结合帆板展开过程的动力学模型提出了一种适用于气垫悬浮式重力补偿装置的变论域模糊PID控制策略,最后在仿真模型中设计了四组不同的仿真实验并搭建气浮实验台以验证所提控制策略的适用性和可靠性。

1 气浮重力补偿装置分析

1.1 重力补偿装置控制模型

▲图2 装置等效结构原理图

气浮重力补偿装置是用气浮法实现帆板重力补偿的关键部件,它主要由补偿组件、微调组件和气垫组件组成,如图1所示。

补偿组件为电动缸,在电动缸丝杠末端安装位置传感器用于回传支撑点实时位置信息,通过上位机可动态调整电动缸输出的补偿支撑力和伸出轴的长度。微调组件中包含三个碟簧、三个球铰和一个三角支撑盘,用于微调气浮重力补偿装置因地面工况变化而引起偏载的姿态。气垫组件包含气垫支撑盘和悬浮气垫,替换传统的气浮轴承,以适应平整度较差的地面工况。

气浮重力补偿装置的等效结构原理图如图2所示。

受力分析后可建立力平衡方程:

(1)

式中:m1为气垫支撑盘和气垫的等效质量和,k1为等效气膜刚度,c2为等效气膜阻尼,m2为微调机构与电缸的等效质量和,k2为其等效刚度,c2为其等效阻尼。xi为地面不平度等干扰因素引起的小位移扰动量,x为气垫相对于基准面的位移量,xo为微调机构相对于基准面的位移量。

将以上方程联立,进行拉普拉斯变换并整理后得到:

(2)

式中:参数如下:

参考文献[3],电动缸电机的传递函数为:

(3)

式中:Kf为位置传感器增益,T为时延系数。由此可得到气浮重力补偿装置在竖直方向位置传递函数模型:

(4)

当电动缸末端的位置传感器检测到位置误差时,上位机会调用预先设计的自适应位控算法动态调整伸出杆的伸出长度,从而补偿支撑点的位置误差,维持帆板在地面展开过程中的平稳性。

1.2 气膜振动与地面扰动工况分析

气浮重力补偿装置实现气浮效果的关键组件是悬浮气垫,悬浮气垫通过高压气源输入的压缩空气给气垫充气,气垫底部的节流孔溢出气体形成气膜,由气膜的气浮力平衡其支撑物体的重力,悬浮气垫的工作原理图如图3所示。

▲图3 悬浮气垫工作原理图

假设当气垫的承载为G时,气膜的厚度为h,当气压稳定时,悬浮气垫的承载力和气膜的厚度呈反比关系[11],即:

(5)

式中:k为影响系数。气垫在地面移动的过程中,由于有高压气流和橡胶气囊的弹性变形的作用,气膜会出现振动的现象,形成了支撑点位控干扰工况。设气垫在地面移动过程中的实际气膜厚度为h,则有:

h=h0+Δh

(6)

式中:h0为气膜稳定厚度,Δh为气膜的瞬时变化量。借鉴文献[12]里面的振动模型,悬浮气垫的振动以简谐振动的方式建模,即:

Δh=A·sin(ωt)=εh0·sin(ωt)

(7)

式中:ω为简谐振动的固有频率,rad/s,取2πf;f为扰动振源的频率,Hz;ε为扰动因子;t为时间,s;A为小位移扰动的扰动幅值,mm。

气膜的厚度除了与气膜自身振动相关外,还与气体的粘度,气垫弹性模量以及地面粗糙度等因素相关,用H表示气垫表面和地面之间的广义气膜厚度,则:

H=h+δ=h0+Δh+δ=h0[1+ε·sin(ωt)]+δ

(8)

其中:δ为考虑了地面不平度等外界扰动的微调量。

气垫在地面移动过程中会碰到一些典型的地面工况,如随机不平地面工况,斜坡地面工况以及斜坡凹凸地面工况等,如图4所示。

▲图4 典型地面工况示意图

▲图5 气垫斜坡力变干扰示意图

对于斜坡地面工况,悬浮气垫由平地面上升到斜坡过程中,气垫与地面之间的气膜厚度会发生突变,垂直于气垫支撑盘竖直方向上的气垫承载力也会产生力变,由图5可知力变大小为:

ΔG=G(1-cosα)

(9)

式中:α为斜坡倾角,由于有微调机构的存在,气浮重力补偿装置能在斜坡位置上处于新的平衡状态,从而保持帆板在展开过程中的水平度, 由于气膜厚度和气垫的承载力相互影响,当气垫承载从G0变化到G0-ΔG时,气膜厚度会从h0变化到h0+Δh,可将该过程视为阶跃突变干扰,干扰幅值为:

Δh=cosδk/G0-k/G0

(10)

气垫从斜坡地面移动到平地面是其逆过程,分析同理。

对于随机不平的地面工况,许多国内外的科研机构对路面不平度的数据测量和分析表明,路面不平度难以用明确的数学表达式表征,但可用以时间为参数的随机过程表示。当车速较低时,其路面轮廓表面高程服从零均值的稳态高斯概率分布。由长春汽车研究所起草制订的 GB/T7031-1986《车辆振动输入-路面不平度表示方法标准 》中用功率谱密度函数系数的几何平均值和均方根值将路面划分为ABCDEFGH共8级[13]。2个参数的数值越小表示路况越好,路面等级越高,如表1所示。

表1 路面不平度8级分类标准

由于悬浮气垫对实验地面具有一定要求,在裂缝,高粗糙度的地面环境下无法形成稳定气膜,要求实验地面整体上平整光滑,因此可将普通的实验室地面工况视为A级路面工况。后续扰动参数的设置可依据此表作为参照。

由于帆板在地面展开实验测试中需要进行大范围的展开运动,因此需建立帆板地面展开过程的动力学模型,结合其动力学特性设计控制策略。

1.3 帆板展开动力学建模

卫星太阳能帆板之间通过铰链连接,由于帆板表面的太阳能薄膜的刚度较小,重量较轻,因此将帆板简化为铝合金型材框架进行分析。图6表示柔性帆板多体系统中的一块帆板。

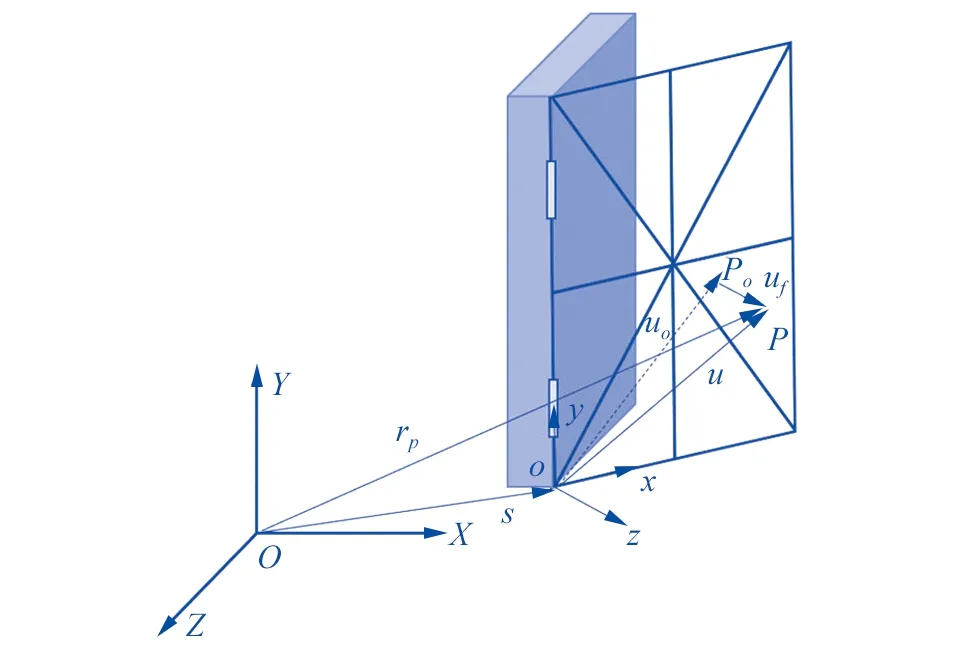
▲图6 帆板上任意点的变形描述

设O-XYZ为固定在基准面上的惯性坐标系,o-xyz为固定在柔性帆板上的浮动坐标系,选取帆板上任意一点P为研究点,则该点在惯性坐标系下的位置矢量可以表示为:

rp=s+A(uo+uf)

(11)

式中:s表示浮动坐标系原点在惯性坐标系中的位置矢量,uo表示任意点P在帆板未变形的情况下在浮动坐标系下的位置矢量;uf表示帆板变形的位移量,A表示从浮动坐标系到惯性坐标系的旋转变换矩阵。

根据假设模态法,帆板上任一点的变形量可以由一组模态函数和模态坐标的线性组合来表示[14],即:

uf=φξ

(12)

代入式(11)得:

rp=s+A(u0+φξ)

(13)

对上式求一阶导数得:

(14)

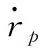
(15)

用模态坐标表示帆板的弹性势能V和耗散能D:

(16)

式中:C为广义模态阻尼矩阵,K为广义模态刚度矩阵,{ξ}为模态坐标列阵。

将动能、势能以及作用力代入拉格朗日方程中

(17)

整理得到矩阵形式的动力学方程

(18)

2 变论域模糊PID控制器设计

2.1 模糊PID控制器设计

(1) 变量模糊化

模糊控制器采用两输入三输出的形式,2个输入变量为支撑点位置误差e和位置误差的变化率ec, 3个输出变量为PID控制器三个修正量ΔKP、ΔKI、ΔKD。

设e和ec的实际量的最大值分别为emax,ecmax,则它们基本论域的取值范围可分别表示为[-emax,emax], [-ecmax,ecmax]。通过量化因子Ke与Kec可将e和ec的实际量映射为模糊论域的模糊量[15]。由于本文对模糊控制器的实时性和计算精度具有较高要求,因此将输入输出变量模糊论域划共划分为7个模糊子集{NB,NM,NS,ZO,PS,PM,PB},且模糊论域均设为[-3,3],则Ke=3/emax,Kec=3/ecmax。选择常用的三角型隶属度函数作为每个模糊子集的隶属度函数,因为其形状简单,占用空间小,适合控制器在线调整,能实现较快的响应速度[16]。三角型隶属度函数如图7所示。

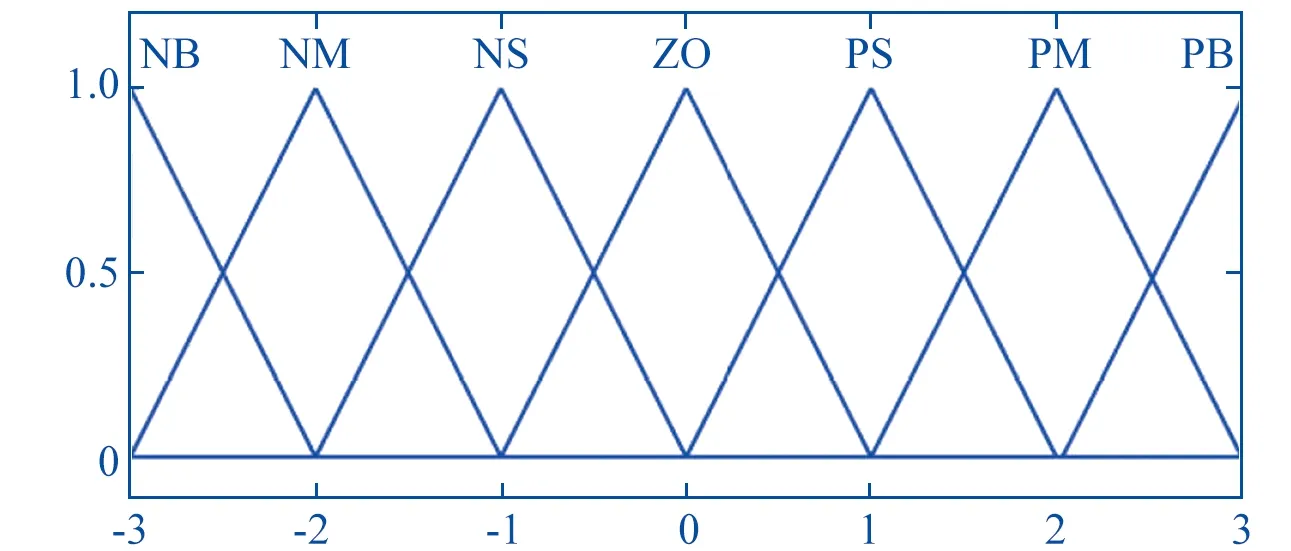
▲图7 隶属度函数

(2) 模糊规则表设计

将输入输出变量模糊化之后,接下来就要设计模糊规则表,模糊规则表的设计对于模糊PID控制器的控制效果有着关键的影响,根据PID参数的整定原则,参照专家对气浮装置的控制经验[17],总结出ΔKP、ΔKI、ΔKD模糊控制规则表, 以ΔKP为例,如表2所示。

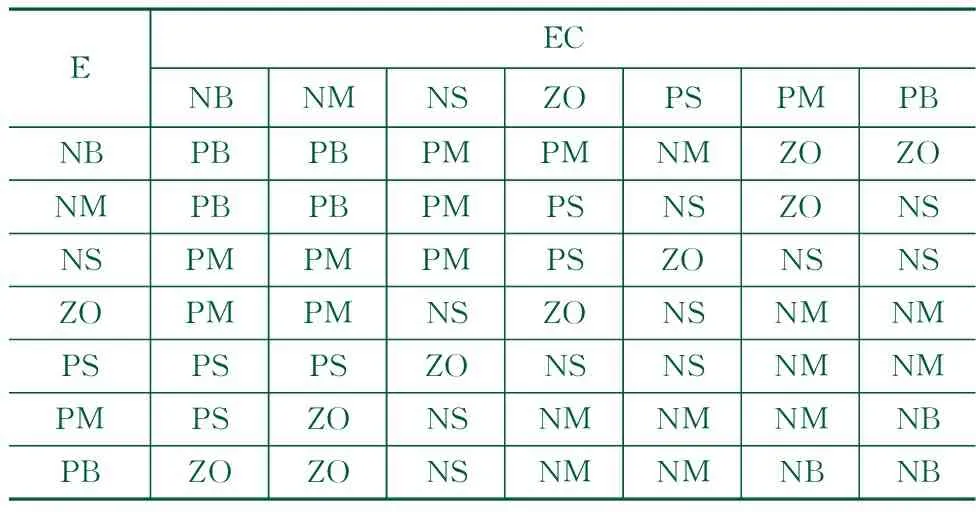
表2 ΔKP模糊规则表

(3) 模糊推理与解模糊

模糊推理采用Mamdani的min-max法,模糊推理的输出量为3个输出变量的模糊值,最后还需用重心法解模糊,其公式为:

(19)

解模糊后便可得到3个输出变量的精确值,将PID参数的初始值加上修正值,便可得到最终纠正后的PID整定参数。即:

KP=KP0+ΔKP
KI=KI0+ΔKI
KD=KD0+ΔKD

(20)

式中:KP,KI,KD为纠正后的PID参数值, 则模糊PID控制器的系统离散形式输出量为:

(21)

式中:k表示采样时间点。

2.2 变论域伸缩因子设计

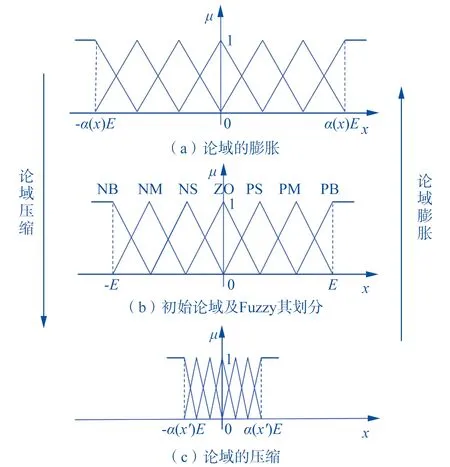
模糊PID控制器虽然能取得基本可行的控制效果,为了进一步提高系统的控制精度,可将模糊论域细分,即增加模糊子集的个数,但该方法会导致模糊规则冗余,利用率较低,且降低了控制系统的实时性。模糊PID控制器的另一个缺陷是其模糊论域以及量化因子,比例因子均为常数,一旦设定好就不可更改,在实际控制过程中会出现响应速度变慢,自适应变差的现象,鉴于以上问题,文献[2]首次提出变论域思想,将变论域模糊控制器视为一种动态逐点收敛的分片插值器,在普通模糊PID控制器的基础上引入了伸缩因子的概念。伸缩因子是一个论域自调整模块,将伸缩因子和模糊论域的边界值相乘可动态地调整模糊论域的范围,当误差变大时,模糊论域范围扩张,当误差变小时,模糊论域范围收缩。变论域控制原理图如图8所示。变论域模糊控制器在不改变原有模糊规则和隶属度函数形状的前提下能相对增加在误差零点位置附近的控制规则的数量,提高了模糊规则的利用率,因此其控制精度更高。变论域模糊PID控制器的结构图如图9所示。

▲图8 变论域原理图

▲图9 变论域模糊PID控制框图

设两个输入变量误差e和误差的变化率ec的初始论域为[-E,E], 引入输入伸缩因子α(x)后得到变论域为[-α(x)E,α(x)E], 同理,设三个输出变量的初始论域为[-U,U],引入输出伸缩因子β(y)后得到变论域[-β(y)U,β(y)U]。为简化在线计算时的复杂度,提高控制系统的实时性,对于输入伸缩因子,本文选择函数型伸缩因子,常见函数型伸缩因子的形式有比例型和指数型两种:

(22)

式中:0<τ<1,ε为充分小的趋近于零的正数。

α(x)=1-λexp(-kx2)

(23)

式中:0<λ<1,k>0。

在系统动态调整的过程中,函数型伸缩因子因含有常量参数,当被控对象变化时,需要设定不同的常量参数,缺乏通用的选择函数中常量参数的方法[18]。为此,本文根据系统中误差和误差的变化率来实时调整指数型伸缩因子中的λ和k参数,并根据文献[2]中对伸缩因子的性质要求提出一种新型函数型伸缩因子:

(24)

式中:e和ec分别表示实时误差和实时误差变化率,E和EC分别表示误差和误差变化率的初始论域边界,ε为一个趋于0的足够小的正数。

对于输出伸缩因子,结合其单调性原则以及PID参数的各自的整定作用,比例环节ΔKP和微分环节ΔKD的单调性应和位置误差保持相同,积分环节ΔKI的单调性应和位置误差保持相反。则设计的输出伸缩因子为:

(25)

由于模糊控制器的本质是插值器,其控制输出量可表示为:

(26)

其中:xi为输入变量,yj为插值输出值,Aij为模糊划分。引入了伸缩因子后,变论域模糊控制器输出量可表示为:

(27)

至此完成了变论域模糊PID控制器的设计,通过伸缩因子的调节作用,减少了对专家经验的依赖,提高了模糊规则的利用率,因此增强了系统的容错性和自适应性。

3 仿真与实验验证

3.1 仿真分析

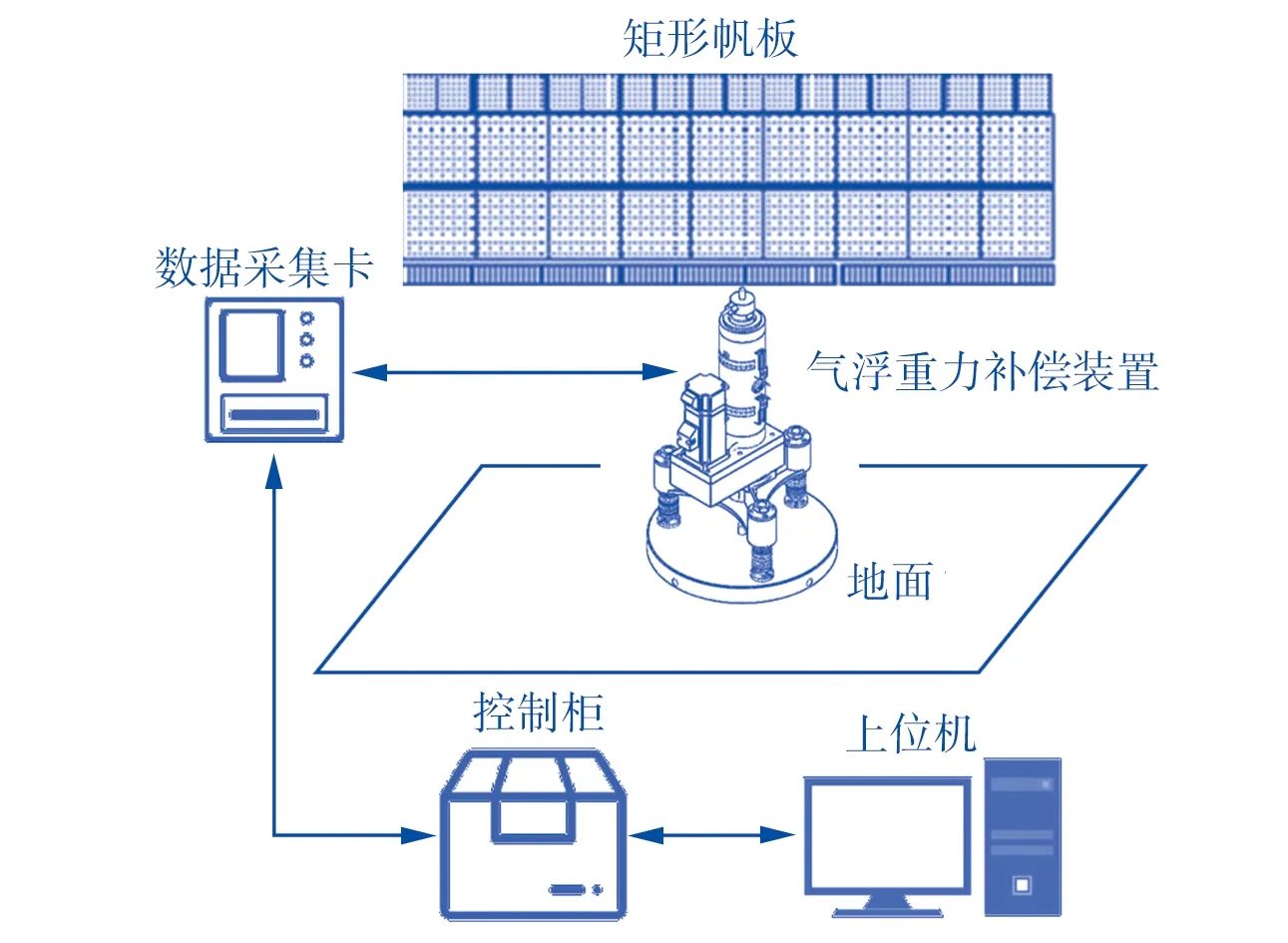
在帆板地面展开实验环境中,气浮重力补偿装置上方支撑帆板补偿其重力,下方通过悬浮气垫底部溢出的高压气流形成气浮力悬浮于地面之上,装置的实验环境如图10所示。

为验证本文提出的变论域模糊PID控制策略对气浮重力补偿装置的控制效果,依据上述实验环境并结合1.1节分析的控制模型,在Matlab/Simulink中搭建了控制仿真模型,采用阶跃信号模拟上位机设定的支撑点目标位置,将输入输出伸缩因子以函数模块的方式嵌入模糊PID控制器中,变论域模糊PID控制模块如图11所示,总体的控制模型如图12所示。设支撑点的初始位置即控制器的输入目标位置为300 mm,该位置为达到气浮稳定状态位置,选择四种工况进行仿真实验:阶跃扰动,随机扰动,正弦随机混合扰动与阶跃正弦随机混合扰动。具体实施过程如下:

▲图10 帆板展开测试实验环境示意图

仿真实验1:为验证变论域模糊PID控制器在地面环境干扰下的自适应能力,在3 s处施加一个2 mm的阶跃扰动信号模拟地面微小凸起工况,从图13以看出,变论域模糊PID控制器受到外部扰动后,最大误差约为0.6 mm,恢复平稳的时间约为0.8 s, 而普通模糊PID控制器的最大误差约为0.9 mm,且需要1.4 s左右的调节时间才趋于平稳,由此表明变论域模糊PID的调节速度快,动态响应性能较好,抗外部干扰能力强,对于地面微小凸起干扰的工况有一定的自适应能力。

▲图11 变论域模糊PID控制器

▲图12 系统总体控制框图

▲图13 阶跃扰动响应

仿真实验2:为模拟地面高低不平的随机性干扰,参考表1对路面不平度的8级分类标准中的均方根值参数,图14为在第3 s加入了均值为0 mm,方差为16 mm的高斯随机干扰信号后的仿真结果。由图14可知,引入随机干扰信号后,普通模糊PID控制响应曲线的最大位置误差有1.3 mm,而变论域模糊PID的控制最大误差仅有0.5 mm,误差率相对减少了约61%,说明相对于普通模糊PID控制,变论域模糊PID控制的控制精度和动态稳定性更高。

▲图14 随机扰动响应

仿真实验3:为模拟气膜振动和地面不平度的混合干扰工况,结合对气浮垫气膜振动工况的分析,在仿真实验2的基础上增加一个幅值A=2 mm,频率f=20 Hz的正弦扰动信号,如图15所示,变论域模糊PID的控制响应曲线的最大误差约为0.5 mm,而普通模糊PID的最大误差有1.5 mm, 变论域模糊PID相较于普通模糊PID的误差波动范围更小,再次验证变论域模糊PID拥有较强的抗外部干扰能力。

▲图15 正弦与随机混合扰动响应

仿真实验4:在仿真实验3的基础上,在4 s处增加一个2 mm的阶跃扰动,并且将正弦扰动的频率值增大到50 Hz, 模拟气浮垫从平地面上升至斜坡凹凸地面的过程。从图16可以看出,在该混合扰动工况下,普通模糊PID和变论域模糊PID响应曲线均出现明显波动,但是总体而言,变论域模糊PID响应曲线位置误差波动范围更小,最大位置误差约为0.6 mm,而普通模糊PID响应曲线的最大位置误差达到了1.8 mm,表明在多种扰动源同时干扰的工况下,对气浮装置采用变论域模糊PID控制策略依然具备较强的动态稳定性和鲁棒性。

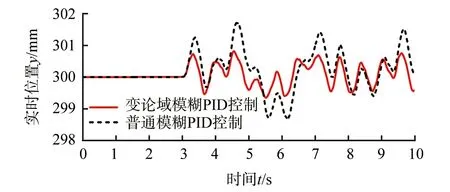
▲图16 阶跃正弦随机混合扰动响应

表3整理了上述四种仿真实验的仿真结果数据。

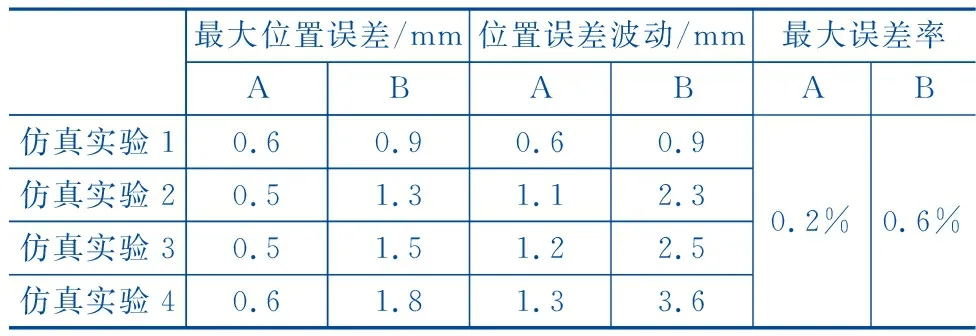
表3 仿真结果对比

表3中,A代表变论域模糊PID控制的仿真结果数据,B代表普通模糊PID控制的仿真结果数据。位置误差波动为正向最大误差与负向最大误差的绝对值之和,将最大误差绝对值除以目标值得到最大误差率。由表3可知,变论域模糊PID控制能将帆板展开过程中支撑点的位置误差率控制0.2%在以内,相对于普通模糊PID控制位置误差率减小了约66%,对于不同形式的扰动工况均表现出良好的稳态特性和控制精度。

3.2 实验验证

为验证变论域模糊PID控制策略的实际控制效果,搭建帆板展开气浮实验台进行单块帆板的微重力地面展开实验。气浮实验台主要由两块铝合金帆板框架,支架车,气浮重力补偿装置,控制箱以及上位机组成,如图17所示。

▲图17 气浮重力补偿实验平台

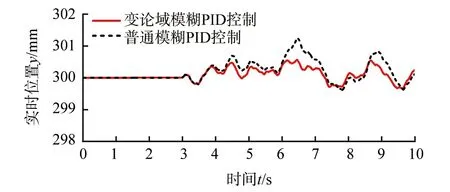
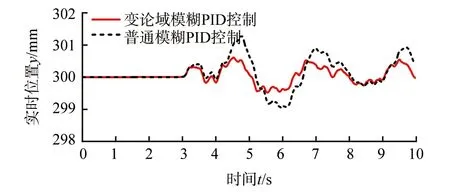
在实际物理实验中,经测量当气膜稳定时,气浮装置支撑点距离支撑架车水平面的垂直距离约为350 mm,故在上位机控制软件中设置目标位置为350 mm,启动内外侧2个支撑装置而后进行帆板地面微重力展开实验。结果如图18和图19所示。

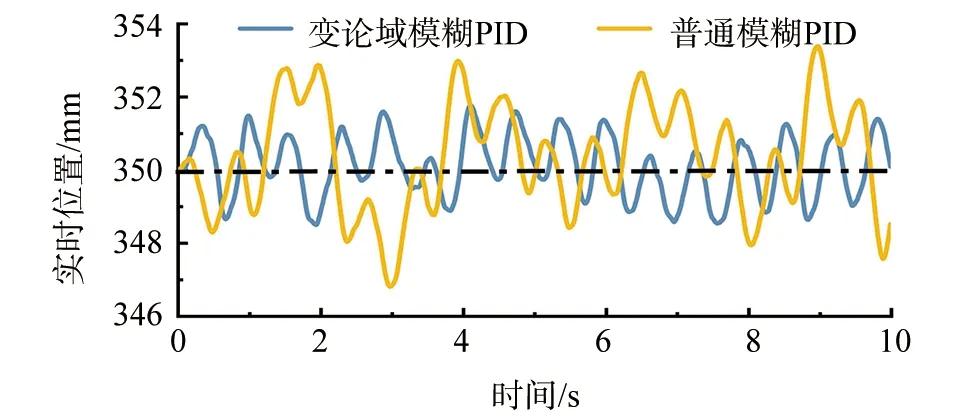
▲图18 内侧支撑点展开过程实时位置变化图

表4为帆板展开过程两支撑点位控结果对比。

表4 帆板展开过程两支撑点位控结果对比

由表4可知,在普通模糊PID控制策略作用下内外侧支撑点的最大位置误差率达到了1.2%,而在变论域模糊PID控制策略作用下,最大位置误差率可控制在0.6%以内,且位置波动范围更小。实验结果表明本文设计的一种带有新型函数型伸缩因子的变论域模糊PID控制策略相较于普通模糊PID控制策略的控制精度更高,抗干扰能力强,能自适应地面不平整的工况。

4 结论

本文对太阳能帆板地面展开实验中气浮重力补偿装置的控制问题进行了研究,建立了气浮重力补偿装置的控制模型,分析了气膜和地面的扰动工况,设计了一种适用于气浮重力补偿装置的变论域模糊PID控制器,提出了一种新型函数型伸缩因子,仿真与实验结果表明变论域模糊PID控制器能将支撑点位置误差控制在0.6%以内,相较于普通模糊PID控制,误差率减小了50%,动态调节速度快,稳定性好,抗干扰性强,对气浮重力补偿装置的控制取得了较好的控制效果。