无人自行车的负载特性研究与分析

黄用华, 唐心旭, 庄 未, 萧洪亮, 骆泽众, 张兴原

(桂林电子科技大学 机电工程学院,广西 桂林 541004,E-mail:huangyonghuaxj@sina.com)

无人自行车具有安全可靠、节能环保、结构简单、易于控制等特点,能够在地形较为狭窄处灵活穿梭,对运输行业的“最后一公里”问题提供了新思路;另外,无人自行车在避障、救援以及躲避交通拥堵等场景有独特优势,对城市交通救援拥堵问题提供了新方法。在交通、救援、服务等领域有广泛的应用前景。

古文生等人[1]为研究无人自行车静态平衡控制问题,以建立的动力学模型为基础,设计一种LQR算法,实现系统在车把转角为90°的条件下实现静止平衡。Cristina Budaciu等人[2]基于动力学方程使用经典PI控制器控制车轮转速以及使用LQR控制器控制车把转角的方法对其进行轨迹控制研究。西南大学的陈俊杰[3]设计了一种便携式手推与跨骑可变的两轮车,通过手动进行结构的变换。石丹妮[4]基于HD-算法并采用拉格朗日方程建立了系统的动力学方程,分别设计了基于干扰观测期的LQR控制器、基于自抗扰控制原理的ADRC控制器和LADRC控制器,通过Matlab仿真验证了三种控制器的有效性。Pupek L[5]对两轮车机器人的欠驱动非线性的特点以及位置跟踪等问题提出了一种欠驱动的滑模控制方案。王涵、李艳[6]提出一种切换PID控制方法,根据车体的倾斜角和倾斜角速度进行控制器切换,实现了无人自行车的平衡控制。侯帅[7]提出了一种切换策略,使无人自行车在进行轨迹跟踪的同时仍能避开期望轨迹上的障碍物。王志龙[8]基于陀螺效应倒立摆及其自行车平衡系统,使无人自行车在静、动状态下稳定站立。Yongli Zhang等人[9]运用凯恩法建立了无人自行车动态多刚体机械系统的精确数学模型,分析了自行车轴距、质心、前叉角度、前叉轨迹和速度等结构参数的变化对自行车稳定性的影响。Alizadeh M等人[10]基于滑模控制(SMC)、故障检测(FD)和基于残差信号的故障估计(FE)的集成,提出了一种新的无人自行车机器人主动容错控制(FTC),并验证了FTSMC的创新特性。Kaiming Zhang等人[11]建立了无人驾驶自行车的非光滑动力学模型,给出了系统动力学方程的数值求解算法。FuGang Li等人[12]基于拉格朗日法对无人自行车系统进行建模,提出了串级PID控制方法,提高了系统响应速度和控制精度。Zipeng Xu等人[13]设计了变域模糊指数速度趋近律滑模控制器(VFSMC),并通过数值仿真验证了该控制器的有效性。Jiaming Xiong等人[14]提出了自行车全动力学的简化模型。Yiyong Sun等人[15]研究了多目标最优平衡控制问题,提出了不同前进速度下的模糊状态空间模型和一种改进的两阶段粒子群优化算法。Long Chen等人[16]提出了一种基于极限学习机(ELM)的鲁棒积分终端滑模(ITSM)控制方案,并验证了该控制方法具有良好的平衡性能。目前国内外关于无人自行车的研究主要集中于平衡的研究,通过使用不同控制策略设计控制器以及使用不同方法建立不同的动力学模型,研究系统的鲁棒性。而负载作为自行车基本功能之一,对无人自行车整体的动态特性、驱动能力和平衡能力等方面有着重要的影响,但是这方面的研究却鲜有文献涉及。

本文以一台无机械平衡调节装置的无人自行车为对象,将无人自行车查普雷金动力学模型线性化处理;引入两种控制器,通过数值仿真和物理样机实验,分析得到四种质量下、四种竖直位置下负载对无人自行车的动态特性、驱动能力和平衡能力等方面的影响规律。

1 无人自行车模型

1.1 物理样机

无人自行车物理样机如图1所示,主要由车架、车把、前轮和后轮共四个部分组成。

▲图1 无人自行车物理样机实物图

无人自行车物理样机机构简图如图2所示。

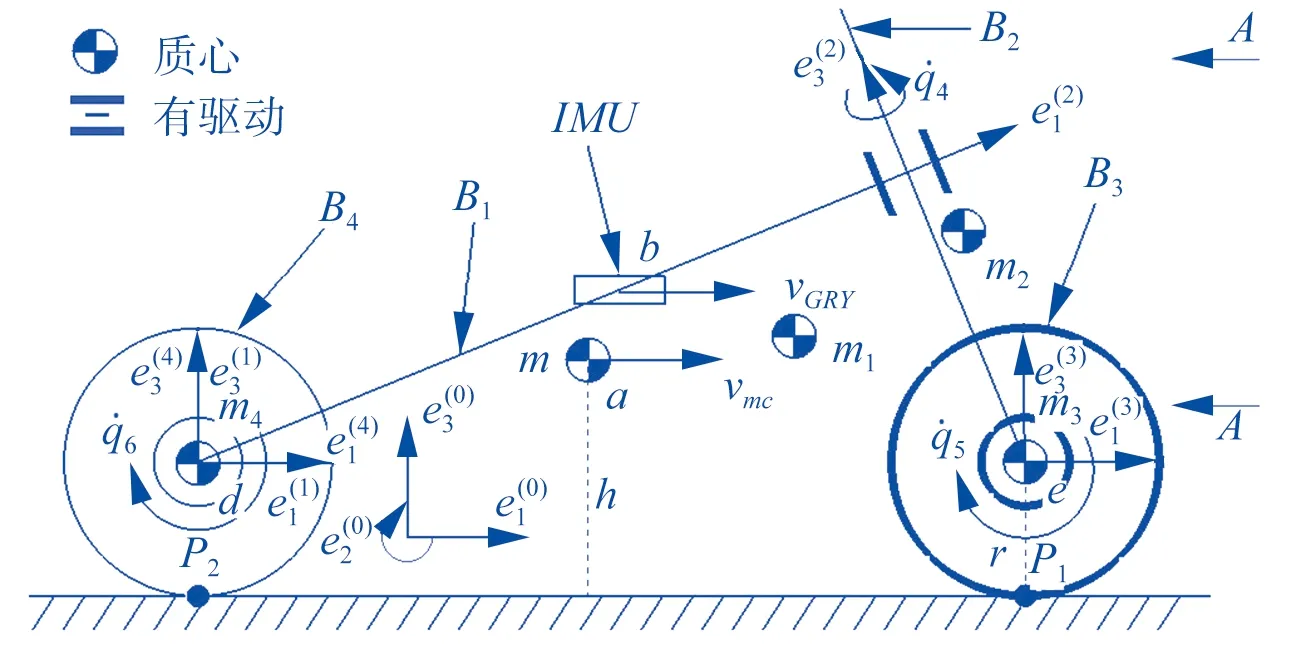
▲图2 无人自行车物理样机机构简图

通过测量solidworks中无人自行车物理样机的三维模型,得到物理样机的物理参数,如表1所示。

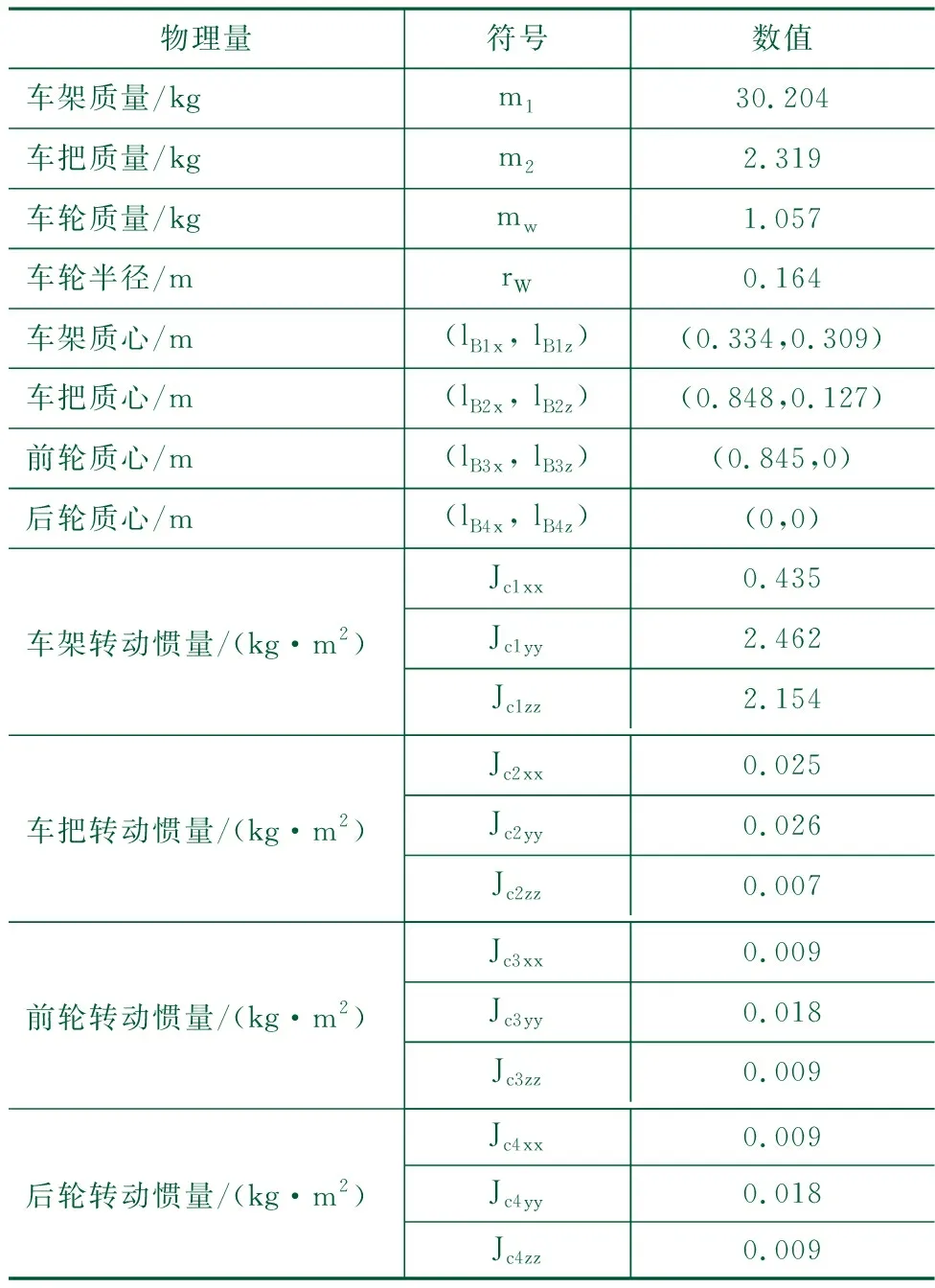
表1 无人自行车物理参数

1.2 动力学模型

无人自行车查普雷金动力学模型[17]如下所示:

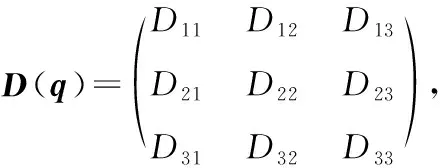
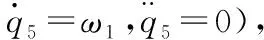
(1)

上(1)式可以继续转换为如下形式:

(2)

由(2)可以得到独立广义变量的二阶导数所对应的表达式。

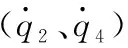
(3)

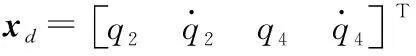
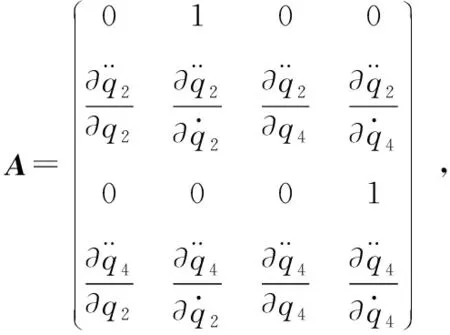
采用式(4)所示向后差商的方法对矩阵中的导数计算进行离散化。

(4)

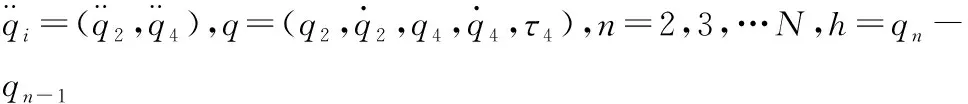
2 控制器

2.1 控制器选择

由于滑模控制器能够克服系统的不确定性,系统状态一旦进入滑模运动,能快速地收敛到控制目标。而对于全阶滑模控制器,从任何初始状态开始,在滑动模态过程中期望的运动与扰动无关。

线性二次型调节器(linear quadratic regulator,LQR)控制器可得到状态线性反馈的最优控制规律,易于构成闭环最优控制,方法简单便于实现。

所以我们选择全阶滑模控制器和LQR控制器对无人自行车进行实验研究。

2.2 控制器简介

考虑外部干扰的影响,由状态方程式(3)得

(5)

对于全阶滑模控制器而言,其控制量:

(6)

式中:eT=(0,0,0,1)(B,AB,A2B,A3B),P(A)=(A-λ1I)(A-λ2I)(A-λ3I)(A-λ4I),其中λ1～λ4是系统的期望特征值,I为4×4的单位阵。

通过附加的一阶系统补充(5)式

(7)

其中:z的初始状态由系统初始状态计算获得:

z(0)=-BTx(0)

(8)

控制器输出量Tδ(t)为x和z的不连续函数:

(9)

为了削弱控制器进行滑动模态运动时的抖振现象,用Sigmoid(s)=(1-e-js)/(1+e-js),j=1来代替符号函数sign(s)[18]。

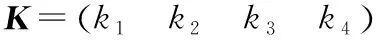
(10)

式中:Q(t)为运动约束加权矩阵,R(t)为约束控制加权矩阵,且Q(t)为半正定对称矩阵,R(t)为正定对称矩阵。[19]

3 负载调整方案

3.1 负载不同质量调整方案

由于在车架上加上负载会影响无人自行车车架的物理参数,基于数值仿真模型尽量契合物理样机实验模型的原则,先对物理样机实验的负载调整方案进行设计。

对于负载不同质量的物理样机实验,根据实际物理样机的结构特点,将负载固定在车架中部电池盒盖的上表面,负载质量m按2 kg的梯度增加,即0 kg、2 kg、4 kg、6 kg,由于器材的限制,2 kg负载方案用一块2 kg质量块实现,4 kg负载方案用两块2 kg的质量块上下叠加实现,6 kg负载方案用两块3 kg的质量块上下叠加实现。根据实验具体情况,设置无人自行车前进速度恒定为100 r/min。

对于负载不同质量的数值仿真,根据物理样机实验方案,在soldworks中的物理样机三维模型上添加同等体积和质量的负载三维模型,测量三维模型中加上负载后变化的车架物理参数,并建立变化后的车架物理参数表,如表2所示。

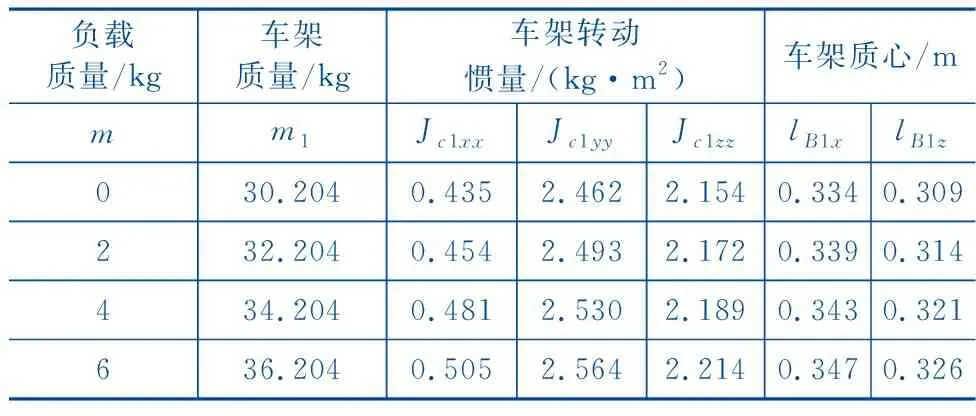
表2 负载质量变化的车架物理参数

3.2 负载不同竖直位置调整方案

和负载不同质量调整方案逻辑一样,先对物理样机实验的负载调整方案进行设计。

对于负载不同竖直位置的物理样机实验,将一块3kg的质量块固定在一块亚克力板上,然后再把亚克力板固定在车架中部电池盒盖的上表面,通过将亚克力板和电池盒盖之间垫上不同长度的套筒来实现负载竖直位置的改变,套筒长度z按30 mm的梯度增加,即套筒长度分别为30 mm、60 mm、90 mm、120 mm。根据实验具体情况,设置无人自行车前进速度恒定为100 r/min。

对于负载不同竖直位置的数值仿真,根据物理样机实验方案,在SolidWorks中的物理样机三维模型上添加同等体积和质量的3kg负载三维模型,测量三维模型中加上负载后变化的车架物理参数,并建立变化后的车架物理参数表,如表3所示。

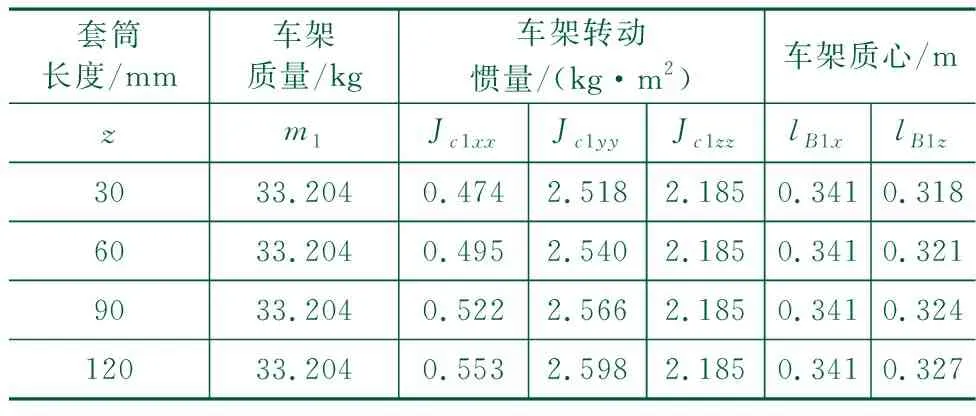
表3 负载竖直位置变化的车架物理参数

4 数值仿真

4.1 数值仿真初始化设置

使用Matlab/Simulink软件对系统进行数值仿真。

结合物理样机已有的平衡实验数据和查普雷金动力学模型,根据(4)式和表2、表3计算出模型线性化后的A、B矩阵,如表4、表5所示。

表4 负载质量变化的A、B矩阵

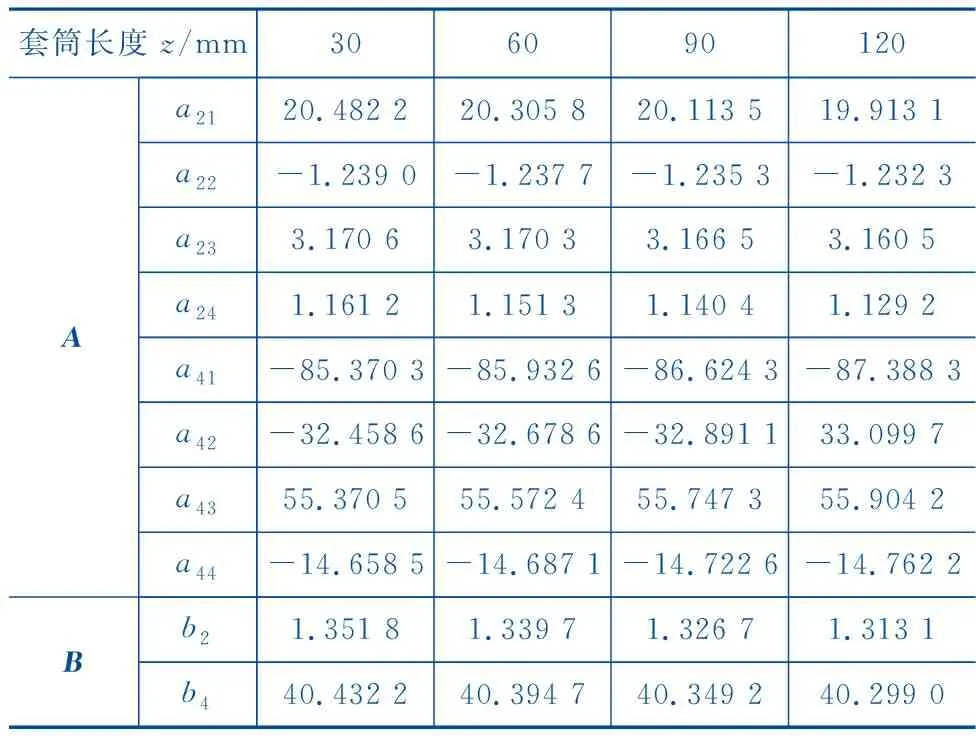
表5 负载竖直位置变化的A、B矩阵

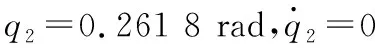
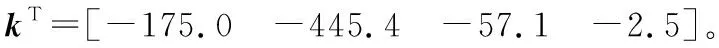
对于LQR控制器,选取加权矩阵Q=diag[100.0 0.1

1.0 0.1],R=100.0,对应反馈增益矩阵K=[16.0 2.9 1.0 0.2]。

4.2 负载不同质量数值仿真结果与分析

基于全阶滑模控制器的数值仿真结果如图3所示。

由图3仿真结果可见。

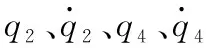
基于LQR控制器的数值仿真结果如图4所示。

由图4仿真结果可见。

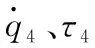
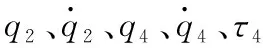
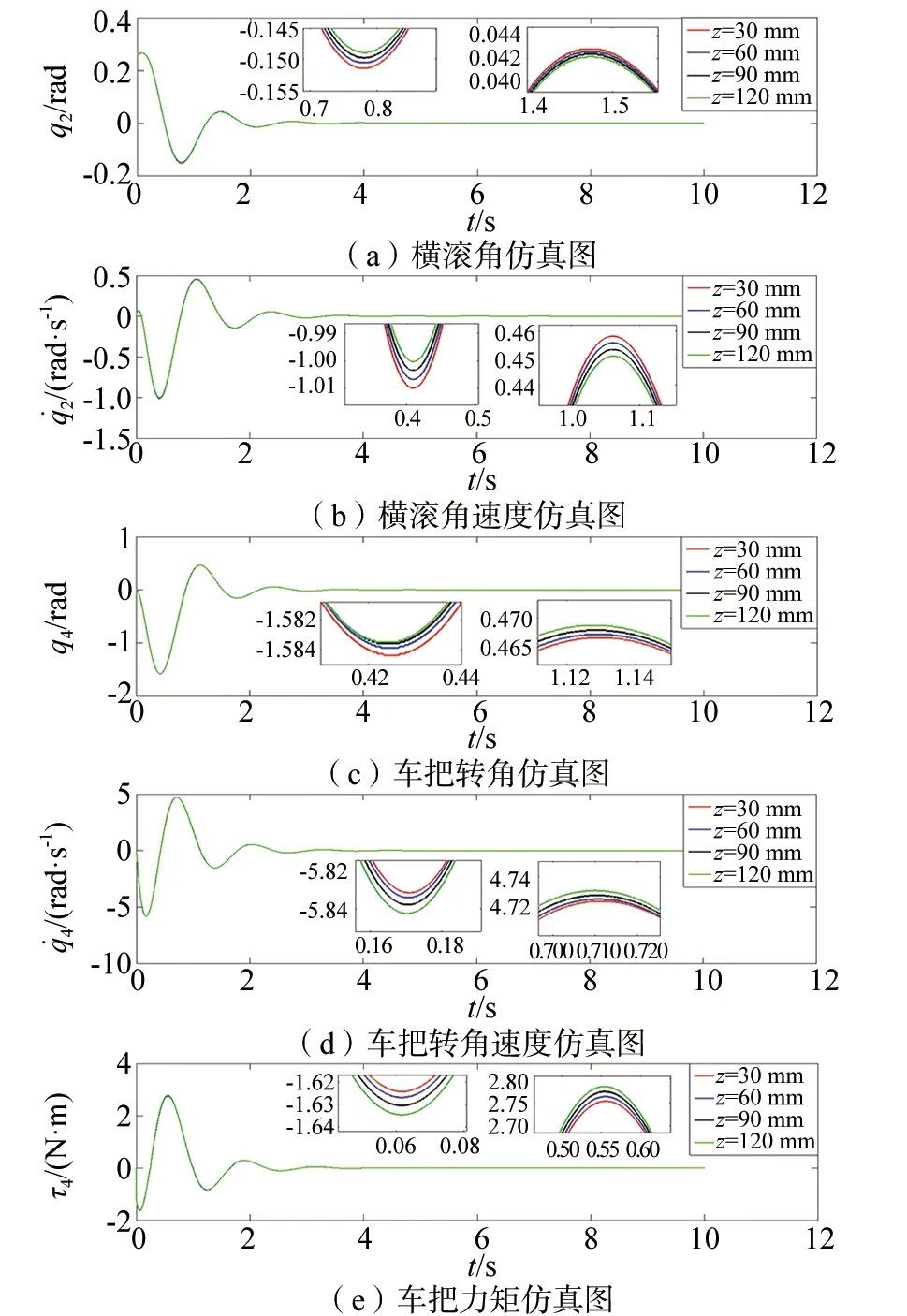
▲图3 不同负载质量下的仿真图(全阶滑模)

▲图4 不同负载质量下的仿真图(LQR)

4.3 负载不同竖直位置的数值仿真结果与分析

基于全阶滑模控制器数值仿真结果如图5所示。

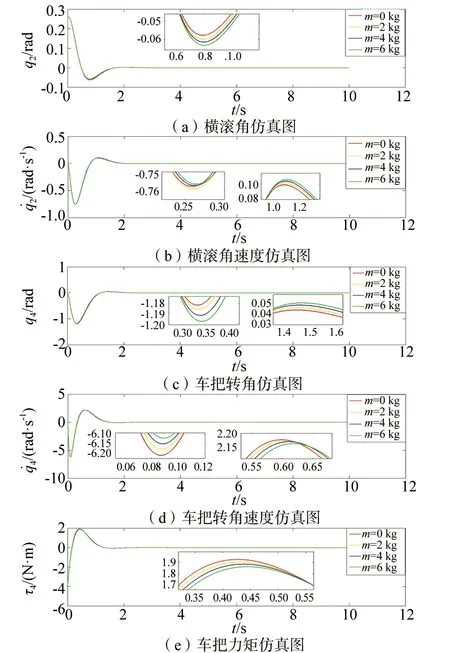
▲图5 负载不同竖直位置仿真图(全阶滑模)

由图5仿真结果可见:

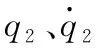
基于LQR控制器的数值仿真结果如图6所示。

由图6仿真结果可见:

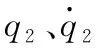
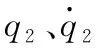
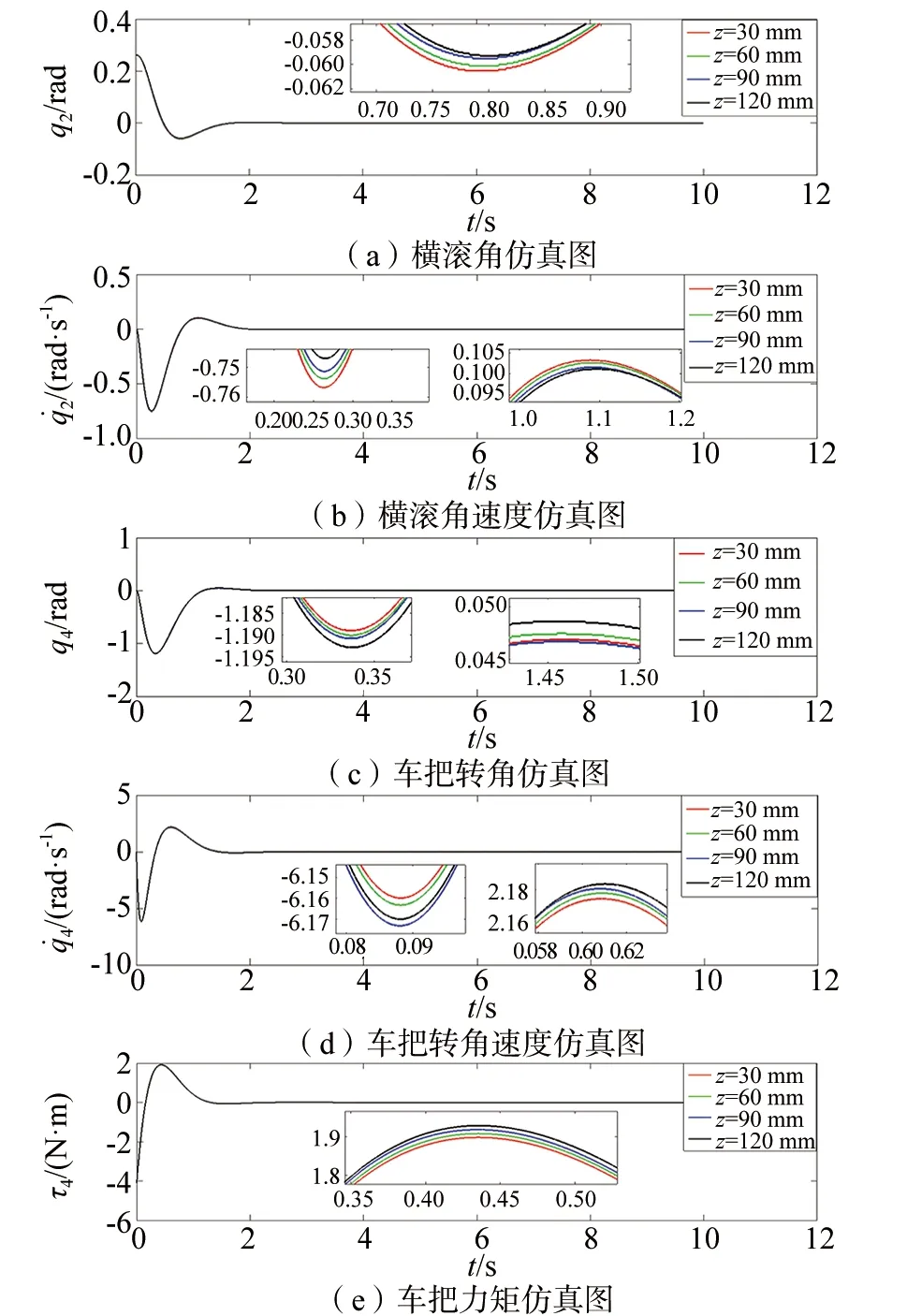
▲图6 负载不同竖直位置仿真图(LQR)

5 物理样机实验

5.1 物理样机测控系统简介

无人自行车测控系统如图7所示。

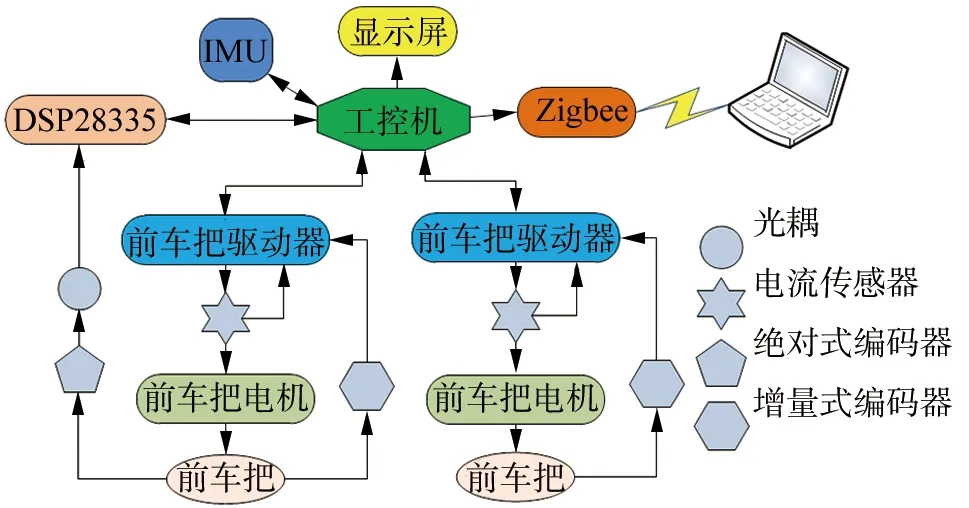
▲图7 无人自行车测控系统框图

测控系统由工控机、显示屏、数字信号处理器(DSP)、惯性测量单元(IMU)、光电编码器、光耦、电机、驱动器等组成。

其中,工控机主要用于复杂控制计算、发送控制指令、采集惯性测量单元数据;DSP主要用于采集相关传感器的信号;驱动器主要用于控制电机运动及反馈电机的状态数据;惯性测量单元采集系统姿态数据。各模块间采用RS232串行通信接口实现信息交互。

5.2 物理样机实验初始化设置

在工控机的VS2010上编写物理样机实验程序。

考虑物理样机模型与所建立的理想样机模型在结构、参数以及运行工况的差异,实验时以理想样机数值仿真的控制器参数为基础,重新选取控制器参数。

对于LQR控制器,调整反馈增益矩阵为K=[759.0 85.2 250.0 8.9]。

5.3 负载不同质量实验结果与分析

基于全阶滑模控制器的实验视频连拍图和实验数据分别如图8、9所示。

▲图8 不同负载视频连拍(全阶滑模)

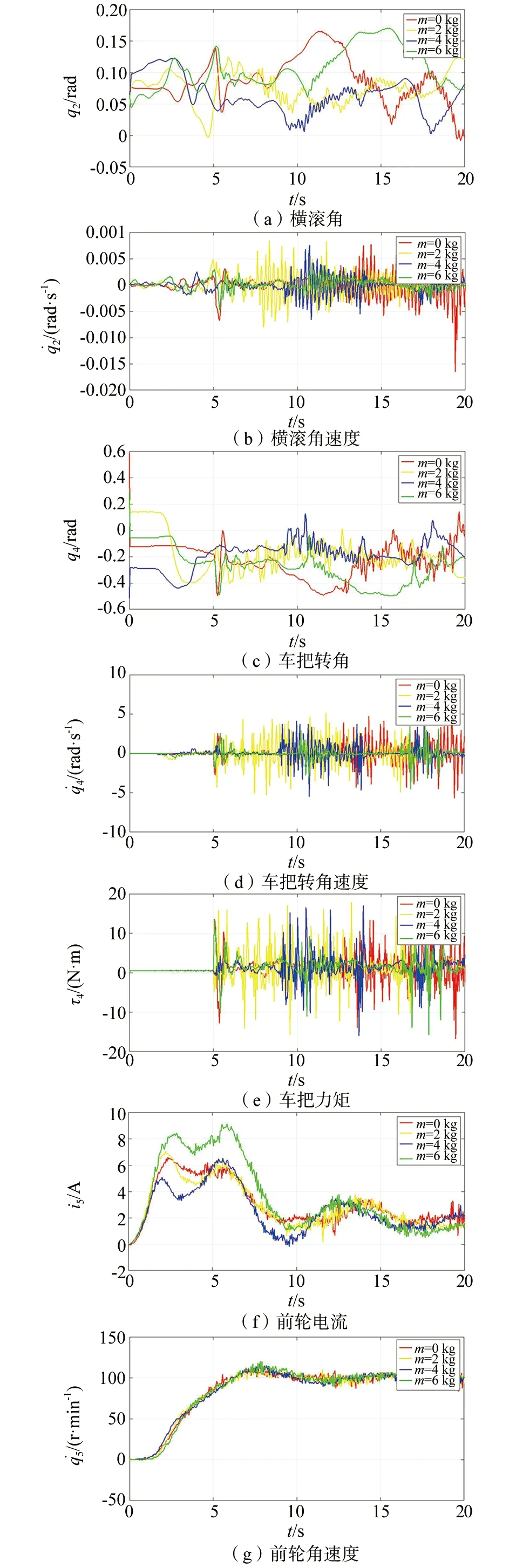
▲图9 不同负载下实验数据(全阶滑模)

以2 m一个的路障为参照物,实验视频在无人自行车脱手时开始录制。由图8可知,无人自行车均实现了负载不同质量下的侧向动态平衡。

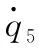
τ4的范围从m=0 kg情况下的(-9.18～13.66) N·m到m=2 kg情况下的(-12.57～13.87)N·m,再到m=4 kg情况下的(-4.64～9.17)N·m,最后到m=6 kg情况下的(-3.517～5.98)N·m,从整体来看可见,随着负载竖直位置z的增加,τ4的超调量有减小的趋势。

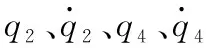
基于LQR控制器的实验视频连拍图和实验数据分别如图10、11所示。

以2 m一个的路障为参照物,实验视频在无人自行车脱手时开始录制。由图10可知,无人自行车均实现了负载不同质量下的侧向动态平衡。

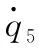
τ4的范围从m=0 kg情况下的(-9.18～13.66)N·m到m=2 kg情况下的(-12.57～13.87)N·m,再到m=4 kg情况下的(-4.64～9.17)N·m,最后到m=6 kg情况下的(-3.517～5.98)N·m,从整体来看可见,随着负载竖直位置z的增加,τ4的超调量有减小的趋势。

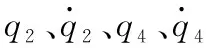
▲图10 不同负载质量实验视频连拍(LQR)

▲图11 负载不同质量下实验数据(LQR)

5.4 负载不同竖直位置实验结果与分析

基于全阶滑模控制器的实验视频连拍图和实验数据分别如图12、13所示。

以2 m一个的路障为参照物,实验视频在无人自行车脱手时开始录制。由图12可知,无人自行车均实现了负载不同质量下的侧向动态平衡。

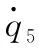
▲图12 不同竖直位置下视频连拍(全阶滑模)

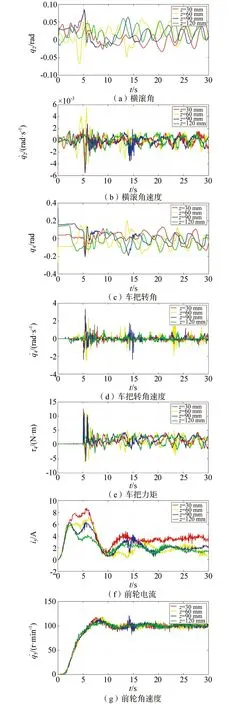
▲图13 不同竖直位置下实验数据(全阶滑模)

q2的范围从z=30 mm情况下的(-0.034～0.050)rad到z=60 mm情况下的(-0.011～0.041)rad,再到z=90 mm情况下的(-0.021～0.060)rad,最后到z=120 mm情况下的(-0.025～0.050)rad,从整体来看可见,随着负载竖直位置z的增加,q2的超调量有减小的趋势。

τ4的范围从z=30 mm情况下的(-0.444～4.309)N·m到z=60 mm情况下的(-1.758～4.504)N·m,再到z=90 mm情况下的(-1.304～3.992)N·m,最后到z=120 mm情况下的(-2.054～4.177)N·m,可见随着负载竖直位置z的增加,τ4的超调量有增大的趋势。

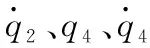
基于LQR控制器的实验视频连拍图和实验数据分别如图14、15所示。

以2 m一个的路障为参照物,实验视频在无人自行车脱手时开始录制。由图14可知,无人自行车均实现了负载不同质量下的侧向动态平衡。

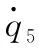
τ4的范围从z=30 mm情况下的(-12.66～15.91)N·m到z=60 mm情况下的(-17.84～14.60)N·m,再到z=90 mm情况下的(-7.22～12.97)N·m,最后到z=120 mm情况下的(-17.77～16.73)N·m,从整体来看可见,随着负载竖直位置z的增加,τ4的超调量有增大的趋势。

▲图14 不同竖直位置下视频连拍(LQR)

▲图15 不同竖直位置下实验数据(LQR)

6 结论

本文以一种无机械平衡调节装置的无人自行车,研究无人自行车侧向平衡运动时的负载特性。首先对无人自行车查普雷金模型线性化处理,然后引入全阶滑模和LQR控制器,调整控制参数以实现侧向平衡控制,最后加装负载和套筒,分别进行负载不同质量和不同竖直位置的数值仿真实验和物理样机实验。

研究结果表明,在实验限定范围内,无人自行车仍能保持动态平衡状态。不论是基于全阶滑模控制器还是LQR控制器,在理想状态下,随着负载质量的增加,车架横滚角和车把转角的超调量增大,车把力矩的超调量均减小,在已知负载质量的范围时,有利于车把电机的选型;由于系统的总质量增加,起动力矩也增大,前轮驱动电机宜使用更大输出力矩的电机;同时系统的总质量增加,系统总功耗会增大,供电电池宜选用容量较大的电池。不论是基于全阶滑模控制器还是LQR控制器,在理想状态下,随着负载竖直高度的增加,车架横滚角和横滚角速度的超调量均减小,车把转角速度和车把力矩的超调量均增大,车把电机宜使用更大输出力矩的电机。

研究结果可为无人自行车相关实验的电机型号和电池容量选用提供一定的参考。