平衡分布自适应的变工况轴承故障迁移诊断研究

王廷轩，刘韬，刘应东，王振亚

（昆明理工大学 机电工程学院，昆明 650500）

轴承作为旋转机械零部件的重要组成部分，被广泛应用于制造、航空等领域。如何智能准确地识别轴承健康状况，对判断设备可靠性、保障生产安全具有重大工程意义[1]。传统机器学习故障诊断研究基本遵循样本集满足同分布，且依赖于大量标签和人工经验提取特征。如支持向量机[2]、极限学习机[3]和决策树[4]等理论都被用于轴承故障的智能模式识别。然而实际工程现场中，由于随机干扰和生产工况等影响，轴承的监测信号及特征无法保证同分布，甚至存在样本缺失。

迁移学习由于具备获取先验知识并复用至相似新任务的能力被引入变工况条件下的轴承故障诊断，特别是实际工程中的小样本问题。雷亚国等[5]构建深度残差网络，并施加领域适配正则项约束，构建出深度迁移模型，实现了实验样本到机车工程样本的跨域迁移的故障。王肖雨等[6]利用自适应噪声完整经验模态分解（CEEMDAN）重构出峭度较大的固有模态分量（IMF），并映射到流形空间，通过流形特征动态分布减小源域和目标域样本分布差异，进而实现轴承的故障诊断。王廷轩等[7]利用二维时频图和多核最大均值差异（MK-MMD）度量样本分布差异的领域自适应轴承跨域故障迁移诊断方法，并取得良好的实验效果。康守强等[8]提出频域和时域的多域特征构建，并用子空间对齐改进核映射方法，在高维空间上促进样本特征的无监督对齐，优化了领域间的边缘分布和条件分布。沈飞等[9]提出频谱相似度初筛源域和目标域样本，并利用谱质心均值距离指标分离出分布差异较大样本。这些算法虽然能对轴承变工况问题进行迁移，但难以处理样本缺失问题且迁移过程中对样本标签依赖较高。

针对工程中样本缺失和标签获取困难等数据驱动问题，本文提出平衡分布适应（BDA）算法和K-最近邻[10]（k-Nearest neighbor,KNN）分类算法结合的变工况轴承故障诊断方法。该方法首先提取轴承信号的时域特征，并通过Fisher 准则优选特征。其次，将筛选后特征向量映射至低维的可再生希尔伯特空间，引入MMD 距离作为分布度量准则，改善领域特征的边缘分布差异和条件分布差异。最后，利用KNN 分类器对故障特征实现故障迁移诊断。与TCA、JDA 等方法相比，本文方法在同实验平台和跨实验平台变工况条件下的轴承故障迁移诊断任务中，其准确率和鲁棒性均有了明显的优势。

1 理论基础

1.1 特征变换迁移法

迁移学习[11]（Transfer learning）是通过缩小源域和目标域样本的边缘分布和条件分布的距离，实不同对象工作台间相同故障模式的辨识。特征变换迁移目标是通过学习一个特征变换T来减小正则化项R(·,·)，其目的是为了寻找一个非线性映射 φ(·)，使得特征变换后的源域边缘概率分布P[φ(xs)]和目标域边缘概率分布P[φ(xt)]的距离尽可能小，同时源域条件概率分布P[ys|φ(xs)]和目标域条件概率分布P[yt|φ(xt)]的距离也尽可能小，其联合概率分布差异可表示为

1.2 最大均值差异

最大均值差异[12]（Maximum mean discrepancy，MMD）是通过均值统计评价样本分布差异。源域和目标域样本的MMD 距离表达式为

式中：ns,nt分别为源域和目标域的样本个数；xsi,xti分别为源域和目标域样本；‖·‖H为可再生希尔伯特空间（Reproducing kernel hilbert space，RKHS）范数。

边缘概率分布MMD 距离表达式为

条件概率分布MMD 距离表达式为

1.3 平衡分布自适应

变工况下，轴承的源域和目标域样本边缘分布与条件分布所占权重不同，类别适配的平衡分布自适应方法[13]（Balanced distribution adaptation,BDA）可以来解决该迁移问题。BDA 改善了源域和目标域的联合概率分布差异，通过最大化散度，引入平衡因子u，并通过不断调整u值，从而调节适配过程中边缘分布差异与条件分布差异权重，实现不同的迁移诊断。

引入平衡因子u的BDA 源域和目标域样本间MMD 距离可以表示为

核函数核心优化目标为

构建最终BDA 方法的MMD 矩阵

1.4 Fisher 线性判别及分析

Fisher 线性判别分析[14]（Fisher discriminant analysis,FDA）可辨别特征相关性且实现特征有监督线性降维，其基本原理是将样本点映射至一条直线或者超平面上，使得映射后的同类样本间的样本方差最小，而不同类别间的样本均值之差最大。

设训练样本X=[x1,x2,···,xn]，共有K个类别；第i个样本xi映射到直线w得到yi=wTxi，i=1,2,···,n，类间散度矩阵SB，表达式为：

类内散度矩阵Sw表达式为

对于多分类问题，FDA 方法会得到投影到向量w上的类间散度矩阵SB和类内散度矩阵Sw，求解目标函数，其目标函数优化表达式为

计算特征的相关性ri，其相关性表达式为

若ri数值越大，证明同类样本方差较小，异类样本间的均值越大，则判别性越好。

1.5 BDA-KNN 的轴承故障迁移诊断

为了验证BDA 算法在变工况条件下轴承故障迁移诊断效果，本文设计了一个同实验平台和跨实验平台的验证实验，如图1所示。实验选取国外公开轴承数据和实验室试验台采集轴承数据两种数据集作为样本，实现同实验平台和跨实验平台两类变工况轴承迁移诊断任务。

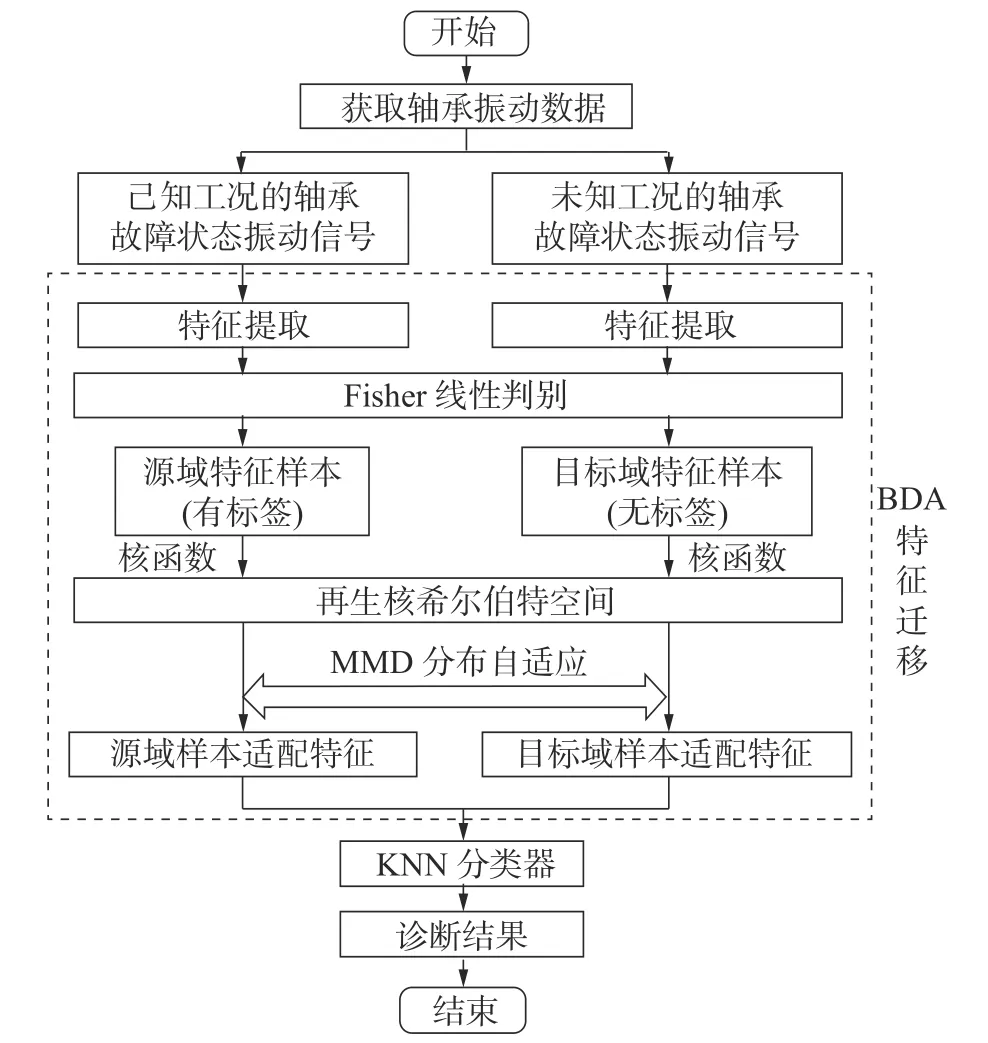
图1 平衡分布自适应故障迁移诊断流程图Fig.1 Flowchart for balancing distribution adaptive fault transfer diagnosis

实验的具体步骤如下：

步骤1数据集划分。将原始轴承振动数据依据不同的工况划分为70%训练集（源域样本）和30%测试集（目标域样本），作为迁移模型的输入样本。

步骤2特征提取。对划分后的数据集提取轴承故障的时域特征。

步骤3 Fisher 线性分析。根据特征向量进行类内类间的线性分析，选择占比权重较大的特征向量。

步骤4 BDA 方法适配。将提取的源域和目标域特征向量利用BDA 方法进行分布适配，得到适配后的源域和目标域样本。

步骤5 KNN 分类诊断。将分布适配后的特征样本，利用KNN 分类算法进行故障诊断。

2 仿真信号分析

仿真4组符合正态分布的二维随机数组，两两一组将其划分为两类样本，模拟仿真变工况条件下源域和目标域故障类别的轴承特征样本。将生成后的仿真样本分别通过迁移成分分析[15]（Transfer component analysis,TCA）、联合分布自适应[16]（Joint distribution analysis,JDA）、BDA 进行迁移学习，对比各类算法的分布适配情况，其仿真样本分布散点图和概率密度曲线如图2（a1）和图2（b1）所示。

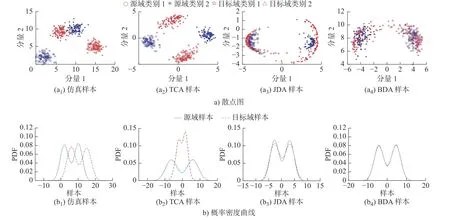
图2 仿真样本分布适配散点图及概率密度曲线Fig.2 Scatter plot and probability density curve of simulated sample distribution adaptation

由图2（a2）和图2（b2）可知，经TCA 分布适配后，仿真样本源域和目标域样本的整体分布距离明显减小，但同一类别的源域和目标域的分布距离仍较大，TCA 对减小领域样本的边缘分布具有一定作用，但改善非同类样本之间的条件分布差异微乎其微。图2（a3）和图2（b3）是JDA 分布适配后的源域和目标域仿真样本整体分布距离，可以看到JDA 也可以优化相同类别样本分布距离，但对非同类样本间的拉近效果仍较差。图2（a4）和图2（b4）是通过BDA 适配后的结果，源域和目标域样本的概率密度曲线基本重合，且两领域中相同类别的样本也能较好的吻合，证明BDA 算法对边缘分布和条件分布距离均明显减小，适配后样本分布优于TCA 和JDA。通过BDA 适配后的概率密度曲线对比可知，BDA适配的样本能够最大保持原始样本分布规律。据仿真结果证明，上述所涉及的样本分布自适应算法能够较好解决两类分布不同样本的迁移适配问题，且BDA 算法优于其他两类算法。

3 实验验证与分析

3.1 实验设计

本文设计两个案例完成同实验平台和跨实验平台采集的变工况条件下轴承故障振动信号进行故障迁移诊断，并对本文方法展开相关实验验证，证明本方法具备有效性和鲁棒性。本文选取两类试验台来分别验证同实验平台迁移和跨实验平台迁移。其实验设计如下：

实验A：如图3a）所示，实验数据采用美国凯斯西储大学[17]（Case western reserve university，CWRU）的公开轴承数据集。电机驱动端轴承型号为SKF6205，参数如表1所示。

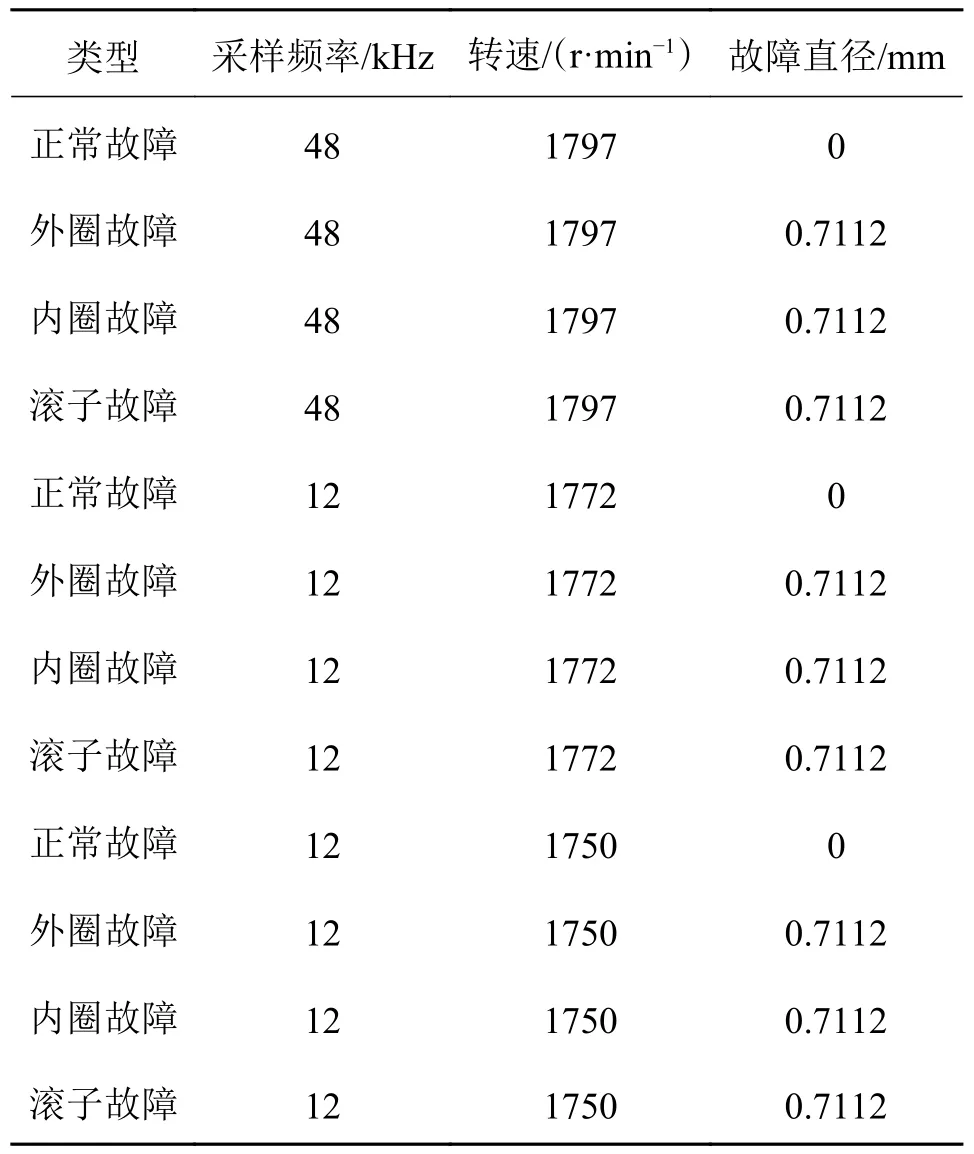
表1 CWRU 轴承样本集Tab.1 CWRU bearing sample set

图3 轴承故障试验台Fig.3 Bearing fault test rig

实验B：如图3b）所示，实验数据采用ABLT-1A型轴承寿命强化试验台所采集的轴承数据集。数据集B 的滚动轴承型号为SKF 6205，参数如表2所示。

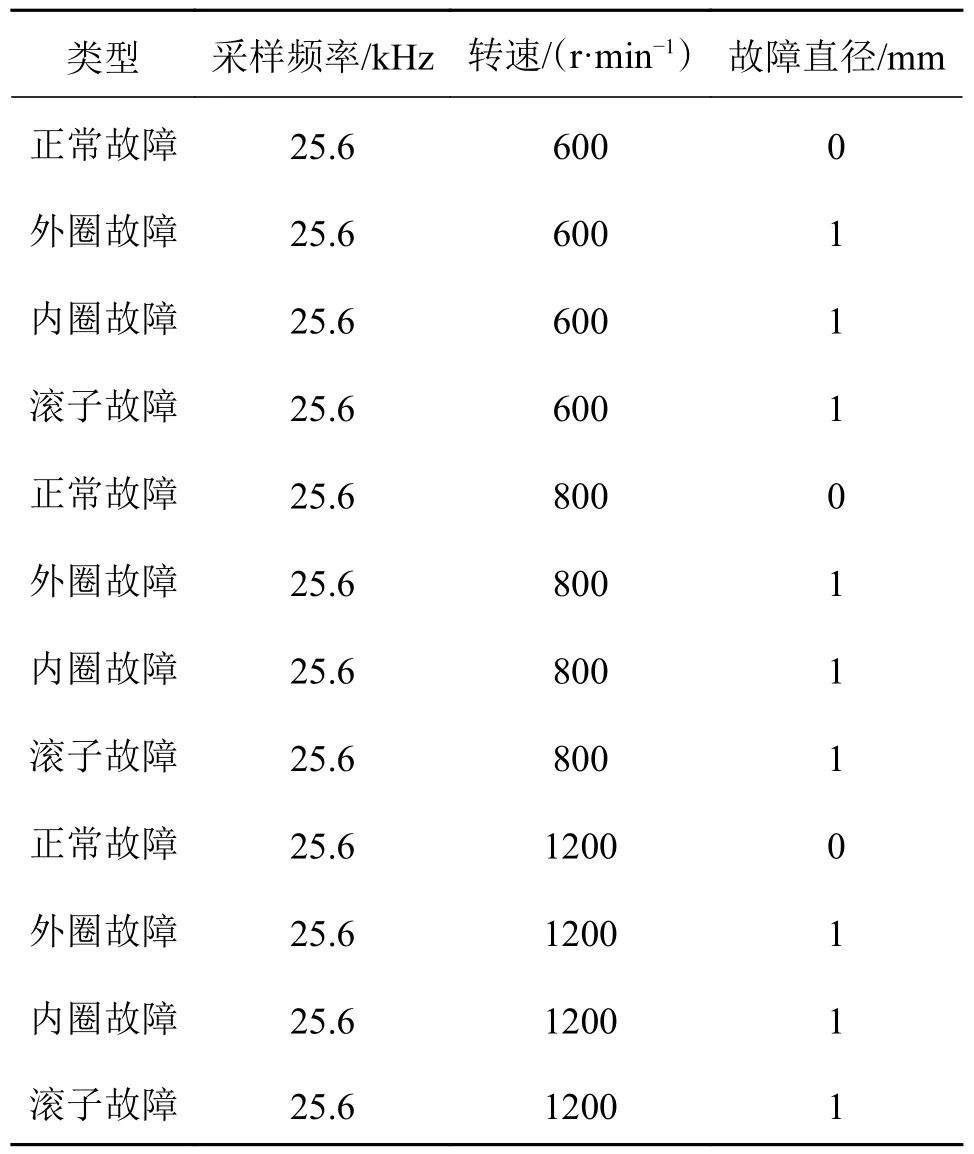
表2 实验室轴承样本集Tab.2 Laboratory bearing sample set

3.2 故障特征提取

训练样本集和测试样本集均为变工况样本，选取不同工况的故障轴承信号作为源域（训练集）和目标域（测试集）。

通过对划分后两域振动信号进行时域特征提取[16]（有效值、歪度、峭度、峰值、峰峰值、波形因数、脉冲因数、峰值因数和裕度），其时域特征函数表达式如表3所示，将提取后的特征作为迁移任务的输入样本。通过FDA 计算以上9种故障特征向量在迁移诊断中所占的权重。

表3 时域特征函数表达式Tab.3 Time-domain characteristic functional expressions

如图4计算结果显示，有效值、峰峰值、峰值、峭度、裕度和波形因数，占时域特征的前6位。选取这6类时域特征作为特征样本，作为后续迁移任务的样本输入特征。

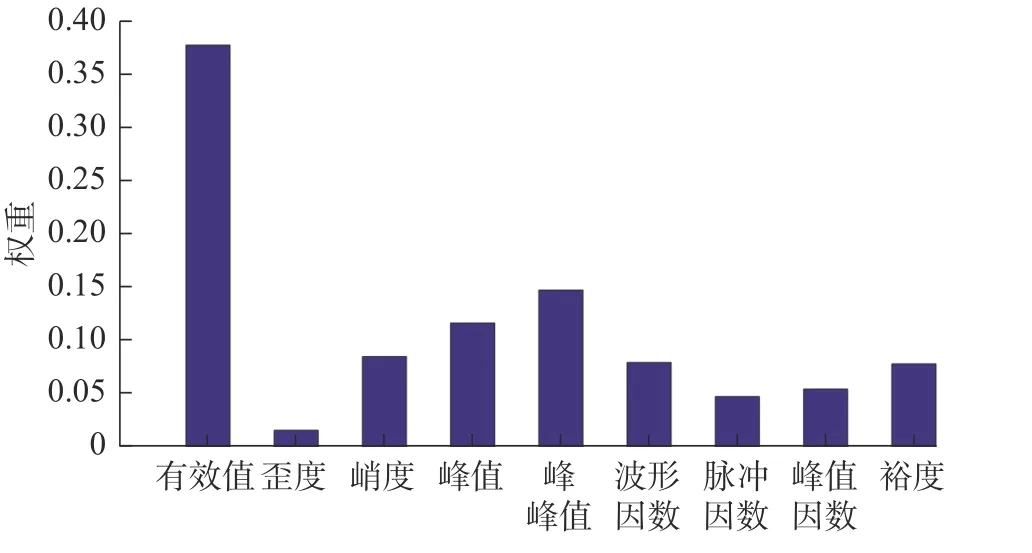
图4 时域特征所占权重Fig.4 Weights of time-domain characteristics

3.3 同实验平台的故障迁移诊断验证与分析

为了验证BDA 方法在变工况条件下轴承故障的迁移诊断效果，针对同实验平台下不同转速的迁移诊断效果进行验证与分析。

在轴承的同域变工况迁移任务中，以800 r/min→1 200 r/min 任务为例，将轴承源域和目标域样本降维并绘制散点图。对比各方法的分布散点图：图5a）所示的PCA 方法中，正常状态的源域和目标域样本分布距离较小且重合度较好，但其他3类故障源域和目标域样本之间边缘分布差异较小，样本的重合度较差，滚子故障和正常状态存在混叠，分类诊断准确率为67.13%。图5b）所示的TCA 方法中，内圈故障的源域和目标域样本边缘分布差异相较于PCA 方法明显减小，正常状态的样本分布距离重合性改善不明显，分类诊断准确率为73.29%。图5c）所示的JDA 方法中，轴承故障的源域和目标域样本区分性较高，各故障的源域和目标域样本分布距离均明显减小，外圈和滚子故障重合性较好，各故障间无明显混叠，分类诊断准确率为94.46%。图5d）所示的BDA 方法中，轴承故障的源域样本和目标域样本区分明显，各故障状态类内距离较小，类间距离较大，样本重合度较高，分类诊断准确率为100%。在同实验平台的故障迁移任务中，轴承各类故障的适配结果如图6所示，BDA 拉近轴承故障源域和目标域样本的MMD 距离近乎于零，均比低于其他方法，证明BDA 在拉近源域和目标域样本的能力最强，对变工况下的轴承样本迁移效果最优。

图5 同实验平台迁移的可视化散点图Fig.5 Visual scatter plot of transfer within the same experimental platform

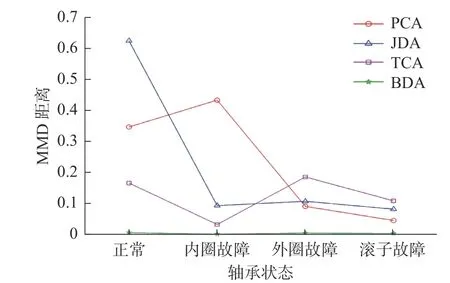
图6 同实验平台迁移的MMD 适配距离Fig.6 MMD adaptation distance of transfer within the same experimental platform

对比变工况下的各类迁移方法的诊断准确率，结果如表4所示。BDA 方法在拉近分布适配上的效果优于其他方法，准确率达到99%以上；KNN 分类和PCA 降维分类后的准确率相近，范围55%～60%之间。TCA 方法的准确率在73%～78%之间，J DA 方法的准确率在85%～89%之间。

表4 同实验平台迁移的不同分布差异准确率Tab.4 Accuracy of different distribution differences in transfer within the same experimental platform %

3.4 跨实验平台的故障迁移诊断验证与分析

为了更全面地验证BDA 方法在变工况条件下的轴承故障迁移诊断的鲁棒性，本节进行不同试验台的跨域迁移，源域选取CWRU 的轴承样本，目标域选取实验室试验台的轴承样本。

在轴承跨实验平台迁移诊断任务中，以CWRU 1 797 r/min→实验室试验台1 200 r/min 任务为例，将轴承源域和目标域样本降维并绘制散点图。对比各算法的可视化散点图可知：图7a）所示的PCA 方法，各类故障源域和目标域样本区分性较差，内圈故障被淹没，外圈故障与滚子故障存在部分混叠，正常状态类内间距较大，分类诊断准确率为44.54%。图7b）所示的TCA 方法，各类故障源域和目标域样本多数能够较好区分，滚子故障和正常状态之间出现较多混叠，外圈故障源域和目标分布差异较大，分类诊断准确率为61.73%。图7c）所示的JDA 方法中，仅少量滚子故障和外圈故障存在混叠，各故障聚类较为集中，分类诊断准确率为76.36%。图7d）所示的BDA 方法中，各故障状态的源域和目标域样本能够较好的区分，边缘分布和条件分布差异适配得以提高，类间和类内距离提升明显，领域间样本分布重合度较高，极少正常状态被误判为滚子故障。分类诊断准确率达到98.57%。

图7 跨实验平台迁移的可视化散点图Fig.7 Visual scatter plot of transfer across different experimental platforms

综上，通过跨实验平台和同实验平台迁移的结果分析，本文方法针对不同类别迁移任务具备良好的准确性和鲁棒性，改善迁移过程中的样本分布差异明显，各故障类别样本聚类效果明显。

在跨实验平台的故障迁移任务中，轴承各类故障的适配结果如图8所示,使用BDA 后，轴承各故障源域和目标域样本的MMD 距离均比其他迁移方法的更小，验证了BDA 方法在改善轴承源域和目标域样本的能力最强，变工况下的轴承样本迁移效果最优，改善适配距离具备较大的优势。

图8 跨实验平台迁移的MMD 适配距离Fig.8 MMD adaptation distance for transfer across different experimental platforms

不同转速下的各类迁移方法的诊断准确率如表5所示，BDA 在优化分布适配的效果优于其他方法，准确率达到98%以上，KNN 分类和PCA 降维分类后的准确率接近，范围58%～65%之间。TCA的准确率在78%左右，JDA 的准确率在86%～92%之间。同时验证仿真实验和同实验平台迁移的结论，BDA 方法均优于以上方法，其鲁棒性最优。

表5 跨实验平台迁移的不同分布差异准确率Tab.5 Accuracy of different distribution differences in transfer across different experimental platforms %

4 结论

通过变工况条件下同实验平台和跨实验平台的轴承故障迁移诊断可知，BDA 作为一种改善分布距离的适配迁移算法，可以改善提取特征向量之间的MMD 分布距离，降低源域样本和目标域样本的分布差异，较好地解决机器学习中样本集必须满足独立同分布的缺陷，优化了迁移效果。与其他迁移学习算法相比，诊断准确性更高，源域样本和目标域样本适配后的重合度更好，具备较好的鲁棒性和工程应用价值。为工业现场的旋转设备故障迁移诊断提供了可行的解决思路。