微凸体分布计算方法对曲面接触预测的影响

周炜，胡祺，唐进元，温昱钦

（1.湖南科技大学 难加工材料高效精密加工湖南省重点实验室，湖南湘潭 411201；2.中南大学 高性能复杂零件制造国家重点实验室，长沙 410083）

由于刀具与工件表面之间摩擦、机床高频振动和材料塑性变形等作用，机械零件表面实质为非光滑的粗糙面，这使得界面接触离散分布在表面凸出的微凸体之上，由此导致接触应力与变形、接触刚度等不同于光滑曲面假设下的结果。粗糙表面包含众多波长成分，其中波距在1 mm 以下、波长与波高之比小于50的粗糙度对接触性能影响较大，直接参与接触的微凸体即是该尺度下的形貌结构。可见，微凸体分布的有效建模对于接触性能预测而言举足轻重。

不论机械零件表面为高斯与否，考虑到摩擦性质主要取决于表面顶层，而表层结构常常取自高斯分布，因此将微凸体高度假定为高斯分布一般是有效的[1]。为便于应用赫兹接触理论，微凸体顶端通常假定为具有解析解的规则几何形状，如球形、椭球形、圆柱体、圆锥体和正弦波纹体等。相较于微凸体高度分布和形状，微凸体密度和曲率半径对接触求解影响更为显著[2]，这也是Greenwood-Williamson（GW）模型[3]关于高斯分布和球形顶端的假定有效的原因。然而，微凸体分布参数强烈依赖于采样间距，存在尺度依赖性[4]。采样间距越小，更多细小的形貌结构被呈现出来，所得微凸体曲率和数量随之增大。为减小采样间距的这种不利影响，基于滤波[5]或拟合[2]思想去除过小尺度下的形貌结构，使得微凸体分布参数的计算更加稳定。此外，从分形理论另辟蹊径，建立微凸体接触的多尺度模型[6]，也为解决微凸体分布参数的计算稳定性问题提供了选择。为消除GW 模型中关于微凸体高度分布、微凸体形状、各向同性、弹性变形、忽略微凸体相互作用和赫兹接触的有关假定，可分别参看相关文献[7-12]。

为确定微凸体分布参数，对粗糙表面采样获得高度序列后，一方面可基于微凸体识别策略，由参数定义直接计算得到[13]，另一方面，可先计算零至4阶谱矩，由随机过程理论方法估算得到[14-15]。参数定义法对微凸体识别过程中所用点数较为敏感，Pogačnik 和 Kalin 等对此进行了讨论[16]，发现三点定义法最为稳定、可靠。相比于参数定义法，Kalin[17]和周炜等[18]研究发现谱矩法计算微凸体分布参数存在偏差。Pawar 等[19]就谱矩法偏差对接触求解的影响进行了探讨，发现微凸体密度是导致两种计算方法接触求解差别的主要原因，不过，该工作限于粗糙平面接触，没有计入微凸体平均高度的作用，也没有考虑载荷水平、高通滤波等因素的影响。

当前，参数定义法和谱矩法都被广泛用于计算微凸体分布参数。厘清基于这两种方法开展GW 接触分析所产生的差异，对于粗糙表面接触预测具有重要参考意义。本文针对粗糙曲面接触，利用快速傅里叶变换（FFT）仿真得到不同统计分布下的粗糙表面随机样本，分别基于三点定义法和谱矩法对仿真样本开展GW 接触分析，对两种计算方法所得接触预测结果进行对比讨论，期望为微凸体峰点分布参数计算提供有益思考。

1 方法与原理

1.1 微凸体分布参数计算

为便于理论分析，工程表面常常被近似为具有高斯高度分布和幂指数衰减型自相关分布的理想表面，其高度序列[z]描述为[1]：

式中：ϕ为[z]概率密度分布；μ和σ分别为[z]均值与标准偏差；R为自相关性；τ为滞后距离；ϑ为高通滤波常数，代表使用不同截止长度进行高通滤波，用以消除长波成分引起的不稳定性，常取-0.844、-1和-2.3；β为相关长度，β=0对应于高斯白噪声。

对于粗糙度轮廓 [z]，根据三点定义法，zi成为微凸体峰点的条件为[13]

所有满足式（2）的zi构成微凸体峰点高度分布[ξ]，其平均高度ξavg和标准偏差σξ定义为：

式中np为微凸体峰点数。

微凸体峰点曲率κ定义为

式中 ∆为采样间距。曲率半径rp为曲率倒数，平均曲率半径定义为[14]

微凸体峰点密度定义为[1]

式中：L为采样长度；n为采样点数。

采用三点定义法识别微凸体峰点，依据式（3）～式（7）计算确定微凸体分布参数。

Nayak[14]利用随机过程理论建立了微凸体峰点分布模型，其高度和曲率分布为：

假设微凸体峰点[ξ]满足高斯分布，McCool 推导了微凸体平均高度ξavg和标准偏差σξ为[15]：

将微凸体平均高度式（11）代入式（9），近似得到微凸体平均曲率半径为

微凸体峰点密度为[14]

根据式（11）～式（14），由谱矩m0、m2和m4计算微凸体分布参数。

1.2 粗糙曲面接触计算

GW 模型将粗糙表面接触视为具有相同曲率半径rp、高度[ξ]呈高斯分布的微凸体之间的接触，如图1b）所示。其中，ω为微凸体压缩量，d为相对于微凸体平均高度的间距，h为相对于表面平均高度的间距，ys为微凸体平均高度与表面平均高度的差值。不难知道，ys=ξavg。

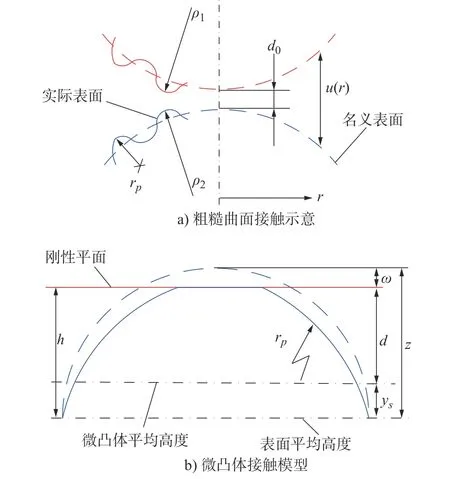
图1 接触模型示意图Fig.1 Schematic diagram of the contact model

对于刚性平面与弹性粗糙曲面接触，接触面积A、接触合力P、接触半宽C和接触微凸体数N与间距u存在如下关系[20]：

由式（11）和式（12）可知，当频带宽度系数α增至一定程度，微凸体高度分布[ξ]与粗糙表面高度分布[z]标准偏差近似相等，即σξ=σ，由此得到。由于前述两种微凸体分布参数计算方法所得微凸体分布标准偏差σξ、微凸体平均曲率半径和微凸体密度η存在偏差，必然导致其接触求解存在差异。从图1b）不难发现，刚性平面到粗糙表面间距h、刚性平面到微凸体间距d和微凸体与粗糙表面平均高度之差ys满足

注意到ys=ξavg，这表明对于给定间距h，微凸体平均高度ξavg计算偏差将作用于间距d。故此，预测接触性能随间距h变化时，需要考虑微凸体平均高度ξavg的影响。

2 结果与讨论

为研究微凸体分布参数计算方法对接触性能预测的影响，利用FFT 法重构获得不同统计分布下的粗糙表面随机样本，分别采用2.1节所述三点定义法和谱矩法计算仿真样本微凸体峰点分布参数，由2.2节粗糙曲面接触分析方法对仿真样本进行接触计算。接触计算有关参数取值如下：弹性模量E=0.206 N/μm2，泊松比ν=0.3。

2.1 接触求解对比分析

不同载荷下，相关长度β=50，高通滤波常数ϑ=-2.3，曲率半径ρ=105μm，标准偏差σ=0.05、0.10、0.50 μm 下基于三点定义法与谱矩法所得接触结果对比见图2。相比于三点定义法，在相同载荷下，基于谱矩法预测接触面积偏小、接触微凸体数偏多，这意味着相同载荷下谱矩法所得平均接触压力大于三点定义法。基于两种方法所得接触预测偏差随载荷增大而增大，随标准偏差增大而减小。不过，两种方法在相同载荷下预测的接触半宽差别很小，所预测的接触范围近乎一致。

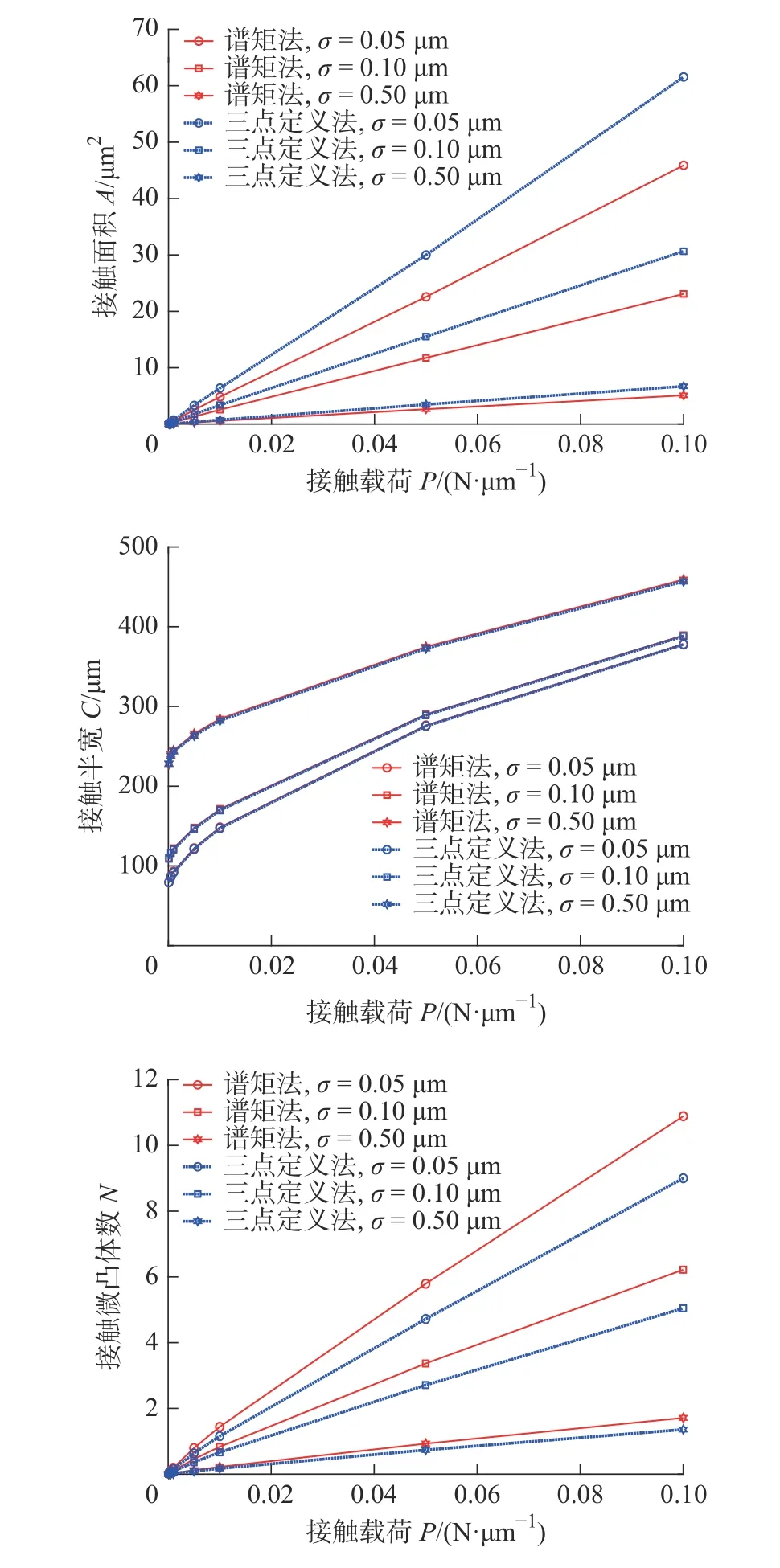
图2 不同载荷下接触求解对比Fig.2 Comparison of contact solutions under different loads

为考查其它因素对两种方法接触预测偏差的影响，开展不同相关长度、高通滤波常数和曲率半径下接触分析，得到谱矩法相对三点定义法接触预测偏差如图3所示，其中P=0.05 N/μm。可见，接触面积、接触半宽和接触微凸体数预测相对偏差变化规律并不一致。除相关长度β=0，两种方法预测偏差波动较小，接触面积与接触微凸体数预测偏差大多在20%～30%之内。相较而言，曲率半径对两种方法接触预测的偏差影响更大。

图3 两种方法接触求解相对偏差Fig.3 Relative deviation in contact solutions using two different methods

不同间距d/σ下，相关长度β=50，高通滤波常数ϑ=-2.3，曲率半径ρ=105μm，标准偏差σ=0.05、0.1、0.5 μm 下基于三点定义法与谱矩法接触求解对比见图4。相同间距d/σ下，基于谱矩法预测的接触结果均小于基于三点定义法所得结果。由于接触面积相对接触载荷预测偏差更小，使得谱矩法所得平均接触压力要更大，如图5所示。间隙d/σ越小，两种方法接触预测偏差越大。相同间距d/σ下，平均接触压力预测偏差随标准偏差增大而增大，随相关长度增大而减小。高通滤波常数和曲率半径对平均接触压力预测偏差的影响没有表现出明显的单调性。高通滤波常数ϑ=-2.3时，平均接触压力预测偏差最小。随着曲率半径增大，接触压力预测偏差最大值对应间距d也变大。这表明重载条件下，增大曲率半径有助于减小给定间距d/σ下的接触压力预测偏差。

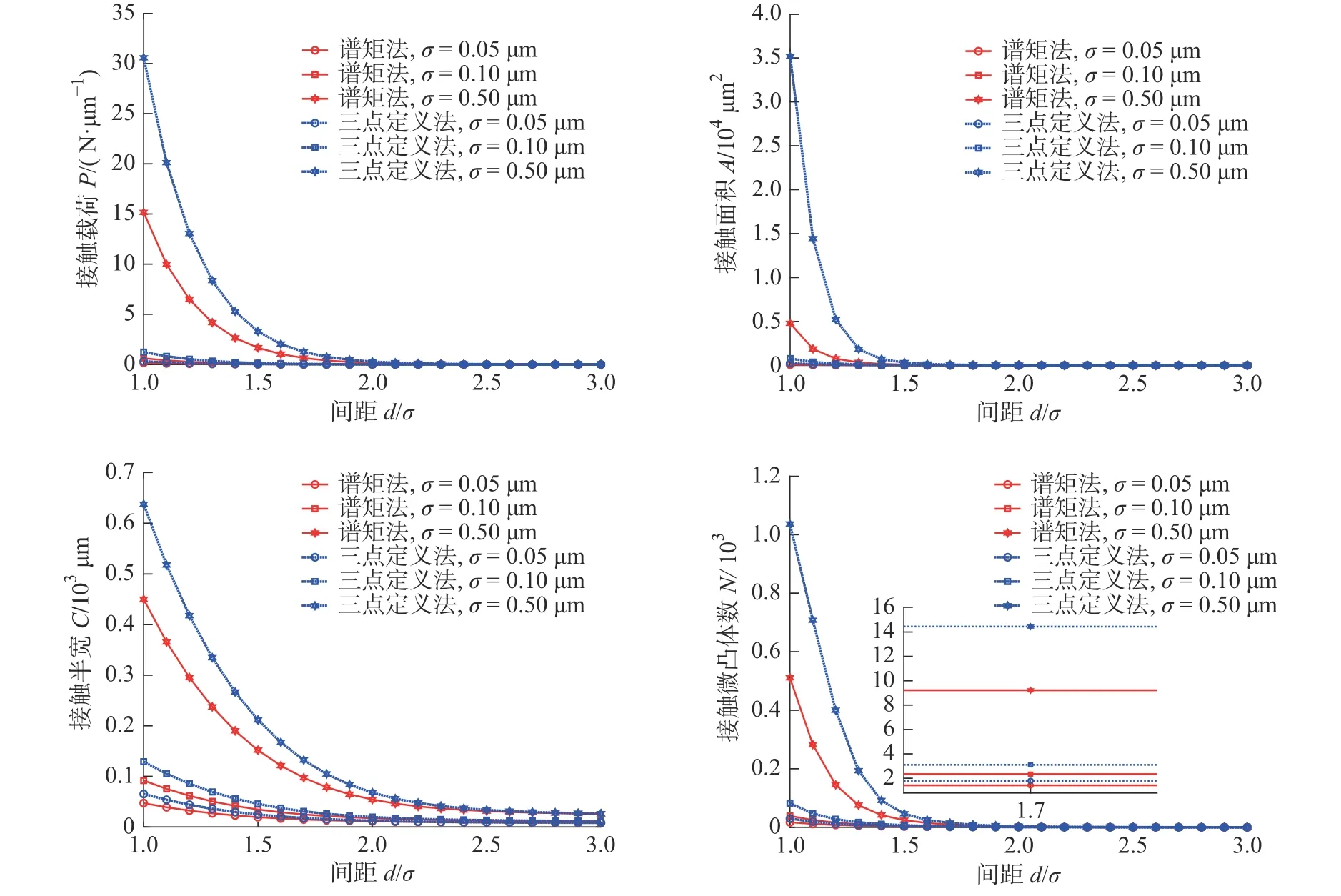
图4 不同间距d/σ 下接触求解对比Fig.4 Comparison of contact solutions at different spacings d/σ

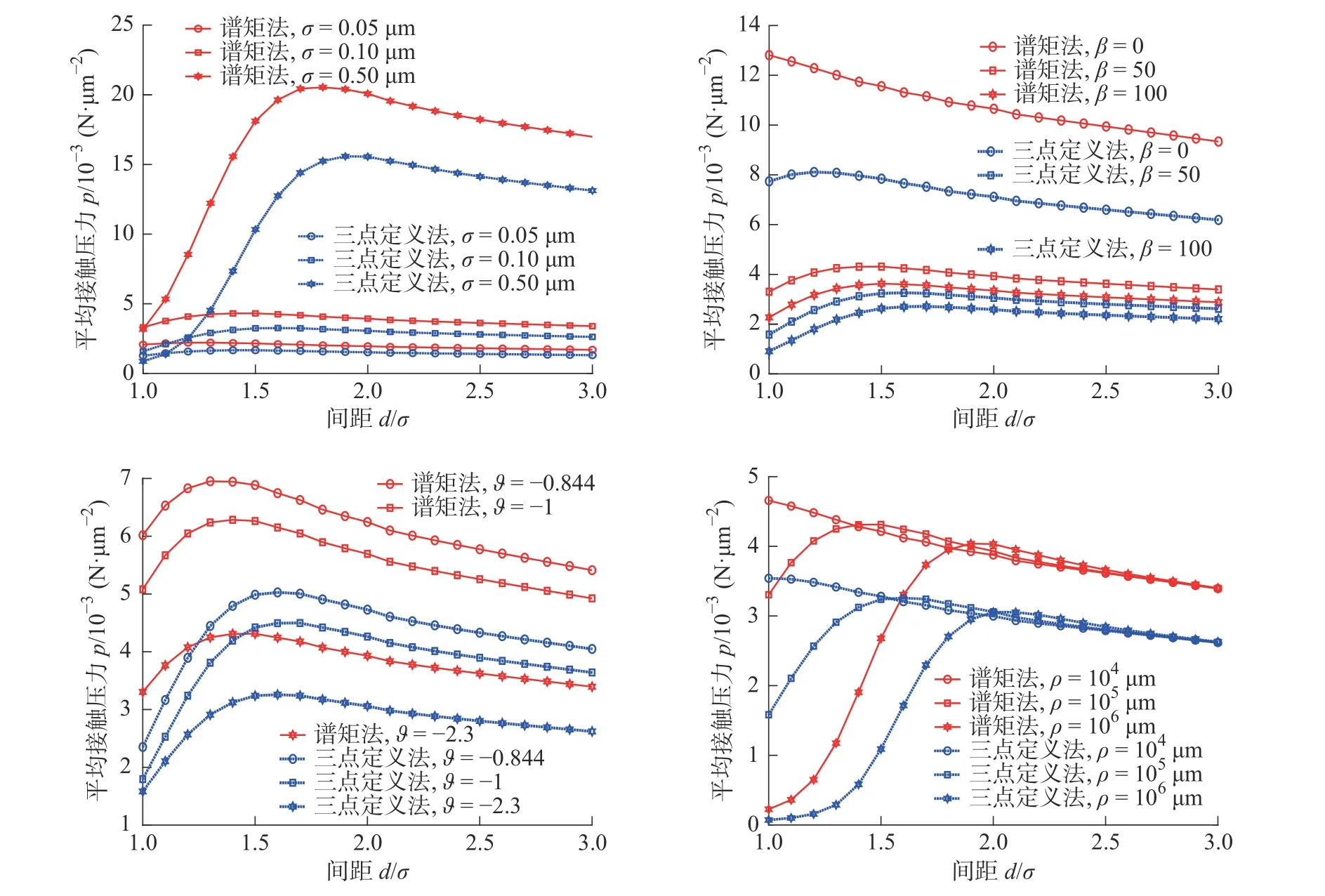
图5 不同间距d/σ 下平均接触压力求解对比Fig.5 Comparison of average contact pressure solutions at different spacings d/σ

由于间距d/σ无法体现三点定义法和谱矩法所得微凸体平均峰高计算差别的影响。为此，计算不同间距h/σ下，相关长度β=50，高通滤波常数ϑ=-2.3，曲率半径ρ=105μm，标准偏差σ=0.05、0.1、0.5 μm下基于三点定义法与谱矩法接触求解对比见图6。与间距d/σ下结果不同，考虑微凸体平均高度的计算差别之后，除较小间距h/σ下的接触面积之外，相同间距h/σ下基于谱矩法预测的接触结果均大于基于三点定义法所得结果，包括图7所示平均接触压力，且间隙h/σ越小，平均接触压力预测偏差呈减小的趋势更加明显。除此之外，平均接触压力预测偏差随其它因素变化规律与间距d/σ下所得结论相似。

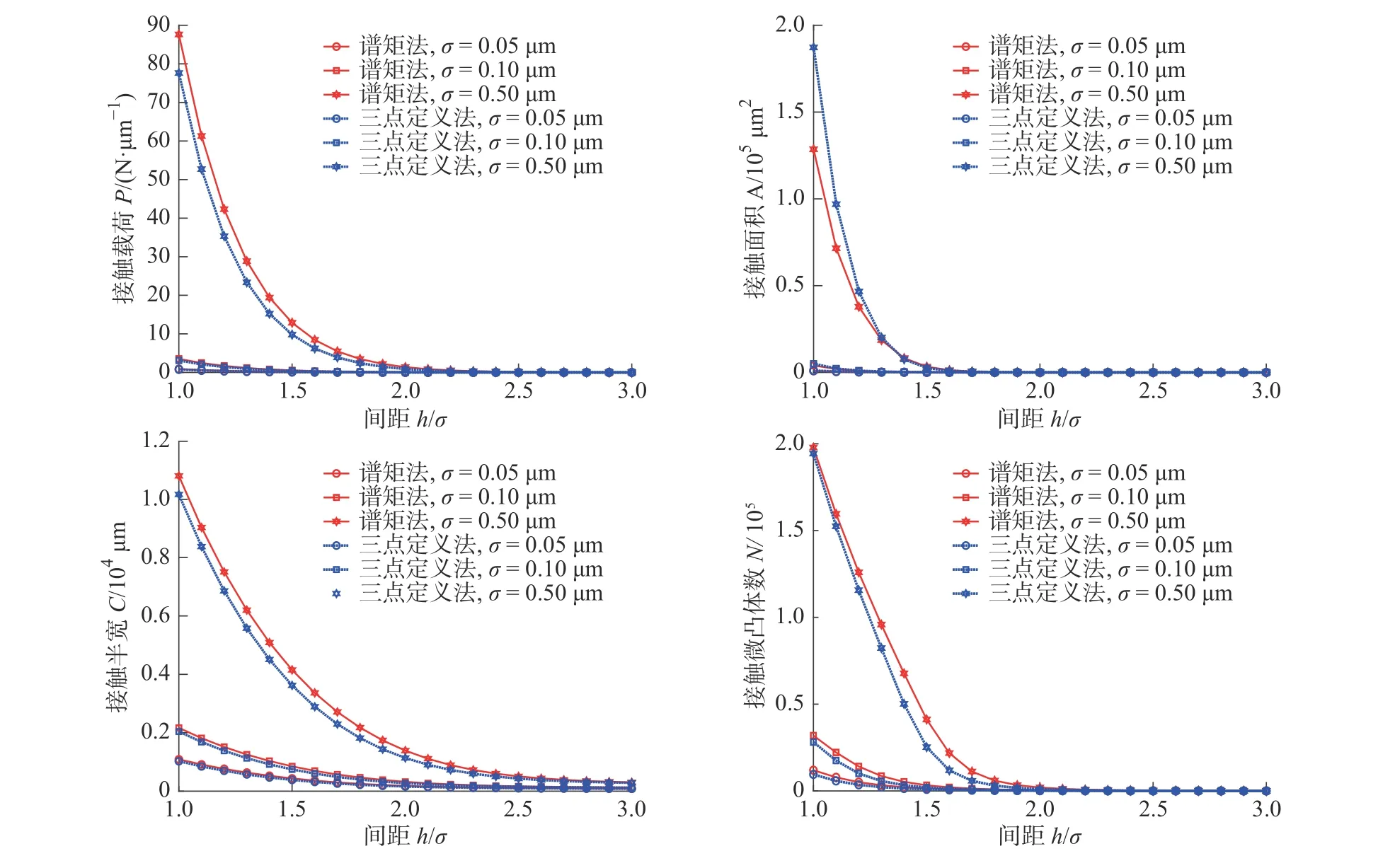
图6 不同间距h/σ 下接触求解对比Fig.6 Comparison of contact solution at different gaps h/σ

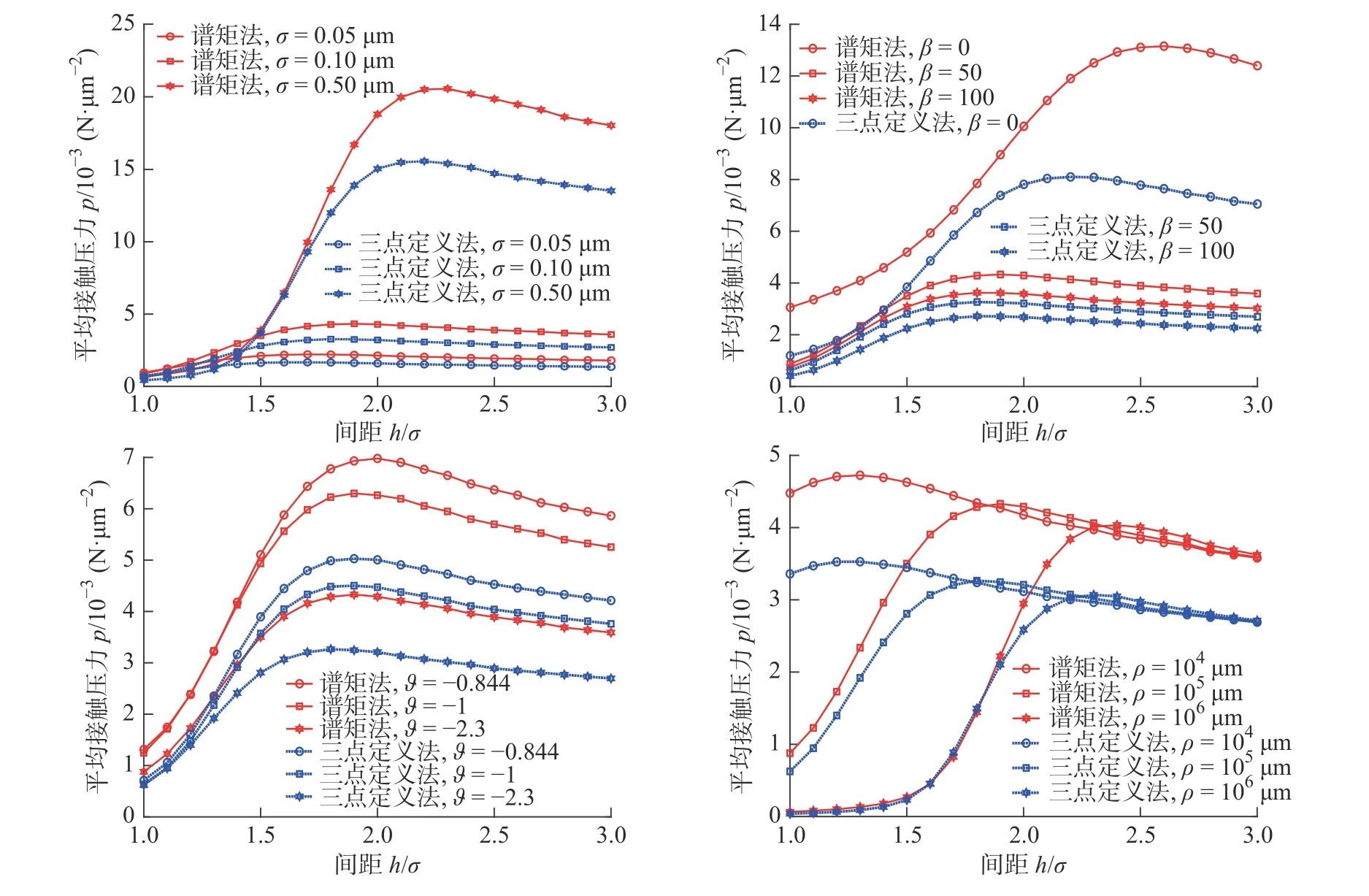
图7 不同间距h/σ 下平均接触压力求解对比Fig.7 Comparison of average contact pressure solutions at different gaps h/σ

不同相关长度、高通滤波常数和曲率半径下接触载荷P随间距d/σ和间距h/σ变化示于图8。给定间距d/σ下，谱矩法预测接触刚度小于三点定义法，且该预测偏差随标准偏差、相关长度和曲率半径增大而增大，随高通滤波常数的变化为：-1>-0.844>-2。然而，当考虑微凸体平均高度的计算差别后，相同间距h/σ下，谱矩法预测的接触刚度大于三点定义法，且该预测偏差也随标准偏差和曲率半径增大而增大，随相关长度增大而减小。

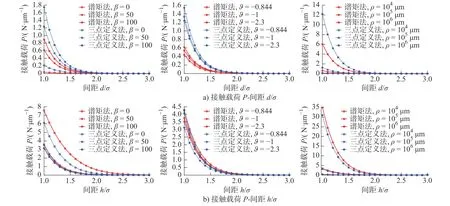
图8 接触载荷-间距关系对比Fig.8 Comparison of the relationship between contact load and spacing

2.2 接触预测偏差原因解析

为解释三点定义法和谱矩法之间的接触预测偏差，分别基于两种方法对仿真的粗糙表面随机样本计算其微凸体峰点分布参数，得到峰点高度概率密度分布和峰点曲率分布对比见图9，且图中还给出了基于实测数据的计算验证。其中，3个测试样本由M7130平面磨床、氧化铝砂轮磨削45钢工件所得，所用砂轮型号为WA46L，砂轮线速度为26 m/s，工作台进给速度0.069 m/s，进给深度为5～20 μm。所用测试仪器为Taylor Hobson 粗糙度测试仪。理论计算表明，谱矩法高估了峰点高度分布均值和峰点曲率，低估了峰点高度分布标准偏差，这与试验数据的计算结果相一致。试验与理论计算结果之间存在的差别，主要源于实测表面轮廓与所假定高斯、幂指数衰减型自相关分布之间存在一定差异。

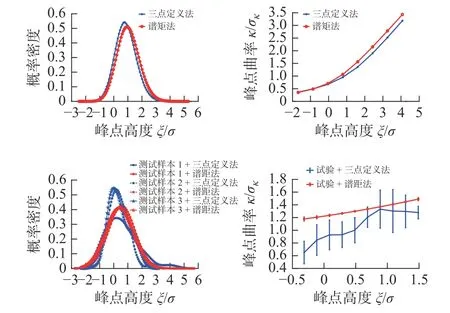
图9 微凸体峰点分布计算对比与试验验证Fig.9 Comparison and experimental validation of microasperity peak distribution calculations

三点定义法和谱矩法计算所得峰点密度对比见图10。可以显见，谱矩法低估了峰点密度。鉴于微凸体密度和曲率半径对接触求解影响很大，谱矩法对两者计算都偏小，使得其预测的接触面积都小于三点定义法。与此同时，由于计算所得微凸体高度分布标准偏差也偏小，导致相同载荷P或相同间距d/σ下，谱矩法预测的接触载荷、接触半宽和接触微凸体数亦小于三点定义法。然而，谱矩法高估了微凸体平均高度ξavg，从式（19）可知，相同间距h/σ下所得间距d/σ减小，这将导致更多的微凸体参与接触，使得谱矩法预测的接触载荷、接触半宽和接触微凸体数增多，以致大于三点定义法的计算值。不过，大多数条件下，如同图3和表1显示的那样，两种方法接触预测相对偏差在20%～30%之间。减小载荷、增大标准偏差有利于减小谱矩法的接触预测偏差，但减幅不大。

表1 接触面积预测相对偏差Tab.1 Relative deviation in predicted contact area

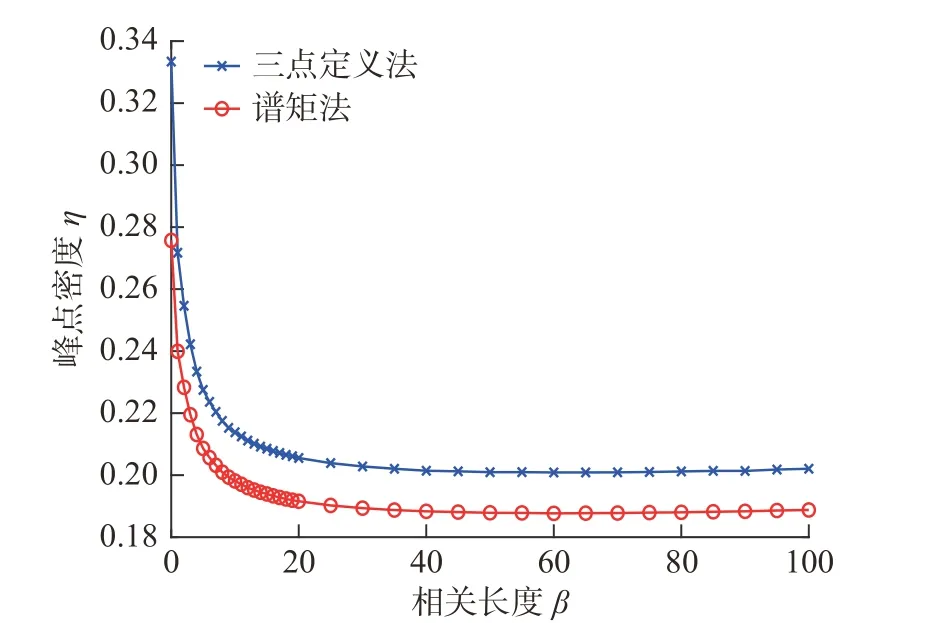
图10 微凸体峰点密度对比Fig.10 Comparison of microasperity peak densities

考虑到谱矩法应用简明，所得平均接触压力大于三点定义法，在校核接触强度时更为保守，因此适用于计算精度要求不高的接触估算，特别是对于给定载荷P下接触范围的评估，与三点定义法相差无几。需强调的是，在相同载荷P或间距d下，谱矩法预测的接触刚度小于三点定义法，但在相同间距h下，谱矩法预测的接触刚度更大。为更加准确预测接触性能，建议基于微凸体识别策略，由参数定义法来计算微凸体分布。为弱化采样间隔的不利影响，需要考虑载荷大小和材料强度对粗糙表面进行拟合预处理[2]，以提高微凸体分布参数计算的稳定性，这已超出本文研究范围，此处不再展开讨论。

3 结论

1）谱矩法高估了峰点平均高度和曲率、低估了峰点高度分布标准偏差和密度，是导致谱矩法和三点定义法接触预测偏差的原因，该偏差大小与是否考虑微凸体平均高度有较大关系，并取决于载荷水平、粗糙表面标准偏差与相关长度、高通滤波常数和曲面曲率半径。

2）所有计算条件下，谱矩法所得平均接触压力均大于三点定义法，其预测接触强度偏于保守。在相同载荷P或间距d/σ下，谱矩法预测接触刚度小于三点定义法，但考虑微凸体平均高度之后，由于高估了峰点平均高度，使得相同间距h/σ下谱矩法实际间距d/σ更小，因此其预测接触刚度偏大。在相同载荷P下，谱矩法与三点定义法预测的接触范围近乎一致。

3）谱矩法相对三点定义法的接触预测偏差一般在20%～30%之间，减小载荷、增大标准偏差可小幅减小其接触预测偏差。为准确预测接触性能，建议基于微凸体识别策略、由参数定义法来计算微凸体分布，并适当对粗糙表面进行拟合预处理。