盾构渣土改良效果评价机器人搅拌探头选型分析

王祥祥, 鞠翔宇, 2, *, 荆留杰, 杨 晨, 游宇嵩

(1. 中铁工程装备集团有限公司, 河南 郑州 450016; 2. 山东大学机械工程学院, 山东 济南 250061)

0 引言

近年来,随着我国基础设施建设的快速发展,盾构技术在推动地铁快速建设方面发挥了重要作用[1]。目前,主流的盾构类型包括土压平衡盾构和泥水平衡盾构。其中,渣土作为土压平衡盾构压力平衡的媒介,一方面可以平衡前方掌子面的水土压力,防止土体失稳;另一方面可以平衡螺机压力,保证设备顺利出渣[2]。因此,往往需要通过渣土改良使渣土具有良好的流动性、合适的塑性、较低的抗剪强度和黏附强度、较小的渗透系数和一定的压缩性[3-7],从而便于排土和控制土舱压力,降低刀盘结泥饼、刀具磨损、螺机喷涌的风险[8]。

近年来,国内外学者对渣土塑流性的测试方法与评价指标进行了大量的研究。Zumsteg等[9]与Peila等[10]通过研究发现,黏性渣土中加入泡沫后,其坍落度值明显增加,渣土塑流性增强。闫鑫等[11]发现当泡沫注入比相同时,砂土含水率低于某值可增加土颗粒间黏聚力,过量水会降低颗粒间黏聚力,导致坍落度增大。叶新宇[12]拟合大量坍落度试验数据,指出泥质粉砂岩地层盾构渣土的坍落度值与泡沫注入比和含水率呈二次函数关系。王树英等[8]针对改良后渣土理想坍落度取值范围进行了广泛调研,发现国内外对其的取值范围尚未统一,且差别较大。李培楠等[13]提出使用水泥胶砂流动度测定仪与稠度仪评价黏性渣土的塑流性,并将试验结果得到的最佳配比应用到上海某地铁盾构隧道施工中,取得了良好的施工效果。Oliveira等[14]对水泥胶砂流动度仪的试验方法进行了改进,使用渣土在玻璃板上方上下震动40次后的直径变化率F40作为渣土塑流性的评价指标,但由于数据量有限,且影响因素较多,作者未给出理想渣土的F40值。Milligan[3]与Maidl等[7]用黏稠指数来表征黏土的黏稠状态,进而评价其塑流性,得出稠度指数在0.4～0.75区间的渣土具有较好的塑流性,能够较好地满足盾构排土的要求。李培楠等[13]和Langmaack[15]采用砂浆稠度仪测定渣土的塑流性,结果表明随着改良剂掺入比的增加,圆锥的插入深度越大,渣土的塑流性越好。Quebaud等[16]与刘大鹏[17]在室内砂浆搅拌机的基础上增加了功率表,测定搅拌渣土时消耗的能量,并将能量消耗减小量作为渣土塑流性的评价指标。Mori等[18]研制了一套可以测定在一定压力下渣土抗剪强度的十字剪切试验装置,用于检测不同改良参数下的最大转矩值,以此计算改良土样的抗剪强度。Avunduk等[19]提出了一种可手持便捷式扭转剪切试验装置,并通过试验验证其测量结果与经典剪切试验具有很强的相关性,该装置能够快速简便地评价渣土的改良效果。以上研究在一定程度上降低了土压平衡盾构的施工风险,增加了盾构掘进效率,但是不同学者使用的试验仪器和评价指标各不相同,目前缺乏统一的评价标准;此外,由于缺乏盾构智能化方面的深入研究与工程实践,盾构掘进过程中渣土改良状态信息获取滞后,决策控制依赖人为经验致使盾构盲目掘进,导致渣土改良策略与地层条件不适应、掘进效率低等问题一直存在[8]。

因此,有必要研发一款室内渣土改良标准量化试验台,用于改良规律挖掘与评价指标体系的建立;与一款盾构渣土改良效果评价机器人,用于渣土实时取样与检测,并结合掘进参数,指导改良参数的快速调整。机器人与试验台皆通过安装在其上的搅拌装置搅拌渣土,检测搅拌探头插入渣土时的贯入阻力以及探头旋转时的转矩,从而评价渣土的塑流性。搅拌探头作为机器人与试验台中直接与渣土接触的装置,其形状决定了所测贯入阻力与转矩的敏感性。国内外学者对不同搅拌探头的测量效果进行了一定的探索。Li等[20]使用十字形搅拌探头测量了气压加载条件下不同贯入深度时改良砂土的搅拌转矩; Mario等[21]采用球形搅拌探头(带有球测量系统的流变仪)研究了泡沫改良土的流变特性,得到改良土剪切应力-剪切速率关系; Wan等[22]采用圆盘形探头进行了切向黏附试验,探索改良土与圆盘探头之间的黏附强度和转矩变化关系。以上研究为不同学者分别针对单一形状搅拌探头进行的试验,未对不同形状探头的测量效果进行对比分析。Hu等[23]使用CFD方法对3种不同形状探头进行仿真,对比转矩测量效果,但未对探头贯入阻力进行研究。

综上所述,本文将渣土看作非牛顿流体,通过平滑粒子流体动力学(smoothed particle hydrodynamics,SPH)方法对不同形状搅拌探头贯入渣土以及搅拌过程进行仿真,并在仿真结果的基础上利用层次分析法对不同形状搅拌探头测量的搅拌转矩与贯入阻力敏感性进行分析,以期为机器人与试验台的研发应用提供帮助。

1 SPH理论与渣土流变特性

1.1 SPH基本理论

平滑粒子流体动力学是一种无网格或自由网格的数值方法,其不需要定义有限元通常定义的节点和单元,只需用一个点集合代表一个给定物体,SPH中定义的点通常指粒子或虚拟粒子。

SPH法的核心实为一种插值,宏观物理变量(密度、压力、温度)f(x)能非常方便地借助于一组无序点上的值表示成积分插值计算得到,其方程的构造涉及2个关键问题[24-25]： 函数的光滑近似逼近、质点的近似逼近。

1.1.1 函数的光滑近似逼近

应用积分表示函数的核近似法对任意函数和光滑核函数进行逐步积分如下:

(1)

式中:f(x)为任意空间变量的函数;D为x的积分区间;W(x-x′,h)为光滑函数,又被称作插值函数;h为定义光滑函数的影响区域的光滑长度。

1.1.2 质点的近似逼近

在SPH方法中,整个系统是由具有独立的质量、占有独立空间的有限个粒子表示的。应用粒子近似法可让与核近似法相关的连续积分表示式转化为支持域内所有粒子叠加求和的离散化形式[26]：

(2)

式中:mi、ρi分别为粒子的质量和密度;i为计算质点记号;N为质点总数。

通过式(1)和式(2)便可对任意函数f(x)在空间坐标内进行SPH方法的离散化处理。转化后的不可压缩流体的Navier-Stokes公式的形式如下。

质量守恒方程为:

(3)

动量守恒方程为:

(4)

能量守恒方程为:

(5)

式(3)—(5)中:v为速度;e为热能;σ为应力张量;P为压力;μ为动力黏滞系数;ε为动剪应变率;α和β代表不同坐标方向;i和j代表不同质点,其中i为计算质点记号,j为邻近质点记号。

SPH方法可以像其他拉格朗日模型那样指定初始条件与边界条件,也允许与其他拉格朗日体的接触相互作用。在变形并非很严重时,SPH方法的精度比拉格朗日有限元分析要低,但是在诸如液体晃动、波浪工程等大变形仿真的应用上具有很高的精度[27]。搅拌探头贯入与旋转的过程中,渣土发生极大变形,因此SPH方法适用于该工况。

1.2 渣土流变特性

由坍落度试验可知,渣土在自重作用下缓慢流动塌落并最终达到某一稳定高度,表明当剪切应力大于屈服应力时,渣土似流体般发生剪切流动;当剪切应力小于屈服应力时,渣土似固体般不发生变形[28],其剪应变率与剪应力之间呈非线性关系,可采用非牛顿流体模型中的Bingham流体模型对此进行描述,如式(6)所示。

τ=τ0+μpγ。

(6)

式中:τ0为动切应力(简称动切力或初始屈服应力),Pa;μp为塑性黏度,Pa·s;τ为剪切应力,Pa;γ为剪切速率,s-1。

2 SPH数值模拟方案

2.1 数值模型

搅拌探头选用S1、P1、B1、B2、C2 5种型号,搅拌探头的搅拌直径均为94 mm,如图1所示。渣桶底部半径75 mm,顶部半径100 mm,渣土在桶内的高度为145 mm,如图2所示。每个搅拌探头划分为约3 000个四面体网格,单元类型均为C3D10M; 渣桶划分为5 858个四边形网格,单元类型为S4R; 渣土划分为31 764个六面体网格,单元类型为C3D8R,计算过程中C3D8R单元转化为粒子。

图1 搅拌探头

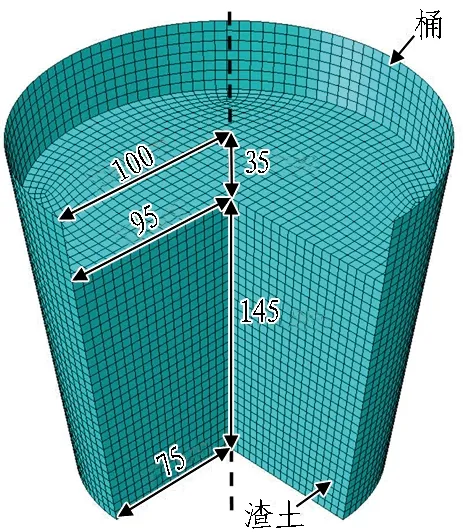
图2 桶与渣土(单位: mm)

2.2 边界条件

建立几何模型时,以Y方向作为竖向,以X、Z方向作为水平方向。在分析过程中始终限制渣桶X、Y、Z3个方向上的位移与旋转自由度,使其完全固定。对于搅拌探头,初始时限制X、Z方向上的位移自由度与X、Y、Z3个方向上的旋转自由度,分析时限制X、Z方向上的位移与旋转自由度,Y方向(竖向)的位移设定为-150 mm,旋转速度设定为60 r/min,方向为逆时针旋转。

为了模拟机器人和试验台搅拌探头贯入、搅拌的工况,使用幅值曲线控制探头位移与转速的施加。搅拌探头位移与转速施加时机及变化情况如图3所示。在0～0.5 s,搅拌探头位移沿竖向线性增加,0.5 s达到最大位移150 mm后停止贯入,从而模拟搅拌探头贯入渣土的过程; 在0.5～1 s,搅拌探头旋转速度由0 rad/s线性增加至6.28 rad/s; 在1～4 s,搅拌探头保持6.28 rad/s逆时针匀速旋转,从而模拟渣土搅拌切割的过程。

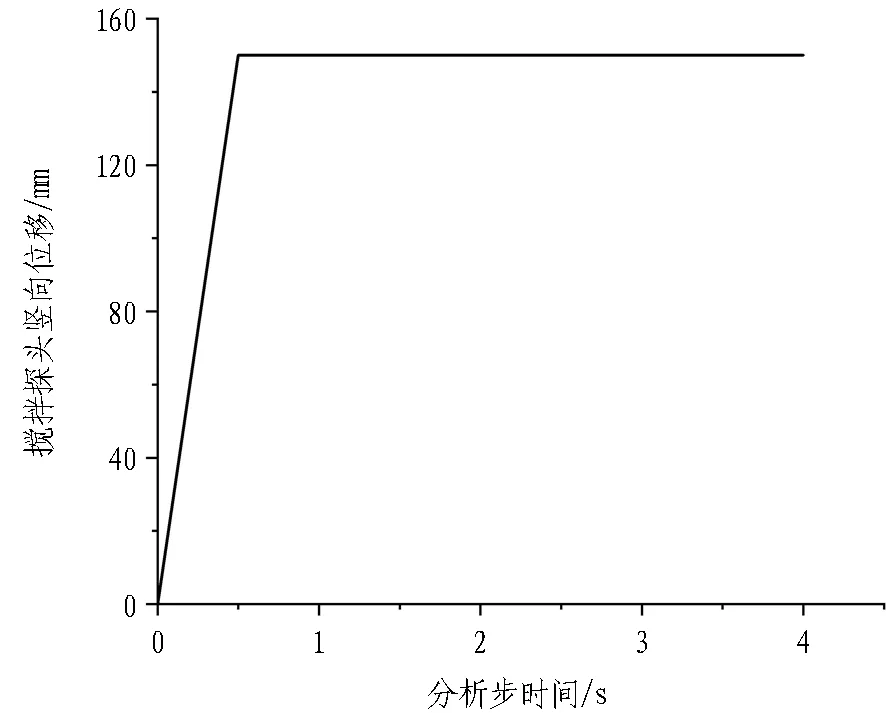
(a) 搅拌探头竖向位移(b) 搅拌探头转速

图3 搅拌探头位移与转速施加时机及变化情况

Fig. 3 Application timing, changes of displacement, and speed of mixing probe

2.3 材料参数设置

搅拌探头与渣桶为钢材质,由于计算过程中搅拌探头与搅拌桶受力较小,不会发生塑性变形,所以将其视为线弹性材料。使用Bingham模型表达渣土的流变特性。为了得到搅拌探头在不同强度渣土中的转矩与贯入阻力的变化规律,参考文献[23,29]中渣土实测流变参数,将初始屈服应力分别设定为10、50、150、250、350 Pa,将黏度设定为100、200、300、400 Pa·s,并进行正交仿真试验。渣土流变参数见表1。

3 仿真结果分析

3.1 搅拌转矩与贯入阻力时变曲线分析

以60 r/min转速的S1型搅拌探头,初始屈服应力10 Pa、黏度300 Pa·s的渣土为例,如图4所示,搅拌转矩与贯入阻力时变曲线可以划分为4个阶段。

表1 渣土流变参数[23,29]

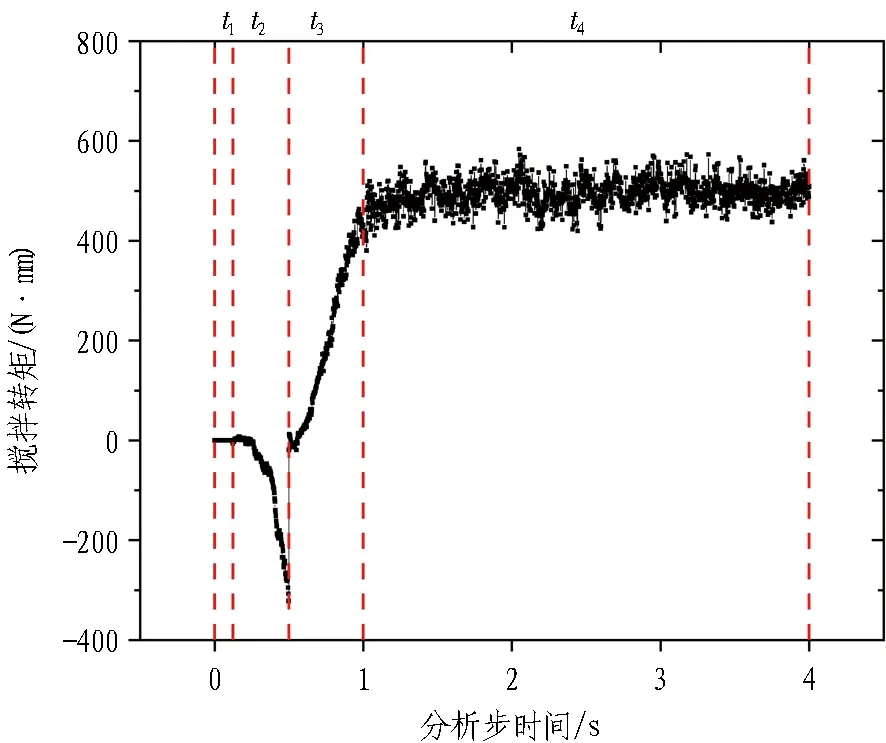
(a) 搅拌转矩随时间变化曲线

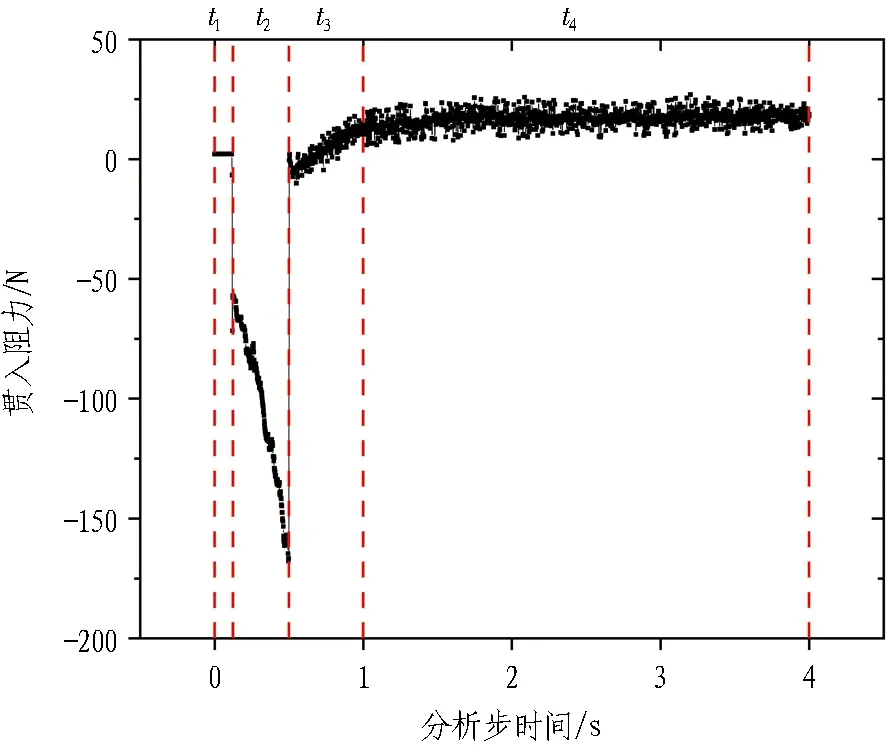
(b) 贯入阻力随时间变化曲线(“-”表示受压,“+”表示受拉)

3.1.1t1段: 0～0.12 s

搅拌探头匀速向下运动,但还未接触到渣土表面。此时搅拌探头转矩与贯入阻力皆为0。

3.1.2t2段: 0.12～0.5 s

搅拌探头接触到渣土表面后继续匀速向下运动。如图5(a)所示,在搅拌探头贯入过程中,受到渣土对其竖直向上的阻力F1y,为了保持匀速向下运动,搅拌探头同时受到方向竖直向下、大小与渣土阻力相同的力,这是一对作用力与反作用力。因此,搅拌探头受压,受力为负,如图4所示。

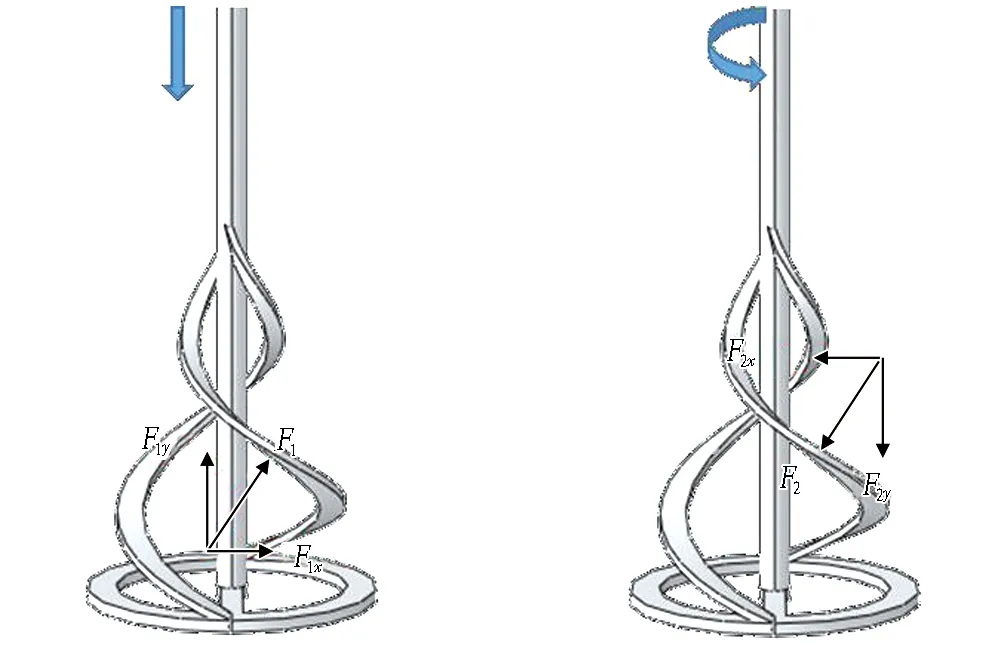
图5 搅拌探头受渣土作用力分析

根据搅拌探头贯入阻力随时间变化曲线可知,当搅拌探头接触到渣土表面瞬间,所受贯入阻力猛然增大,然后随着贯入深度的增加逐渐增大,直到0.5 s瞬时,搅拌探头停止贯入时达到峰值,并迅速变为小于0的负值。之所以出现小于0的负值,是由于0.5 s瞬时,搅拌探头还未开始转动,此时搅拌探头受到渣土竖直向上的浮力,为了克服浮力保持静止,搅拌探头同时受到竖直向下的反作用力。

根据搅拌探头转矩随时间变化曲线可知,在搅拌探头向下贯入过程中受到渣土对其的反向转矩,并随着贯入深度的增加不断增大。由图5可知,这是由于在向下贯入时搅拌探头受到水平向右的分力F1x,在逆时针旋转时搅拌探头受到水平向左的分力F2x,2种状态下搅拌探头所受的水平分力方向相反,因此在向下贯入时产生相对逆时针旋转时的反向转矩。

3.1.3t3段: 0.5～1 s

搅拌探头停止贯入,保持竖向的静止,转速开始均匀增加。搅拌探头旋转时,渣土对搅拌探头存在竖直向下的分力F2y,为了保持竖向静止,搅拌探头同时受到竖直向上的反作用力,此时,搅拌探头受拉,受力为正。随着转速的不断增大,该反作用力不断增大最终保持稳定; 随着转速的匀速增加,转矩不断增大,最终保持稳定。

3.1.4t4段: 1～4 s

搅拌探头保持匀速旋转,搅拌探头转矩与受力保持稳定。

3.2 流变参数对搅拌转矩与贯入阻力影响分析

以B2型搅拌探头为例,提取不同流变参数条件下搅拌探头的贯入阻力峰值与搅拌转矩平稳值进行分析,如图6和图7所示。由图可知,随着渣土黏度与初始屈服应力的增大,搅拌转矩与贯入阻力均呈线性增加的趋势。但是与黏度相比,初始屈服应力对搅拌转矩与贯入阻力的影响相对较小。

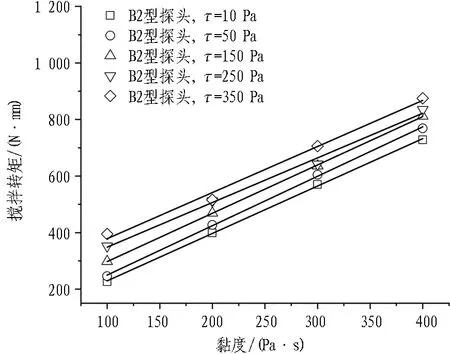
(a) 黏度对搅拌转矩的影响

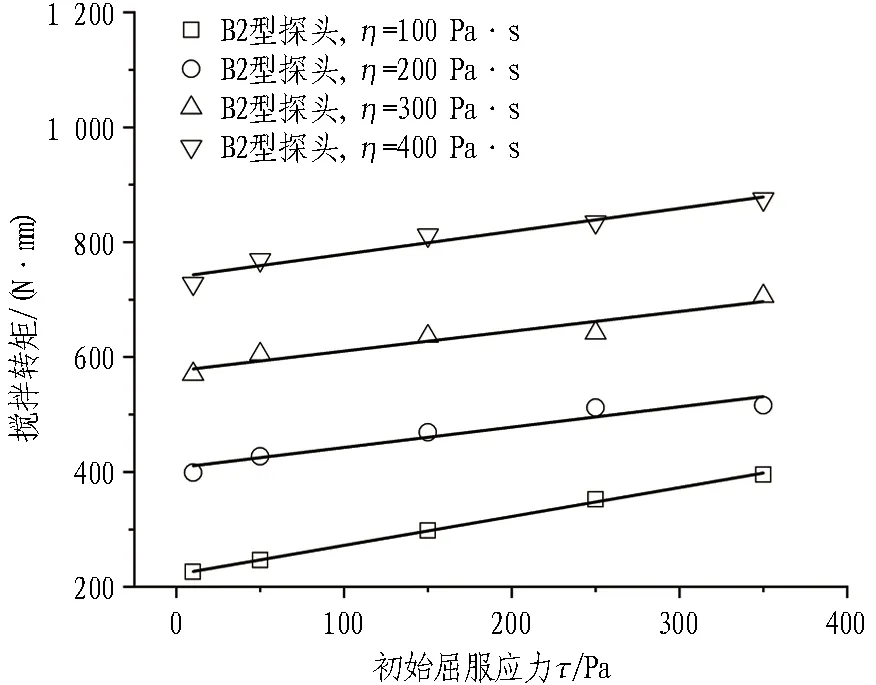
(b) 初始屈服应力对搅拌转矩的影响

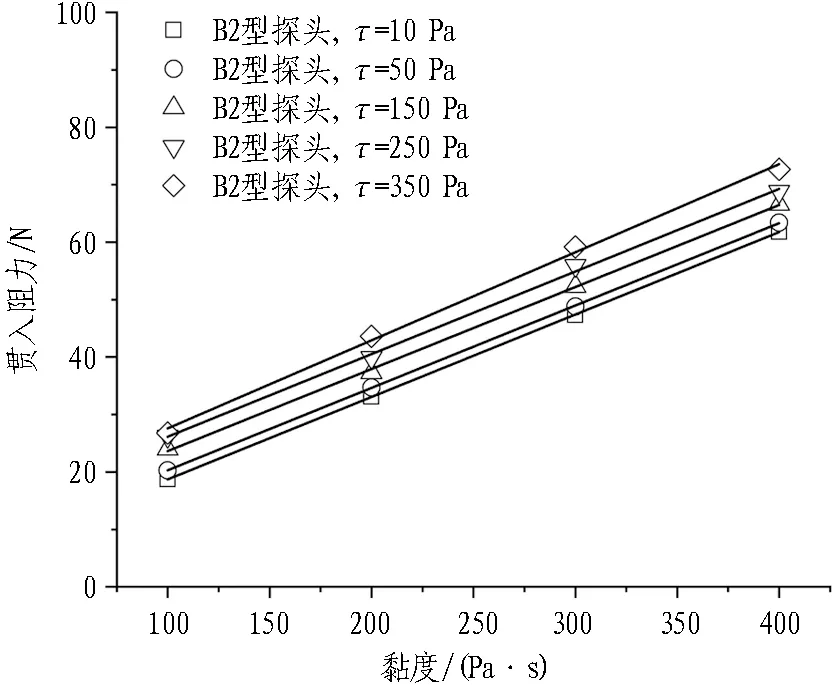
(a) 黏度对贯入阻力的影响

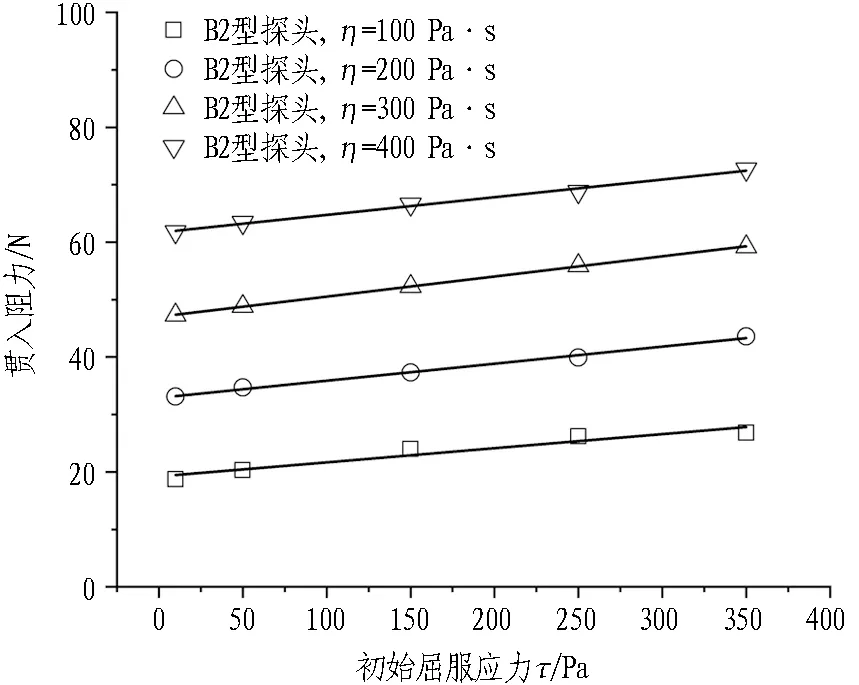
(b) 初始屈服应力对贯入阻力的影响

3.3 搅拌探头对搅拌转矩与贯入阻力的影响分析

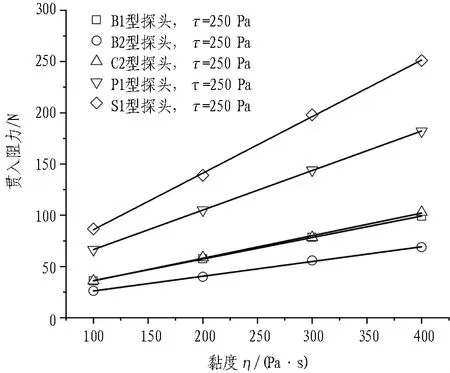
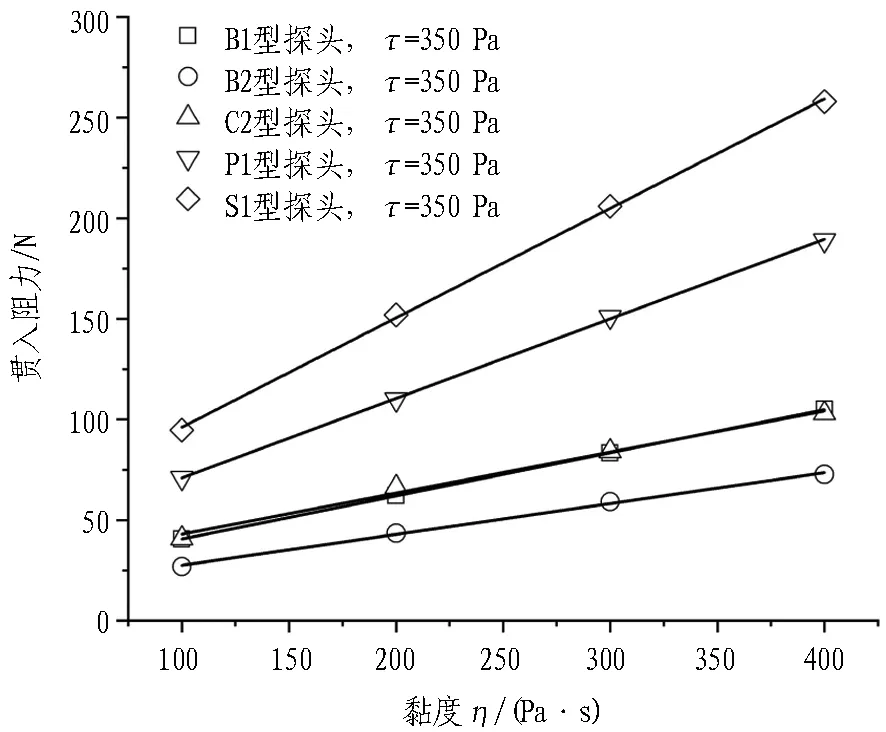
图8和图9示出初始屈服应力τ一定时,不同型号搅拌探头的搅拌转矩与贯入阻力随黏度η的变化曲线。由图可知,对于不同型号的搅拌探头,其搅拌转矩与贯入阻力均随黏度η的增大而线性增大,但是不同型号搅拌探头的搅拌转矩与贯入阻力随黏度变化曲线的斜率存在明显的差别,这说明不同的搅拌探头对于搅拌转矩与贯入阻力的“敏感度”不同,曲线的斜率越大,说明搅拌探头对于所测数据越“敏感”。

对不同型号搅拌探头的搅拌转矩与贯入阻力随黏度变化曲线进行线性拟合,得到拟合曲线的斜率如表2所示。通过对比曲线的斜率不难发现: 搅拌转矩敏感度C2>B1>B2>P1>S1,而贯入阻力敏感度S1>P1>C2>B1>B2。

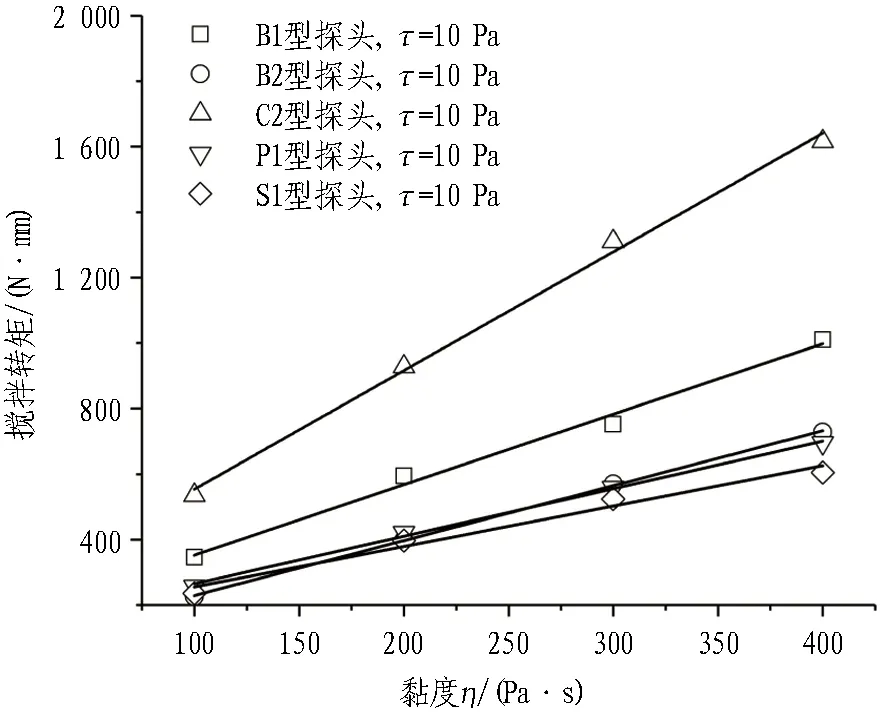
(a) τ=10 Pa

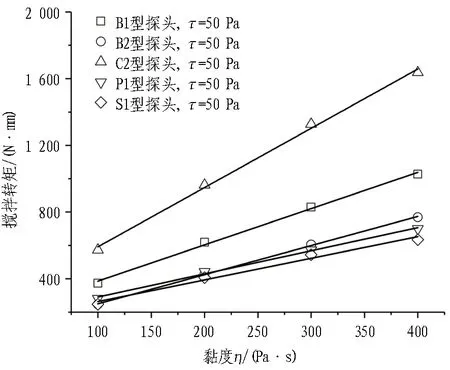
(b) τ=50 Pa

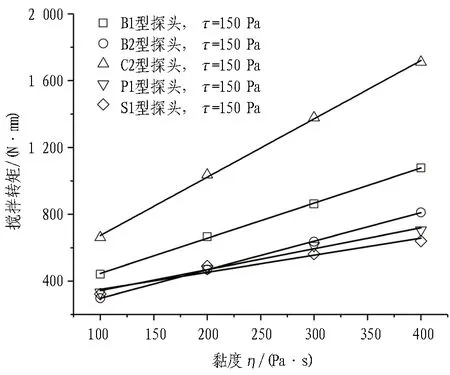
(c) τ=150 Pa

(d) τ=250 Pa

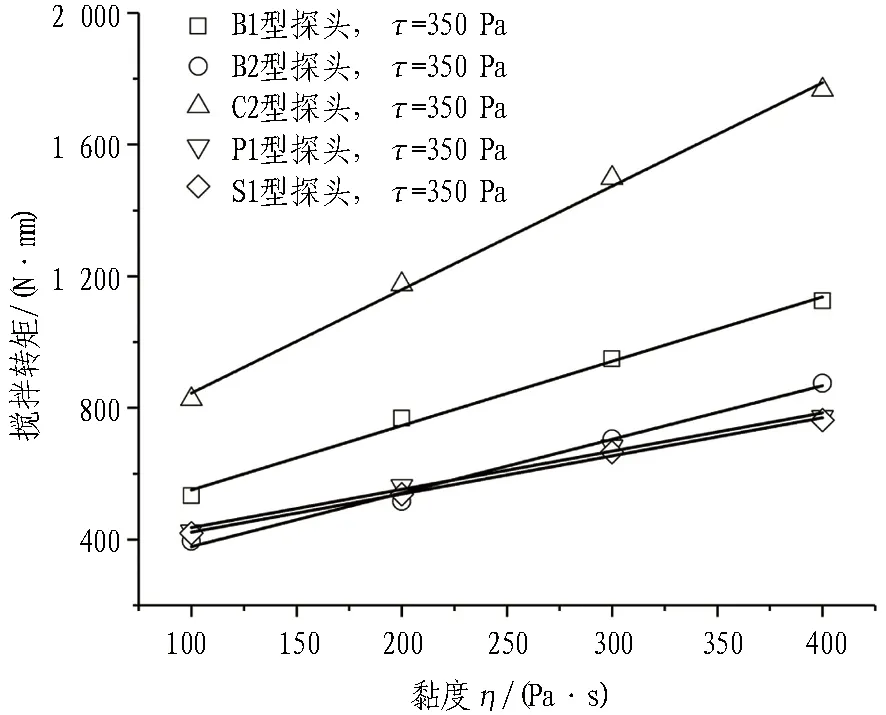
(e) τ=350 Pa

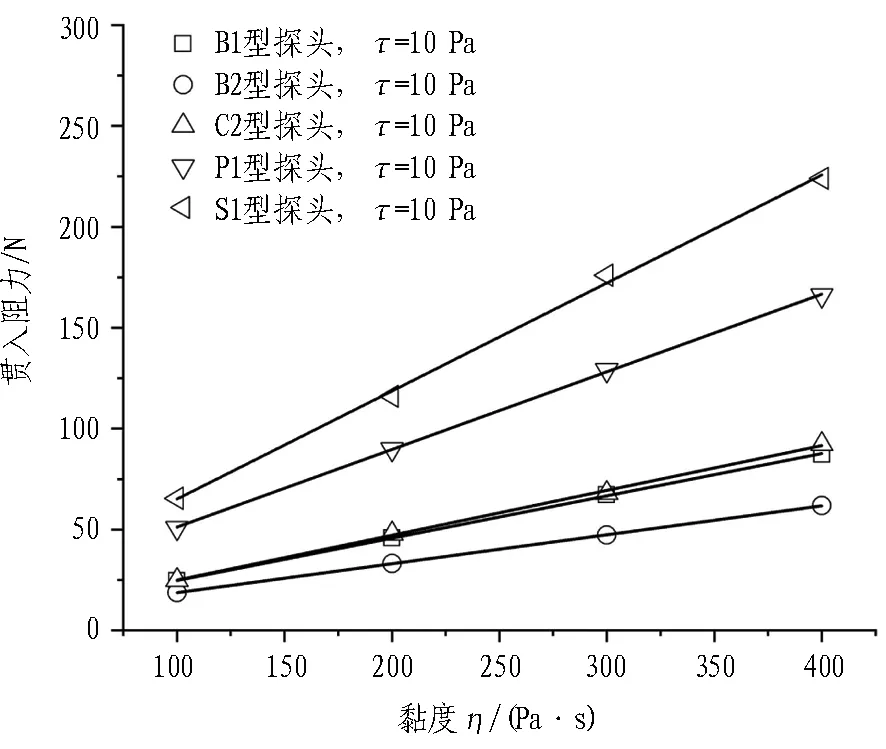
(a) τ=10 Pa

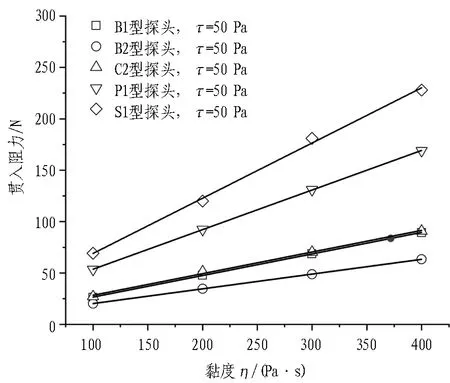
(b) τ=50 Pa

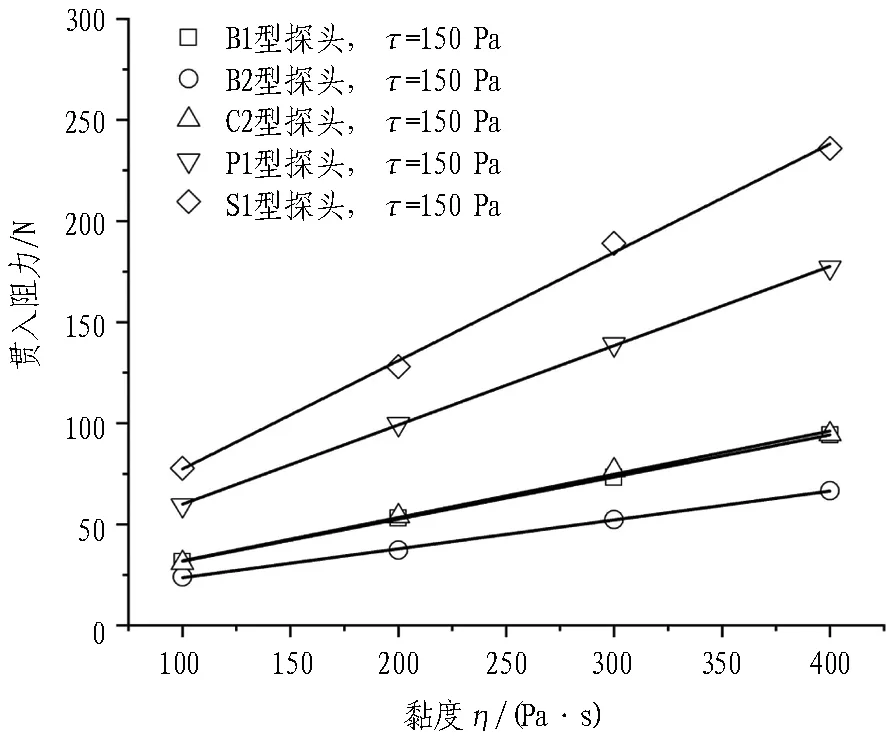
(c) τ=150 Pa

(d) τ=250 Pa

(e) τ=350 Pa

4 基于层次分析法的搅拌探头选型分析

4.1 层次分析法

层次分析法(analytic hierarchy process,AHP)是一种定性和定量相结合、系统化、层次化的分析方法。层次分析法的基本步骤包括: 1) 建立层次结构模型; 2) 构造成对比较矩阵; 3) 计算权向量并做一致性检验; 4) 计算组合权向量。

对于搅拌探头选型而言,首先,对5个型号的搅拌探头按照搅拌转矩、贯入阻力2个选型标准构建层次结构模型; 其次,分别构造搅拌转矩与贯入阻力的对比矩阵,计算权重向量并做一致性检验; 然后,构造单因素条件下不同搅拌探头敏感性对比矩阵,并分别计算权向量; 最后,计算组合权向量并对搅拌探头进行排名。

4.2 影响搅拌探头选型的各因素权重计算

4.2.1 构造相对重要性矩阵

影响搅拌探头选型的主要因素是搅拌转矩与贯入阻力,但是考虑到检测时间、检测数据连续性、抵抗检测环境影响能力等因素,对于搅拌探头来说搅拌转矩的重要性要大于贯入阻力。结合表3和表4,假设搅拌转矩的重要性比贯入阻力略大,通过两两对比,得到相对重要性矩阵A。

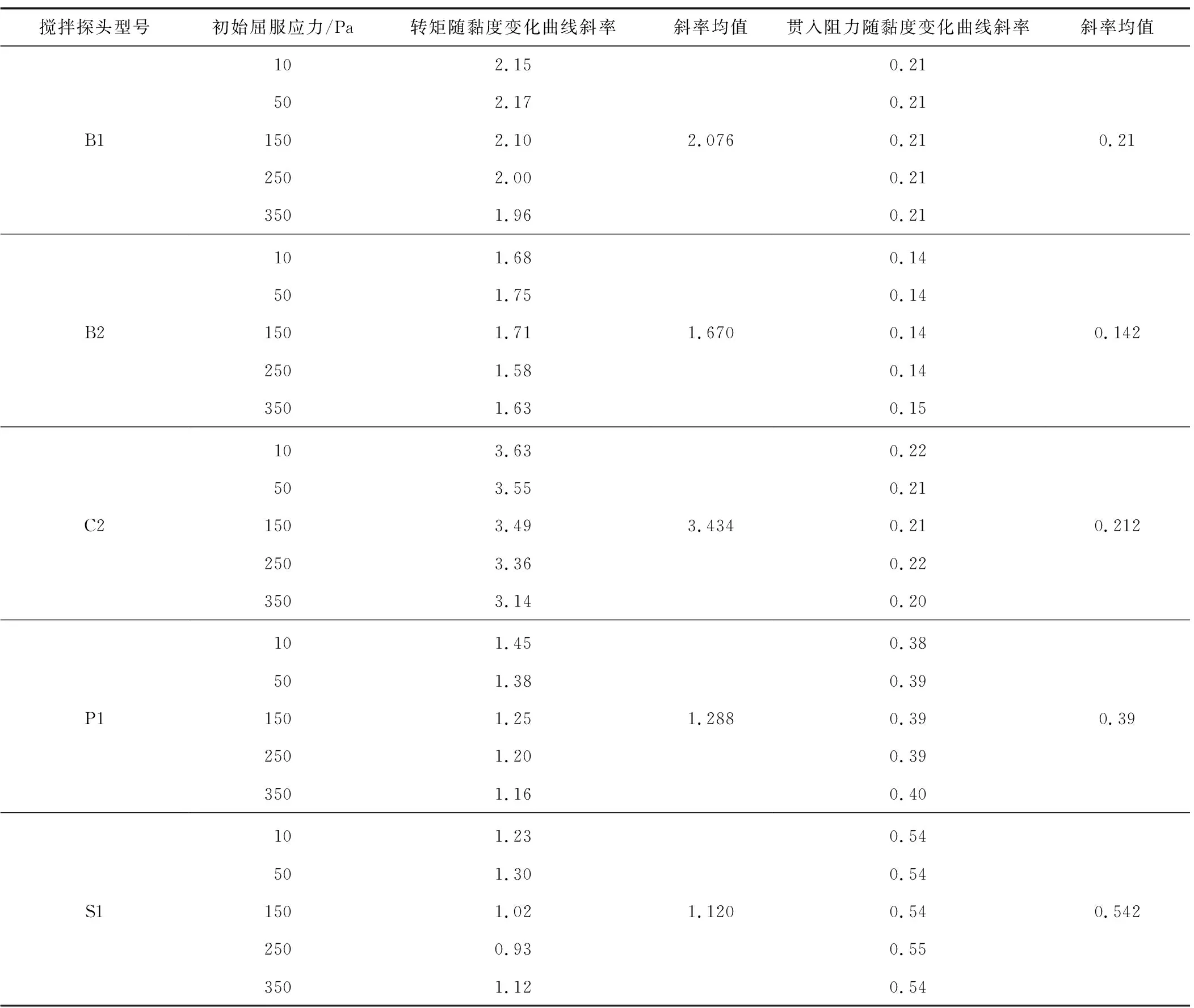
表2 不同型号搅拌探头转矩与贯入阻力随黏度变化曲线斜率

表3 风险权重评价分值表

表4 搅拌转矩与贯入阻力两两对比结果

4.2.2 计算矩阵的特征值与特征向量

通过计算矩阵A的最大特征值λmax(A)=2; 最大特征值对应的特征向量β=(0.948 683 3,0.316 227 77)T。

3) 计算随机一致性比率,判断矩阵是否具有满意的一致性。

不一致程度的指标

(7)

式中n为矩阵的阶数。

4.2.3 特征向量的归一化

将特征向量β归一化后得到β1=(0.75,0.25)T,因此得到搅拌转矩的权重值为0.75,贯入阻力的权重值为0.25。

4.3 单因素条件下不同搅拌探头敏感性权重计算

4.3.1 各搅拌探头搅拌转矩敏感性权重计算

转矩随黏度变化曲线斜率是评价搅拌探头转矩敏感度的重要标准。因此,以表5中的斜率为两两对比的依据,构造不同搅拌探头的搅拌转矩敏感性相对重要性矩阵,结合4.2节中的计算步骤与方法计算归一化的特征向量。

表5 不同搅拌探头转矩随黏度变化曲线斜率

相对重要性矩阵B的最大特征值λmax(B)=5,归一化的特征向量β2=(0.217,0.174,0.358,0.134,0.117)T。

4.3.2 各搅拌探头贯入阻力敏感性权重计算

以表6中的斜率为两两对比的依据,构造相对重要性矩阵C,结合4.2节中的计算步骤与方法计算归一化的特征向量。

表6 不同搅拌探头贯入阻力随黏度变化曲线斜率

相对重要性矩阵C的最大特征值λmax(C)=5,归一化的特征向量β3=(0.140,0.095,0.142,0.261,0.362)T。

4.4 选型结果

根据4.2、4.3节的计算结果可知: 搅拌转矩与贯入阻力对影响搅拌探头选型的权向量β1=(0.75,0.25)T; 各搅拌探头的搅拌转矩敏感性权向量β2=(0.217,0.174,0.358,0.134,0.117)T; 各搅拌探头贯入阻力敏感性权向量β3=(0.140,0.095,0.142,0.261,0.362)T。

B1型搅拌探头的综合得分为0.75×0.217+0.25×0.140=0.198。同理,分别求出所有型号搅拌探头的综合得分如表7所示。根据搅拌探头综合评分进行排序: C2>B1>S1>P1>B2。因此,C2型搅拌探头为最佳搅拌探头。

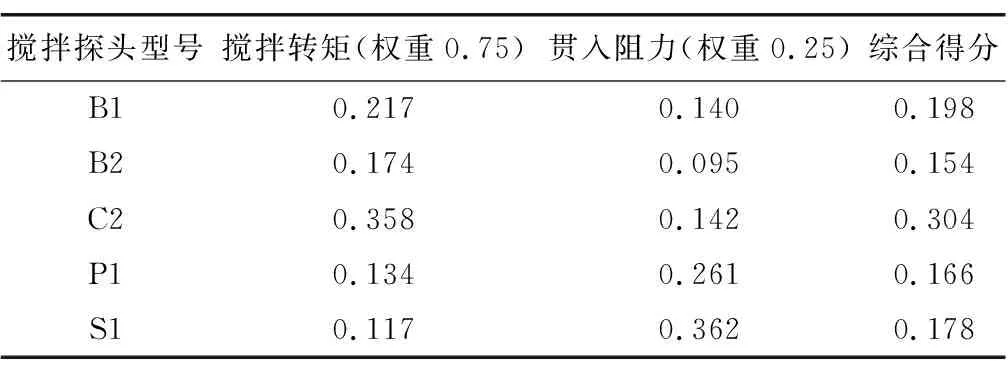
表7 各型号搅拌探头综合得分

5 选型结果验证

5.1 试验设备及材料

搅拌试验是在渣土改良标准量化试验台上完成的(见图10)。该试验台搅拌模块旋转速度为60 r/min,纵向运动模块运动速度为40 mm/s,转矩量程为±4 N·m,拉压力量程为100 N,精度为0.3%FS,可以完成对渣土的贯入、拉拔与搅拌试验,满足本试验的测试要求。

图10 渣土改良标准量化试验台

试验用土取自郑州某地铁车站施工现场,取样深度位于盾构区间所在高程范围内。经过测试,该原状土小于0.075 mm的细颗粒占总体的95%以上,塑限含水率为15%,液限含水率为25%。

5.2 试验方案

为了验证选型结果,使用易于加工制作的C2型搅拌探头与B1型搅拌探头进行试验,渣土的含水量配比与泡沫掺入比如表8所示。同时,通过3.1节的分析可知: 向下贯入时搅拌探头受压,逆时针旋转时搅拌探头受拉,受力状态发生了转变,不利于力的监测。因此,在进行试验时,搅拌探头以顺时针方向旋转,使其在竖向上一直处于受压状态。

表8 试验方案

5.3 试验结果

实测搅拌转矩随时间变化曲线如图11所示。由图可知,当渣土含水率较低时,转矩在进入渣土初期会出现峰值,随后逐渐趋于平稳;随着渣土含水率的升高,当渣土含水率为30%时,搅拌探头进入渣土后,转矩立即进入平稳状态。实测贯入阻力时变曲线如图12所示。由图可知,在搅拌探头向下贯入过程中贯入阻力(探头所受压力)逐渐增大,直到探头停止向下移动,所测贯入阻力达到最大值; 当探头开始旋转搅拌渣土时,探头所受压力趋于稳定。

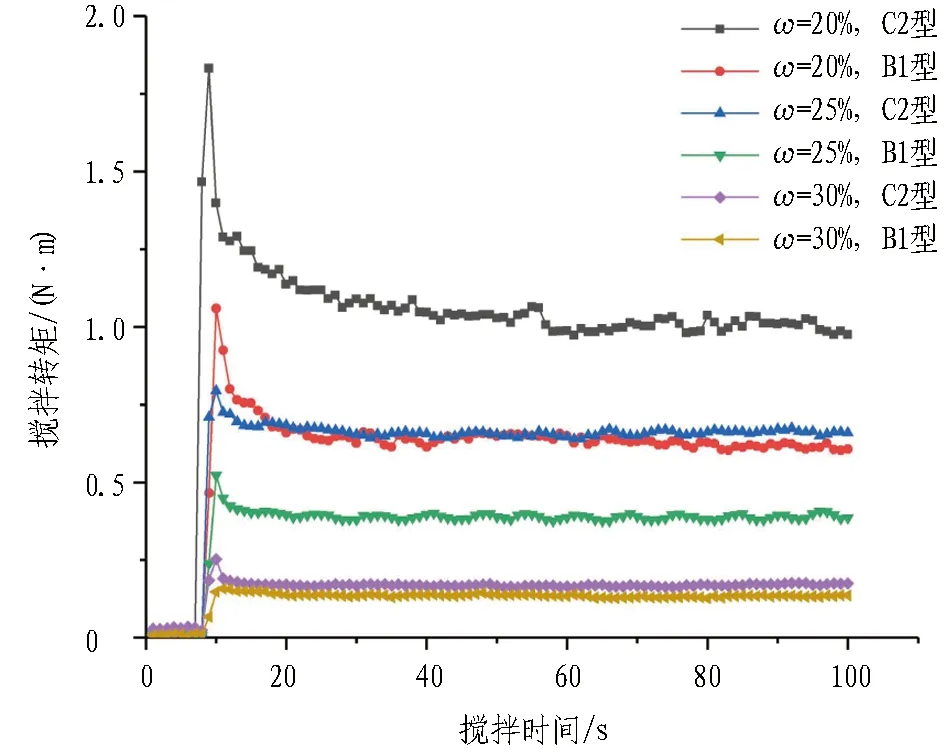
图11 实测搅拌转矩随时间变化曲线

在低围压条件下,渣土黏度随着含水率的升高而逐渐降低,且呈近似线性变化的趋势[30]。因此,取每组试验搅拌转矩平稳值与贯入阻力峰值分别绘制其随含水率的变化曲线,如图13和图14所示。可以看出,2种搅拌探头数据变化规律与数值模拟结果(见图8、图9)基本一致,可以说明选型结果的合理性。

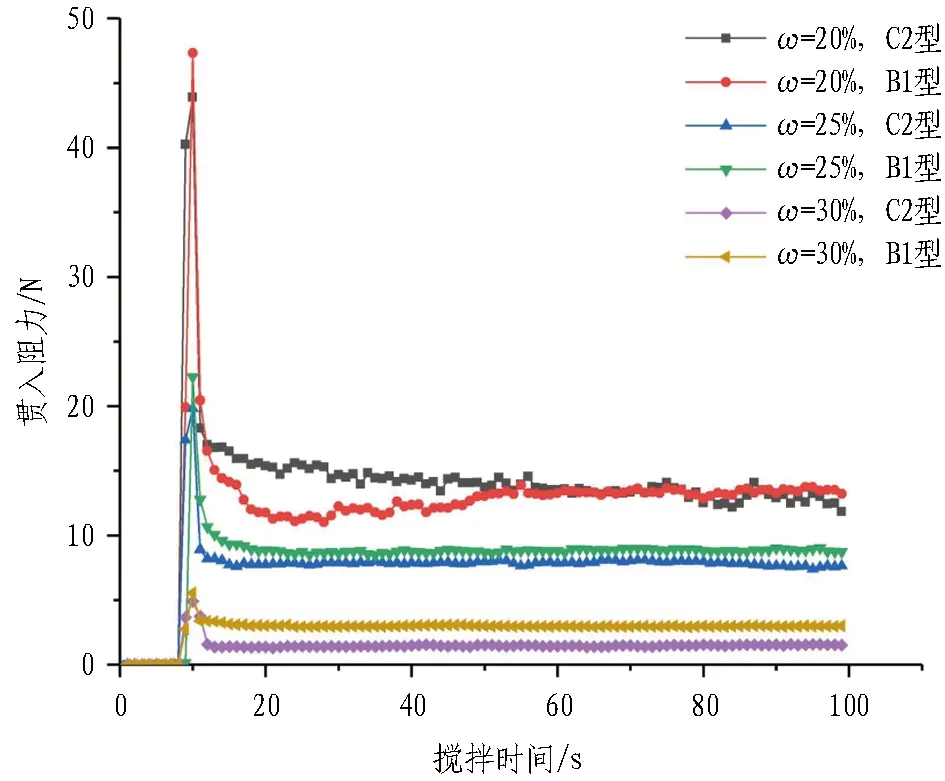
图12 实测贯入阻力时变曲线(正值表示受压)

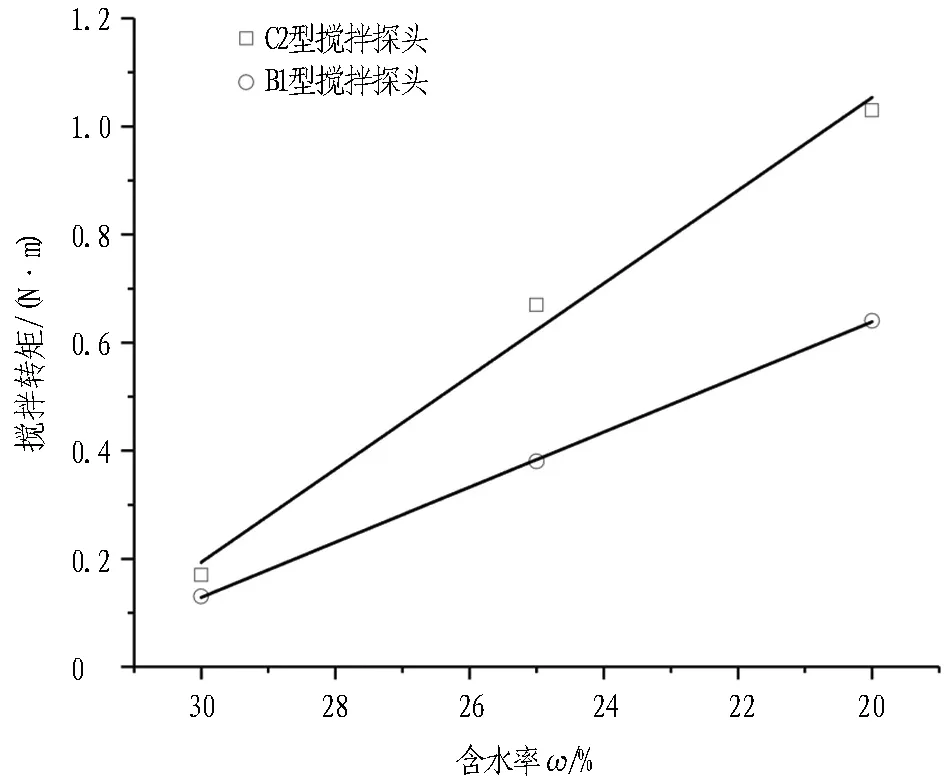
图13 不同搅拌探头搅拌转矩随含水率变化趋势

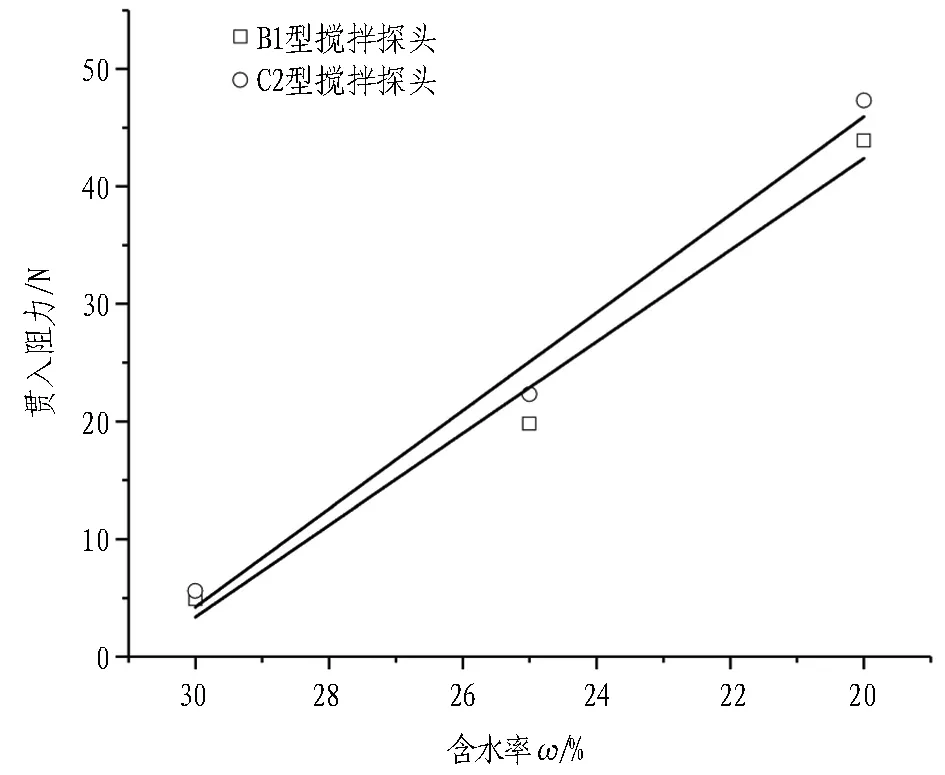
图14 不同搅拌探头贯入阻力随含水率变化趋势

6 结论与建议

搅拌探头作为机器人和试验台上唯一与渣土发生接触的部件,其对搅拌转矩与贯入阻力检测的准确性与灵敏度至关重要。因此,本文将渣土假定为宾汉姆流体,通过SPH方法对不同型号的搅拌探头贯入、搅拌渣土的过程进行动态仿真,运用层次分析法综合考虑不同搅拌探头对贯入阻力与搅拌转矩的检测灵敏度,得到如下结论:

1)根据搅拌转矩与贯入阻力时变曲线分析可知,贯入阻力随搅拌探头匀速贯入深度的增加而增加,搅拌转矩随着搅拌探头转速的增加而增加。

2)根据贯入阻力与搅拌转矩的影响因素分析可知,贯入阻力与搅拌转矩均随渣土初始屈服应力与塑性黏度的增大而增大; 并且,渣土的塑性黏度对其影响更大,对初始剪切屈服应力的影响较小。

3)C2型搅拌探头可以同时兼顾贯入阻力与搅拌转矩灵敏度要求,为本次选型的最佳搅拌探头,可用于粉质黏土地层渣土改良效果评价机器人掘进试验。

进一步地,结合本文搅拌探头的选型结果,在标准量化试验台与机器人上使用相同的搅拌探头与渣土容器,使其在相同的检测体系下分别开展室内渣土改良试验与现场搭载试验,用于探索改良规律并建立评价体系; 在此基础上,结合机器人现场检测数据与掘进参数评价当前渣土改良状态,并给出改良建议。