基于分类算法的高实时性织物疵点检测

杨晓波,白直灿

(浙江树人学院,浙江 杭州 310015)

传统人工验布速度约为10 m/min,检测效率低且易受检测人员主观因素影响。随着计算机科学和图像处理技术的不断发展,机器视觉被引入织物疵点检测,并逐渐替代人工检测。国内外专家和学者进行了深入研究,并陆续提出了许多有价值的织物疵点检测算法。Amet等[1]提出了一种子带共生矩阵方法,利用小波分解将原始图像分解为多个子带图像,并计算共生矩阵特征值,检测精度可达88%;Rosler[2]从共生矩阵中提取新的特征值检测织物疵点,检测精度可以提高到90%;邹超等[3]提出了一种模糊逻辑灰度分类方法,利用少量类别替代256个灰度级,不需要复杂的特征计算即可得到模糊类别共生矩阵,但只适用于简单素色织物。共生矩阵方法虽然检测精度较高,但存在灰度级别划分方法不统一且特征值计算量较大等问题。

Conci等[4]利用分形方法对155幅大小为256像素×256像素的织物图像样本进行检测,检测精度达到92%;Bu等[5]提取4种分形特征,对织物纹理进行分类检测,检测精度最高可达93.5%。分形方法虽提高了检测精度,但对于连续性不强且形状特征不显著的疵点难以检测。

Jain等[6]提出了一种基于Gabor滤波器组的非监督疵点分割算法,该算法采用多个滤波器组覆盖整个频域空间,可以非监督的检测疵点的位置和频率;Mak[7]采用Gabor小波网络从无疵点的织物纹理中提取最优纹理特征,并用其检测织物疵点,对平纹和斜纹的检测效率分别达到94.3%和95.2%,检测速度达到20 m/min。由于一种Gabor滤波器只能检测一种类型的疵点,而在生产现场待检测的织物疵点种类繁多,因此采用滤波器训练疵点特性不适合用于生产现场。

Cohen等[8]采用高斯马尔科夫随机场对织物纹理进行建模,经过假设检验过程检测织物疵点;Baykut等[9]将基于高斯马尔科夫随机场与基于KL变换的织物疵点检测算法进行比较,结果表明前者的计算效率高于后者。由于马尔科夫随机场只能对较大疵点反应灵敏,因此该方法不适用于对细小疵点进行检测。

上述算法中由于计算量较大,难以满足疵点实时性检测的要求,不能有效地提高检测效率,因而难以得到实际应用。基于此,本文提出一种基于分类算法的高实时性织物疵点检测方法,以达到仅对正常纹理织物进行训练后便可检测未知类型疵点,克服神经网络等传统机器学习算法需要大样本训练的问题,满足织物疵点高实时性检测要求。

1 疵点检测算法流程

采用机器学习方法可以进行奇异性检测[10],适用于解决疵点分类问题,分类器在训练过程中仅需要对正常织物样本进行训练,而不需要对疵点织物样本训练,因而节约了训练时间,比较适合在线疵点实时检测。

织物疵点的检测过程包含2个阶段:学习阶段和分类阶段。疵点检测可以认为是一个分类过程,对织物疵点的检测算法流程如图1所示。 在学习阶段,只需对正常织物纹理样本进行训练,不需要训练疵点样本,正常纹理样本可根据纹理模型进行量化,图像经过量化后便可提取纹理特征,纹理特征通常是由1组纹理特征向量构成,这些特征向量用于支持选择合适的纹理特征分类器。在分类阶段,先将待检测的织物样本进行图像量化,接着提取待测样本的纹理特征,最后利用最优的分类器进行特征分类,判别待测样本中是否含有疵点。

图1 疵点检测算法流程图Fig.1 Flowchart of defect detection algorithm

2 创建织物纹理模型

选取素色无疵点的平纹和斜纹织物样本(图2),并分析二者的灰度直方图,如图3所示。

图2 无疵点平纹和斜纹织物样本Fig.2 Samples of no-defect plain fabric(a) and twill fabric(b)

图3 无疵点平纹和斜纹织物灰度直方图Fig.3 Gray level histogram of no-defect plain fabric(a) and twill fabric(b)

通过分析2种类型织物的灰度直方图可以发现,素色平纹织物包含1个灰度色调,而素色斜纹织物则包含2个灰度色调。2种织物纹理模型近似服从由2个高斯函数组合在一起的高斯分布,因此织物的纹理模型可以采用灰度级概率密度函数来表示,平纹织物的概率密度函数如式(1)所示:

(1)

式中:μ和σ分别代表高斯分布的均值和方差。

斜纹织物的纹理模型对应灰度级概率密度函数如式(2)所示:

(2)

式中:ω1和ω2分别表示2个高斯函数的加权值,且ω1+ω2=1;μ1、σ1与μ2、σ2分别代表2个高斯函数的均值和方差,且μ1≤μ2、σ1≤σ2。

为了统一平纹和斜纹织物纹理模型,可以利用式(2)对织物纹理进行统一建模,平纹织物纹理模型(式(1))可以认为是式(2)的特殊形式,即式(2)中ω1=1,ω2=0且μ1=μ2,σ1=σ2。

3 特征提取与分类学习

3.1 疵点特征提取

进行织物疵点判别时,需要从织物纹理图像中提取表征疵点的纹理特征。根据疵点检测算法,可以采用灰度共生矩阵法[11]提取无疵点织物的纹理特征,疵点织物则采用异常像素分析法[12]提取纹理特征。

利用灰度共生矩阵法需要选取有代表性的纹理特征,本文选取对比度(CR)和逆差分距(IDM)作为代表纹理特征,对比度反映图像的清晰度,逆差分距反映图像纹理的同质性。式(3)反映织物图像纹理的对比度,通常正常织物的对比度是有序且均匀分布,而有疵点的织物像素点明暗变化无序,相应的纹理对比度也会发生改变。式(4)反映图像纹理的均匀度,当出现疵点时,纹理的均匀度将会受到破坏,因此特征值CR和IDM可以较好地反映织物的纹理特征,用于判别正常区域和疵点区域。

(3)

(4)

式中:N为灰度共生矩阵的总行数(或总列数);p(i,j)为共生矩阵经过规范化处理后的元素。

当织物中存在疵点时,织物图像中的像素点亮度便会出现异常。为了定量描述像素点亮度异常,采用异常像素分析法提取织物疵点特征,异常像素分析法的核心思想是提取异常行程特征,主要包括亮度异常行程(LER)和暗度异常行程(DER)。LER定义如下:

(5)

式中:Q为量化后的像素值;CL为LER的行程长度;Sl为行程长度大于l的异常亮度的集合;Cs为亮度异常行程的总长度;s(k)表示第k个元素的量化级别;设定行程长度阈值l时,通常选取在正常纹理中包含亮度异常行程长度的90%分位数。

除了亮度异常特征LER之外,另一个核心特征是DER,定义如下:

(6)

式中:CD为DER的行程长度;Dl行程长度大于l的异常暗度的集合;Cd表示暗度异常行程的总长度;d(k)表示第k个暗元素的量化级别;DL阈值设定为织物高斯分布的置信区间下限。

为了表征所选特征值的有效性,选取常见的织物疵点图像,图像样本大小为256像素×256像素,如图4所示。

图4 常见织物疵点类型Fig.4 Types of common fabric defects.(a)Broken weft; (b) Lack of warp; (c) Random weft; (d) Nep;(e) Loose warp; (f) Dirty weft (g) Broken; (h) Lack of weft

以缺经疵点为例,将图像样本划分为4个互不相交的子区域,其中子区域1代表疵点区域,子区域2、子区域3和子区域4代表正常区域,如图5所示。计算疵点的4类特征值,结果如表1所示。

表1 不同区域的4类特征值Tab.1 Four types of feature value for different areas

图5 标记有疵点区域的样本Fig.5 Samples of marked defect areas and its feature value

子区域1的特征值明显高于其他子区域的特征值,即疵点区域的特征值明显高于正常区域,说明本文所选的4类特征值可以较好的表征疵点特性,捕捉异常像素点的存在。由于将图像划分为16个区域,每个区域采用4类纹理特征值,因此可以采用64个特征组描述织物纹理特性。

3.2 分类学习

采用机器学习中的分类算法,可以得到判别疵点的分类器。选取织物样本图像中互不相交的每个子区域作为训练样本,经过迭代训练才能获得适合的分类器,在整个训练过程中,首先提取每个训练样本的特征值,然后利用式(7)对特征值进行归一化处理。

Vm=(Vm-α)(N1×β)

(7)

式中:Vm为归一化后的特征向量;N1为训练样本的总数;α与β为归一化处理中的偏移系数。

经过归一化处理后各个特征值的权重较为接近,每个特征值对整体属性的影响力差异较小,训练后的分类器才能较为准确的描述特征值。分类器经过训练后可以用于检测样本织物,判断织物中是否包含疵点,织物的分类检测过程如图6所示。待测织物图像经过划分后,提取4类特征值并进行归一化处理,而后输入训练后的分类器之中,分类器将分类结果输出,如果结果为1,则为正常织物纹理,反之则判定存在疵点。

4 对比实验

为了验证本文疵点判别算法的可靠性,分别选取正常纹理样本和疵点样本进行评估实验。所有样本图像采用CCD线阵相机捕获,图像样本大小为256像素×256像素,每个像素点包含256个灰度级别,每幅图像被分割成16个大小为64像素×64像素的子区域,图像数据样本从每个子区域中获取,样本的数据集信息如表2所示。

表2 3种织物数据集信息Tab.2 Three types fabric datasets information

利用分类器对表2中的无疵点样本数据集进行训练,分类器训练参数α设定为0.01,参数β设定为0.02,经过10次迭代处理后,分类器得到疵点判定结果。为了进一步验证本文所提算法的优势,选用小波重构算法[13]、GMRF模型[14]、BP神经网络[15]与本文算法进行对比实验,结果如图7所示。

图7 4种算法的检测结果对比Fig.7 Comparison of detection results of four algorithms

由图7可见,从疵点检出正确率来看,小波重构算法的平均准确率为88%,GMRF模型的平均准确率为81%,BP神经网络的平均准确率为91%,本文所提算法的平均准确率为97%,高于前3种算法,可以更好地用于检测织物疵点,同时也说明影响检测准确率的因素主要与分类算法选择和特征值提取有关。

除了检测精度之外,还需对疵点判别算法的实时性进行检测,CPU处理器的选择对疵点实时性检测至关重要,为了进行对比测试,选取DSP T1 320C40、Pentium Ⅲ 450 MHz、Matrox Odyssey XCL、P4 3.0 GHz 4种处理器,分别对应选用小波重构算法、GMRF模型法、BP神经网络法与本文所提算法进行疵点检测,检测结果如表3所示。

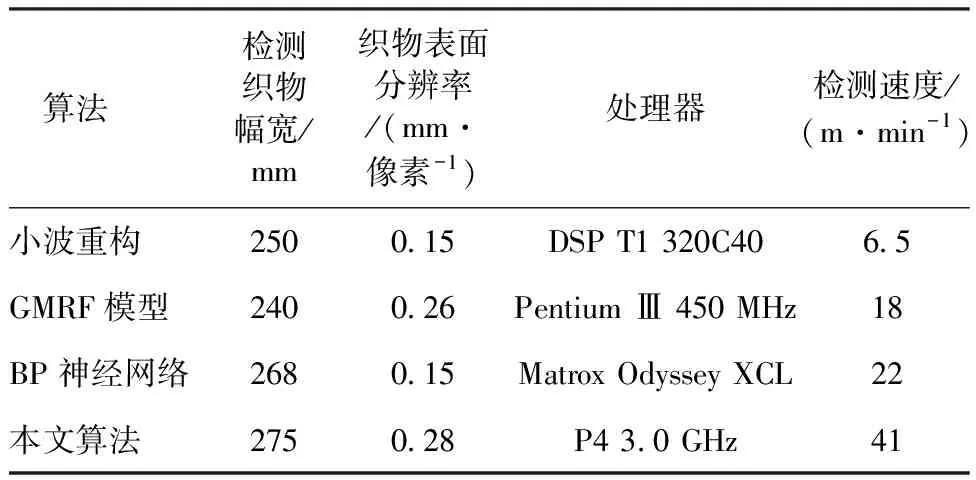
表3 4种织物疵点检测算法的检测速度Tab.3 Detection speed of four fabric defect detection algorithms

从表3可知,在织物幅宽接近的情况下,采用不同的处理器和检测算法,检测速度差异明显,采用本文的检测算法和处理器,检测速度可达41 m/min,表明本文检测算法在实时性方面具有较为明显的优势,也说明影响实时性检测效果的因素主要与织物幅宽、表面分辨率和处理器类型有关。

5 结 论

针对织物疵点算法中存在实时性不足问题,提出了一种基于机器学习的高实时性织物疵点检测算法,通过算法分析和对比性实验得出以下结论:

①采用高斯函数对织物纹理图像直方图进行建模,能够描述织物图像的灰度色调变化,选取对比度、逆差分距、亮度异常行程和暗度异常行程4类纹理特征刻画织物纹理并突出纹理中包含的疵点。疵点检测通过分类过程实现,仅对正常纹理织物进行训练后便可检测未知类型疵点。

②通过对比实验得出,本文所提算法的检出准确率高于其他传统检测算法,在织物幅宽相近的情况下,采用本文的检测算法和处理器,检测速度可达41 m/min,能够满足在线实时监测需求,可以应用于高实时性的工业检测环境之中。

今后的研究内容可以考虑如何减少原始图像256像素×256像素的量化级别,从而减少各个纹理特征的计算量,进一步提高检测算法的实时性。