一种大尺寸视觉测量系统标定方法

刘荣华，潘峰，刁奇，陈盟

（1.北京理工大学 自动化学院，北京 100081；2.中国船舶集团有限公司第七一六研究所，江苏，连云港 222061；3.哈尔滨工业大学 芜湖机器人产业技术研究院，安徽，芜湖 241000）

工业测量设备在进行自动化测量之前，通常需 要校准传感器的内部参数及标定传感器坐标系、测量设备坐标系之间的空间位姿关系，传感器内部参数校准属设备内参标定，传感器坐标系与测量设备坐标系位姿关系标定属设备外参标定，本文仅关注外参标定.外参标定，即以刚体位姿变换为单一目标的优化问题，在实际测量系统构建中广泛存在，如双目或多目立体视觉系统需要标定出任意两个二维相机之间的精确位姿关系[1]，自动驾驶汽车感知系统需要标定图像传感器、激光雷达等多个传感器与全局坐标系之间的关系[2]，应用于机器人自主规划与操作任务的视觉传感器，则需要标定出其到机器人基坐标系之间的关系（眼在手外）[3]或到机器人法兰坐标系之间的关系（眼在手上）[4].测量设备传感器的一个重要特点是工作范围越大测量误差也越大，对于大尺寸测量，为了获得足够的测量精度，不可避免地需要选择多个传感器进行拼接测量.对于工作空间不存在重叠的多个传感器，为了标定彼此之间的位姿关系，则需要引入中间测量设备或大尺寸标定靶标建立传感器之间的坐标联系.对于大尺寸测量系统，测量的基准特征可能不在高精度视觉系统的测量范围内，为了建立视觉传感器与测量基准之间的联系，同样需要借助中间测量设备进行标定，此时问题的关键转化为两个测量设备之间坐标系关系的求解.不同的外参标定方法依传感器的具体形式而不同，但一般地，均是建立以外参矩阵为优化目标的目标函数进行最小化求解.

对于双目或多目相机的外参标定，当两个相机视场存在大范围交叠时，经过内参标定的两个相机可同时采集公共视野图像，通过图像特征匹配求解相机外参矩阵，或者建立以内参外参为变量、以最小化重投影误差为目标的优化问题，同时标定相机内参和外参[5].当两个相机的视场不存在重叠或重叠较少时，一般通过已知结构参数的高精度靶标进行标定，如胡潇琨等[6]及胡茂邦等[7]借助两个空间位姿关系已知的固定平面靶标，通过两个相机分别单独采集平面靶标，建立平面靶标与相机之间的关系，进而求解相机之间的空间位姿关系.鲁亚楠等[8]及徐秋宇等[9]借助精密的二轴转台及固定不动的单个平面靶标实现无重叠视场相机外参标定，其首先根据单个相机在不同转台角度下的靶标图像标定靶标坐标系与转台坐标之间的关系，然后根据不同角度下每一个相机的每一幅图像标定出每一个相机与转台之间的坐标关系，最终将所有相机坐标系转换至同一个坐标系下描述.

相机与激光传感器的联合标定同样广泛应用于测量系统、机器人自主操作及自动驾驶等领域.康国华等[10]借助标定板实现相机与激光雷达之间关系的标定，其分别获取多组标定板点云中心点在相机坐标系和激光雷达坐标系下的坐标，利用迭代最近点算法精配准实现相机与激光雷达的联合标定.ZHOU等[11]借助直线建立相机与线激光传感器之间的约束关系，通过两步实现二者之间投影矩阵的求解：首先通过奇异值分解计算投影矩阵的线性解，最后通过Levenberg-Marquardt 优化线性解获取投影外参矩阵的最优解.YING 等[12]同样借助直线建立相机坐标系与线扫激光雷达坐标系直接的联系，但其通过解析法直接求解二者之间的投影矩阵.祝飞等[13]则利用V 型棋盘格，综合点-面、线-面和点-线约束优化和求解相机与线激光传感器的外参矩阵，具有更高的精度和稳定性.也存在两个三维传感器之间坐标关系的标定研究，如董方新等[14]为了实现双目立体视觉系统与三维激光系统之间位姿关系的标定，设计一种镂空棋盘格以便定位三维空间特征点，以外参矩阵的欧拉角参数和平移参数为变量，将特征点误差作为最小化目标进行优化求解.石照耀等[15]设计一种特征标准件结合仪器运动解耦线激光传感器与仪器之间的位姿关系，先求姿态参数欧拉角，再计算平移分量.王向周等[16]利用线扫描相机的高分辨率特性，采用平面二维棋盘格进行标定，首先推导线阵相机的图像坐标系和世界坐标系转化关系，再矫正标定棋盘格的图像畸变，在求解标定参数时，引入改进的遗传优化算法求解过程，提高成像系统的标定精度.马少鹏等[17]在研究室外竞技状态下运动员姿态摄像测量时，通过在运动员关节处粘贴标志点的方式获得关节点二维图像坐标、标定的相机参数进而获得关节点的三维坐标，计算各肢体的真实长度.常亮等[18]在进行相机和雷达联合标定时，首先建立雷达与图像的转换关系，实现目标从雷达坐标系到像素坐标系的转换，然后构建雷达特征图.

如图1 所示的大尺寸圆柱体工件，需要精确测量左侧插槽中分线在右端基准坐标平面内的投影角度.圆柱体工件右端基准坐标系B由自身圆柱轴线和上下两段沿径向贯穿的小圆柱轴线构建，圆柱体左侧插槽中分线由一套三维视觉测量系统通过扫描插槽点云测量.

图1 大尺寸圆柱体工件及视觉测量系统Fig.1 Large size cylinder workpiece and vision measurement system

为了实现测量目标，首先需要标定三维视觉测量系统坐标系S相对于基准坐标系B的空间位姿关系，然后将三维视觉测量系统测量的中分线坐标转换至基坐标系B下即可快速计算目标投影角度.

针对以上问题，提出一种大尺寸视觉测量系统标定方法，首先通过激光跟踪仪和三维视觉传感器采集固定不动的球体拟合球心数据，根据球心点集进行对齐实现三维视觉传感器坐标系S到激光跟踪仪坐标系L之间的关系标定，其次通过激光跟踪仪多次测量基坐标系B计算刚体变换矩阵的算术平均，建立激光跟踪仪坐标系L与基坐标系B之间的联系，最终获得三维视觉传感器坐标系S与测量基坐标系B之间的关系.

1 基于最小二乘标定方法的数学分析

1.1 基于最小二乘的点集配准

首先通过点集配准获得激光跟踪仪与三维视觉传感器之间的联系[19].假设三维视觉传感器的工作空间大部分处于激光跟踪仪的工作空间内，通过一个球面度较高的标准球放置在视觉传感器工作空间的n个不同位置，利用视觉传感器测得球心点集P={p1,p2,...,pn} ，利用激光跟踪仪测得球心点集Q={q1,q2,...,qn} ， 显然点集P和 点集Q之间的点对点对应关系已知，且存在如下变换关系

式 中：pi，qi，t，vi都 为 三 维 向量；R为 旋转 矩 阵；t为平移向量；R和t表征激光跟踪仪和视觉传感器之间的位姿关系；vi为对应球心误差，包含设备误差和拟合误差.

假设球心误差服从高斯分布，位姿关系的最小二乘解为

式中：wi为点对 (pi,qi) 的权重，且有wi＞0.式（2）中若令

则f(R,t) 为关于R,t的实值二次函数，通过坐标变换可将该二次函数转换为标准二次型，又f(R,t)≥0则该二次型至少是半正定的，因此该实值二次函数存在极值，且极值在偏导数等于0 处取得，也即

为此，固定旋转矩阵R，获得误差权重平方和关于平移向量t的函数为

式(5)对t求导，有

将式(8)代入目标函数(5)，得

令xi=pi-,yi=qi-，其 中xi，yi均 为 三 维 向 量，则得

因此，原优化问题等价于

故上述目标函数变为

优化问题(11)等价于

对式(13)，再令

则有

也即

式中令A=XWYT，对矩阵A进行奇异值分解，得

再令

则矩阵B为正交矩阵，矩阵C为正定矩阵，又对任意的正交矩阵R，正定矩阵C满足

也即

式(20)对任意正交矩阵R都成立，说明当B等于正交矩阵VUT时，可使BUΣVT的迹最大化，也即

上式中，如果正交矩阵R的行列式为1，则R为旋转矩阵，如果R的行列式为-1，则R为镜像矩阵.

考虑在无噪声的情况下，对于非共面点集P，矩阵A的奇异值均为正数，此时正交矩阵R必为旋转矩阵；对于共面但不共线点集P，矩阵A的最小奇异值为0，此时存在唯一一个旋转变换和一个镜像变换满足配准平方误差和为0；对于共线但不重合点集P，矩阵A的奇异值有两个为0，则存在无数个旋转变换和镜像变换满足配准平方误差和为0.

当点集P共面但不共线时，对矩阵A进行奇异值分解，有

且奇异值 σ1＞σ2＞σ3=0，

由于 σ3=0 ，单位向量u3和v3的方向不会改变A，也即存在两个正交矩阵

均能满足配准平方误差和为0，其中R1和R2一个为旋转矩阵，另一个为镜像矩阵.

考虑在有噪声的情况下，点集P共面或点集Q共面时，此时矩阵A的最小奇异值接近0；当矩阵A的所有奇异值均大于0，而正交矩阵R的行列式为-1 时，则是由于噪声过大，使该方法失效.

根据以上分析，显然当球心均匀立体分布在三维视觉传感器工作空间内时，标定结果具有更高的精度和可靠性.

1.2 基于最小二乘的旋转矩阵算术投影平均

为了建立激光跟踪仪与基坐标系之间的联系，通过多次测量基准特征建立基坐标系，获得多组基坐标系变换矩阵取平均以避免单次测量可能引入的随机误差.考虑基坐标系相对于激光跟踪仪的位姿矩阵表示为

其中对于三维欧氏空间，n次测量位置分量的算术平均为

类比欧式空间的算术平均，将下式最优解作为姿态分量的算术平均

式(27)中下标F表示矩阵的Frobenius 范数.通过式(26)和式(27)基于最小二乘分别计算位置向量的平均和姿态矩阵的平均，其中，姿态平均通过投影算术平均进行计算[20].

在S O(3)空间，定义旋转矩阵的算术平均为

根据式(21)可知，

式中

为通常意义上三阶实矩阵空间上的算术平均，由于旋转矩阵列向量相互正交，多次测量同一个姿态情况下，其姿态矩阵算术平均后的列向量仍然线性无关，故R¯的奇异值均大于0.式(29)和式(30)表明，基于Frobenius 矩阵范数的旋转矩阵平均，实为旋转矩阵关于欧氏空间上的算术平均在空间SO(3)上的投影.

1.3 空间坐标变换关系计算

假设激光跟踪仪坐标系L与基坐标系B的关系矩阵为，假设激光跟踪仪坐标系L与视觉传感器坐标系S与的关系为，假设视觉传感器坐标系S与基坐标系B的关系为，则可得到空间坐标变换关系

2 实验验证

2.1 仿真实验验证

通过仿真实验验证最小二乘点集配准方法求解坐标系关系的有效性.针对最小二乘点集配准方法，设计三组仿真实验验证点集大小、传感器精度和传感器位姿关系对标定结果的影响.为了评估配准精度，除了衡量用于配准点集的配准误差外，另通过传感器工作空间固定栅格点进行验证.实验设定两个三维传感器A 和B 工作空间大小均为40 mm×40 mm×40 mm，工作距离均为60 mm，验证精度的栅格点间隔10 mm，传感器候选精度设定为0.04，0.06，0.08 mm，随机生成三个传感器位姿关系设计值

仿真实验1，设定配准点集大小分别为10，20，30，传感器精度为0.06 mm，传感器位姿关系为T2，如图2 所示为对齐点集后的配准误差，图3 为栅格点验证误差，对应不同点集大小其误差均值分别为0.026 9，0.009 8，0.008 2 mm，误差标准偏差分别为0.011 5，0.004 3，0.002 5 mm.

图2 仿真实验1 配准误差Fig.2 Registration error in simulation test 1

图3 仿真实验1 验证误差Fig.3 Validated error in simulation test 1

仿真实验2，设定配准点集大小10，传感器精度分别为0.04、0.06、0.08 mm，传感器位姿关系为T2，如图4 所示为点集对齐后的配准误差，图5 所示为栅格点验证误差，对应不同传感器精度其误差均值分别为0.008 2，0.015 8、0.027 7 mm，误差标准偏差分别为0.002 5，0.004 9，0.010 1 mm.

图4 仿真实验2 配准误差Fig.4 Registration error in simulation test 2

图5 仿真实验2 验证误差Fig.5 Validated error in simulation test 2

仿真实验3，配准点集大小10，传感器精度为0.06 mm，传感器位姿关系分别为T1、T2、T3，如图6所示为配准误差，图7 所示为栅格点验证误差，对应不同传感器位姿其误差均值分别为0.005 8，0.008 2，0.007 3 mm.

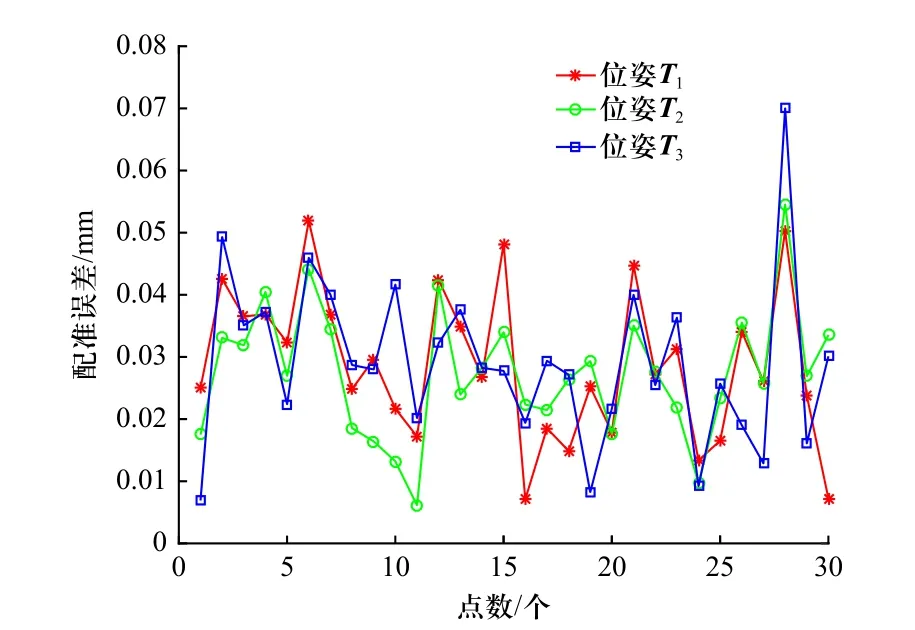
图6 仿真实验3 配准误差Fig.6 Registration error in simulation test 3

图7 仿真实验3 验证误差Fig.7 Validated error in simulation test 3

根据仿真实验1 可知，用于配准的点集数量越大配准精度越高，但点集增大到一定程度后，配准精度不再显著提升.因此，在实际标定中，可综合考虑数据采集效率和标定精度确定采集数据的数量.根据仿真实验2 可知，传感器自身的测量精度越高，配准后在验证点集上测试的误差越小，对应地说明配准精度越高.根据仿真实验3 可知，最终的配准精度也取决于两个传感器自身的位姿关系，这可以用来指导实际传感器的空间安装位置，使传感器自身位姿关系对标定精度影响较小.

2.2 真实实验验证

针对图1 所示的大型圆柱体工件（实验选用标准工件，长度5 923.5 mm，测量目标角度值为55.23°），搭建大尺寸视觉测量系统，测量系统包括三部分构成：一套传感控制系统精确定位右侧基准小圆柱轴线方向，一套机械定心机构精密限位大圆柱轴线方向，以及一套三维视觉传感器（由KEYENCE LJ-V7080激光轮廓仪和IAI RCS-SA4R 滑台组成，综合精度0.05 mm）精确扫描左侧插槽及测量左侧插槽中分线.

通过激光跟踪仪Leica AT960（精度0.025 mm+0.006 mm/m）建立基准坐标系与三维视觉传感器之间的关系，其中激光跟踪仪坐标系与基准坐标系之间通过多次测量直接求算术平均获得二者之间的位姿关系，激光跟踪仪与三维视觉传感器通过点集配准方法进行关系的标定.

通过传感控制系统及机械定心机构重复定位工件基准6 次，通过激光跟踪仪测量工件基准得

按第1.2 节，计算平均位姿得

将一个标准陶瓷球（标称直径20.003 8 mm，球面度0.001 mm）放置在三维视觉传感器工作空间不同位置，采集球面点云数据并拟合球心，同时保持标准陶瓷球固定不动，通过激光跟踪仪测量球心.如图8所示，通过三维视觉传感器采集陶瓷球点云，手动剔除非球面点云及边缘噪声较大区域点云，最后通过高斯滤波减少整体噪声获得目标点云，对于通过三维视觉传感器获得的陶瓷球表面点，统一采用基于正交距离的最小平方拟合算法拟合球心[21].

图8 三维视觉传感器采集的陶瓷球点云数据Fig.8 Ceramic ball dot-cloud collected by 3D vision sensor

考虑到实际测量时视觉传感器的测量误差是复杂的，且激光跟踪仪为接触式测量，为降低随机误差影响，将标准陶瓷球放置在20 个不同位置，且尽可能均匀分布于传感器工作空间内，测量球心点集如表1 所示.

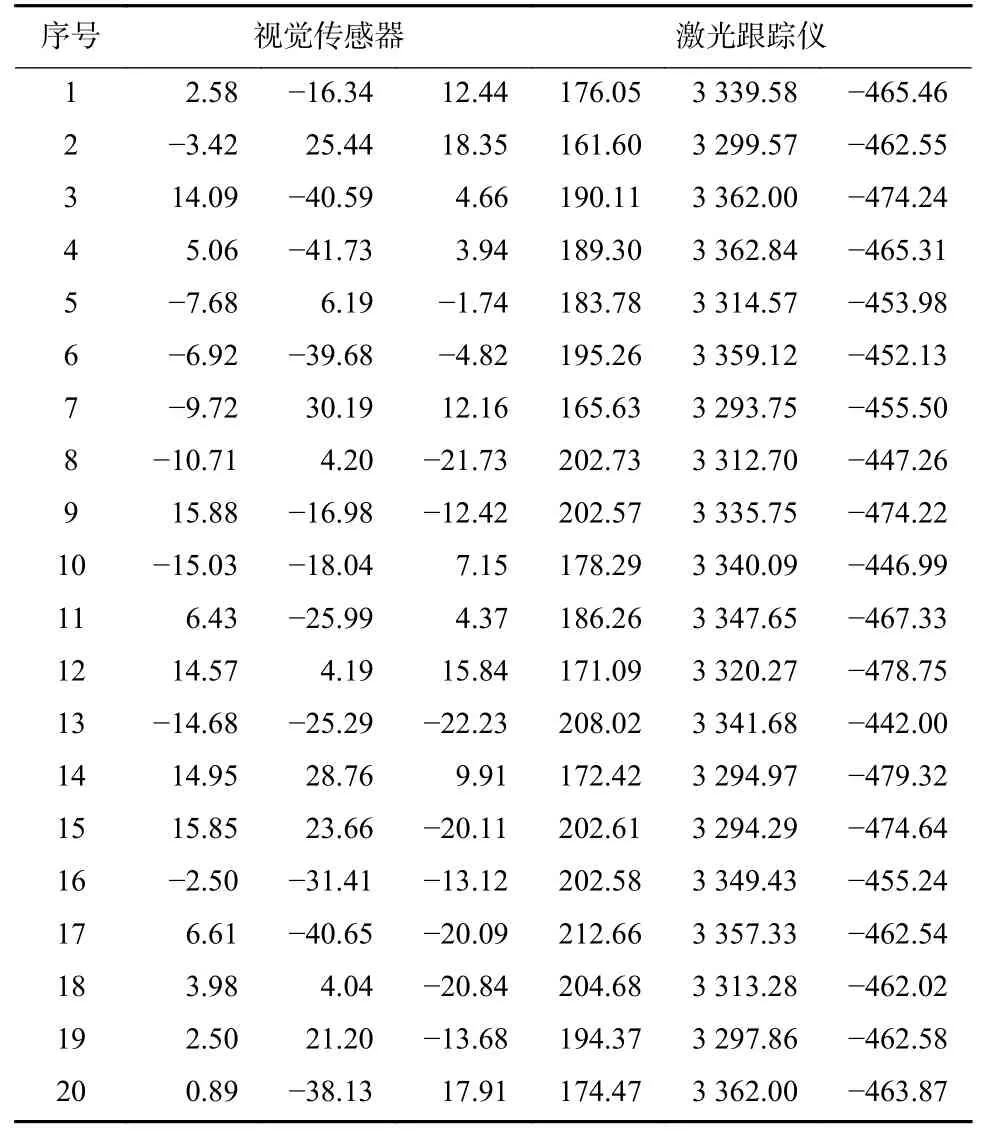
表1 拟合球心数据Tab.1 Imitated ball center data

根据以上测量点集，进行最小二乘配准，配准误差均值为0.093 mm，标准偏差为0.040 mm，配准转换矩阵为

考虑到激光跟踪仪与三维视觉传感器的实际距离，以上配准误差矩阵是合理的.

通过以上计算结果，得到基准坐标系与三维视觉传感器之间的位姿关系为

根据以上标定结果，反复测量该标准圆柱体工件的测量角度，连续测量10 次，测量结果如表2 所示，尽管测量存在固定偏差，但是测量值接近标准值，通过补偿可使测量系统角度测量达到较高测量精度.

表2 10 次角度测量值Tab.2 Measurement values for 10 angles

3 结 论

本文提出了一种基于最小二乘的视觉测量系统标定方法，该方法通过最小化点集配准误差解析计算两个坐标系之间的坐标转换关系，考虑到直接测量特征建立坐标系存在随机误差，基于最小二乘计算刚体变换矩阵的算术平均以减小误差.通过仿真实验分析了点集大小、传感器精度以及传感器坐标关系对配准精度的影响，仿真结果表明，点集大小对配准结果影响较小，传感器自身的测量精度越高，配准精度越高，同时也注意到传感器自身位姿也影响配准精度，且这种影响关系复杂，有待后续进一步研究.最后通过真实试验验证该方法的有效性.