土体压密注浆过程的抬升数值模拟

游庆如 李凤玲 彭春雷

（1.长沙理工大学汽车与机械工程学院，湖南 长沙 410114；2.湖南宏禹工程集团有限公司，湖南 长沙 410000）

0 引言

由于注浆的有效性和经济性，在交通、电站、隧道等基础加固领域得到了广泛使用。按浆液的作用方式分类，注浆可分为填充注浆、渗透注浆、压密注浆和劈裂注浆。李梦天等［1］团队研究表明：压密注浆较其他注浆方式更易引起地表抬动。在压密注浆过程中，抬动位移是影响注浆工程质量和安全的双刃剑，如Graf［2］最早提出了可以利用压密注浆抬升土体来纠正建筑物的倾斜，但抬升过大又会对原有建筑造成极大的安全问题，例如合肥地铁项目注浆时引起顶板隆起，最大达8.8 cm，造成了巨大的经济损失。因此，压密注浆的抬动建模和数值分析引起了广泛关注，许多学者针对压密注浆的抬动位移开展了理论计算、试验研究和数值模拟，取得了一定的研究成果。

在理论计算方面，唐智伟等［3］解释了注浆抬升的机制，采用镜像原理推导了压密注浆引起的地层抬升的解析解。李立新等［4］从随机介质理论出发，把浆泡看作是由无数微小单位构成的，浆泡的膨胀对土体的挤压可以看作微小单位对土体作用的总体叠加，土体抬升相当于注浆前后导致的地表抬动的高度差。陈娟等［5］利用最小势能原理，建立了有混凝土覆盖层注浆时的抬动变形理论计算模型。章敏等［6］根据随机介质理论和线性叠加原理，推导出了多浆泡在均匀及非均匀两种扩张模式下地表抬升变形的理论计算模型及其简化解。

在试验研究方面，Soga 等［7］开发了用于研究注浆抬动的试验系统，这个系统重点研究了注浆引起土体抬升的长效因素。冯旭海［8］使用振冲注浆工法开展室外试验，得到了注浆既加固了土体又造成了土体抬动。李梦天等［1］使用球形气囊模拟浆泡膨胀压密土体来研究土体抬动。

在数值模拟方面，Kummerer等［9］使用有限元法来描述压密注浆的工作效果。唐智伟等［10］使用有限差分程序FLAC3D在浆泡单元上施加膨胀压力模拟注浆抬升，为类似工程的设计提供了预测抬升效果的方法。Zhang等［11］也使用有限差分程序FLAC3D研究压密注浆对地表及上部结构的隆升作用，将地层膨胀引起的地表隆升视为一个随机过程，应用随机介质理论确定了均匀和不均匀作用下地表隆起变形，基于径向膨胀假设推导出相应的计算公式和简化方法，并将理论解、理论简化解和数值模拟解进行比较，验证模型的正确性。侯艳娟等［12］在使用非线性有限元软件ABAQUS 分析建筑物沉降恢复的基础上，研究了注浆抬升机制。李梦天等［1］使用离散元软件PFC2D 模拟压密注浆和劈裂注浆压密土体的过程，并将模拟结果与理论结果、试验结果进行对比分析。

前人有许多注浆抬动方面的研究，如使用膨胀单元来模拟浆泡扩张、扩张模式分为均匀扩张和非均匀扩张等，但是针对两种模式的适用情况的研究并不完善。本文基于数值模拟手段，使用有限元软件COMSOL 建立了土体压密注浆两种浆泡扩张模式的数值模型，通过数值解与前人的研究进行对比，验证数值模型的正确性。从数值模型方面对浆泡均匀扩张和非均匀扩张的适用情况进行研究，分析得到深层土层适用均匀扩张，浅层土适用非均匀扩张。在此基础上，还分析了注浆孔深度、注浆量、土体种类与注浆抬动位移的关系。通过分析模拟结果得到压密注浆的变形规律，为实际的注浆施工提供参考。

1 浆泡扩张引起地表抬升的理论解释

1.1 理论解释

压密注浆广泛应用于松软地层加固。因浆液浓稠、地层松软，注浆孔底部浆液会呈现球形浆泡，并随着浆液的注入而膨胀压密土壤。小孔扩张理论常常应用于压密注浆的土壤浆液力学分析方面，由小孔扩张理论可知，压密注浆模型可分为浆泡、破坏区域、塑性区域和弹性区域［4］，其中塑性区域、破坏区域和浆泡扩展机制复杂，注浆抬升地层的核心问题是挤压土体引起的土体位移，土体中的应力变化是次要的［13］，土体的抬动位移取决于弹性区域的弹性形变，本项目只研究浆泡间接对弹性区域造成的弹性变形，而忽略注浆孔附近的浆泡、破坏区域、塑性区域及部分弹性区域，并将注浆抬动视为弹性土体中的球形扩张问题。本研究采用文献［10］中提出的两种浆泡扩张模式，分别为均匀扩张和非均匀扩张，压密注浆如图1所示。

图1 压密注浆示意

1.2 基本假设

由于土体的非均质性和浆液的时变性等特点，注浆的实际过程十分复杂。为了简化计算，本文做出以下假设：①假设岩土体是线弹性、均质、各向同性的，遵循小变形规律；②假设为极浓稠浆液，在土体中不发生渗透，土体变形在浆液的挤密作用下瞬间完成；③假设塑性区域扩张时并未扩张到膨胀球区域之外。

2 浆泡扩张引起地表抬升数值模拟

2.1 数值模拟

目前，使用数值模拟在压密注浆抬升效应方面的研究通常基于使用“给定应变”方法或“给定压力”方法来模拟注浆引起的土体膨胀。“给定应变”通过在注浆土壤中施加适当的应变值来模拟注浆的注入，“给定压力”是对注浆孔周围岩体施加指定压力来造成岩体产生变形。相对来说“给定压力”的方法更接近注浆的实际情况，如现有的研究中Nicolini 等［14］使用“给定压力”的方法，但是比“给定应变”的方法要复杂，不易建立注浆量与地表抬动的关系。在实际的工程注浆中常用注浆压力和注入量作为注浆结束标准。由于注浆量易于控制，且为了达到给定的膨胀球体积扩张，本研究采用“给定应变”的方法。

在使用有限元软件COMSOL 时，通过固体力学接口，对膨胀球边界施加两种指定位移来模拟膨胀球的均匀扩张和非均匀扩张。假设土壤模型为弹性材料，弹性模量为10 MPa，泊松比为0.3，膨胀球分别位于地下2 m、3 m、5 m、10 m、15 m 深度处，膨胀球初始半径为1.5 m，注浆使得体积膨胀率为10%。边界条件设置如图2所示。

图2 边界条件

求解时分两个研究步骤，均采取稳态求解，求解第一步先进行地应力平衡，第二步进行膨胀扩张，对于不同注浆量的模拟，使用辅助扫描的方式得到不同大小的扩张，根据体积守恒即得到不同的注浆量。求解后两种扩张地层抬动模式位移分布云图如图3所示。

图3 均匀扩张和非均匀扩张引起的地层抬升云图

2.2 数值模型正确性验证

COMSOL解与Zhang等［11］文献中的结果进行对比如图4 所示，结果表明均匀扩张随机介质法和均匀扩张简化法及均匀扩张COMSOL 解曲线变化趋势相同。各个点的地面抬动高度也彼此基本一致，从而验证了COMSOL数值解的有效性。

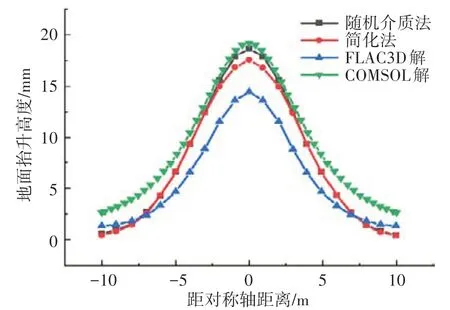
图4 COMSOL解与前人解对比

3 模拟结果与讨论

3.1 不同注浆孔深度的比较

不同深度的均匀扩张和非均匀扩张下的抬动高度如图5所示。可以看出地表抬动最高处位于注浆孔上方，随着注浆孔深度的增加，相同的注入量条件下，地表抬动位移变小，可见在地层深处注浆时不易发生抬动，地表浅处注浆时发生抬动较大。

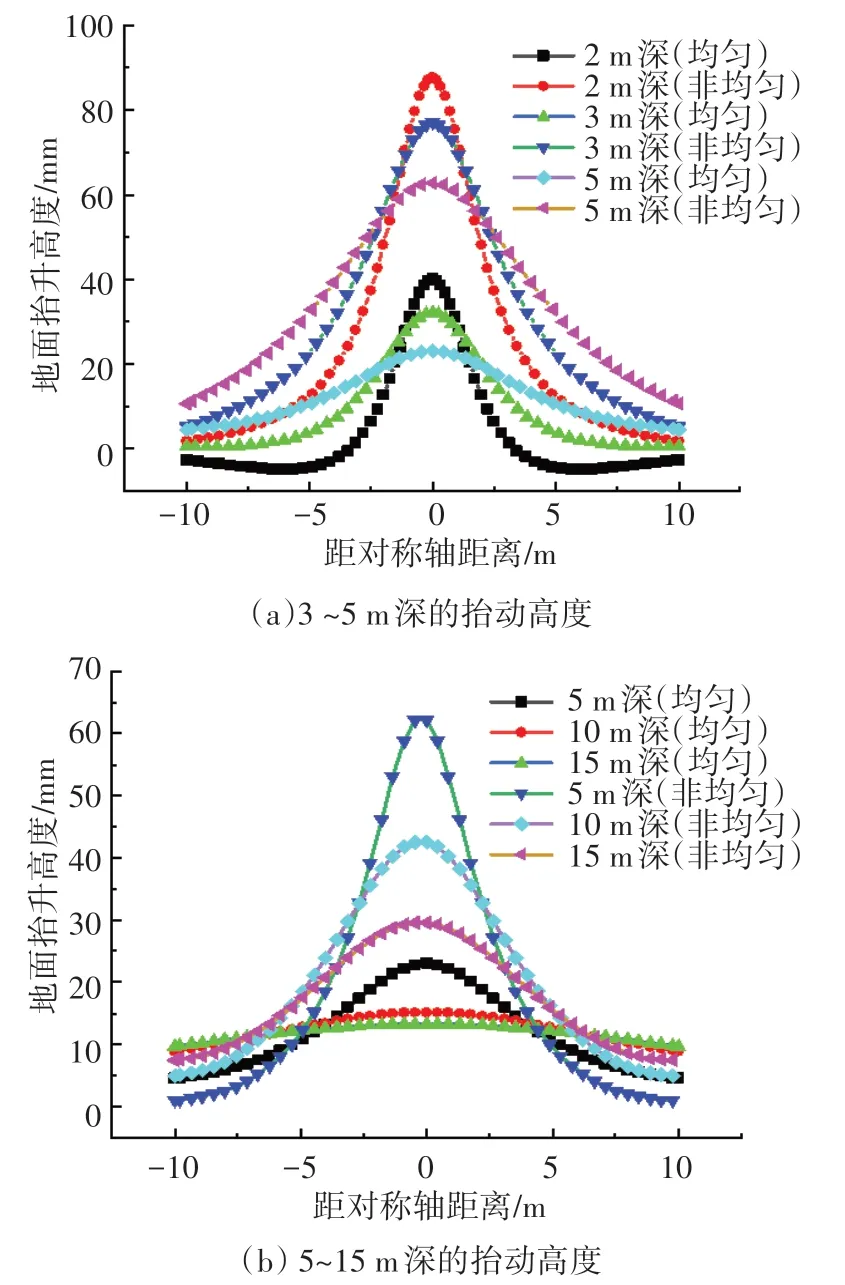
图5 不同深度下的抬动高度

3.2 均匀与非均匀扩张的比较

均匀扩张、非均匀扩张和理论模型在不同深度的最大抬升量的关系如图6 所示。可以看出，小于3 m 深的注浆抬动，非均匀扩张与理论模型下的结果相近，而在深于3 m 的地层均匀扩张模式下的值更加准确。出现这种情况的原因是在地层无限深处，地层各项受力均匀，属于理想的圆孔扩张，扩张形状呈现完美球形，而在较近地表层，注浆孔上方的受到的地层弹力小于注浆孔下方的区域，并非呈现一个球形，而是一个类偏椭球形状，此时非均匀扩张的解更加符合地层移动规律。

图6 数值解与理论解对比

3.3 不同注浆量之间的比较

根据体积守恒定律，膨胀球体积膨胀量等于注入的浆液量，通过不同的膨胀大小模拟出注浆量与抬动大小关系，分别给予体积膨胀率为6%、8%、10%、12%，得到不同注浆量下的抬动关系。不同注浆量下地层抬动大小如图7 所示。可以看出注浆量与地层抬动呈现线性增长的模式，但是处于不同地层的增长斜率并不是一致的，浅层区域增长率高，深层增长率低。

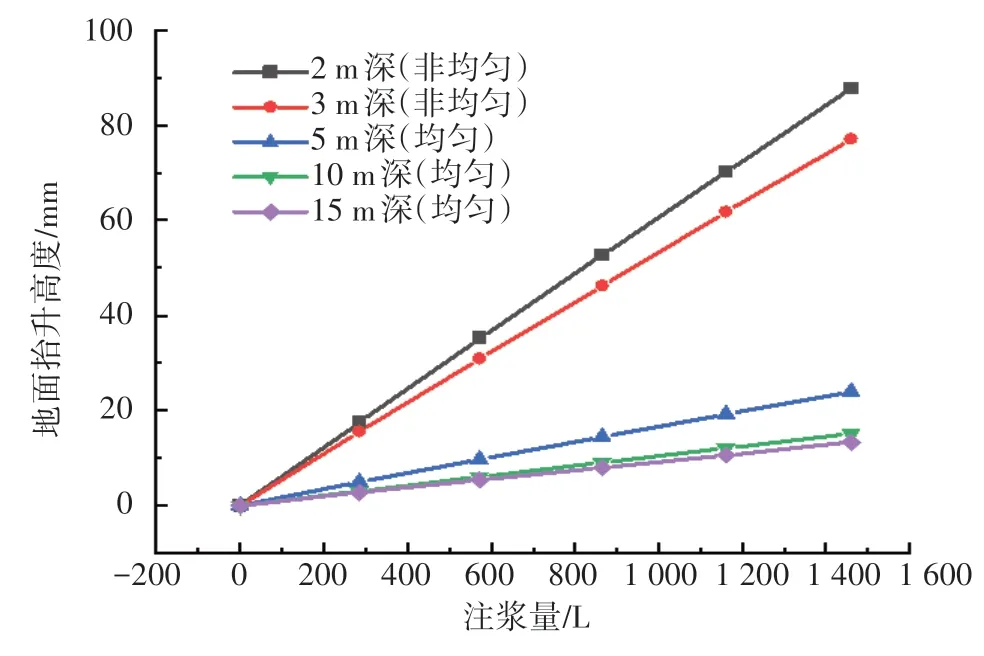
图7 不同注浆量下的抬动大小

3.4 不同土体的比较

不同的土体具有不同的性质，但是土的泊松比是很难精确得到的，常见土体的弹性模量和泊松比的近似值［15］见表1。

表1 常见土的弹性模量和泊松比

分别给予土体10 MPa、30 MPa、50 MPa、70 MPa、90 MPa的弹性模量，得到了不同弹性模量土体下的抬动关系。同一深度非均匀扩张模式下，不同弹性模量土体的抬升高度如图8 所示。不同弹性模量下的抬动太小几乎相同，也就是在注浆量相同的情况下土体抬动位移与土体弹性模量关系较小。

图8 不同类土体的弹性模量与压密注浆抬升位移量化结果

分别给予土体0.15、0.20、0.25、0.30、0.35、0.40泊松比，得到了不同泊松比土体下的抬动关系，同一深度非均匀扩张下不同泊松比的土体抬动大小如图9 所示。当泊松比为0.15 时，最大抬动为69.97 mm；当泊松比0.4 时，最大抬动为60.63 mm。抬动位移随着泊松比的增大而减小，相对于注浆孔深度的影响，土体泊松比对注浆抬动影响较小，但就抬动的范围而言，泊松比较大的土体抬动的范围更广。

图9 不同土体泊松比下的抬动大小

4 结论

①通过有限元分析软件COMSOL 建立了土体压密注浆地面抬动模型，将模型的仿真数据与前人研究成果进行对比，验证了模型的正确性。

②通过仿真模型分析，在同样的注浆量条件下，影响注浆抬动大小的主要因素为注浆孔深度。随着注浆孔的加深，地面抬动位移迅速变小；随着注浆孔的加深，浆泡形状扩张从非均匀渐变为均匀扩张，在地下3 m 以下区域应使用均匀扩张模型预测注浆抬升，在较浅区域应使用非均匀扩张模型预测注浆抬升；由体积守恒定律，得到了注浆量与抬动大小的关系，抬动位移与注浆量成正比，而抬动位移的变化率与注浆深度成反比；比较不同土质对土体抬动的影响，在相同的注浆量下土体的弹性模量对抬动高度影响较小，抬动位移随着土体泊松比的增大而减小，抬动的范围随泊松比的增加而增大。为了计算简单，本模型将土体考虑成线弹性体，但现实情况是土体力学性质复杂，且具有不均匀性，在后续的研究中还需进一步分析。