板状构件粘结强度的非线性超声导波检测

江梦慧，徐吉超，朱武军，项延训

(华东理工大学，上海 200237)

0 引 言

粘结是利用粘结剂在连接界面上产生的机械结合力、物理吸附力和化学键合力使两个粘结件连接起来的工艺方法，不仅适用于同种材料，也适用于不同材料间的连接。粘结结构广泛应用于航空航天、国防军工、车辆船舶等各个领域[1-3]，如固体火箭发动机燃烧室包覆层、飞机机体金属粘结[4-5]。粘结强度很大程度上决定着粘结构件的力学性能，是评价粘结构件是否合格的重要指标，因此国内外学者对粘结构件的粘结质量检测进行了大量研究。

超声无损检测技术具有检测灵敏度高、便捷高效等优点，广泛应用于工程实践中。超声导波可以进行长距离、大范围检测，提高检测效率和精度，更适用于板状结构的检测。在板状粘结构件的超声检测中，传统的超声导波检测技术可以表征粘结构件中的孔洞、裂纹、脱粘等缺陷[6-7]，但无法检测粘结构件的粘结强度、微小损伤以及早期性能退化情况。非线性超声导波检测技术可以弥补传统线性超声检测的缺点。材料性能的退化伴随着材料微观结构的改变和非线性力学行为，从而产生超声导波传播的非线性。因此，可以提取超声检测信号中的非线性特征信号，实现板状构件粘结强度、微小损伤以及早期性能退化等的检测和评价。Younghouse[8]推导并分析了粘结层刚度系数对基波和二次谐波幅度的影响。文献[9-10]对在多层结构中超声导波二次谐波产生问题进行了理论分析，建立了非线性弹簧模型，利用应力波因子来定征粘结结构界面粘结强度，结果表明应力波因子随着固化时间的增长而增大。Shui等[11-12]对粘结试件进行高低温循环疲劳和冲击载荷的非线性超声检测实验，发现在一定范围内超声非线性参数随着高低温循环疲劳和冲击载荷次数增加而增加。Li等[13]采用数值模拟方法，证明了超声非线性参量随着粘结层微裂纹密度增大呈线性增长趋势。国内外学者通过实验研究，建立了超声非线性参量与固化时间、应力循环次数、微裂纹密度等之间的关系，但尚未明确超声导波非线性参量与粘结强度之间的关系。

鉴于板状构件粘结强度早期检测的重要性，且对检测精度要求较高，本文针对不同粘结强度的粘结构件进行非线性超声导波检测。基于不同固化工艺构造了不同粘结强度的铝合金-环氧树脂-铝合金板粘结构件，使用非线性超声导波检测技术对板状粘结构件进行检测，测量并计算超声非线性参量，并通过拉伸实验测量粘结强度，建立超声非线性参量和粘结强度之间的关系。

1 粘结结构中的非线性超声导波

在粘结构件中，将上下粘结基体和中间粘结层简化为三层结构，示意图如图1所示。根据导波部分波分析方法[14]，在三层固体板中某个确定的导波由12 个满足边界条件的部分波组合而成。在粘结层与被粘接层界面处，应满足位移连续、法向和切向应力连续，可描述为

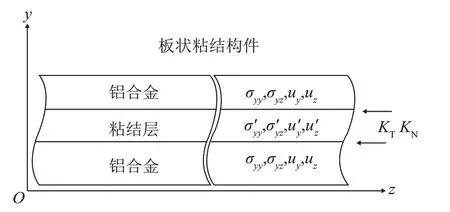
图1 实验板状构件示意图Fig.1 Schematic diagram of experimental plate bonded component

式中：σyy，σyz分别是法向和切向应力；KN，KT是粘结界面的法向和切向界面刚度系数；uy，uz是质点沿y轴和z轴位移。由边界条件和波动方程，粘结结构中超声导波的频散关系可以描述为[15-16]

式中：ρi、λi、μi分别是每层固体板的密度和二阶弹性常数；M是边界条件方程的系数矩阵。一般可以计算数值解，得到频散曲线。

假设材料是无频散、无损耗的均匀介质，在每一层固体板中，由两个横波和两个纵波组成，分别用T和L表示横波和纵波，但仅基频纵波位移分量自作用产生的驱动二次谐波才具有积累效应[17]，第i层中具有积累性质的驱动二次谐波幅值可以表示为[18]

式中：A(i)，B(i)，C(i)是每层材料的三阶弹性常数。结合界面声非线性反射和导波模式展开分析方法，得到完备的超声导波二次谐波声场解析解，并将超声导波非线性参量定义为[18]

式中：A1，A2分别为基频和二次谐波幅值。由式(4)可知，超声导波非线性参量与三阶弹性常数之间存在着定量关系。

粘结构件的粘结强度取决于金属被粘结层与粘结层之间的界面强度和粘结层的自身强度。界面粘结力的主要来源是分子间氢键，根据氢键和弹簧模型，可以将单位面积上的法向界面粘结力Fn表示为[19]

式中：h是环氧树脂平面和金属平面之间的距离；ron是氢键长度在法向上的投影；D(ron)为粘结界面上的弹簧长度分布函数。单位面积上氢键数量越多，粘结界面上的结合能高，宏观表现出的超声非线性较微弱；反之，单位面积上氢键数量越少，粘结界面上的结合能低，宏观表现出的超声非线性较强烈[20]。

在外界载荷下，环氧树脂粘结剂内部发生较大形变，用非线弹性本构模型来描述其非线性行为[21]，其内部产生的应力σ与内部环氧基团和固化剂之间形成的交联长度、密度、机械连接等有关。

因此，在有限振幅超声激励作用下，粘结结构的应力由粘结界面的法向结合力和粘结层内部的应力构成，表达式为[20]

一般情况下，粘结强度的下降，主要表现为介质的三阶弹性常数的增加。在有限幅度超声导波信号激励下，可近似认为粘结结构产生的应力只与介质的三阶弹性常数有关，可表示为

结合式(4)和式(7)，粘结结构的粘结强度的变化会引起三阶弹性常数的改变，其非线性超声参量也会发生相应的变化，可以得出：

由式(8)可知，超声导波非线性参量与粘结强度存在着某种对应关系。这为粘结强度的非线性超声导波检测提供了理论支持。

2 实验系统及试样制备

2.1 实验系统

本实验基于Ritec RAM-5000 SNAP非线性高能超声测试系统建立的实验平台如图2 所示。利用RAM-5000 SNAP 系统产生的高能量脉冲信号经过可调步进衰减器后加载到压电超声换能器上，压电超声换能器将电信号转换为超声振动，通过耦合剂入射到粘结试样中，有限幅度的超声信号与界面微观结构相互作用，传播过程中由于介质的非线性应力-应变关系产生畸变，最后被压电超声换能器接收，经过后续的功率放大器放大处理后输入到RAM-5000-SNAP系统和示波器中，对数据进行显示和保存。二次谐波信号通常比较微弱，为了接收到较明显的二次谐波信号，实验中选择用中心频率为f的窄带压电超声换能器来激发信号，选择中心频率为2f的宽带压电超声换能器来接收信号。

2.2 粘结试样制备

本文实验中的金属粘结试样使用Al7075-T6铝合金材料，尺寸为300 mm×50 mm×2 mm；选用环氧树脂双组份液态工业胶黏剂，粘结层厚度约为0.2 mm。第一组试样是5个不同固化温度的粘结试样，固化剂和环氧树脂质量比均为5∶5。降低固化温度需要延长固化时间以达到相同的固化完成度，固化工艺如表1所示。第二组试样是5个不同固化比例的试样，环氧树脂和固化剂的比例分别为3∶7、4∶6、5∶5、6∶4、7∶3，在常温25℃下固化24 h，固化工艺如表2所示。

表1 第一组金属粘结试样固化工艺Table 1 The first set of bonded metal samples

表2 第二组金属粘结试样固化工艺Table 2 The second set of bonded metal samples

3 实验与结果分析

3.1 超声导波二次谐波模式选择

超声导波具有多模式和频散基本特征，一般来说，其复杂传播特性导致二次谐波的发生效率非常低，不便于实际测量。积累增长二倍频导波产生需要满足特定条件。研究表明，当导波基频和二倍频满足相速度匹配、群速度匹配和非零能量流，就能够在固体板中激发出具有积累效应的二次谐波，即随着传播距离的增长，非线性超声参量呈增加趋势。文献[22-23]认为群速度匹配不是超声导波产生强烈非线性效应的必要条件，且在实际测量中难以满足群速度严格匹配这一条件。

使用Disperse 软件绘制铝合金-环氧树脂-铝合金粘结构件中的频散曲线，相关参数如表3 所示。由图3(b)可得，在频厚积为3.97 MHz·mm，即中心频率为0.94 MHz 时，与理论上的相速度完全匹配。

表3 粘结构件材料参数Table 3 Material parameters of bonded samples

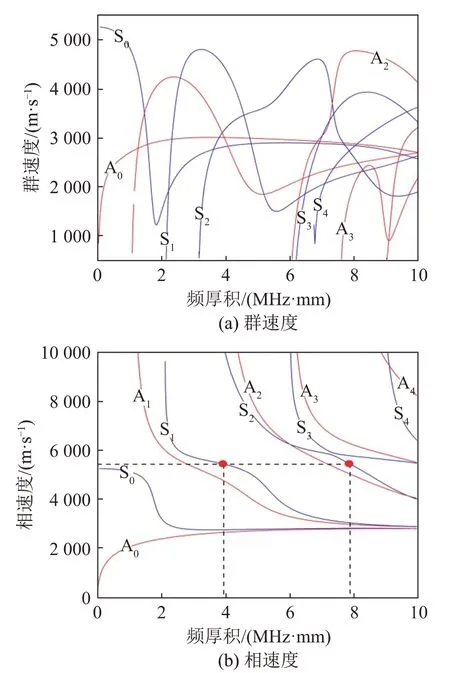
图3 金属粘结构件超声导波频散曲线Fig.3 Dispersion curves of ultrasonic guided waves in the bonded metal components

在中心频率为0.94 MHz 时，基频S1模式与二倍频S2模式的相速度相等，其相速度为5421 m·s-1，由Snell定律设置入射角为29.5°。在铝合金粘结试样上，保持激发换能器位置不变，移动接收换能器位置，使得收发换能器之间的间隔从60 mm增加到150 mm，其他设置和参数保持不变，间隔每增加10 mm进行多次测量，取其平均值作为最终测量结果。以传播距离为70 mm 为例，结果如图4(a)所示。对图4(a)中的第一个波包，即S1模式，进行快速傅里叶变换，结果如图4(b)所示，分别提取基频和二倍频幅值A1和A2，并通过公式计算归一化非线性超声参量A1/A22。

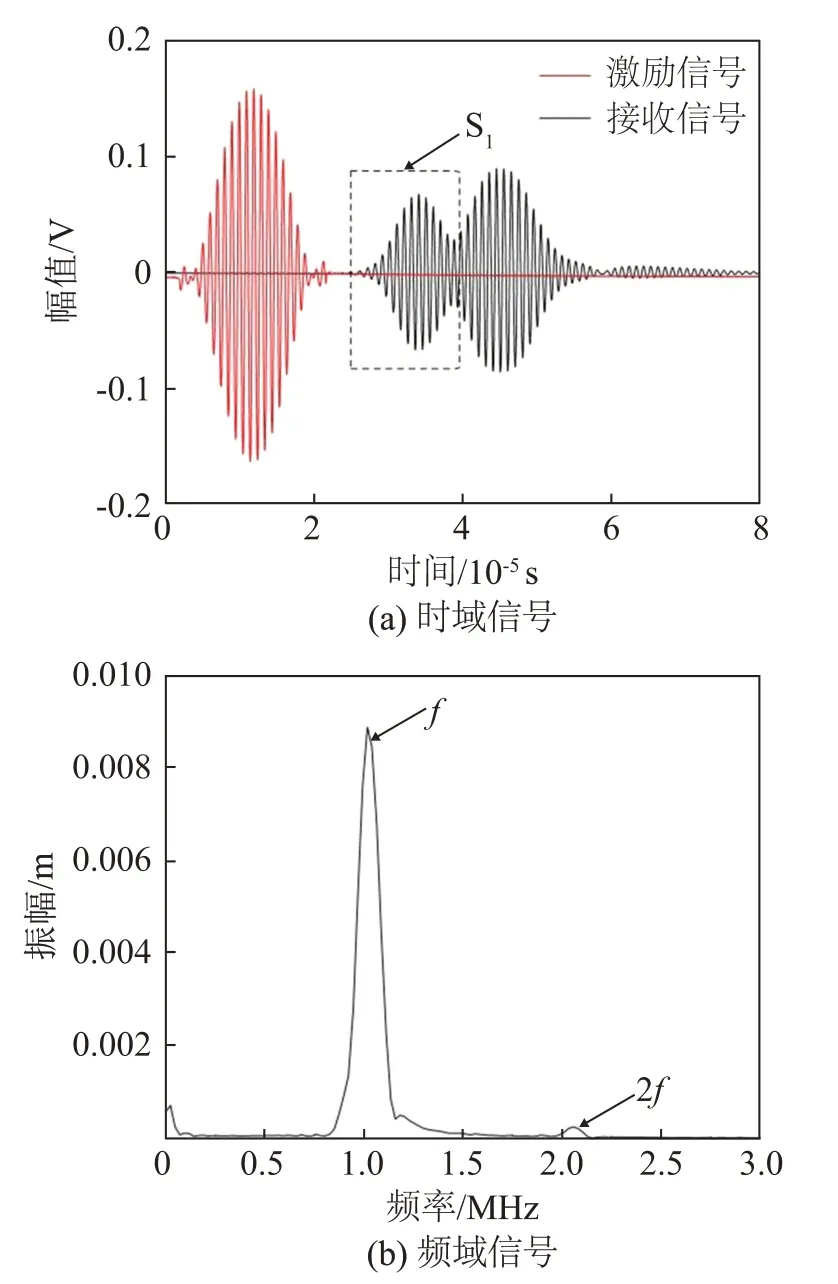
图4 传播距离70mm处的接收信号Fig.4 Received signals at the propagation distance of 70mm

在中心频率为0.94 MHz 附近，调整中心频率和入射角度，进行不同传播距离上超声信号的测量。实验结果表明，选择中心频率为1.02 MHz、20个周期、经汉宁窗调制的正弦脉冲信号作为激励信号，经角度为29.5°的斜劈换能器入射到板状粘结构件中，非线性超声参量具有良好的积累效应，结果如图5所示，红色直线为拟合结果。

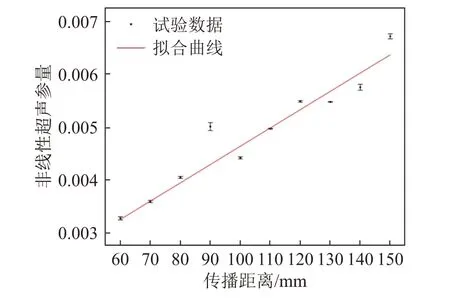
图5 非线性参量随传播距离变化趋势Fig.5 Variation of acoustic nonlinearity parameter with the propagation distance

3.2 粘结强度测试

在粘结构件固化完成后，通过超声检测系统进行非线性超声导波测量实验。使用RAM-5000-SNAP 系统激励出中心频率为1.02 MHz、20 个周期、经汉宁窗调制的正弦脉冲信号，经激发超声换能器和角度为29.5°的有机玻璃斜块，传播到待测粘结构件中，在距离激发超声换能器90 mm处放置接收超声换能器接收检测信号。实验测量示意图如图6所示。

图6 超声波检测的实验示意图Fig.6 Schematic diagram of the ultrasonic test experiment

在每根试样上进行同样的测量，选取2个不同的位置进行测量，每个位置点测量3次，取这6次测量的平均值作为最终结果。对所测的超声信号的第一个波包，即S1模式，进行快速傅里叶变换，分别提取基频和二次谐波频率下幅值的最大值，计算出非线性超声系数，得到每组粘结试样的非线性超声系数。

参考GB/T 6396—2008复合钢板力学及工艺性能试验方法[24]，用静压力通过相应的粘结试验装置使粘结试样结合面承受法向拉力，使其分离，以测定其粘结强度。从粘结试样上切割出50 mm×50 mm大小的样胚用于检测，将样胚放入万能试验机中，以1 mm·min-1的速率对样胚平稳施加载荷，直至分离，拉伸实验实物图如图7(a)所示，实验过程中的力与位移曲线如图7(b)所示。记录分离时的最大载荷，计算粘结强度R：

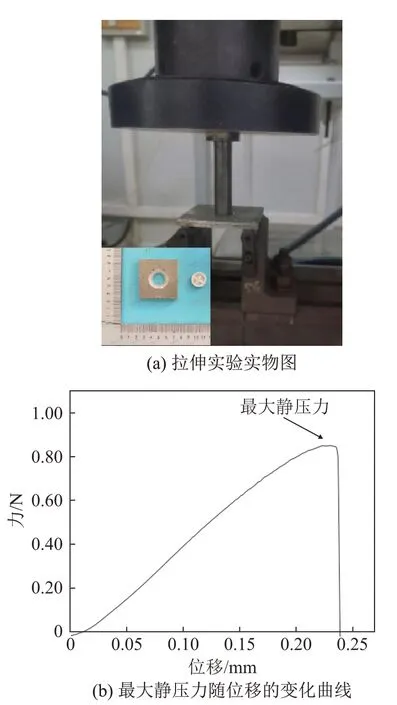
图7 金属粘结试样常温拉伸实验Fig.7 Tensile test of the bonded metal sample at room temperature

其中：F为最大静压力，S0为环形粘结面面积。

3.3 结果分析

非线性场声导波实验结果如图8所示。拉伸实验结果表明，随着固化温度的增加，粘结强度先增大后减小。在固化反应过程中，温度和时间是影响固化反应的重要因素。如果固化温度过低，分子链运动困难，交联的密度过低，固化完成度低，固化不完全进而造成粘结强度小。如果固化温度过高，容易引起粘结胶液流失或粘结胶层脆化，导致粘结强度下降。因此，随着固化温度的提高，交联密度不断增加，粘结强度也随之提高；达到最佳固化温度后，继续提高固化温度反而会造成粘结强度的降低。

图8 非线性超声导波检测的实验结果Fig.8 Experimental results of nonlinear ultrasonic guided wave tests

随着固化剂含量的增加，粘结强度先增大后减小，在固化比例为5∶5 时，粘结强度达到最大。随着固化剂含量的增加，环氧树脂与固化剂的交联反应越来越充分，其形成的网状聚合物密度增加，粘结强度不断增强。当固化剂含量继续增加时，与环氧树脂充分反应后多余的固化剂不利于环氧树脂扩散到粘结界面上，造成粘结强度的下降。

非线性超声导波测量结果表明，随着固化温度的增加，非线性超声系数先减小后增大。随着固化比例的增加，非线性超声系数先减小后增大。从两组实验结果可以看出，当固化工艺发生变化时，粘结强度与超声导波非线性参量有着相反的变化趋势，即板状构件粘结强度越大，其非线性参量越小。

4 结 论

针对板状构件的粘结强度检测，本文基于非线性超声导波检测方法，对板状构件的粘结强度进行了检测。首先选取并验证具有积累效应的非线性超声导波模式对，再利用基频波信号和二次谐波信号幅值计算非线性参量。实验结果表明，非线性参量与粘结强度有着对应关系，粘结强度越大，超声导波非线性参量越小，拉伸试验检测结果也验证了非线性超声导波实验的可靠性，为工业检测板状结构粘结强度提供了有效方法。