敷设空腔覆盖层水下复杂目标的声散射特性研究

李静，马晓川，李璇

(1.中国科学院声学研究所，北京 100190；2.中国科学院水下航行器信息技术重点实验室，北京 100190；3.中国科学院大学，北京 100049)

0 引 言

目标声散射特性研究是开展水下平台隐身设计和探测的基础支撑，有着广阔的发展前景和实用价值[1]。为了降低目标散射，提高结构隐身性能，水下平台表面往往敷设有吸声覆盖层。因此对敷设吸声覆盖层水下复杂目标的声散射进行预报和分析非常重要。

国内孙阳等[2]研究了吸声覆盖层的声学特性并对水下单层目标的隐身效果进行了预报。文献[3-5]中汤渭霖和范军等组建的研究团队对水下目标敷设覆盖层的声特性开展了十几年的研究，在理论研究、材料研究和试验研究这三个方面都取得了许多成果。

目前，水下目标声散射问题的研究方法主要有三类：理论解法、近似方法和数值解法。理论解法如瑞利(Rayleigh)简正级数解[6]、积分方程法[7]等，可以从原理上解释声散射问题，但是仅限于简单几何形状目标，比如球、圆柱等。近似方法如基尔霍夫(Kirchhoff)近似[8]、板块元方法[9]等，可适用于目标趋于复杂的情况，但是在频率偏低时无法获得准确结果。数值解法如边界元/有限元方法[10]等，适用范围非常广，可以解决大部分情况下的目标声散射问题，但是当应用于中高频的大型目标时，其对计算算力的要求非常高。

敷设吸声覆盖层的水下平台结构往往很大，所以对其进行中高频声散射研究选择利用板块元方法。板块元方法以Kirchhoff 近似为基础，通过把目标曲面近似为一组平面板块元，将所有面元的散射声场叠加近似得到复杂目标的总体散射声场，从而将面积分运算转化成代数运算并与目标表面声反射系数联系起来。此后刘成元等[11]将戈登(Gordon)积分引入板块元方法，解决了板块元方法在计算中可能出现的不稳定问题。针对潜艇等水下复杂目标的分析研究已经有很多，但是通常情况下目标表面有无均匀吸声覆盖层时的声散射特性预报的研究较多[12-14]，对敷设空腔覆盖层的水下复杂目标散射特性预报的研究较少。然而空腔覆盖层是改善声学性能的重要结构。文献[15-16]中的研究证明了空腔覆盖层可以有效提高结构的声学特性，但是由于该结构过于复杂，使得目前针对水下复杂目标敷设空腔覆盖层的声散射特性研究较少。

本文针对敷设空腔覆盖层的水下复杂目标开展声散射特性仿真研究。以BeTSSi Ⅱ潜艇模型[17]为例，通过对比敷设空腔覆盖层与未敷设覆盖层、敷设等厚均匀覆盖层时潜艇目标强度方位-频率谱的差异，讨论敷设空腔覆盖层对水下复杂目标的声散射特性的影响。在数值仿真计算的过程中，文中首先利用建模软件对潜艇外壳进行建模，然后利用分层近似法和传递矩阵方法得到敷设变截面空腔覆盖层模型的声反射系数；接着根据基于Gordon 积分的板块元方法计算模型的目标强度，并提出了基于光线投射的可见面元判别方法；最后对不同频率(1～40 kHz)、不同入射方位角(0°～180°)时敷设空腔覆盖层与未敷设、敷设等厚均匀覆盖层时的潜艇目标强度进行仿真对比，具体分析敷设空腔覆盖层对散射特性的影响。本文的工作对水下复杂目标敷设空腔覆盖层的声散射特性研究进行了补充。

1 板块元理论

1.1 远场板块元算法

在收发合置并且满足远场条件的情况下，由Kirchhoff近似，非刚性表面复杂目标的目标强度可以表示为[18]

其中：面积分I表达式为

式中：S为目标外表面；k为入射波的波数；rs为面元到参考点的矢量；r0为收发点到参考点的单位矢量；n0为面元的单位法向矢量；θ为面元法向矢量与入射波方向矢量的夹角，R(θ)为声反射系数，对于刚性表面目标R(θ)=1。板块散射示意图如图1所示。

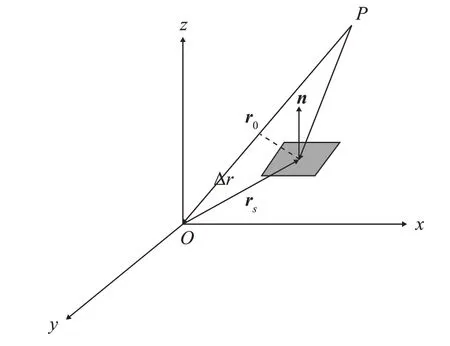
图1 板块散射示意图Fig.1 Schematic diagram of planar scattering

计算远场目标强度关键在于计算面积分I。板块元方法就是一种加快面积分I计算速度的方法。该方法先把目标表面划分成许多小曲面，然后利用平面面元代替曲面面元，最后将各个平面面元的散射声场矢量求和就可以近似得到目标散射声场。据此，远场板块元算法的目标强度计算式可以表示为

其中：m为划分的面元的个数。

1.2 板块元算法的Gordon积分应用

由式(3)可知，板块元算法的计算过程包含了大量对平面面元的积分，要提高计算效率，将面元积分转换为求和是关键。现在常用的方法主要有傅里叶变换积分算法[19]和Gordon积分算法[20]。由于使用傅里叶积分算法简化式(3)时，存在积分分母为0的风险，因此这种算法将出现数值不稳定的问题。然而，将Gordon 积分应用至板块元算法可以成功将面积分简化为求和，并且避免了奇异值的出现，保证算法的稳定性。Gordon积分的公式为

式中：面元s是N边形，其顶点分别为a1，…，aN，且a1=aN+1，并对于1≤n≤N，有面元的n个边矢量Δan=an+1-an。根据洛比达法则，可得：

此时积分有界，该方法具有稳定解。对式(3)中所有的面元积分进行Gordon 积分变换后，可得到用于预报目标强度的基于Gordon 积分的板块元算法计算表达式：

式中：ρn=(an+1+an)/2为面元第n边的中点向量。

1.3 基于光线投射的可见面元判别方法

由Kirchhoff 近似的两个假设可知，声波入射时目标表面可以分为亮区与影区，亮区对声波散射有主要贡献。因此，利用板块元算法计算水下复杂目标声散射时，只有亮区面元对散射有贡献。在目标形状复杂时，还需要考虑并去除面元之间相互遮挡对散射带来的影响[21]。最后，复杂目标的散射声场可近似为所有亮区可见面元散射声场的矢量和。

针对板块元算法在水下复杂目标声散射计算过程中，采用两两比较的可见面元判别方法耗时巨大的问题，本文提出了基于光线投射的可见面元判别方法，可以快速地提供板块元计算所需的可见面元。基于光线投射的可见面元判别方法主要有两个步骤：

(1) 后向面去除。后向面去除通过考察每个面元的外法向量与观察方向的夹角实现，如图2 所示，向量n为面元的外法向量，r为到观察方向的向量，当向量n和向量r的夹角大于90°时，面元判定为后向面。后向面去除可以消除场景中一半左右的隐藏面。

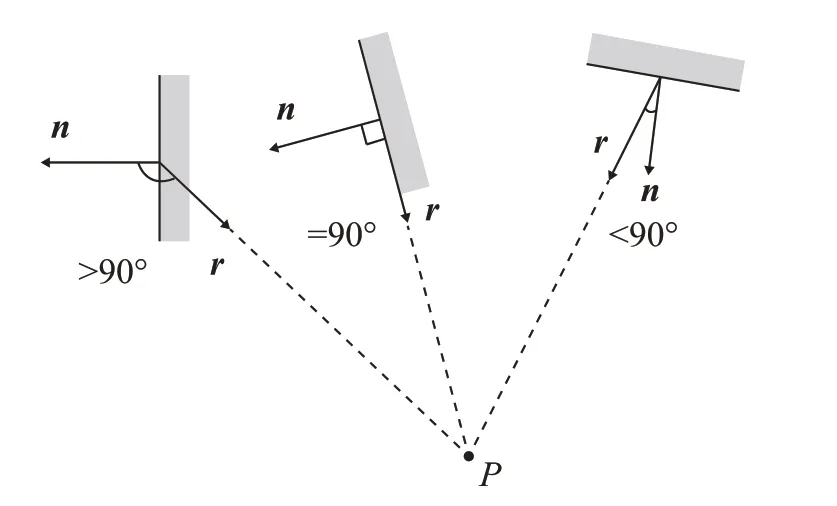
图2 观察方向与法线夹角示意图Fig.2 Schematic diagram of the angle between the viewing direction and the normal

(2) 光线投射消隐。去除后向面之后，仍存在大量的面元，面元间采用两两相互进行遮挡判别的方法计算量大、耗时长。在计算机图形学[22]中，光线投射算法将绘图窗口内每个像素的投影线与场景中所有的多边形求交，如果有交点则使用距离最近的点所属多边形的颜色显示相应的像素；如果没有交点，则使用背景色。本文将光线投射算法的思想引入到模型消隐中，实现对模型网格划分遮挡面的消除，基于光线投射的可见面元判别流程图如图3所示。

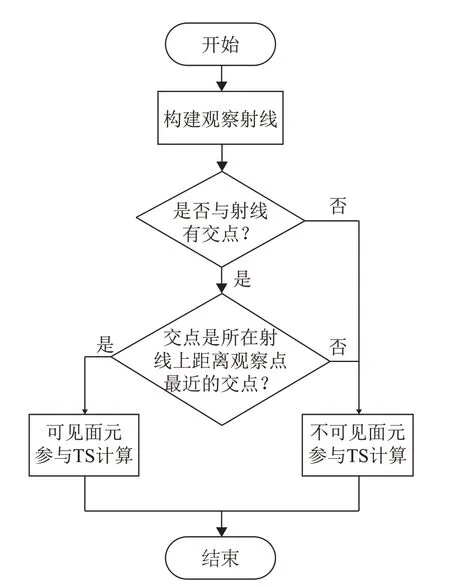
图3 基于光线投射的可见面元判别流程图Fig.3 Flowchart of the visible facet judgment based on ray casting

观察点与模型位置关系示意图如图4所示。从观察点发射具有一定立体角的射线束，这些射线与模型表面划分的面元相交。一条由观察点发射的射线如果只与一个面元存在交点，则该交点所对应的面元表示为可见面元；如果该射线与多个面元存在交点，则距离最近的交点所对应的面元表示为可见面元。所有可见面元的集合，即为观察点观察到的模型可见面元。

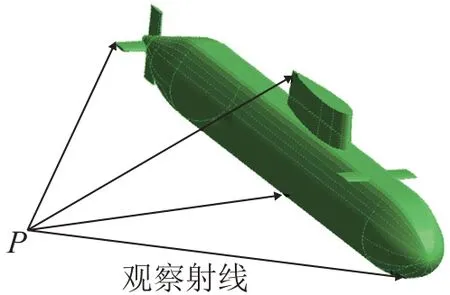
图4 观察点与模型位置关系示意图Fig.4 Schematic diagram of the relationship between the observation point and the model

假设模型有m个面元参与遮挡判别。使用两两比较的方法，需要进行C2m(约m2/2)次遮挡判别计算，需进行3m2/2次点到平面投影计算。使用本文提出的可见面元判别方法，根据发射声线密度系数c的不同，需要进行m/c2次点到面投影计算。在面元数较大时，此方法可以显著地减少计算量。

选取BeTSSi Ⅱ潜艇模型为研究对象，利用基于光线投射的可见面元判断方法对其网格划分后的数值模型进行可见面元判别，声波从不同方位入射时的判别结果如图5所示，根据结果可知，此方法很好地实现了对可见面元的判别。

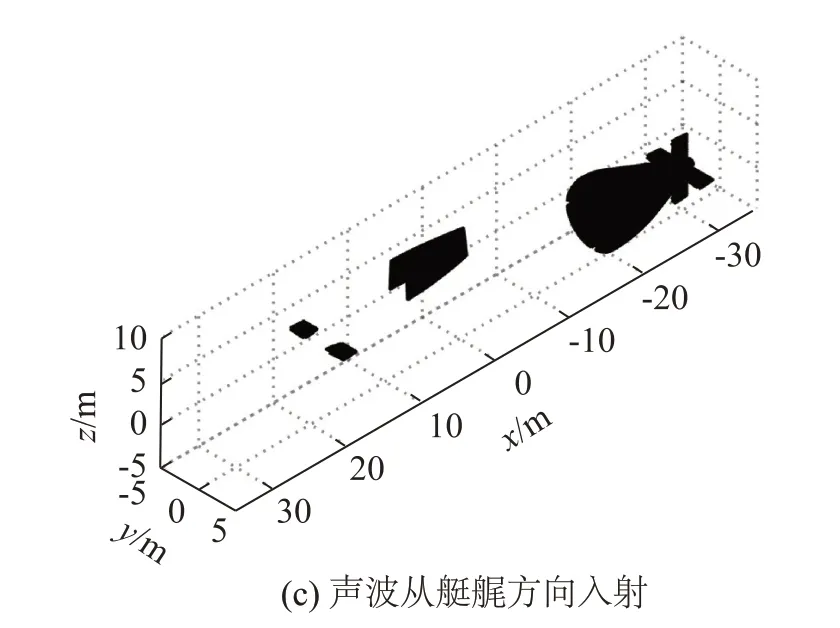
图5 声波从不同方位入射时潜艇的可见面元判别结果Fig.5 Discrimination results of visible facets of submarine when sound waves are incident from different directions

1.4 板块元方法算例校验

为了检验板块元方法的有效性，以典型刚性球为例，分别利用板块元方法和经典解析法进行声散射计算，并比较两种方法的计算结果。取刚性球的球心作为坐标系的原点，并取入射平面波的传播方向为x轴，刚性球散射示意图如图6所示。

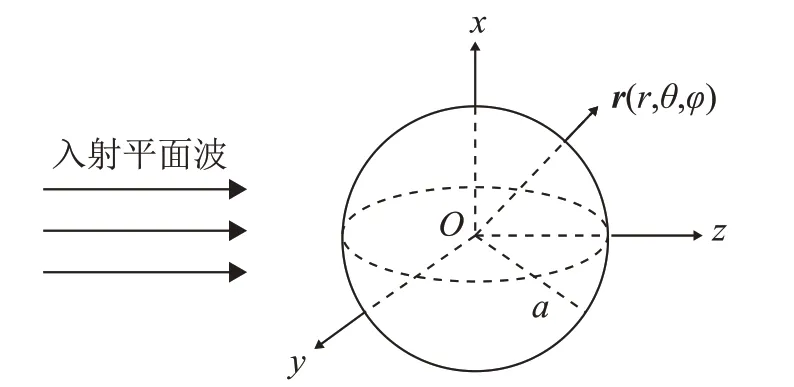
图6 刚性球散射示意图Fig.6 Schematic diagram of rigid sphere scattering

首先对半径a=1 m的刚性球进行几何建模并进行网格划分。刚性球网格划分结果结果如图7所示。

图7 刚性球网格划分结果Fig.7 Meshing result of rigid sphere

刚性球的目标强度如图8 所示。由图8 可知，板块元方法和解析法计算得到的目标强度值相差很小，并且目标强度的大小随频率的增大逐渐趋向一致，证明了应用Gordon 积分的板块元算法在高频时计算目标强度的有效性。

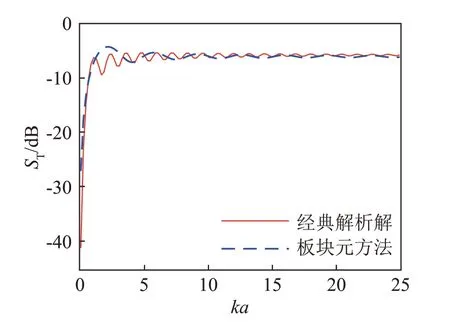
图8 刚性球目标强度Fig.8 Target strength of rigid sphere

2 声反射系数理论计算

2.1 分层等效理论

声反射系数是反映空腔覆盖层声学特性的基本参数，但是变截面空腔覆盖层直接计算存在计算复杂度高的问题，因此通常采用分层等效近似的方法，将变截面空腔等效为多个均匀圆柱空腔[23]。在此基础上利用弹性波传播理论，结合应力连续边界条件求得等效复波数，最后采用传递矩阵法得到敷设空腔覆盖层的目标声反射系数。

变截面空腔覆盖层的空腔分布如图9所示。根据周期对称性，只需取其中的一个单元体进行声学分析。考虑空腔截面大小渐变，采用多个均匀等效等厚圆柱空腔作为近似。根据已有研究可知，当分层的厚度足够小时，这种近似方法具有较好的精度。

图9 空腔周期分布的覆盖层及其简化示意图Fig.9 Schematic diagram of the anechoic coating layer with periodic columnar cavities and its simplification

取分层近似后的1层进行分析，其圆柱空腔层示意图如图10 所示。该圆柱空腔单元的内半径和外半径分别为a、b。

弹性圆柱管柱坐标形式的振动方程[24]为

式中：ur是沿r方向的振动位移，uz是沿z方向的振动位移；λ、μ分别为橡胶的拉米常数和复剪切模量。

考虑到内部空腔，内管壁可视为自由边界，外管壁则需满足法向位移ur和切应力σrz为0，σrr表示介质内正应力。因此弹性圆柱管的声学边界条件为

将振动方程求得的含有未知系数的解代入边界条件，可以解得轴向等效复波数：

其中：

式中：ε=a/b为孔隙率，ρ为橡胶的密度，kl为纵波波数。并且可得等效密度ρeq和等效声速ceq：

2.2 传递矩阵和声反射系数

水下复杂目标如潜艇等多为单层或多层壳体结构，因此在计算声反射系数时常将敷设覆盖层的目标等效为由多层介质组成的复合结构[25]，前界面为无限大水域，后界面为空气。平面波入射到多层均匀结构，其示意图如图11所示。

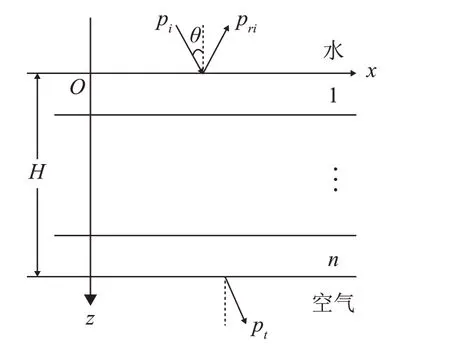
图11 声波入射多层均匀结构示意图Fig.11 Schematic diagram of the acoustic wave incoming into uniform multilayer structure

传递矩阵法[26]是研究多层均匀复合结构声学特性的常用方法。对于每一层介质都可以用一个传递矩阵表示该层相邻两侧声压和质点振速的关系。若将多层复合结构视为一个整体，并采用表示振速分量和应力分量vx、vz、σx、σz在第n层的值，则在复合结构的前后界面各有四个参数，并通过多层结构的传递矩阵连接，表达式如下：

式中：传递矩阵A是一个4×4型的矩阵，其矩阵元素与复合结构各层介质的参数有关，具体取值见文献[27]。

当入射波以角度θ入射时，R为覆盖层的反射系数，入射波Pi和反射波Pr表达式为

当z=0 时，即在复合结构前界面时，边界条件为

当z=H时，即在复合结构的后界面时，近似为自由边界条件：

将式(14)和式(15)代入式(13)，可以求得反射系数R。为便于表示，引入参数：

解出的多层复合结构的声反射系数R可以表示为

式中：Z0=ρ0c0/cosθ0，Zn=ρncn/cosθn分别为入射波所在介质和出射波所在介质的法向声阻抗率。

3 声散射特性仿真研究

3.1 BeTSSi Ⅱ潜艇模型仿真

选取BeTSSi Ⅱ潜艇模型[17]为仿真对象。BeTSSi Ⅱ潜艇艇长为62 m，艇身围壳直径为7 m。潜艇模型如图12所示。按照方位角区分，0°为艇艏方向，90°为正横方向，180°为艇艉方向。

图12 BeTSSi Ⅱ潜艇模型Fig.12 BeTSSi Ⅱ submarine model

在进行数值计算前，利用ANSYS 软件对BeTSSi Ⅱ潜艇进行3D建模，网格划分类型选择Tri(三角形网格)，为了保证计算精度，面元划分尺度与计算频率之间的关系应满足d2/(λ·Rc)≪1 的条件，其中d为面元划分尺度，λ是波长，Rc是目标表面在此面元处的高斯曲率。最后，将潜艇表面划分为89 768个三角形面元，提取得到44 886个顶点坐标。ANSYS潜艇模型网格划分如图13所示。

图13 潜艇模型的ANSYS网格划分Fig.13 Submarine model meshing by ANSYS

3.2 声反射系数的数值计算

为了计算潜艇敷设覆盖层时的声反射系数，对如图14所示的由覆盖层和钢板组成的复合结构进行声学特性研究。复合结构两侧分别是水介质和空气介质。覆盖层的厚度为5 cm，钢板的厚度为2 cm。表1给出了此复合结构相关材料的参数。

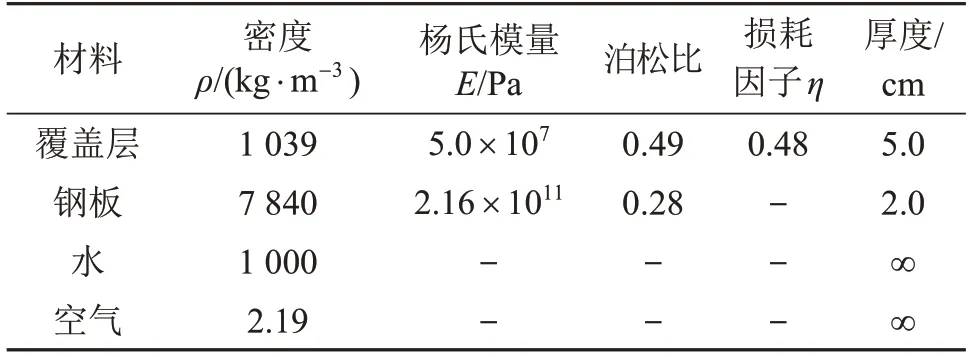
表1 复合结构各层材料参数Table 1 Material parameters of each layer of the composite structure

图14 覆盖层-钢板复合吸声结构示意图Fig.14 Schematic diagram of composite sound-absorbing structure composed of anechoic coating layer and steel layer

采用的空腔覆盖层的结构如图15 所示。空腔覆盖层结构两侧分别是均匀层，中间部分为含圆台型空腔的材料层，腔体左端面直径为5 mm，右端面直径为15 mm，计算的吸声结构单元截面是边长为18 mm的正方形。空腔覆盖层的几何尺寸具体如表2所示。

表2 空腔覆盖层几何尺寸Table 2 Geometric parameters of the cavity structural cover layer

图15 空腔覆盖层结构示意图Fig.15 Schematic diagram of cavity structural anechoic coating layer

在计算敷设空腔覆盖层目标的声反射系数时，根据分层近似法，分层数目越多，计算结果的误差越小。对单层壳体敷设空腔覆盖层分为5、10、15和20 层分别进行计算。声波垂直入射和斜入射时的计算结果如图16所示。

图16 空腔覆盖层分层层数不同时声反射系数近似计算Fig.16 Approximate calculation of acoustic reflection coefficient of the cavity structural anechoic coating layer with different numbers of layers

根据图16中的仿真结果可知，层数为5时的声反射系数曲线有较大偏差，层数为10、15和20三种情况下的声反射系数曲线几乎完全重合。这说明分10 层进行计算时结果已经较好。因此选取层数10对空腔覆盖层进行近似。敷设空腔覆盖层与未敷设覆盖层、敷设等厚均匀覆盖层时复合结构的声反射系数仿真结果如图17～20所示。

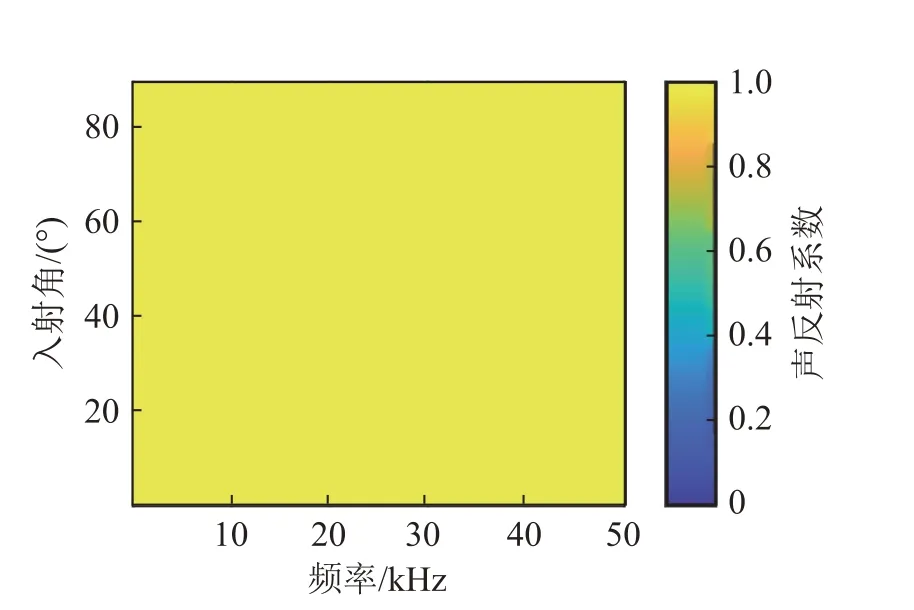
图17 未敷设覆盖层时复合结构的声反射系数云图Fig.17 Acoustic reflection coefficient nephogram of the composite structure without anechoic coating layer

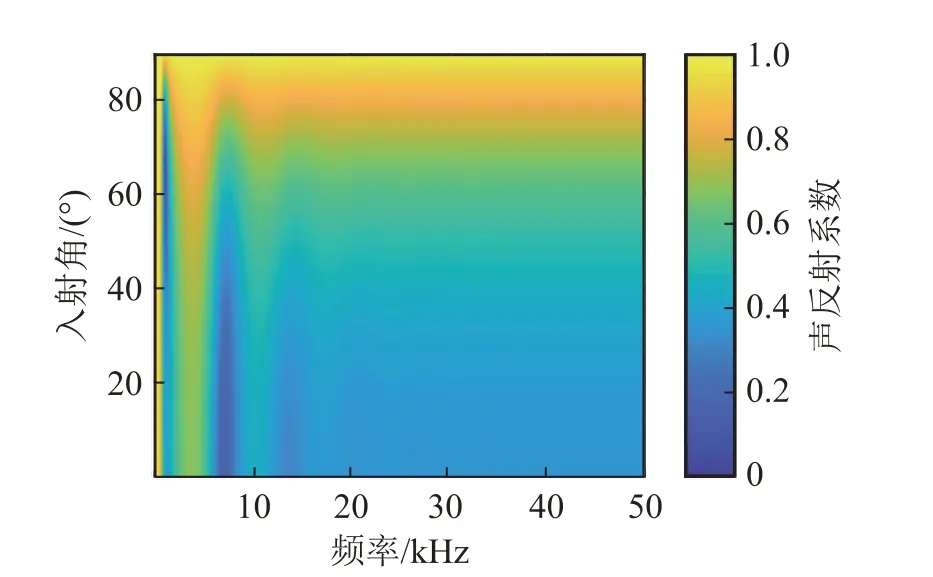
图18 敷设均匀覆盖层的复合结构的声反射系数云图Fig.18 Acoustic reflection coefficient nephogram of the composite structures with uniform anechoic coating layer

图19 敷设空腔覆盖层时复合结构的声反射系数云图Fig.19 Acoustic reflection coefficient nephogram of the composite structure with cavity structural anechoic coating layer

图20 声波垂直入射时不同覆盖层的复合结构声反射系数频响曲线Fig.20 Frequency response curves of acoustic reflection coefficient of the composite structure with different anechoic coating layers under normal incidence of acoustic wave

由上述仿真结果可知：未敷设覆盖层时潜艇模型的声反射系数接近于1。在敷设覆盖层后，复合结构的声反射系数减小，在高频时尤其明显。敷设空腔覆盖层时与敷设等厚均匀覆盖层时相比，声反射系数曲线包络的第一谷值频率降低、频带变窄，第一峰值变大。因此，在频率较低时敷设空腔覆盖层的吸声效果更好。随着频率的增大，两种结构的声反射系数趋于一个相同的稳定值，复合结构的声反射系数与覆盖层的结构没有明显关系。

3.3 潜艇模型声散射特性预报及分析

本节在潜艇几何建模、网格划分和可见面元判别的基础上，结合计算得到的敷设覆盖层后复合结构的声反射系数，利用基于Gordon 积分的板块元方法分别计算敷设空腔覆盖层以及未敷设覆盖层、敷设均匀覆盖层时潜艇的目标强度。为了分析声波频率及入射方位角对敷设空腔覆盖层的BeTSSi Ⅱ潜艇模型声散射特性的影响，仿真声波以频率1～40 kHz、入射方位角0°～180°入射到上述三种情况下的潜艇目标，得到潜艇目标强度方位-频率谱图。结果如图21～23所示。

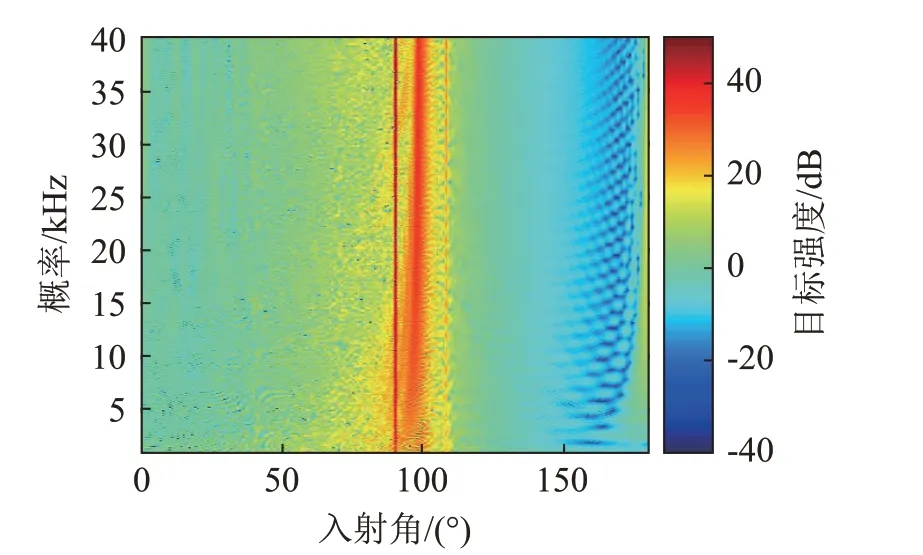
图21 未敷设覆盖层时潜艇目标强度方位-频率谱Fig.21 Azimuth-frequency spectrum of target strength of submarine without anechoic coating layer

由图21 可知，BeTSSi Ⅱ潜艇的目标强度随方位角的变化规律是正横方向附近目标强度值最大，艇艏方向和艇艉方向附近值目标强度比较小，并且在100°附近出现了明显的峰值。当潜艇的方位发生变化时，各部位对声散射的贡献发生变化，这使得潜艇目标强度随方位发生变化。对此，可以解释如下：在100°附近潜艇的艉部起到了较大的贡献；在艇艏和艇艉方向附近，潜艇散射截面较小，目标强度较小；在正横方向附近，潜艇散射截面较大，目标强度较大。

对比图22、23 与图21 可知，敷设覆盖层可以降低目标强度，但是不同频率下效果不同。由于在正横方向目标散射截面比较大，目标强度也比较大，因此进一步研究正横位置的目标强度可以更好地分析潜艇目标声散射的频率特性。敷设不同覆盖层潜艇正横位置目标强度频率响应如图24所示。

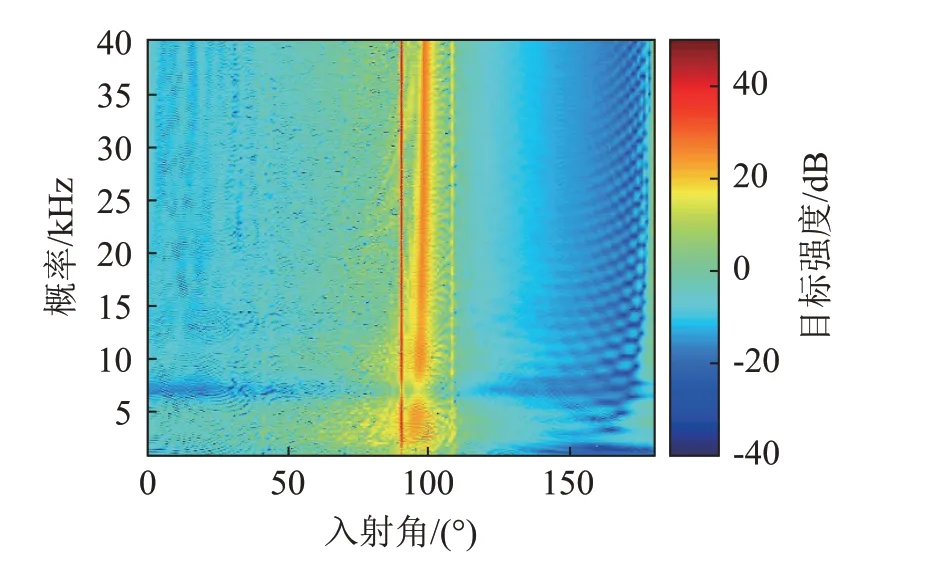
图22 敷设均匀覆盖层时潜艇目标强度方位-频率谱Fig.22 Azimuth-frequency spectrum of target strength of submarine with uniform anechoic coating layer

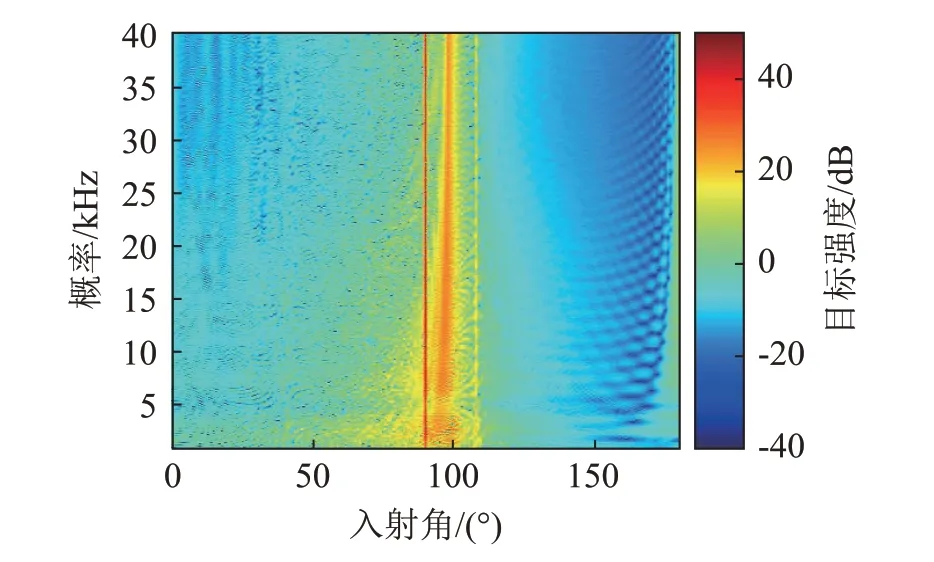
图23 敷设空腔覆盖层时潜艇目标强度方位-频率谱Fig.23 Azimuth-frequency spectrum of target strength of submarine with cavity structural anechoic coating layer

图24 敷设不同覆盖层的潜艇正横位置目标强度的频率响应曲线Fig.24 Frequency response curves of target strength in abeam position of the submarine with different anechoic coating layers

通过比较分析敷设空腔覆盖层和敷设均匀覆盖层两种不同情况下潜艇正横位置附近目标强度值可以看出，选取本文给出的覆盖层结构和参数的，在频率1 kHz附近敷设空腔覆盖层时正横位置目标强度比敷设等厚均匀覆盖层时更小。这表明在频率较低时敷设空腔覆盖层的吸声效果较好。在2～23 kHz频段内，两种情况下潜艇正横位置的目标强度起伏变化，但总体上敷设均匀覆盖层时的正横位置目标强度较小。当频率大于23 kHz，敷设覆盖层时的正横位置目标强度相比未敷设覆盖层时降低了约10～12 dB，并且敷设空腔覆盖层时的正横位置目标强度相比敷设等厚均匀覆盖层时较小。综上可知，在频率较低时敷设空腔覆盖层有助于进一步减小目标强度，随着频率的增大敷设空腔覆盖层的吸声性能与敷设等厚均匀覆盖层的吸声性能起伏变化，逐渐趋于一致。

4 结 论

本文利用基于Gordon 积分的板块元方法对敷设空腔覆盖层的水下复杂目标进行了声散射特性研究，并提出了基于光线投射的可见面元判别方法。在此基础上，以BeTSSi Ⅱ潜艇为例，通过对比敷设空腔覆盖层与未敷设覆盖层、敷设等厚均匀覆盖层时的目标强度方位角-频率谱的差异，讨论了敷设空腔覆盖层对声散射特性的影响。本文得出如下结论：(1)本文提出的基于光线投射的可见面元判别方法在面元数较大时可以显著地减小计算量，可以快速有效地提供板块元方法所需的可见面元。(2)基于Gordon 积分的板块元方法对BeTSSi Ⅱ潜艇的预报结果能够很好地反映其目标强度的特征及其变化规律，具有稳定性和高效性。(3)潜艇敷设覆盖层可以有效降低目标强度，与敷设等厚均匀覆盖层时相比，复合结构声反射系数曲线的第一谷值频率降低，在频率较低时敷设空腔覆盖层的吸声效果更好，可以进一步减小目标强度值，但是随着频率的增大时，敷设空腔覆盖层的吸声性能逐渐与敷设等厚均匀覆盖层时趋于一致。