一种带有附加记忆策略的改进教与学优化算法

陈怡君,任春年,党妍洁,李会荣

(1.西安航空学院 图书馆,陕西 西安 710077;2.商洛学院 数学与计算机应用学院,陕西 商洛 726000)

0 引 言

群体智能优化算法是通过模拟生活中的自然现象或某些动物、植物群体间的竞争、协作进化等行为,实现对优化问题的求解,目前已经受到国内外许多研究者的广泛关注[1-6]。例如,遗传算法模拟了生物界“适者生存,优胜劣汰”达尔文进化论观点[1];粒子群优化算法模拟鸟类的觅食行为,通过群体中个体之间的协作和信息共享来寻找最优解[2];人工蜂群算法模仿蜜蜂的觅食行为[3],模拟退火算法模拟物理系统退火过程提出的一种智能算法等等[4],这些算法目前已经应用于数据聚类、生物医学、电力优化等多个工业或学术领域[2-6]。

Rao等人于2011年模拟课堂教学过程提出了一种新的优化算法,即教与学的优化(Teaching Learning Based Optimization,TLBO)[7]。TLBO工作的基本原理在于教师对学习者在课堂上的输出的影响,学习者的表现是由他学习到的结果或学习成绩来衡量的,教师扮演着知识传授者的角色,经验丰富的老师能够培养出更好的学生。算法可分为教学阶段(Teaching Phase)和学习阶段(Learning Phase)。教学阶段是指向最好的学生学习,学习阶段是指通过互异学习者之间的互动、讨论进行学习,学习者学习的越多,解决方案就越好。该算法具有参数少、易于编程、收敛速度快等优点,已经成功应用于函数优化、机械优化、车间调度、资源分配等实际问题中[8-13]。例如,Wan等人将优等生与差等生的区别对待进行分班,认为课堂教学行为是小班级教学并行,优等生在一个班级,差生在一个班级,优等生班级和差生班级是动态流动的[14]。侯景伟等人认为学生是可以通过课外辅导巩固知识的,每次教师教学表现可能是不一样的,学生每次学习知识的接受程度也是不一样的,借此提出了动态非线性自适应教学因子、课外辅导因子、动态自适应学习因子等随机线性变化的改进TLBO算法[15]。李子扬等人认为教师也可以自学的,将TLBO的经典两阶段扩充为教师自学阶段、教学阶段和学习阶段三个阶段,使得教师也在算法每次迭代循环中有改进提升机会,但在提升优化性能的同时引入其他算子,提高了算法的复杂度[16]。何杰光等人创造性地认为学生在一轮学习阶段并不仅仅向另一个学生学习,也可以在一轮学习阶段向其他多位同学学习,然后再选择与多位同学知识流通的平均值或最大值作为学到的新知识[17]。此外,王滔等人从学到知识的层面出发,认为当前适应度值大,下次迭代时教学因子就小,当前适应度值小,下次迭代时教学因子就大[18],即表明本次教学效果好,下次迭代时教学程度就低些,本次教学效果差,下轮迭代时教学程度就高些,这样可以在一定程度上防止过拟合或早熟。而康佳惠等人将TLBO算法与其它群体智能优化算法相结合,利用其它智能优化算法中的优势来提高TLBO算法的性能,例如将回溯搜索算法和轮盘赌选择机制引入TLBO以提高TLBO的全局搜索能力和收敛精度[19]。文献[20]引入自适应教学因子和教师的反馈意见对学生学习的影响来提高TLBO算法的学习性能。总之,以上TLBO算法的改进策略在一定程度上提高了算法的性能,并且已经取得了广泛的应用。

但是,以上对TLBO改进的算法中几乎没有考虑到知识记忆过程对当前学习的影响,同时历史知识对学习当前知识的启发也很有帮助。为了弥补这一缺陷,基于学习记忆策略,该文提出了一种带有附加记忆策略的教与学优化(MTLBO)算法。该算法在教学阶段增加了一个学习过去知识的记忆过程,同时学习当前知识和历史知识可以提高学习产出;在学习阶段引入了多个学生学习的策略,提高了算法的搜索能力。在多个基准测试函数的实验结果表明,MTLBO算法在性能上优于其比较算法。

1 基本教与学优化算法(TLBO)

基本TLBO算法主要依靠教师对学习者在课堂上输出的影响,不断提高学习者的学习水平。主要分为教学阶段和学习阶段,基本过程如下。

1.1 教学阶段

(1)

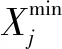
(2)

1.2 学习阶段

在学习阶段,学习者会通过两两互动交流认识自己的差距,并以此提高自己的知识水平。对于第k个学习者Xk来说,更新机制如下:

(3)

一直重复上述步骤直至达到最大迭代次数或者停止准则时,算法停止,输出最优个体。

2 一种带有附加记忆策略的改进教与学优化算法(MTLBO)

2.1 考虑历史知识记忆的教学阶段

标准TLBO算法是一种基于当前状态改进搜索点的优化算法,并没有考虑到学生的历史记忆知识。一般情况下,学生的历史状态知识对当前状态的学习能力的影响同样重要,能够反映现实班级教学行为,教师会要求学生课后练习,复习所学知识,提高学习能力,同时并预习下一次新课;教师也会根据学生的学习情况动态调整新课教学内容与教学方法,提高班级的整体学习水平。因此学生的历史记忆知识与教师历史教学能力对提高班级的整体教学水平具有重要的作用。

所以,在基本的教学优化算法中引入教师历史记忆知识,即在每次更新学习者的同时均要同时考虑教师上一代的最优值和当代的最优值,则第t代教师的知识水平更新为:

w=(t/T)2

(5)

其中,Teacher(t)是第t代的教师,Xbest(t-1)和Xbest(t)为第t-1代和第t代的最优学生,j是维度;w为权重因子,决定着教师上一代知识水平对下代学习能力的影响程度。权重w越大,教师历史记忆知识对当前的影响越小。

2.2 改进的学习阶段

由式(3)可以看出,标准TLBO算法学习阶段主要通过学习者与最优个体之间互动交流而提高自己的知识水平,然而只局限于两个学生之间的互动交流,并没有考虑到班级内最优学生、小组学习、互动学习等学习方式的带动作用。因此,将班级最优学生、随机学习策略引入到学习阶段中,则将学习阶段的迭代方程更新如下:

α=1-(1-t/T)(2·t/T)

(7)

β=(et/T-1)/(e-1)

(8)

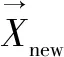
2.3 MTLBO算法实现流程

步骤1:设置最大迭代次数Tmax、空间维数D、种群规模N,设置当前的迭代次数t=1,并初始化种群X,计算班级内个体的适应度f(X)。

步骤2:根据式(2)和式(4)更新教学阶段个体。

步骤3:计算班级内个体的适应度f(X),并使用贪婪策略更新学生个体。

步骤4:根据式(6)更新学习阶段个体。

步骤5:设置迭代次数t=t+1,返回到步骤2,直到t达到设定的最大迭代次数Tmax,输出全局最优值。

3 结果与分析

3.1 测试函数

为了验证所提MTLBO算法的性能,与基本的教学优化算法(TLBO)[21]、一种多反向学习的教与学优化算法(MOTLBO)[17]和具有动态自适应学习机制的教与学优化算法(DSLTLBO)[22]进行对比。选取6个标准测试函数进行实验,其中f1-f5是单峰测试函数,可以测试算法的收敛速度与精度,f6是多峰测试函数,可以测试算法逃出局部最优值的能力。测试函数的表达式、搜索空间信息如表1所示。

表1 测试函数的性质

实验设置如下:班级学习人数均为N=50,最大的迭代次数均为Tmax=300。为了测试算法对复杂高维优化问题的寻优性能,分别在空间维数为30维、50维和100维进行实验,每种算法独立运行30次。30次运行的实验结果的最优值、最差值、平均值和标准差如表2～表4所示。

表2 在空间维数D=30下的测试结果对比

3.2 结果分析

从表2中可以看出,所提MTLBO算法无论从最优值,还是从平均值、方差等方面都优于TLBO、MOTLBO、DSLTLBO算法。由于F6函数是很难优化的复杂函数,原因在于这类函数的局部最优点数目随函数的维数的增加而呈指数增长,因此找到全局最优点极为困难。但是从实验结果看,对于F6函数四种方法均陷入局部最优,对于F5函数,三种算法均没有达到了最优值,但MTLBO算法最优值和平均值均优于其他三种算法,从而表明所提MTLBO算法是有效的。

表3为在50维下30次独立实验的最优值、最差值、平均值和标准差的实验结果。由表3可知,对于函数F1、F2、F3和F4,所提MTLBO算法极大程度地优于其它三种算法,而对于F5函数,四种算法的结果均值都相差不大,但是所提MTLBO算法的最优值和平均值相对较小。

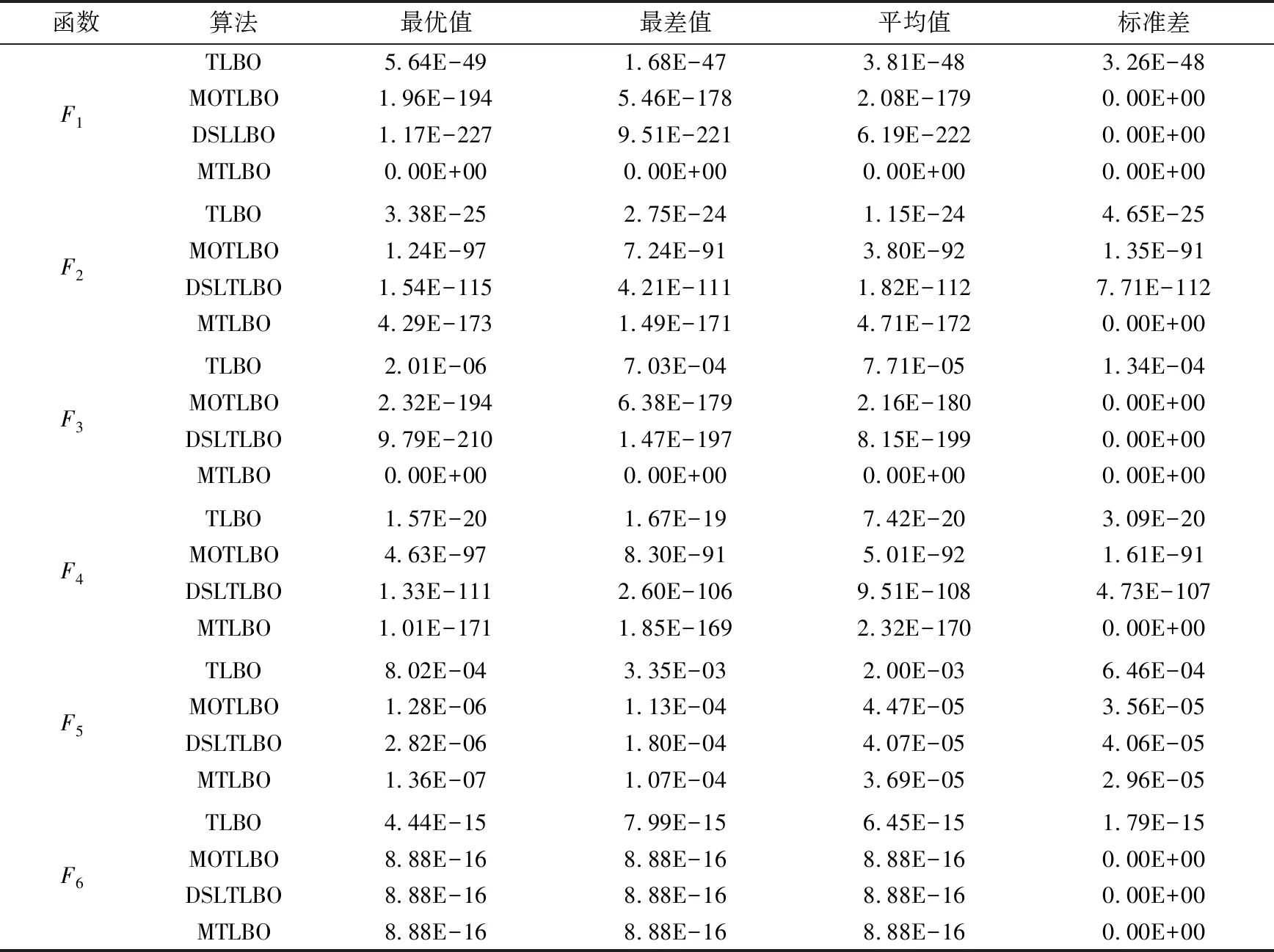
表3 在空间维数D=50下的测试结果对比

为了测试所提MTLBO算法在高维数据上的性能,将搜索空间的维数增加到100维,表4是在搜索空间的维数扩大到100维每种算法的测试实验结果。从表4可以看出,除过测试函数F6外,所提MTLBO算法在最优值方面均优于TLBO、MOTLBO、DSLTLBO算法,同时,标准差相对比较小。对于F5函数,虽然四种算法都没有达到最优值,但是所提MTLBO算法在最优值和平均值上略优于其他方法。对于测试函数F6,四种算法均陷入局部最优,均值都相差不大,除过TLBO算法均在同一个数量级。因此,所提MTLBO算法在高维数据上具有良好的寻优性能。

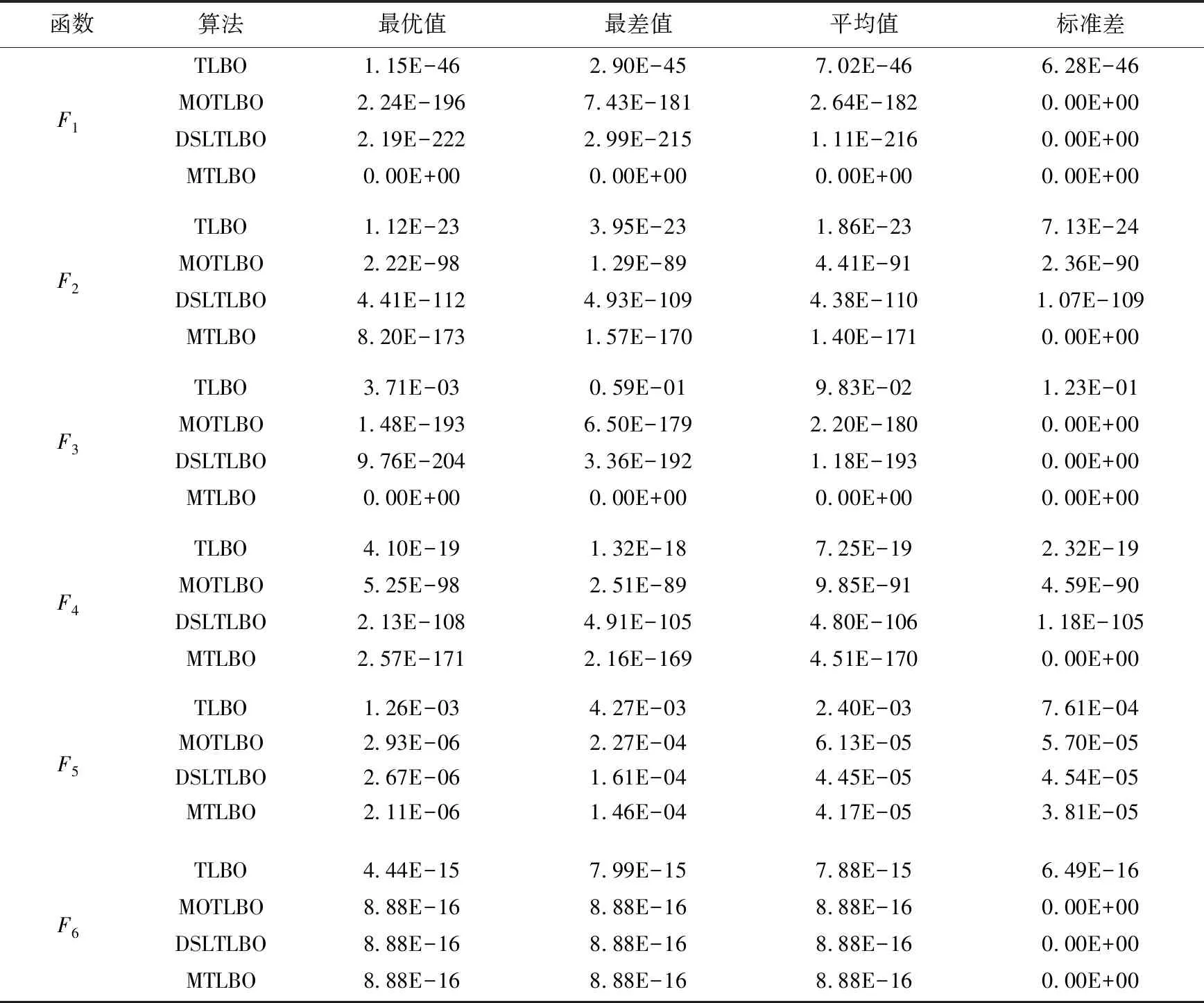
表4 在空间维数D=100下的测试结果对比

图1为函数最优值随着迭代次数的进化曲线。由图1可知,所提MTLBO算法能够跳出局部极值点,具有较快的收敛速度。主要是由于MTLBO算法不但在教学阶段增加了记忆策略,而且在学习阶段引入了个体向最优个体和随机个体学习策略,保持了种群的多样性,提高了算法的性能。从图1(a)和图1(b)中可以看到,所有方法几乎都是梯度向下的趋势,但是所提MTLBO算法收敛速度是最快的。在图1(e)中,各算法收敛性能的差距相对来说并不大,但仍然能看出MTLBO算法具有较优的收敛性,随着迭代次数的增加,MTLBO算法优于其他三种算法;而在图1(f)中,DETLBO虽收敛最快,但其收敛结果并没有达到理论最优值,与其他三种算法的最终结果均相同,但是相比之下,所提MTLBO算法收敛速度是最快的。

图1 函数值随着迭代次数的进化曲线

综上,通过表2～表4与图1可知,无论搜索空间是低维的还是高维的,MTLBO算法在寻优性能上都优于TLBO、MOTLBO、DSLTLBO算法,再一次表明MTLBO算法适用于求解中高规模复杂优化问题。

4 结束语

为了克服教与学优化算法后期局部收敛现象,在TLBO算法教学阶段增加记忆策略,且考虑到学习阶段的学习者不仅仅会向最优个体进行学习,还会向其他学习者学习;在学习阶段增加随机学习策略,提出了一种带有附加记忆策略的改进教与学优化(MTLBO)算法。数值实验表明,MTLBO算法能有效避免局部收敛,提升了算法的寻优性能。

目前,教与学优化算法的应用领域有待进一步拓宽。就工程优化及自动化领域而言,问题的多极小性、多约束性、离散连续变量共存,非线性、多目标性、不确定性等复杂性普遍存在,因此教与学优化算法在该领域的研究应用及其适应性改进仍是一个很有前景的研究方向。