扇形喷嘴参数与雾场均匀度影响研究

沈正昊,丁国清,陈 欣

(上海交通大学 电子信息与电气工程学院, 上海 201100)

0 引言

扇形喷嘴以其搭建简单、雾化效果好、喷射压力大的特点,在农药喷洒[1]、喷雾清洗[2]以及喷雾冷却[3]等场合得到广泛使用。扇形喷嘴喷射的雾场为扇形,单次喷洒在被喷洒面上会形成如长椭圆形的喷洒区域,这种特殊的喷洒形状对于多次喷洒流量均匀分布具有积极意义。

为了提高扇形喷嘴的应用效率,选择符合需求的喷嘴,对于雾化的理论与应用的研究也在不断地发展。目前对于雾化喷嘴的研究方向主要有以下2个方面:一是雾化机理方面,主要研究液体在液膜或液柱的形态下与空气相互作用,产生一次碎裂与二次碎裂的机理,进而对液滴雾化半径、大小、半径分布等多种参数进行理论研究;二是喷嘴优化方面,主要针对喷嘴的流量、雾化角以及雾化均匀性等方面对喷嘴性能进行优化,使喷嘴更加符合工业需求,而优化的主要方式为改变喷嘴孔径、切槽角、相对切深等扇形结构参数。研究方式包括通过实验平台与对应仪器(高速摄影、相位多普勒粒子分析仪等)获取数据进行研究以及基于CFD(computational fluid dynamics)仿真计算对雾化喷嘴的内外流场进行仿真计算研究。

在雾化喷嘴破碎机理方面,整体的破碎机理已经有了比较完备的研究,对于液滴破碎与湍流动能、液体密度以及液体黏度等特性对液滴破碎的影响已经有了较完备的研究。至今,针对破碎模型仍在不断补充与修正,如程会川等[4]研究韦伯数对雾化喷嘴一次破碎影响规律,Khezzar等[5]利用高速摄影及相位多普勒风速仪对水-空气射流雾化器喷雾的平均液滴尺寸和速度分布进行了测量。

由于喷嘴优化与生产实际具有很强的关联性,因此对这一方面的研究也是目前的主流,且在实验研究与仿真计算研究2个方面都有较为深入的探究。如在实验方面,Wei等[6]通过实验的方式探究了喷嘴的液滴尺寸、压力与流量等参数,刘冬梅等[7]对扇形喷头的结构与压力对雾滴分布及活性的影响进行了研究。在CFD仿真计算领域,由于计算机计算性能的提升,基于有限元仿真计算喷雾流场的研究也在不断进行,陈雁等[8]使用欧拉-欧拉法对喷枪的喷涂流场性能进行了研究,侯俊花[9]使用仿真计算与实验验证的方式研究了喷嘴形状对于喷嘴性能的影响。

然而,目前对于喷嘴性能优化的研究主要集中在改善雾化质量、改变雾化角度及研究雾化液滴的直径分布等内容,对于如何改善喷嘴的雾场分布仍较有限。目前主流的观点认为,扇形喷嘴的雾场分布一般有均匀分布与近高斯分布2种情况。然而在实际使用中发现,喷嘴的雾量浓度分布与主流观点以及厂家提供的信息具有差距,最后产生的结果为具有三峰的流量分布,而非均匀或类似高斯分布。在研究与使用过程中,这种流量分布已经被研究人员所发现[10],且研究人员发现出现这种分布与喷嘴自身参数具有关联性,然而对于喷嘴参数如何影响雾场流量的分布,如何得到更均匀的扇形喷嘴的研究仍然很少。这一现象产生的可能原因有:

1) 对于扇形喷嘴的应用场合,目前的均匀度已经可以支撑实际生产,现有的模型具有一定误差。

2) 目前主流的研究都基于喷雾的速度场与粒径研究,速度场与粒径分布具有较高的均匀性。

3) 若需要足够均匀分布的喷嘴,则有性能更好的其他喷嘴类型选择。

使用CFD仿真计算,对影响喷嘴雾场分布的喷嘴参数进行了研究,以提高扇形喷嘴雾场流量分布的均匀性,对改进喷嘴均匀度具有指导意义。

1 喷雾原理

1.1 碎裂模型

在工业生产与日常生活中,喷嘴已经发展出多种品类,例如生活中的花洒、喷雾罐以及工业中的各种喷嘴。从使用方式上来讲,喷嘴的喷雾方式主要包括单相喷嘴以及两相喷嘴。无论是单相喷嘴还是两相喷嘴,其雾化的原理具有一致性,主要靠喷嘴喷射出液体后与空气之间的相互涡流作用,最终打碎成细小的液滴,实现喷雾的功能。而两相喷嘴的空气相具有更大的能量,从而能将液体撕裂[11]。

从雾化形式上讲,雾化一般认为有圆射流破碎雾化与液膜破碎雾化2种类型。喷嘴喷出的实心液体柱被称为液体圆射流。当圆射流从喷嘴连续喷出时,其与外界气体相互作用,从而在表面形成一定模式的振动波。振动波振幅会逐渐增大,当超过液体表面张力时会碎裂成液片和大颗粒的液滴。

液膜破碎雾化根据喷嘴类型可分为平面液膜和环形液膜[12]。与圆射流类似,当液膜射流从喷嘴喷出后,与周围空气相互作用,导致液膜表面形成振动波,振动波振幅逐渐增大,最终碎裂成液滴。York等[13]对平面液膜的破碎机理进行了理论和实验研究,认为液膜表面波的波长、频率、气体的流动速度、液膜的表面张力以及气液密度都会影响液膜的碎裂,其碎裂半径如下:

(1)

式中,qm为液体的质量流量; ΔP为喷射压力与环境气体背压之差;σl为液膜表面张力系数;ρg为环境气体的密度。

而液膜破裂为雾滴的时间为:

(2)

1.2 扇形喷嘴喷雾原理

扇形喷嘴是一种平面液膜喷嘴,最终产生窄椭圆形或窄矩形的雾流,如图1所示。这种喷嘴是由撞击式喷嘴演化而来的[14]:当两股直径和流速相等射流以不小于90°的夹角碰撞时,在碰撞的位置会产生扇形平面液膜,实现喷嘴雾化,如图2所示。扇形喷嘴的特殊结构能够在喷嘴内部实现类似的射流碰撞效应,从而在喷嘴出射口实现扇形液膜。相比于圆射流原理的雾化喷嘴,扇形喷嘴流量范围大、雾化角范围大且低压下雾化性能好,具有很大的优势。

图1 扇形喷嘴喷射雾流示意图

1.扇形喷;2.圆射流喷嘴

1.3 雾场分布参数

1) 雾化锥角。雾化锥角是指2个喷雾弧的切线之间的夹角,反映了雾化喷嘴能够喷射的最大范围。雾场分布会受到喷射范围的影响,均匀度和流量也有一定影响。

2) 流量分布。流量表示某一位置流过液体的瞬时流量,是整个雾场分布的基础,是实际生产中关心的参数,决定了最终喷洒的均匀度。

2 喷嘴流场计算域与网格划分

计算域模型与网格划分是仿真计算准确的基础,较为稀疏的网格划分能够加快计算的速度,提高运算的效率,而相对应的是可能会造成结果精度上的误差;较为密集的网格划分能够保证计算结果的精度,而相对应的是运算设备的负荷相对较大。

2.1 内流域模型

扇形喷嘴结构如图3所示,结构参数如表1所示。

表1 扇形喷嘴结构参数

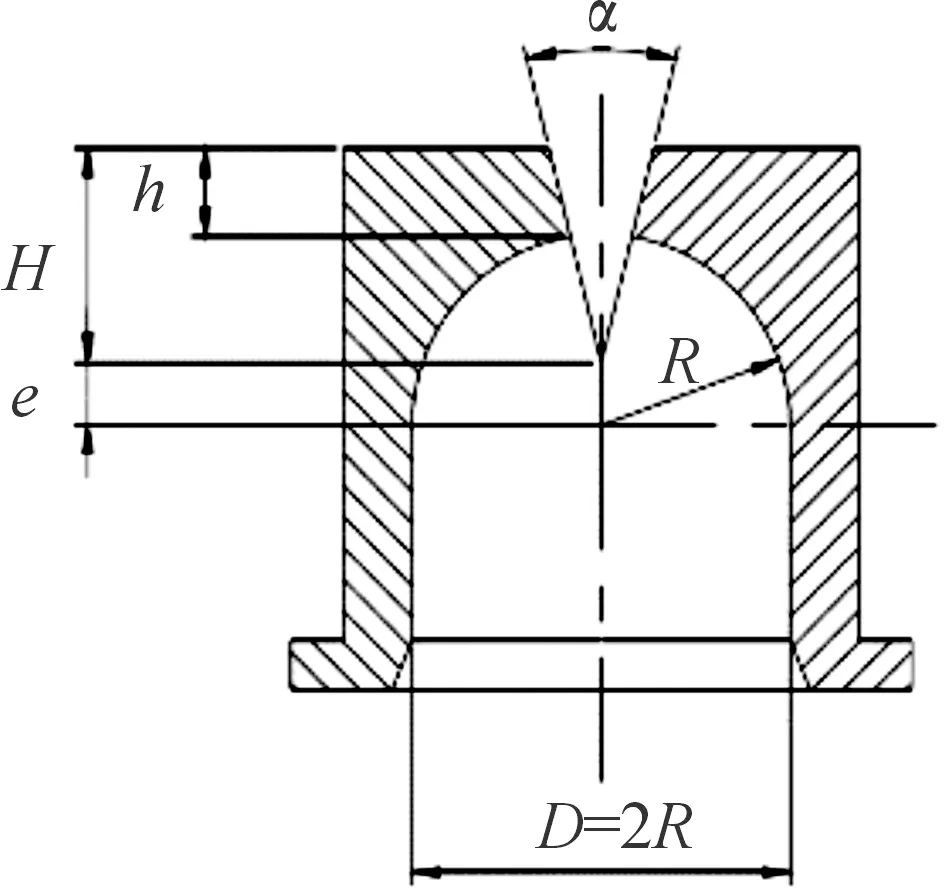
图3 扇形喷嘴结构设计图

基于上述参数对喷嘴的内部流场模型使用Design Modeler(DM)进行了模型搭建,该结构为流场仿真计算域,如图4所示。

图4 扇形喷嘴内部流场模型

2.2 外流场与区域划分

外流场将直径50 mm、高度50 mm的区域作为计算域,同时喷嘴与外流场之间还有一段连接域,在该连接域将实现两股射流的碰撞,形成扇形液膜。最终得到的扇形喷嘴及过渡区域与外流场如图5所示。

图5 扇形喷嘴及过渡区域与外流场

基于仿真计算与后处理的需求,对内外流场计算域进行区域划分,结果如图6所示。Inlet为液体注入口,其作用为向喷嘴内部进行喷射。Wall为壁面,具有阻挡流体的作用,在计算过程中将计入该壁面的影响。其余壁面都被设置为Outlet,为计算出口,软件会计算该位置为开放域。Air空间域为外部的部分流场域,为后处理分析的主要区域。Puz空间域为喷嘴内流场影响的主要区域,在该区域内部流速以及流量大小与Air域有很大的差距,因此与Air域分离计算。

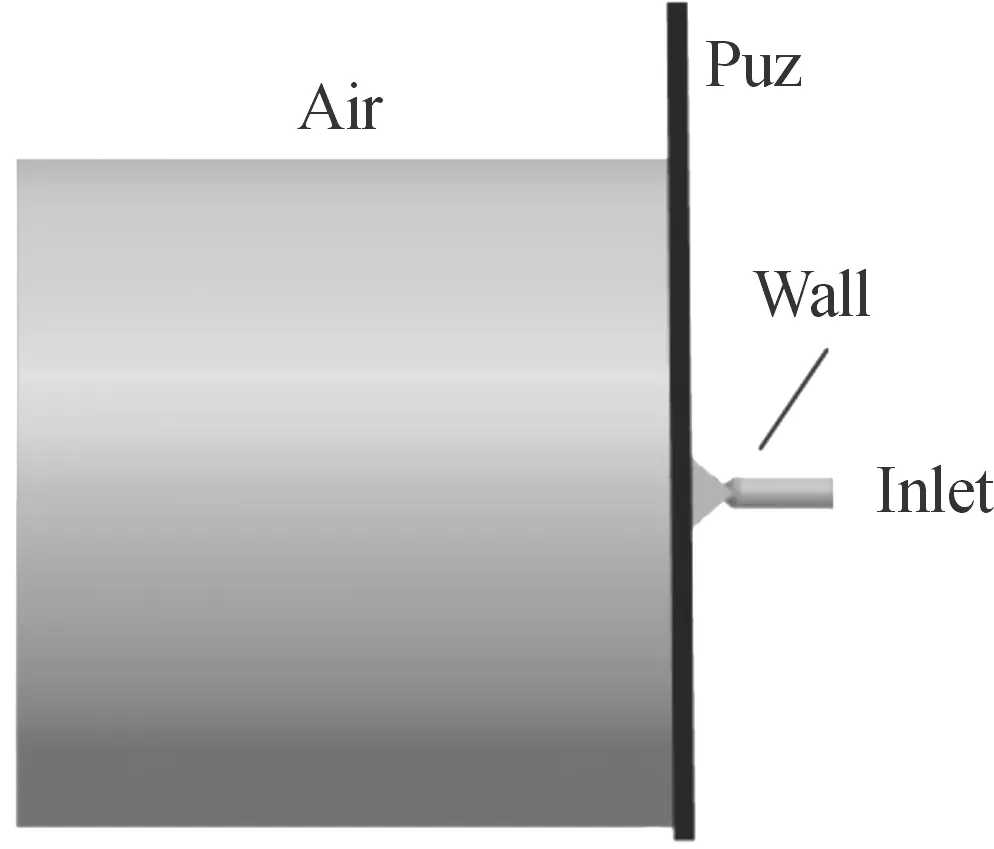
图6 内外流场区域划分示意图

2.3 网格划分

过密的网格会加大计算量,从而导致计算的收敛性较差[15]。网格划分的原则为在复杂计算的位置进行较密集的网格划分,而在简单计算的位置进行较稀疏的网格划分,中间过渡阶段实现网格从密到疏的过渡。

2.3.1 网格加密

在喷嘴内部与喷嘴射出后的外流道处,液流互相碰撞并扩散,从而产生具有扇形形状的雾场,是液流快速变化的区域,因此该部分需要人为手动进行加密处理。Meshing软件的加密功能能够在被加密区域形成足够的有限元,确保被计算区域的精度。模型中,在喷嘴孔径内能够生成尺寸小于孔径1/10的有限元网格,保证液流流动的准确性。

2.3.2 网格质量

网格偏度是评价网格划分好坏的重要标准[16],表示了单个有限元网格相较于标准网格的偏移量,是一个0～1的数字,越接近1则代表该网格质量越差。

在最终划分结果中,绝大部分网格的偏度在0.14～0.5的范围内,平均偏度为0.254,最大偏度为0.91,最小偏度约为0,满足网格质量要求。

2.3.3 网格尺寸

网格尺寸代表网格基本单元的尺寸长度。为了验证网格无关性,分别选取0.5、1、1.5、5 mm尺寸的网格,根据基础模型进行仿真计算,获得喷雾流场的容积分布云图,如图7所示。

图7 仿真计算容积分布云图

使用5 mm尺寸网格的仿真结果与另外3种尺寸网格相差较大,因此并不能使用5 mm尺寸网格。将网格尺寸从1.5 mm一直减小到0.5 mm,得到的仿真结果变化不大,同时0.5 mm尺寸与1 mm尺寸的网格仿真结果的变化已经较小,继续提高网格的精细程度会造成计算结果难以收敛、计算时间较久的问题,因此综合考虑计算性能后,将1 mm尺寸的网格作为研究使用的网格尺寸。最终的网格划分结果如图8所示。

3 数值求解

3.1 湍流模型

湍流模型使用Realizablek-ε模型进行模拟计算。在Realizablek-ε模型中,会对k与ε两个变量进行计算,与之对应的运算方程为[17]:

Gb-ρε-Ym+Sk

(3)

(4)

式中,Gk由平均速度梯度引起的湍动能产生;Gb由浮力影响引起的湍动能产生;Ym为可压缩湍流脉动碰撞对总耗散率的影响;C1ε、C2ε、C3ε为经验常数,分别取1.44、1.92、0.09;σk、σε为湍动能和湍动耗散率对应的普朗特数,分别取1.0、1.3。

3.2 两相流基本控制方程

质量守恒方程为:

(5)

式中,下标q为g和d时,分别表示气相和液相;αq为相体积率;νq为q相的速度(m/s);ρq为q相的密度(kg/m3)。

动量守恒方程为:

-αq▽p+▽τq+αqρqg+Ftd,q+Fq

(6)

式中,τq为q相的粘性应力(N/m2);p为相共用的压力(N/m2);g为重力加速度(m/s2),Ftd,q为q相的单位体积湍流分散力(N/m3);Fq为单位体积相间作用力(N/m3)。

3.3 模拟条件和参数设定

对扇形喷嘴模型在正常使用过程中的雾量均匀性进行研究,其中需要考虑重力因素,静止时充满空气,模型基于水相与气相之间的相互作用进行计算,因此求解模型设置为两相流模型。整个求解时间设定为0.01 s,仿真实验结果显示该时间下整个动态仿真模型能够达到稳定喷射状态,进入稳定喷射状态后的后续状态不会产生较大幅度变化,接近于实际生产过程的喷射状态,同时尽可能简化计算步骤,减少计算量。

将仿真模型Inlet表面设置为压力入口界面,射入物质设置为100%水,其他位置设置为初始0%水,对应100%空气。外流场的Outlet边界设定为压力出口,且均采用escape边界条件。

数值计算结束后,软件将保存计算结果,使用后处理软件CFD-POST即可对数据进行深入的可视化处理。使用CFD-POST中的自定义公式功能,对喷洒平面上的雾量流量进行计算,计算式为:

Qw=Fraw×Vw×d

(7)

式中,d为扇形长轴方向上有限元的宽度;Fraw为该有限元内水的占比;Vw为该有限元计算得到的整体流速。

初始设置模型喷射压力为0.3 MPa,接口形状为球形。有限元计算基于ANSYS Fluent商业软件,计算方法为有限体积法,基于Windows 64位操作系统的12核心Xeon CPU工作站,运行内存为128 G。

4 结果与分析

4.1 喷雾流场形状

计算结束后,最终对流量Q进行后续处理,取空间中的3个切面进行可视化等值面显示,最终得到的结果如图9所示。通过结果比较可知,流量分布的范围与扇形喷嘴的理论范围基本具有一致性,有扇形的长轴与短轴,符合预期。通过对图形的初步观察,发现其流量分布具有两侧流量增大的特性,与实验结果相符。

图9 喷雾流场形状

为了改善喷嘴雾场的分布均匀性,需要研究扇形喷嘴的参数对雾场均匀性的影响,下面从切槽角、切深、接口形状以及喷射压力方面探究扇形喷嘴参数的影响。

4.2 切槽角

选择30°、55°、80°的切槽角,分别计算流量在长轴的等值面与向下喷射35 mm处、在长轴方向上的流量分布,结果如图10所示。

钢筋的应力-应变关系采用弹塑性硬化的两折线模型，如图1所示。其中弹性模量Es=2.0×105 MPa、屈服强度fy、强化段应变长度Δεy及极限强度fu根据材性试验确定，泊松比为0.3。

图10 不同切槽角下雾场流量等值面分布云图与长轴流量分布曲线

根据流量分布可知,切槽夹角对于流量的分布具有较大影响,切槽角度越小,扇形喷射的范围越大,且由于孔径大小一定,其总流量变化幅度不大,喷射范围增大使得在大范围下的单位面积流量减小,同时两侧的峰值均有一定程度减小,对于雾化效果有一个优化的作用。但是通过改变切槽角度并没有使流量分布中左右2个峰值完全消失。由于范围变化的平均化效果,其峰值也会有一定的降低,80°切槽的喷嘴具有最大的峰值,其峰值甚至高于中心位置,若是范围过大,其流量变化的峰谷宽度会进一步增大,单位面积的流量降低,将导致喷洒的效果降低,同时可能使得两侧峰值与内部的差距更加明显。因此减小切槽角度能够在一定程度上降低两侧峰值的影响,提高流量分布的均匀性,但还是需要根据实际生产选择合适的切槽角。

4.3 切深

基于原始模型,分别将切深增加、减少,变化幅度为0.3 mm,分别计算流量在长轴的等值面与向下喷射35 mm处、在长轴方向上的流量分布,结果如图11所示。根据流量分布可知,切深的效果与切角的效果类似,都增加了喷射范围,然而增加切深也提高了中间的整体流量,因此虽然中心位置的容积图显示其流量分布为两侧多、中心少,但是最终的累计流量具有均匀性,从而使得雾场流量的过渡更加平缓,相较于减小切角对于提高均匀性更具有正面意义。

图11 不同切深下雾场流量等值面分布云图与长轴流量分布曲线

4.4 接口形状

基于原始模型,改变接口形状为径向上的长椭球与扁椭球,分别计算流量在长轴的等值面与向下喷射35 mm处、在长轴方向上的流量分布,结果如图12所示。

图12 不同接口形状下雾场流量等值面分布云图与长轴流量分布曲线

根据流量分布可知,接口形状对于流量的分布具有很大的影响。结合流量分布图与等值面图,基于球状接口,形状发生拉长,在长椭球的情形下会使两侧的峰值范围进一步增加,使不均匀度进一步增强,具体表现为在整体流量变化微小的情况下,中心部分的流量减少,这部分流量往两侧峰值部分靠拢,形成两侧流量更大,中心部分流量更小的流量分布。而对于球状接口形状发生压缩,在扁椭球的情况下会使两侧的峰值流量减少,具体表现为两侧的峰值流量在一定程度上以自身为中心向外偏移,使得整体的流量更加具有均匀性。

4.5 喷射压力

基于原始模型,改变喷射压力,选择0.15、0.3、0.5 MPa的喷射压力,分别计算流量在长轴的等值面与向下喷射35 mm处、在长轴方向上的流量分布,结果如图13所示。

图13 不同喷射压力下雾场流量等值面分布云图与长轴流量分布曲线

根据流量分布可知,不同压力条件对于雾场的散射角与流量分布影响不大,喷射压力对于整体的流量大小具有一定影响,且是一种正相关的线性关系;同时可以看到在等值面的末尾,雾场形状具有略微的偏折,压力越大则这种偏折效果越小,这是由重力加速度引起的偏折,因此压力越大,其流场的速度越大,受到重力加速度的影响越小。由此可知,雾场的喷射角度与喷射压力之间的关系是与重力加速度共同影响产生的,其本身并不会对雾场的角度造成影响。

4.6 仿真小结

通过对仿真瞬态计算的慢速观察,能够发现最终喷射的流量分布状态与液流最初从喷嘴口射出时的分布状态具有很大的关联。液流在喷射最开始时就已经展现出三峰分布的趋势,如图14所示,而喷射后的液膜扩散运动也只是放大了这种趋势。

图15 喷嘴口切口纵截面示意图

基于这种分析可以对喷嘴参数对于喷雾流场的影响进行总结:

1) 改变喷射压力对于喷射出口的液流分布没有影响,因此对出射时的流量分布没有影响,但是会影响出射时的速度。此时影响的是液膜的扩散性,若其扩散性能远小于重力或者张力,则喷雾的效果会大打折扣。

2) 改变槽切角会改变喷射时的液流对撞角度,从而影响其扩散性能,同时也改变了出射的孔径,因此减小槽切角,会增加扩散性能,减小整体的流量,中心与两侧的峰值都因扩散性能得到了缓解,从而在一定程度上增加了均匀度。但是奇异点并没有从根本上消失,因此仍然具有两侧的双峰。

3) 改变切深能够改变边缘奇异点的效果。与改变切角不同的是,增加切深会使得切口的整体变大,从而减小两端的奇异点效果。

4) 改变接口形状能够改变液流在喷嘴内部聚集的效果,从而改变出射后的流量分布。将接口形状变为扁椭球形会增大中心的扩散效果,同时减小切口两端的奇异点效果,最终使得整体的均匀性有一定程度的提升。

5 结论

仿真研究结果表明,扇形喷嘴雾场流量趋势具有3个峰值,喷雾流场的均匀性能差,不能满足高精度的生产要求。喷嘴的两侧峰值由切口与内径之间的偏差产生的液流奇异点导致的。喷嘴槽切角、喷嘴切深以及喷嘴接口形状都会对喷嘴喷雾流场的均匀性产生影响。槽切角主要影响液流的扩散性能,可通过增加扩散性能来改善喷嘴喷雾流场的均匀性。切深能够改善边缘的奇异点,从而改善喷雾流场的均匀性能。改变接口形状能够同时改善扩散性能与奇异点,从而改善喷嘴喷雾流场的的均匀性。针对扇形喷嘴流量均匀性的改善,需要综合考虑槽切角、切深以及接口形状,并且深入理解边缘奇异点与喷嘴的扩散性能对喷雾流场的均匀性的影响。研究结果表明基于扇形喷嘴实现均匀喷射具有可行性。