改进二进制麻雀搜索的特征选择及文本聚类
高新成,邵国铭,张海洋,周中雨
(1.东北石油大学 现代教育技术中心, 黑龙江 大庆 163318;2.东北石油大学 计算机与信息技术学院, 黑龙江 大庆 163318)
0 引言
文本聚类是一种无监督学习的文本挖掘技术,其目的是将距离相近的文本聚类到相同的目标簇中[1]。因此,文本聚类被广泛地应用到网页挖掘、垃圾邮件过滤、新闻文本聚类等领域[2]。矢量空间模型(vector space model,VSM)作为常用的文本表示模型,可以将文本构建成对应的词条权重向量,用以计算文本间的相似度。由此,文本聚类的效果受到特征维数以及特征子集冗余性等因素的影响[3]。文本特征包含有效特征和无效特征。其中,无效特征包含噪声或冗余特征。文本特征选择的目标是通过筛选无效特征选取最优特征子集,使文本聚类效果最佳。传统特征选择方法存在难以改进以及特征选择精度较低等问题。
本文中设计了一种结合蜣螂优化算法DBO[4]改进二进制麻雀搜索算法的特征选择及文本聚类算法。将麻雀的位置信息建模成文本特征,各麻雀的适应度值建模为特征子集的评价指标,引入蜣螂优化算法中圆周方向搜索机制改进麻雀发现者的位置更新策略,同时融合滚动方向机制的随机游走策略提升麻雀全局搜索能力,选取最优文本特征子集。在文本特征选择最优解的基础上,选用k-means++聚类算法,得到最优文本聚类结果。通过标准文本数据集及评价指标对比,最终验证算法的有效性和可行性。
1 相关研究
目前常用的特征选择方法主要有以下3种:过滤式(filter)、封装式(wrapper)和嵌入式(embedded)。其中,过滤式特征选择方法[5]未考虑与学习算法结合,本质上是一种数学统计分析法。封装式特征选择算法结合了学习算法,并利用相应的搜索策略选取最优特征子集。嵌入式方法将特征选择与学习算法结合成一体,在训练阶段已经完成了特征选择工作。
近年来,元启发式算法被广泛应用到各个领域以解决优化问题[6],包括医疗领域、环保领域及农业领域等。在文本挖掘领域中,Janani等[7]提出了基于粒子群算法的文本聚类算法,利用常见的文本数据集进行实验。许召召等[8]提出了融合信息增益比和遗传算法的混合特征选择算法,并利用信息增益比的过滤式算法进行特征初选,再利用遗传算法对特征进行优化。张阳等[9]提出了一种基于word2vec和高维生物基因选择遗传算法的文本特征选择算法。王琛等[10]将灰狼觅食的过程模拟成特征选择的过程,利用k-means算法完成文本聚类。Bae等[11]提出了一种基于和声搜索算法的特征选择方法,在聚类的准确率和精确率上有良好的效果。罗子淦[12]在二进制粒子群优化算法的基础上引入学习因子等改进策略,有效缩减了特征数量。
由此,使用元启发式算法可以有效地进行特征选择,而传统智能优化算法存在寻优能力不佳及收敛速度较慢等问题,即使与过滤式特征选择算法相结合,其提升效果也不是很明显。麻雀搜索算法[13]是一种新型智能优化算法,优点是收敛速度快,算法参数少且适用于求解大规模问题。研究表明,麻雀搜索算法的寻优能力优于PSO[14]、GA[15]和灰狼[16]等优化算法,已被广泛地应用在电力系统、图像处理及网络安全等领域。
虽然麻雀搜索算法(SSA)在多个优化问题上表现优秀,但在处理大规模离散优化问题,例如特性选择时,SSA存在一些明显的局限性。具体来说,由于SSA最初被设计用于处理连续问题,因此其在处理离散问题时,存在收敛速度较慢及寻优精度低的问题,有时可能陷入局部极值。此外,SSA的发现者位置更新公式具有较大的随机性,虽然在搜索初期有助于全局搜索并防止算法陷入局部最优,但在搜索的后期,这种随机性会阻碍算法进行更精细的局部搜索,进一步影响寻优精度和速度。针对这些局限性和挑战,本文结合蜣螂优化算法DBO,提出了改进的二进制麻雀搜索算法(IBSSA),旨在提升麻雀搜索算法在大规模离散问题上的寻优效率和精度。
2 算法详细设计
传统的麻雀搜索算法主要被用来解决连续型优化问题,而特征选择[17]是一种离散优化问题。本文将通过二进制麻雀搜索算法实现文本的特征选择,在去除冗余特征的最优子集基础上,进行文本聚类分析。算法主要分为3个阶段:第一阶段进行文本预处理及构建矢量空间模型VSM。第二阶段利用改进的二进制麻雀搜索算法进行文本特征选择,得到最优文本特征子集。第三阶段在最优文本特征子集基础上,利用k-means++实现文本聚类。
2.1 构建基于矢量空间模型VSM的文本表示模型
在进行文本特征选择之前,需要对文本进行预处理,将其表示为矢量空间模型VSM[18]。其中包括分词、去停用词、提取词干及计算词条权重。分词的主要操作是根据标点符号和空格,将初始文本分割成单独的词条。去停用词是将文本中出现频率较高但其权重值较小的词语进行移除,减少其对聚类结果的影响。提取词干操作是通过去除词汇的前缀与后缀并将词汇转换为相同词根的过程。其中,相同词根被定义为文本的同一个特征。词条权重计算是根据特征词条在不同文档中出现的频率,计算其对应的权重值。特征词条出现的频率越高,词条在文档中越重要,其拥有的权重值越大。目前常用的特征词条计算方法为词频-逆文档频率TF-IDF,具体公式如下。
wi, j=TF(i,j)×IDF(i,j)=

(1)
式中:wi, j为文档i中特征词条j的权重值;TF(i,j)为文档i中特征词条j出现的频率;n为文档总数;DF(j)为包含词条j的文档数量;IDF(i,j)为逆文档频率,最终构建矢量空间模型VSM。
2.2 基于二进制麻雀搜索算法的特征选择策略
麻雀搜索算法是受到麻雀捕食及反捕食的启发而提出的种群智能优化算法。它将麻雀的觅食过程抽象为拥有预警机制的麻雀发现者以及麻雀加入者模型。在每次迭代搜索前,算法通过计算适应度值的大小,将麻雀分为发现者和加入者。发现者为麻雀种群寻找食物来源,加入者跟随发现者寻找食物,发现者和加入者之间可以相互转换。在觅食过程中,部分麻雀被选作侦察者以及时发现危险。
2.2.1 特征选择模型
在机器学习与数据挖掘领域中,特征选择的目标是在保持原始特征较高准确性的前提下,选取样本的最优特征子集。假定初始文本特征集合为F,其可以表示为Fi={fi,1,fi,2,…,fi, j,…,fi,n},其中Fi为文档i的特征集合,n为特征数量。令FS为特征选择之后得到的最优特征子集,表示为:FSi={fsi,1,fsi,2,…,fsi, j,…,fsi,m},其中m为特征选择后新的特征长度,fsi, j={0,1},j=1,2,…,m。当fsi, j=1时,文档i中选取的特征j为有效特征;当fsi, j=0时,文档i中特征j为无效冗余特征。
2.2.2 解的表示
在使用二进制麻雀搜索算法进行文本特征选择时,每只麻雀在搜索空间中的位置代表一个文档的特征子集。将一只麻雀s的位置表示为矩阵Xs,则Xs可表示为:

(2)

2.2.3 适应度函数
元启发式算法的适应度函数主要是用来评估麻雀位置所代表的特征选择解的适应度值。特征词权重是衡量文本聚类的重要指标,权重越高的特征对聚类的影响越大。平均绝对差MAD可用于衡量文本特征子集的稳定性与一致性。本文从文本特征权重角度出发,通过计算麻雀所选特征子集上下文特征权重的平均绝对差MAD,将其作为特征选择的适应度函数,使其具备衡量文本特征价值的能力,其公式如下。

(3)

(4)

2.3 改进二进制麻雀搜索算法
传统的麻雀搜索算法SSA主要是用于解决连续型优化问题的元启发式算法,而文本特征选择是一种求解离散优化的问题。本节主要介绍麻雀搜索算法、离散化技术以及用于求解特征选择问题的改进麻雀搜索算法IBSSA。
2.3.1 二进制麻雀个体更新策略
传统麻雀搜索算法中的发现者指的是具有较高适应度值的一部分麻雀,其位置更新如式(5)所示。
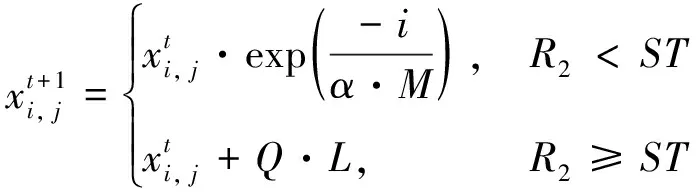
(5)
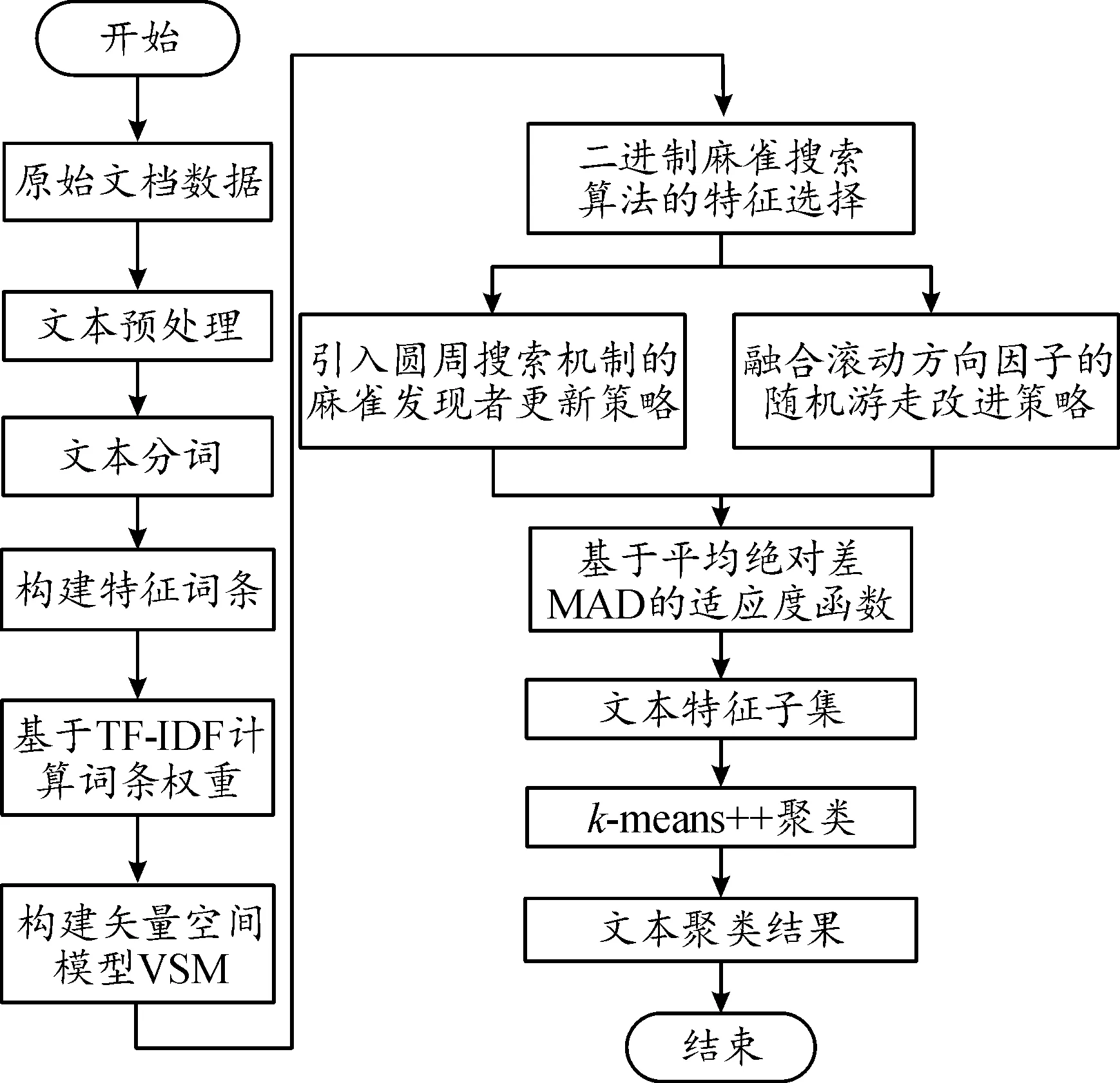
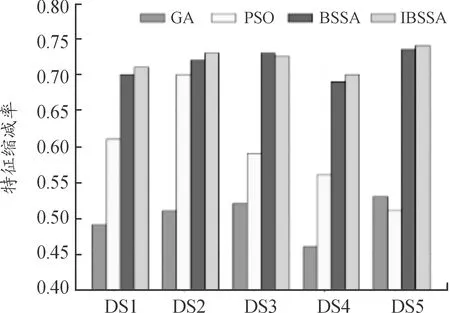
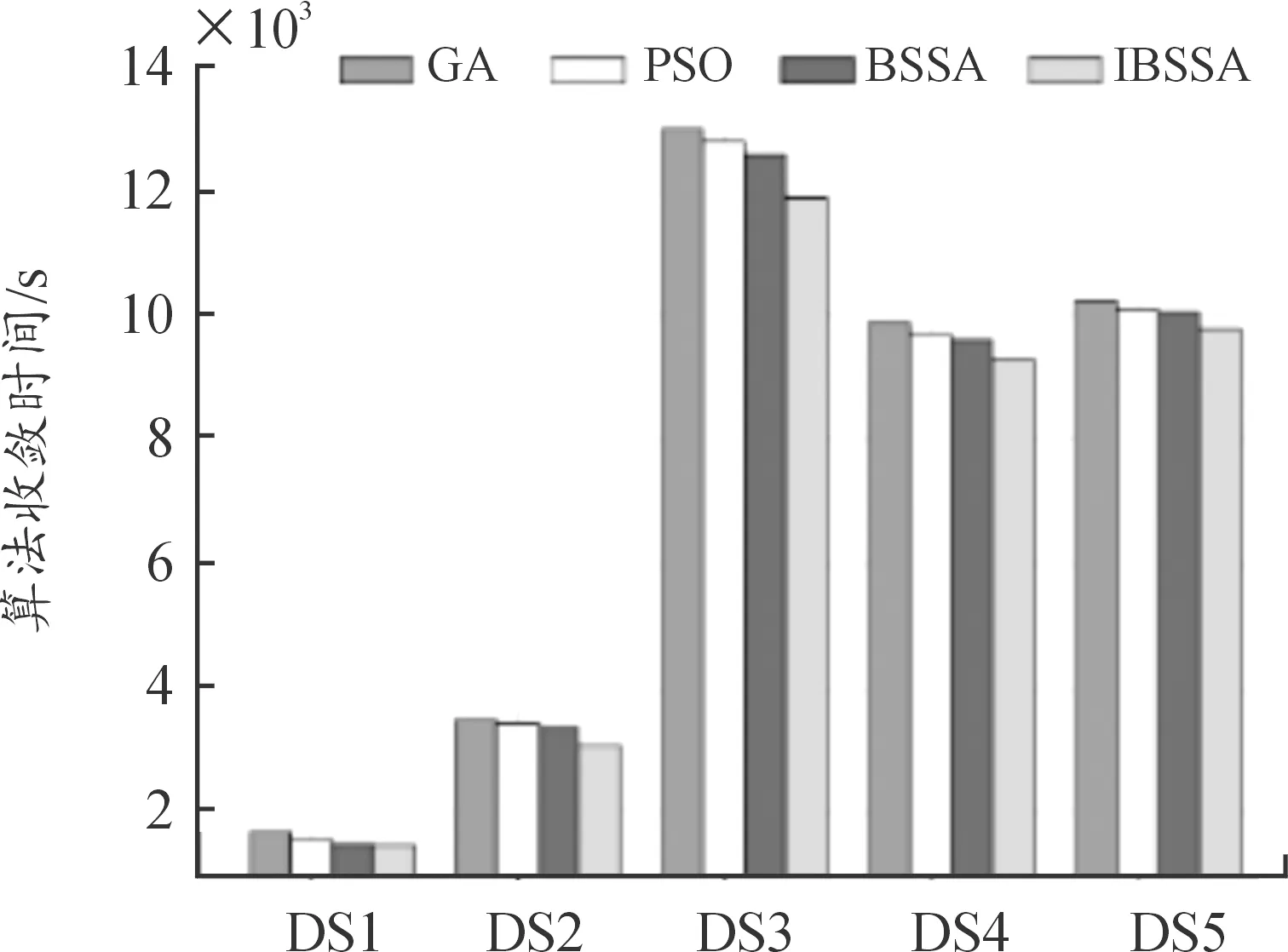
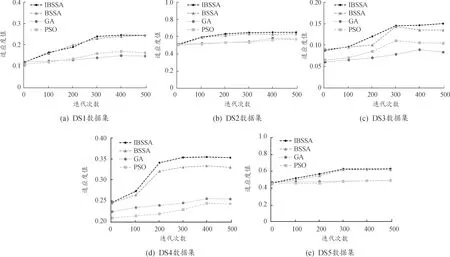
式中:xi, j为麻雀i在j维上的位置信息,1≤i≤N, 1≤j≤D;t为当前迭代次数;α∈(0,1];M为最大迭代次数;R2∈[0,1],表示麻雀的预警值;ST∈[0.5,1],表示麻雀的安全值;Q为服从标准正态分布的随机数;L为1×D的全1矩阵。当R2 传统麻雀发现者公式虽然简单易行,有助于跳出局部最优解,但是其在搜索空间中的移动缺乏方向性,随机移动虽然能避免局部最优,但其也可能使得算法在搜索过程中偏离全局最优区域,其移动距离Q·L也是随机的。算法可能在一次迭代中移动很大的距离,而在另一次迭代中只移动很小的距离。这种不稳定性可能会对算法的收敛性产生负面影响,且其移动主要基于当前位置和随机数,却忽略了过去的搜索历史。因此,它无法有效地利用过去的搜索经验来引导算法进一步搜索。 为了解决麻雀发现者在搜索空间中移动时缺乏方向性及移动距离不稳定的问题,引入一种基于圆周搜索的机制。通过结合蜣螂优化算法,圆周方向搜索机制对麻雀发现者进行改进后的位置更新策略如式(6)所示。 式中:r是圆周半径随机数,表示一个随机距离,取值范围为 (0,1);θ是一个随机角度,表示在一个单位圆上选择一个随机方向,取值范围为 (0,2π);[cos(θ),…,sin(θ)]为一个dim维的位移向量,dim对应特征选择解的维度。若R2 基于圆周搜索机制改进的麻雀发现者利用[cos(θ),…,sin(θ)]使得算法在搜索空间中的移动有一定的方向性,可以更好地控制搜索方向,避免算法过于随机地在搜索空间中移动。基于圆周搜索机制,引入圆周半径因子r可以更好地控制搜索距离,保证算法在每次迭代中的移动距离在一定范围内,提高算法的稳定性,更好地利用先前搜索经验引导搜索过程。 麻雀搜索算法中的加入者指的是具有较低适应度的大部分麻雀,其位置更新如式(7)所示。 (7) 麻雀警戒者主要由麻雀种群随机选取产生,一般选取15%左右的麻雀作为警戒者,其位置更新如式(8)所示。 (8) 转移函数TF是一种可以按一定概率将实数转换为0或1的方法。本文借鉴Agrawal等[19]提出的基于改进二进制优化算法的公式,将传统麻雀搜索算法改进为解决离散特征选择问题的二进制麻雀搜索算法,其公式如下。 (9) (10) 2.3.2 改进随机游走策略 当二进制麻雀搜索算法迭代进入停滞状态导致种群无法获取最优适应度值时,随机游走策略可以通过对二进制麻雀种群中最优麻雀个体的扰动,帮助算法跳出局部最优解。基于随机游走策略改进的最优麻雀个体的更新公式如式(11)所示。 (11) 算法:随机游走策略 1.PI#根据参数PI改变上下界ub、lb的范围,迭代次数越大,范围越小,用以调整搜索范围。 2.cur_iter #当前迭代的次数 3.Initial PI with cur_iter 4.lb=lb/PI 5.ub=ub/PI 6.forjin range (Dim):# Dim对应搜索的维数 7.ai, j:确定每一个维度的搜索下界 8.bi, j:确定每一个维度的搜索上界 11.生成一个步长A:[-1,1]之间 13.更新第j个维度的位置 14.{xmin,xmax}:[-1,1] 17.end if 18.end for 传统随机游走算法中,步长A的公式如下。 Aij=2*(Randij>0.5)-1 (12) 式中:Randij是在[0,1)间均匀分布的随机数。 传统随机游走算法步长的生成完全随机,没有考虑到搜索过程中的方向性,导致搜索过程可能过于单一,不能充分探索搜索空间。搜索结果可能在正负方向上来回振荡,效率较低。 本文中提出了一种改进的步长生成方法,即引入了一个滚动方向因子direction,用于决定搜索方向。步长A的改进公式为: Aij=direction*(2*(Randomij>0.5)-1) (13) 式中:direction是 {-1,1} 中随机选取的值。引入滚动方向机制后,算法搜索更有可能沿着某个方向进行,减少了在正负方向上的振荡。并且,由于滚动方向因子是随机选择的,搜索的全局性依然能得到保证,不会因为引入方向因子而导致搜索能力下降。 本节中提出了改进的二进制麻雀搜索算法(IBSSA)。首先,通过转移函数TF将传统麻雀搜索算法改进为解决特征选择问题的二进制麻雀搜索算法BSSA。其次,传统麻雀发现者存在缺乏方向性等问题,通过引入圆周搜索机制,使得算法在特征选择搜索空间中的移动具有一定的方向性,同时能够更好地控制搜索距离,提高算法的稳定性。再次,在二进制麻雀搜索算法基础上引入传统随机游走策略虽然在一定程度上有助于特征选择时跳出局部最优解,但其存在步长缺乏方向性等问题,通过引入滚动方向因子,可以使得搜索结果更有可能沿着某一方向进行,有利于算法减少正负方向震荡,提高搜索效率。 图1为改进二进制麻雀搜索的特征选择及文本聚类整体流程。该流程主要分为3个关键阶段:左侧为整体流程第一阶段,首先将原始文档数据进行预处理,包括清洗、标准化和分词等操作,然后构建特征词条并计算基于TF-IDF的词条权重,最后生成矢量空间模型(VSM)。该阶段为后续的特征选择和文本聚类建立了基础的数据表示。第二阶段,应用改进的二进制麻雀搜索算法进行特征选择。在传统的二进制麻雀搜索算法基础上,引入基于圆周搜索的麻雀发现者更新策略和融合滚动方向因子的随机游走改进策略以改善特征选择的效率和稳定性。此外,采用基于平均绝对差(MAD)的适应度函数对搜索过程进行引导,以确保寻找的特征子集能够最大化聚类性能。第三阶段,在寻找的最优特征子集基础上,利用k-means++算法进行文本聚类,得到最终聚类结果。 图1 特征选择及文本聚类流程框图 通过基准函数验证了结合蜣螂优化算法DBO改进的麻雀搜索算法的优化性能,并使用改进的二进制麻雀搜索算法IBSSA对文本数据进行特征选择,迭代寻找有效特征的最优特征子集。最终,使用k-means++算法对最优特征子集进行聚类,并通过计算多个评价指标,观察基于二进制麻雀搜索算法特征选择后的文本聚类结果性能。 为验证结合蜣螂优化算法DBO改进的麻雀搜索算法的优化性能,参考孙林等[20]的实验方法,选取6个基准函数,如式(14)—式(17)所示。其中,F1—F4为单峰函数。单峰函数可用于测试优化算法的局部搜索能力及收敛速度。F5—F6为多峰函数,对应式(18)—式(19),多峰函数可用于测试算法的全局搜索能力及跳出局部最优的能力。选取的基准函数分别对粒子群算法PSO、遗传算法GA、原始麻雀搜索算法SSA、基于传统随机游走策略的麻雀搜索算法RWSSA、融入滚动方向机制的随机游走策略、圆周方向搜索机制改进发现者的麻雀搜索算法RW-DBO-SSA 5种算法进行对比实验。为确保实验结果的公平性,所有优化算法的参数均保持一致,种群数为30、空间维度20、最大迭代次数100,所有算法均运行20次。实验环境为Windows 10、CPU Intel i7 和8 GB内存,算法使用python编写。 (14) (15) (16) (17) (18) (19) 式中:单峰函数F1—F4对应搜索空间输入范围为[-100,100],最优值为0。双峰函数F5对应搜索空间输入范围为[-5.12,5.12],F6对应搜索空间输入范围为[-32,32],最优值均为0。 图2展示了5种优化算法在6个基准函数上的收敛曲线,横坐标表示优化算法迭代次数,纵坐标为算法所对应的适应度值。 图2 不同算法在基准函数的收敛曲线 由图2(a)—图2(d)可知,求解本节中4种单峰函数时,RW_DBO_SSA算法的寻优精度及收敛速度优于其他4种优化算法。由图2(e)和图2(f)可知,在求解多峰函数问题时,RW_DBO_SSA算法相比其他4种优化算法具有更优的全局搜索能力及收敛性能。综上,结合蜣螂优化算法的滚动方向机制优化随机游走策略和圆周方向搜索机制改进麻雀发现者策略得到的改进麻雀搜索算法有较好的收敛速度及寻优能力。 采用表1所示的5种基准文本数据集进行实验,测试基于二进制麻雀搜索算法IBSSA的特征选择算法的性能。该算法是基于滚动方向机制的随机游走策略及圆周方向搜索机制改进发现者的麻雀搜索算法RW-DBO-SSA经转移函数TF转换所得,适用于解决特征选择问题。基准文本数据集由计算智能实验室LABIC提供。数据集包括:文本数量、文本特征数、聚类数。对比算法选择基于粒子群的特征选择及文本聚类算法PSO-FS和基于遗传算法的特征选择及文本聚类算法GA-FS,以及未使用任何文本特征选择方法的k-means++ 算法。 表1 测试文档数据集 采用准确率Accuracy(Acc)、查准率Precision(P)、查全率Recall(R)和F度量F-measure(F)作为评估聚类效果的方法。此外,为进一步验证基于二进制麻雀搜索的特征选择算法的性能,引入特征数量缩减率和适应度值收敛性2个指标。 1) 查准率P (20) 式中:ni, j为聚类j中属于分类i的成员数量;nj为聚类j的成员数量。 2) 查全率R (21) 式中:ni, j为聚类j中属于分类i的成员数量;ni为聚类i的成员数量。 3)F度量 F-measure可用于度量聚类结果的性能,其结果为查准率和查全率的调和平均值。 (22) 式中:P(i,j)为聚类j中分类i的查准率;R(i,j)为聚类j中分类i的查全率。所有聚类的F度量为: (23) 式中:n为文档总量。 4) 准确率 准确率Accuracy是用来计算真实文档被分为正确类别的比例,如式(24)所示。 (24) 式中:P(i,j)为聚类j中分类i的查准率;K为聚类总数;n为文档总数。 5) 特征数量 该评估指标表示基于改进二进制麻雀搜索算法后,得到的有效特征数量,特征的有效选取对于文本聚类的性能和准确度具有重要的影响。特征数量的优化和选择是一项关键指标。 6) 收敛性 该指标用来评估算法对有效特征的寻优能力及速度。 图3是5种测试数据集使用遗传算法、粒子群算法、二进制麻雀搜索算法以及改进的二进制麻雀搜索算法得到的特征缩减率的情况。其中,遗传算法的特征缩减率在45%~55%,相对较差。粒子群算法的特征缩减率在50%~65%,表现一般。二进制麻雀搜索算法的特征缩减率在65%~75%,表现较好。改进的二进制麻雀搜索算法的特征缩减率在70%~75%,相对其他3种算法,改进的二进制麻雀搜索算法可以更好地降低无效特征,说明改进的二进制麻雀搜索算法在求解特征选择问题上是有效可行的。 图3 特征缩减率 图4是4种优化算法在完成特征选择后的收敛时间,相比粒子群算法以及遗传算法,二进制麻雀搜索算法的收敛时间较短,迭代完成速度较快。改进的二进制麻雀算法的收敛时间优于传统二进制麻雀搜索算法,其迭代速度最优。 图4 算法收敛时间 图4也表明,在进行文本特征选择时,算法的运行时间与文本的特征数量及文档数量密切相关,文档数越多,特征数量也越多,算法进行特征选择的时间越长。 图5是5种测试文本数据集特征选择收敛性曲线,由式(3)计算适应度值,并通过若干次迭代,选取其最优适应度值。由图5可知,二进制麻雀搜索算法在迭代300次时收敛,较粒子群算法以及遗传算法收敛速度更快。改进的二进制麻雀搜索算法相比传统二进制麻雀算法有更好的适应度值,表明其更好的收敛速度及寻优能力。 图5 不同算法在5种数据集上的收敛性曲线 表2是4种优化算法在5种文本数据集上测试得到的聚类准确率、查准率、查全率和F度量值。其中,k-means++算法的聚类指标相对较低,主要原因是文本中存在大量无效冗余特征,k-means++算法没有使用任何特征选择机制。由PSO-FS及GA-FS的聚类结果可知,经过传统元启发式算法进行特征选择后,文本聚类的性能得到了提高。表2中, BSSA-FS相比传统优化算法,聚类性能得到进一步提升。IBSSA-FS在前4个文本数据集中,聚类性能最优,这表明改进的二进制麻雀搜索算法具有较好的寻优能力,可以有效地进行文本特征选择任务。 针对文本中存在无效冗余特征导致文本聚类性能较低等问题,提出了结合蜣螂优化算法改进二进制麻雀搜索算法的特征选择及文本聚类算法,引入了蜣螂优化算法中圆周方向搜索机制和滚动方向机制,对麻雀发现者位置及随机游走中步长公式进行改进。针对文本数据集,首先对其进行预处理,利用特征词权重作为目标函数,选取最优特征子集。对于麻雀搜索算法不能解决离散问题,结合转移函数对麻雀的位置进行更新,利用改进的二进制麻雀搜索算法进行文本特征选择。最终,改用k-means++聚类算法对选取的最优特征子集进行聚类。实验结果表明,提出的改进二进制麻雀搜索算法能够选取有效特征,较好地提高文本聚类的性能。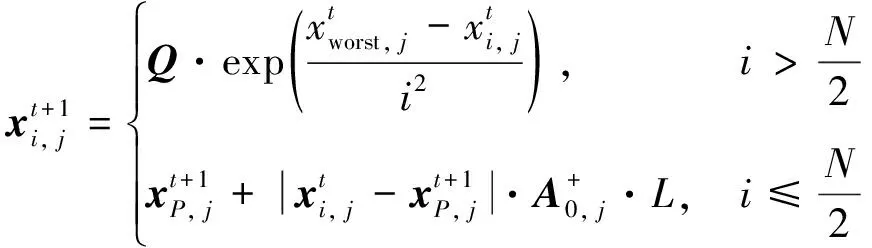






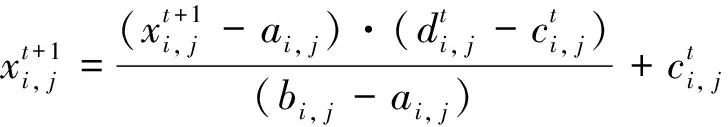


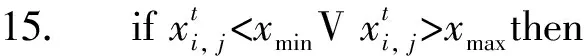
3 实验对比及分析
3.1 算法性能分析





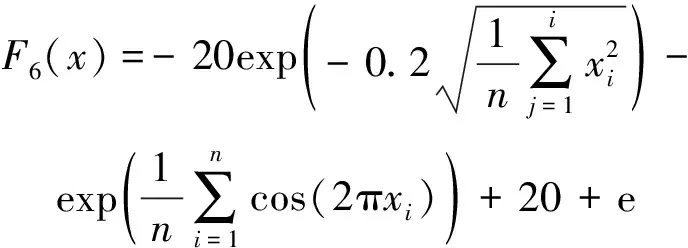

3.2 测试文本数据集

3.3 算法评估指标




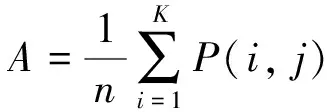
3.4 实验分析
4 结论

